三角形垂心的一个定理及其运用

洪海燕

定理 设ΔABC的垂心为H，外接圆半径为R，则AH=2RcosA，BH=2RcosB，CH=2RcosC．

当ΔABC为钝角三角形时，不妨设角A为钝角，如图2所示，易知AH=2Rcos（π－A）=－2RcosA，BH=2RcosB，CH=2RcosC．

当ΔABC为直角三角形时，不妨设角A=90°，如图3，可验证定理的结论仍然成立．所以定理对任意ΔABC都成立．

形式上与正弦定理类似．

以下略举数例说明定理的应用．

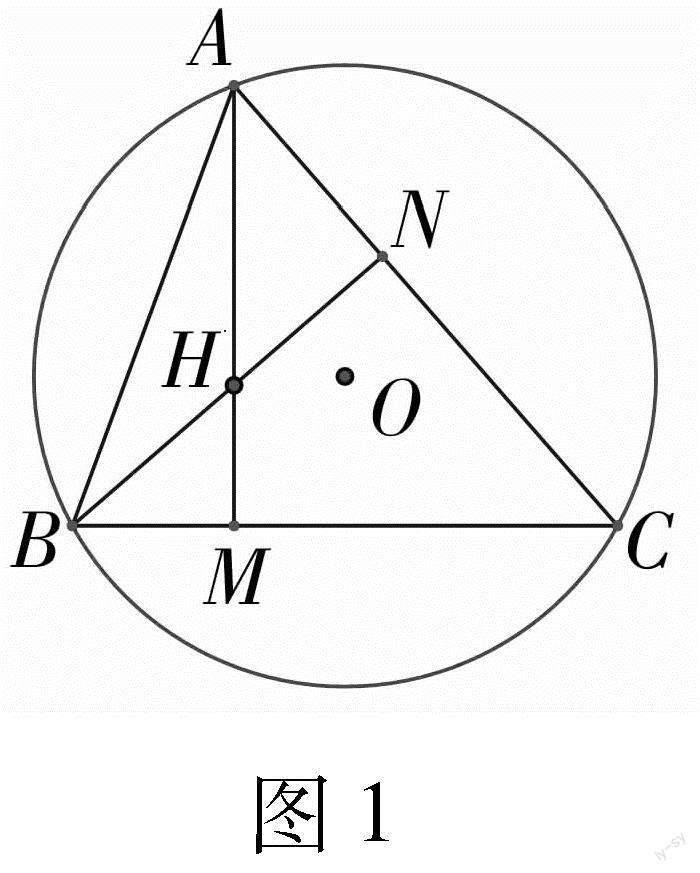
例2 （三角形垂心与外心之间的关系定理）三角形任意一个顶点到垂心的距离，等于外心到该顶点对边的距离的2倍．

证明：如图4，已知H，O分别是ΔABC的垂心和外心，OM⊥BC于M，ON⊥AC于N，OK⊥AB于K．即要证：AH=2OM，BH=2ON，CH=2OK．

同理有BH=2ON，CH=2OK．

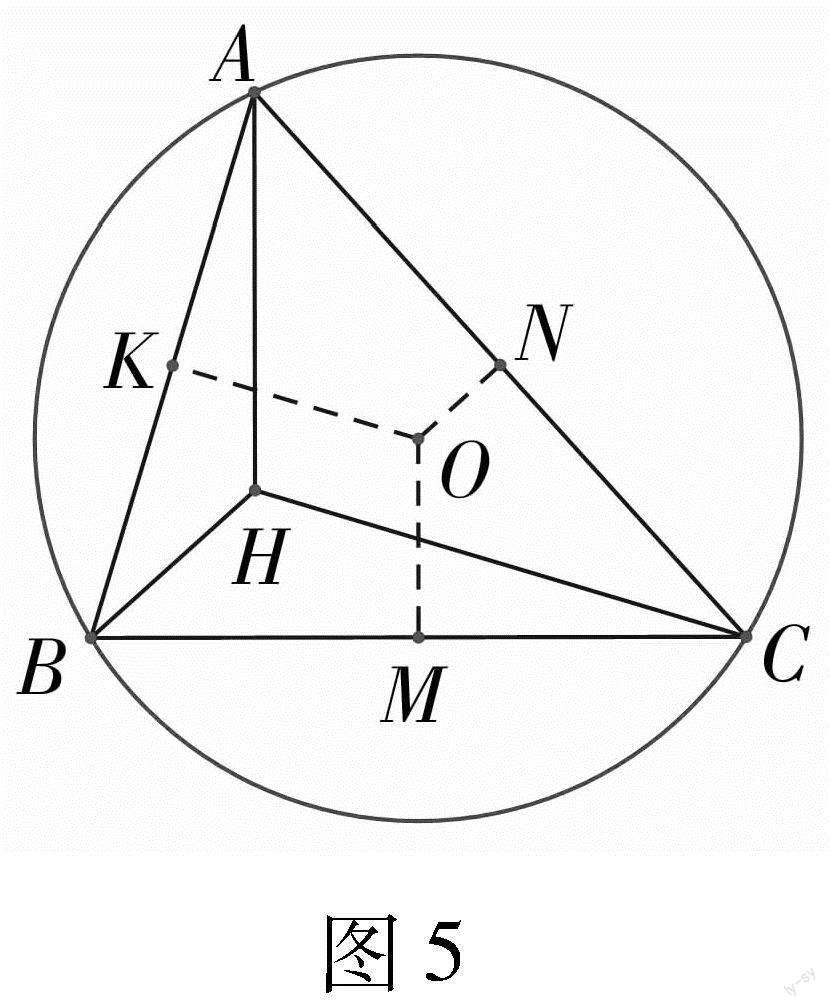
例3 设锐角ΔABC的外心与垂心分别为O，H，外接圆半径与内切圆半径分别为R，r，求证AH+BH+CH=2（R+r）．

证明： 如图5，过外心O分别作OM⊥BC于M，

ON⊥AC于N，OK⊥AB于K．由例2知AH+BH+CH=2（OM+ON+OK），

故以下只要證明OM+ON+OK=R+r即可．

再设ΔABC的面积为

OK aR=c·ON+b·OK ②.

由B，M，O，K四点共圆，同理有bR=a·OK+c·OM ③.

再由M，C，N，O四点共圆，有cR=b·OM+a·ON ④.

①+②+③+④得（a+b+c）r+（a+b+c）R=（a+b+c）（OM+ON+OK），

即R+r=OM+ON+OK．故所证命题成立．