基于学生立场的学习材料选择——以“带余除法”一课为例

浙江省金华师范学校附属小学 陈锋平

数学教学中的选材既要符合学生的年龄特点和思维现状，更要有利于学生对知识的理解感知和归纳提升。现笔者就“带余除法”不同的片段设计，做对比分析。

一、基于学生的想法准备学习材料

教学“带余除法”时，教师一般会从整除过渡到有余除法，下面两组材料是教学中教师经常选择的：

材料A:摆一个正方形用4 根小棒，8 根小棒可以摆几个这样的正方形？9 根呢？

材料B:把6 颗糖平均分在3 个盘子中，每盘里有几颗糖？把7 颗糖平均分在3 个盘子中呢？

乍一看这两组材料，似乎没有什么差别。但如果从学生思考的过程出发，两组材料的差别便出现了：材料A 用9 根同样的小棒拼正方形，学生的第一想法是拼了2 个正方形，但拼第3 个正方形还少3 根；教师引导学生用算式表示：9÷4=2（个）……1（根）。这组材料对学生来说是还少几根小棒而不是多了几根小棒。这里的余1 根是要从还少3 根转个弯回来的。教师让学生增加小棒根数继续拼，当用11 根小棒拼时，拼成了2 个正方形，但拼第3 个正方形还少1 根，列式为11÷4=2（个）……3（根），这时感觉就更明显了，需要把缺少3 根转化为剩余1 根。因此，通过这组材料的学习，学生感受更多的是“想到少了几根小棒，而不是多了几根小棒”。

如果让学生使用材料B，把7 颗糖平均分在3 个盘子中，每盘2 颗，还剩1 颗，7÷3=2（颗）……1（颗），学生的理解是分了6 颗糖后还多了1 颗，这1 颗自然就是多余的。材料A 和材料B 本质上的区别是体现少还是多的问题，教师在选材的时候应该基于学生的想法进行材料的选择和准备，才能帮助学生通过尝试、交流、比较、分析等活动自主去探索、去发现，建构新的知识结构。

二、贴近学生的感觉准备学习材料

下面继续对比分析分糖和装乒乓球两组材料。

材料A:把8 颗糖平均分在3 个盘子中，每盘里有几颗糖？把7 颗糖平均分在3 个盘子中呢？

材料B:有12 个乒乓球，每6 个装一盒，能装几盒？13 个乒乓球呢？14 个呢？……

如果选用材料A，当把8 颗糖等分到3 个盘子中时，列式8÷3=2（颗）……2（颗），每盘分到2 颗，余下也是2 颗，商和余数都是2，单位也一致，“余”的感觉不明显。如果选用材料B，当把14 个乒乓球每6 个装一盒，能装几盒？还余几个？列式14÷6=2（盒）……2（个），尽管商和余数都是2，但因为单位不一样，商是2 盒，余数是2 个，2 盒给学生的感觉就是“整的”，2 个给学生的感觉就是“余下”的。所以，“分糖”与“装乒乓球”对比，装乒乓球更利于学生感受到带余除法中商和余数的区别。

要想数学学习材料凸显“数学味”，教师应尽量选择贴近学生感觉的学习材料。通过对这样的学习材料展开思考和研究，数学学习过程就会变得更容易理解，数学学习也会变得更生动。

三、有利于学生的提炼准备材料

材料A:

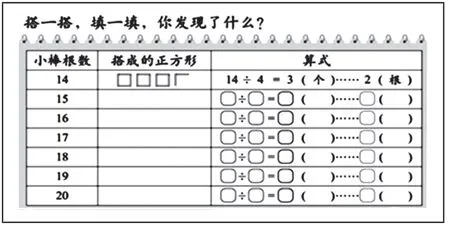
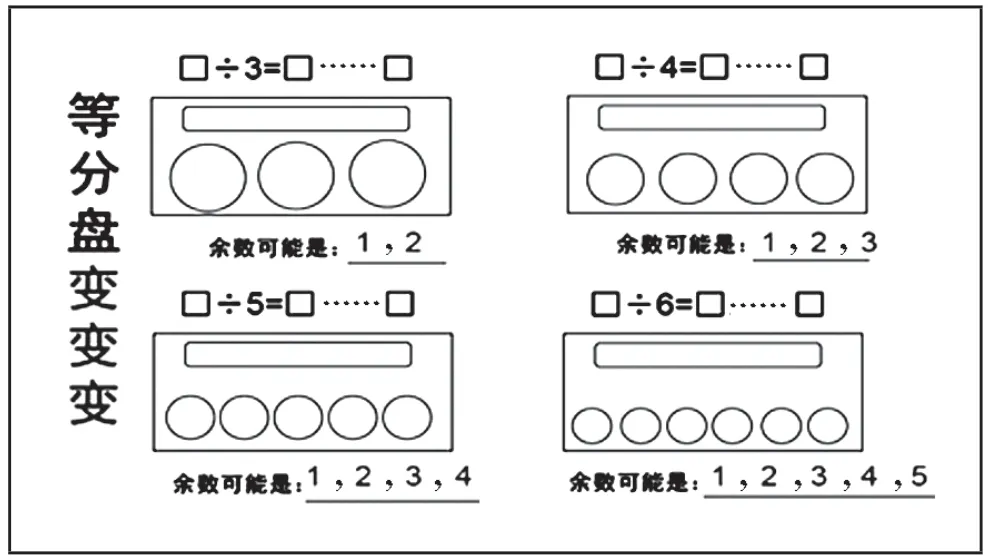
材料B:

材料A 用一组算式来研究余数的特点，会受两个因素的干扰，一是如果将呈现的算式逐一计算，需要花很多时间，如果不计算呢，学生心里又不踏实。如果再出现一组除数是4 的算式进行比较，计算量就更大了。二是通过观察算式，学生往往得到的是余数的变化规律，比如说平均分在3 个盘子中，余数会出现余1，2，0，1，2，0，…这一周期性的变化，很少有学生会把除数和余数进行对比。

材料B 没有具体的除法算式，也没有出现余数的周期变化了，算式中只出现一个除数，学生能更专注地观察和思考余数只是和除数相关。以分糖为例，当把一堆糖平均分在3 个盘子中时，可能余下的是几颗呢？学生根据生活常识很容易明白不可能余下3 颗及以上的，因为还能再分。这时教师可以追问：如果把一堆糖平均分在4 个盘子中时，可能余下的是几颗呢？平分在10 个盘子中呢？……这样学生很容易明白余数一定比除数小，而不会把注意力放在余数的变化规律上。因此，是用算式组“找规律”，还是通过“等分盘变变变”来思考，哪个材料更有利于学生概括总结出“余数一定比除数小”，我们就选哪个材料。

数学是思维的体操。在选择学习材料的时候，教师应以学生的思维为突破口，用富有思考价值的问题和富有积极意义的操作，激活、发展学生的思维，使学生通过尝试、交流、比较、分析等活动自主去探索、去发现，建构新的知识结构。

四、为学生更能明白准备材料

下面两组关于分糖的材料只有细微的差别，材料A 的算式中，商和余数写上了单位，材料B 中的没有写，但它们在对帮助学生的理解方面却差别很大。

材料A:

12÷3=4（人）

13÷3=4（人）……1（块）

14÷3=4（人）……2（块）

15÷3=5（人）

16÷3=5（人）……1（块）

17÷3=5（人）……2（块）

18÷3=6（人）

19÷3=6（人）……1（块）

20÷3=6（人）……2（块）

21÷3=7（人）

（1）提问：观察算式，有什么发现？

（2）追问：为什么余数是1 或2？有可能是3 吗？

材料B:

12÷3=4

13÷3=4……1

14÷3=4……2

15÷3=5

16÷3=5……1

17÷3=5……2

18÷3=6

19÷3=6……1

20÷3=6……2

21÷3=7

（1）提问：观察算式，有什么发现？

（2）追问：为什么余数是1 或2？有可能是3 吗？

上面两份材料是同一位教师在说课和上课时的不同处理，如果直接省略商和余数的单位，看起来似乎简洁了，但其实不利于学生理解余数的意义。材料A 中13 块糖，每人分3 块，可以分给几个人？还剩余几块？列式为13÷3=4（人）……1（块），分给4 个“人”，余下1“块”糖，所以选择更能让学生明白的材料很重要。

数学教学中所选的材料要凸显数学学科知识的本质。所选的学习材料与教学目标要有针对性，教师在教学过程中要充分挖掘每个材料的价值及它们之间的关联，从而让学生真正把握教学内容的数学实质。