“正本促思”:指向素养提升的计算教学的应有路径
2024-04-04江苏省无锡市荡口实验小学
江苏省无锡市荡口实验小学 华 铠
计算教学在小学数学教学中占据着重要地位,对培养学生良好的学习习惯、提升其运算能力、发展其数学思维都起着积极作用。然而,在很多教师眼里,计算有规定的法则和顺序,有统一的格式和要求,简单的不需要讲,复杂的又讲不清,于是少讲多练、以练代讲的教学行为长期占据着计算课堂。在这样的课堂上,学生或许能习得熟练的计算技能,但能得到多少思维的发展、能力的锻炼呢?在着力培育学生核心素养的今天,如何改变计算教学“重技能习得,轻思维发展”的现状呢?“正本促思”是指向素养提升的计算教学的应有路径。
一、正儿童之本,按需教学,促思维走向有序
“算理”与“算法”是计算教学中的两大主角。以知识逻辑论,算理是算法的依据,没有算理,算法就是无根之木,理当先教算理再教算法;以认知特点论,算法易于掌握,算理难于内化,由易到难,理当先教算法再教算理。那么,“算法”和“算理”二者到底该谁先谁后呢?走近学习的主体——儿童,认识儿童真正的起点,发现儿童真实的需求,坚持以儿童为本,一切从儿童的需要出发,按需教学,有序教学,才能引领学生的思维走向有序。
(一)算理先行,循理入法
算理是客观存在的规律,算法则是人为规定的操作程序,当这种人为规定的操作程序对学生来说是全然陌生的、凭借经验完全无法推演时,先教学算法就如建造空中楼阁,显然是行不通的。这时,教师就应该搭好“算理”这个脚手架,这样,学生才能在理解算理的过程中提炼算法,完成自主构建。
例如,“两位数乘两位数的笔算”是乘法计算中的难点。没有超前的学习,对于竖式这种前人高度概括总结出来的方法,学生光凭短暂思考是很难理解的。然而,尽管“两位数乘两位数”对学生来说是一个全新的跨越,但是,当我们追根溯源剖析其本质时,就会发现学生对它的算理其实毫不陌生,即拆分成“两位数乘一位数”和“两位数乘整十数”。因此,以旧引新,催生转化思想的内需,先弄懂算理就成了这节课的前奏。有了算理的铺垫,算法自然水到渠成。
(二)算法先行,循法追理
理解算理固然是得出算法的必经之路,然而,当学生能够独立地从旧有的知识经验中自主迁移延伸,顺利掌握新的算法时,他们还有必要倒退回去先理解算理再推理算法吗?显然,顺应学生的天性,先尝试算法,让学生感受不教而会的成功感,再循着算法深究背后的算理以此来验证算法的正确性更合理。
例如,“三位数乘两位数的笔算”的教学片段如下。
情境:李叔叔想从某城市乘大巴车去上海需要12小时,大巴车每小时行80 千米;王叔叔想从某城市乘火车去上海也需要12 小时,火车每小时行120 千米。
师:阅读以上信息,你能提出什么数学问题?
生1:李叔叔所在的城市到上海一共多少千米?
生2:王叔叔所在的城市到上海一共多少千米?
师:解决这两个问题该怎样列式?为什么用乘法?
生:“80×12”“120×12”,都是“路程= 速度×时间”。
师:这两个乘法算式会计算吗?选一个试着算一算吧!
学生板书:
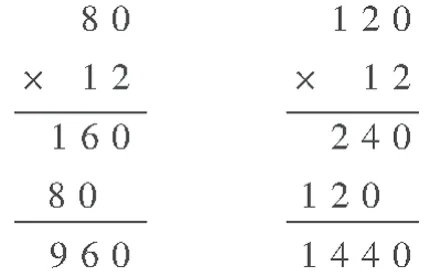
师:“两位数乘两位数”我们已经学过了,可“三位数乘两位数”老师还没有教,同学们怎么都这么厉害已经会算并还能算正确了?
生:这道题可以和“两位数乘两位数”一样,都是先用个位的数乘第一个乘数,再用十位的数乘第一个乘数,最后再把它们的积加起来。
师:这种能够借助旧知识和经验探究新知识的方法在数学中叫“迁移”,你们真聪明。
有了“两位数乘两位数”的笔算经验,学生完全可以自觉地完成类推。因此,教师创设真实情境引导学生自主提问、自主计算解决,放手让学生自主探索“三位数乘两位数”的算法,待学生顺利完成算法的迁移之后,再追问“为什么这个新知不学就能算”。巧妙的提问不仅帮助学生进一步掌握算法,还厘清了“两位数乘两位数”“三位数乘两位数”背后共同的算理。
二、正学科之本,深度教学,促思维走向深刻
许多计算课堂,有热热闹闹的计算,却没有安安静静的思考,在对计算结果和速度的过分追求中,数学被浅表化了。计算是数学,但是,数学不只是计算。张奠宙教授说过,数学的本质是数学知识的内在联系、数学规律的形成过程,是数学思想方法的提炼、数学理性精神的体验。小学数学的计算内容虽然基础、简单,但背后同样蕴藏着丰富而深刻的数学方法、数学思想和数学精神。教师只有坚守学科之本,设计能触摸数学内涵、感悟数学本质的深度教学,才能引领学生的思维走向深刻。
(一)操作启思,突破难点
例如, “两位数乘两位数的笔算”的教学片段如下。
情境: 计算能解决我们生活中的很多问题,比如,你能算一算这个电影院一共有多少个座位吗?(出示点子图,图略)
师:如果一个点表示一个座位,一排有28 个座位,有12 排,一共有多少个座位呢?要求全部的座位,也就是求12 个28 是多少,你会利用点子图先分一分,再列算式计算吗?
生1:我是这样分的,先算28×6=168,再算168×2=336。
生2: 我这样分,先算28×8=224,再算28×4=112,最后算224+112=336。
生3:我这样分,先算28×10=280,再算28×2=56,最后算280+56=336。
生4:我这样分,先算20×12=240,再算8×12=96,最后算240+96=336。
……
师:同学们通过分点子图找到了这么多种不同的计算方法,这些各不一样的方法有没有什么共同的地方?
生:它们都是先分再合。
师:为什么先要分?先分的好处是什么?
生: 先分可以把还没学过的“两位数乘两位数”变成学过的“两位数乘一位数或两位数乘整十数”,这样,对于没学过的乘法,我们也能算出来了。
师:是啊,分的过程也就是把新知转化成旧知的过程。刚才我们借助点子图,分三步求出一共有336 个座位,那你们能不能用竖式把这三步过程清楚地表示出来呢?来,试试看。
师:能说说你们都是怎么想的吗?比较这三种方法,你有什么想说的?
……
“两位数乘两位数的笔算”教学的难点是引导学生理解竖式中两个部分积的意义,也就是对基于乘法分配律的算理的理解。教师运用点子图,从最基本的乘法意义着手,让学生动手操作,分一分、算一算,使抽象的乘法算式在直观的图示上获得清晰的解释。在此基础上,教师再引导学生想一想、说一说“这些不同的方法之间有什么共同的地方”,最后让学生将操作的过程用竖式表达出来。精心设计的深度教学在学生畏难处“浓墨重彩”,使学生在轻松的做与思中,自动解锁难点,自然体会方法,使学习走向深处。
(二)对话导思,追根溯本
例如,“两位数除以一位数”的教学片段如下。
师:我们已经会用口算的方法和摆小棒的方法计算“46÷2”了,下面你能自己尝试用竖式来计算吗?
师:(指生1 的竖式)“46÷2”明明是一个除法算式,为什么这个同学写了两个除法竖式?你明白他是怎样想的吗?
生:因为“46÷2”要先算“40÷2”,再算“6÷2”,所以,他列了两个除法竖式。
师:真不错,用两个除法竖式能清楚地表达“46÷2”要分2 次计算。那如果要分3 次,要列几个竖式?(3 个)分4 次,5 次,6 次,更多次呢?
生:太麻烦了!
师:(指生2 的竖式)这个同学倒是一点不麻烦,一个这么简单的竖式就把结果计算出来了,只是——
生:感觉太简单了,这个竖式都不能看出要分2 次。
师:有道理!有没有办法只用一个竖式就能把分2 次的过程表达得很清楚呢?
师:(指生3 的竖式)这个同学和数学家的做法不谋而合呢!从这个竖式中,你能看出计算“46÷2”时先算什么,再算什么吗?
……
数学知识可以分为显性知识和隐性知识。“46÷2”该怎样列竖式,这是程序性的显性知识,易于传授;而“46÷2”的竖式本质就是口算中两次平均分过程的表达,这是隐性知识,难于把握。教师要用智慧解读学生的作品、学生的心理,用智慧创设有丰富对话空间的场域。通过不断交流、质疑、探讨、思考,学生主动取长补短,促使自己打破固有观念,知其然并知其所以然。精心设计的深度教学追根溯本,让隐性知识得以显现、内化,让学生的思维走向深入。
(三)联结拓思,融会贯通
例如,“两位数乘两位数”的教学片段如下。

课本原题 改编后题
师:不计算,你能很快判断出这个计算结果是否正确吗?
生:不正确!
师:这么快就确定结果是错误的,你的理由是什么?
生:我看积的最后一位,“1×3”结果应该是3,所以它错了。
师:真不错,用上了尾数判定法。大家还有不一样的想法吗?
生1:我是估算的,“120×10”结果是1200,结果应该比1200 大,所以是错的。
生2:三位数乘两位数,积最少也应该是四位数,因为最小的三位数100 乘最小的两位数10 结果也是1000 呢!
师:猜一猜,造成错误的原因是什么?
……
课本的原题是一道普通的改错题,旨在让学生在专项练习中进一步明确单一知识点“用十位上的数去乘,积的末位应该在十位上”。教师巧妙地把错题的中间过程隐藏了起来,并精心设计提问:“不计算,你能很快判断出这个计算结果是否正确吗?你的理由是什么?”原本简简单单的一道题融合了估算、巧算、笔算等知识点,留给学生的思考空间更大了,学生的推理能力、问题解决能力等也由此得到了提升。
计算课绝不应该就计算论计算,而应以学科能力的生长为目标,强调让数学知识真正在学生的心灵深处得以融会贯通。
(四)整理反思,迁移内化
例如,“三位数乘两位数”的教学片段如下。
师:同学们,三年级我们一起学习了“两位数乘两位数”,四年级我们学习了“三位数乘两位数”,猜一猜五年级、六年级我们又会学什么乘法呢?
生:五年级我们学“四位数乘两位数”,六年级我们学“五位数乘两位数”。
师:是这样吗?遗憾地告诉大家,五年级、六年级甚至初中,我们都不会再学习几位数乘几位数的乘法了,想一想,为什么就不学习下去了呢?
生:太麻烦了,生活中又不用。
师:哦,位数多了,乘起来确实有点麻烦呢,但生活中有时也会碰到三位数乘三位数的乘法,比如“123×456”,那不学又不用计算器的话,是不是就不会算了?
生:“三位数乘三位数”,我们也会算的,方法是一样的,先算“123×6”,再算“123×50”,然后算“123×400”,最后合起来。
师:那四位数乘四位数、八位数乘九位数……你们会算吗?
生:会!方法和道理都是一样的。
弗赖登塔尔认为,反思是数学思维活动的核心和动力。深度课堂是基于反思的课堂,经历了对知识的深度探究后,教师一定要及时引导学生反思和感悟。“为什么不学下去了?”“不学是不是就不会算了?”富有挑战性且直抵核心的问题引导学生对自己的认知重新认知,对自己的思考重新思考,使知识进一步得以拓展迁移,使学生进一步深化理解,内化感悟、完善认知结构、提升数学能力。
三、正发展之本,综合实践,促思维走向开放
随着科技的进步,要得到正确的计算结果,只需在计算器上按下数字和运算符号就能轻松获取,甚至更复杂、更高级的计算也有超级计算机可以帮忙。那么,为什么我们还要花费时间教学生学计算?一切为了学生的发展。在计算教学中,教师不仅要发展学生的计算能力,还要发展学生“会用数学的眼光观察现实世界”“会用数学的思维思考现实世界”“会用数学的语言表达现实世界”的能力。因此,在常规的课本计算教学之外,坚定发展之本,开展更综合性的主题学习、项目学习成为必然。例如,在学习了基本的整数计算之后,教师可以设计“三日周边短途游的方案预算”“家里卫生间翻新的预算”等实践活动;在学习了小数计算之后,设计“数说浪费小调查”“我家一周伙食小调查”等实践活动……丰富多彩的综合实践活动将数学与现实世界紧密相连,在解决真实问题的过程中,使学生的思维走向开放。
总之,有价值的数学计算教学,给予学生的影响应该是多元而立体的,既要有知识的丰厚、技能的纯熟,也要有方法的领悟、思想的启迪、精神的熏陶、能力的锻炼。事实上,立足“正本促思”的数学计算课的确拥有这一切,而且也可能传递这一切。
