经历规则形成过程 发展数学应用意识
2024-03-31邵汉民李建涛
邵汉民 李建涛


【摘 要】《近似数》是浙教版教材四年级上册“万以上的数”单元中的教学内容。教学中,教师要让学生结合具体情境理解近似数的含义,并经历四舍五入法的形成过程,学会用四舍五入法求万以上的数的近似数,最后通过题组比较,认识到“求近似数”与“改写”“单位换算”以及“进一法”“去尾法”的相同点和不同点。
【关键词】近似数;四舍五入法;准确数
《近似数》是浙教版教材四年级上册“万以上的数”单元中的教学内容,编排在《十进制计数法》《万以上数的读法》《万以上数的写法》的教学内容之后。在本课教学之前,学生已在二年级下册《加减法估算》一课中,学习了估算时取三位数的近似数和用“≈”表示估算的过程。从学生的生活经验来看,他们对近似数已经有了一定的感知,初步了解了用“大约”“左右”等表示近似数的方法。那么,在本课的教学中,如何利用学生已有的知识经验,帮助学生判断准确数与近似数?如何引导学生经历四舍五入法的形成过程?如何通过题组比较,加深学生对求近似数含义的理解?基于上述思考,笔者进行了如下教学实践。
一、创设情境,判断准确数与近似数
教师通过创设情境,让学生利用已有的知识经验和现实情境辨析准确数与近似数,初步感知近似数的含义,并通过对数学信息的比较,感悟到生活中许多人们以为的准确数,也可能是近似数。
(一)创设情境,发现差异
教师出示图1,让学生观察后,说一说图中讲了什么事,有哪些数学信息。学生指出,是张阿姨和李阿姨在交流张阿姨本月走的步数。张阿姨说:我本月走了十八万二千零六十八步。李阿姨说:你本月走了大约十八万步。
学生口答后,教师根据学生的回答板书(张阿姨:182068 18万),并提问:“为什么同一个信息有两种不同的说法?”学生利用原有的学习经验和现实情境,指出左边的数是准确数,右边的数是近似数(如图2)。接着,教师引导学生采用从左往右读与从右往左读两种不同的读法读一读,体会“约等号”左边是准确数,右边是近似数,因此不能从右往左读。
(二)进行质疑,体会含义
学生在现实情境中辨认了准确数和近似数后,教师质疑:“张阿姨已经读出了准确的步数,为什么李阿姨还要把它说成近似数呢?”学生讨论后认为,在这里取近似数可以方便记忆与书写。
教师接着出示数线图,在数线图上标注出17万、18万和19万的位置,进一步质疑:“近似数为什么不是17万或19万呢?”学生指出,因为“182068”更接近“18万”,所以它的近似数是18万。
(三)再认信息,提升量感
教师引导学生反思:“张阿姨说的真的是准确数吗?”学生结合生活经验进行思考,认识到这个数只是手机记录的“准确数”,张阿姨实际上走的步数可能比手机记录的步数要多(如张阿姨手机没有带在身边时走的步数就没有记录)。学生经历这样的说理过程后,教师指名学生报出自己的身高和体重,想一想它们是准确数还是近似数。学生认为,表示身高和体重的数虽然是近似数,存在误差,但这些数都可以表示自己当下的身高和体重。
“万以上的数”取近似数,其目的是在特定的情境下方便记录,同时能让学生通过对现实情境中具体数的反思,感受到人们所说的“准确数”是相对的,在一定的条件下也可能是近似数。通过这样的活动,学生更容易理解数的实际意义,发展数感和量感。
二、组织思辨,归纳四舍五入法
在学生理解了准确数与近似数的不同点后,如何引导学生掌握求近似数的方法?对此,教师可采用举例子的方法,让学生通过不断思辨、完善,归纳出四舍五入法。
(一)提出问题,引发思考
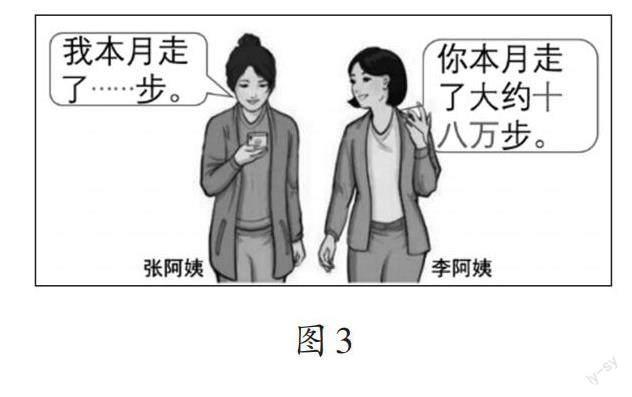
在认识到张阿姨手机上显示的步数也是近似数之后,学生意识到生活中很多看似“精确的数”也可能是近似数。准确数是有条件的,只有从手机显示来看,张阿姨本月走的182068步才是一个精确数。教师将图1的情境图改为图3,并让学生说一说有什么变化。学生发现,图3中没有了张阿姨本月走的具体步数。教师顺势提问:“张阿姨的手机上显示多少步时,可以说张阿姨大约走了18万步?”请学生举例说明。
(二)组织思辨,归纳方法
教师组织学生反馈各自所举的例子,学生感受到大家所举的例子之间有一定的联系。于是,教师进一步引导学生围绕准确数“182068”进行探究活动。教师先盖住个位,将其变成“18206□”,提问:“它的近似数是‘18万吗?”再在此基础上盖住十位、百位,并追问:“它的近似数还是‘18万吗?”在学生表示肯定后,教师再把千位也盖住,将其变成“18□□□□”,进一步追问:“它的近似数还是‘18万吗?”有学生认为不一定,如果千位上是“9”就不行了。
故教师引导学生思考:“要使近似数是‘18万,千位上还可以是什么数字?”学生指出还可以是4、3、1和0,教师顺势呈现184□□□、183□□□、181□□□和180□□□。接着,有学生提出,如果千位、万位都可以变,那这个数还可以变成175□□□、176□□□、178□□□和179□□□(如图4)。教师追问:“你们发现了什么?”学生討论、交流后发现:在图4右边一列,当千位上是“4”时,这个数最大,为“184999”。而在图4左边一列,当千位上是“5”时,这个数最小,为“175000”。
于是教师组织学生讨论175000这个特殊的数。175000正好是在17万与18万之间的中间数。教师向学生解释,数学上规定,中间数往大的方向取近似数,也就是175000≈18万,185000≈19万,启发学生感悟数学的和谐之美。
教师提问:“近似数是18万的这些数有什么规律?”教师根据学生的回答,概括出四舍五入法的含义,乃至四舍五入法求近似数的一般方法:一找(找省略尾数的最高位)、二取(用四舍五入法省略尾数)、三添(添上新的计数单位)(如图5)。
(三)练习巩固,形成技能
学生经历了四舍五入法的形成过程后,教师需要设计一些基础练习和变式练习,帮助学生把这一方法转变为熟练的技能。
教师出示下面两组练习。
1.把下面的同一个数分别省略“万”和“亿”后面的尾数,用四舍五入法求近似数。
235676000≈( )万 235676000≈( )亿
2.在下面的□里填上合适的数。
87□6000000≈87亿 87□6000000≈88亿
让学生先独立完成,再全班反馈和评析。反馈第1题后,引导学生进行比较,说一说求这两个近似数时有什么相同与不同点。学生发现:相同点是都用的“一找、二取、三添”的方法。不同点是,省略“万”后面的尾数求近似数时,尾数的最高位是“千位”;而省略“亿”后面的尾数求近似数時,尾数的最高位是“千万位”。第2题是教材中的练习,让学生完成后,说一说为什么要做这一道题目,并引导学生反思:用四舍五入法求近似数时要看尾数最高位上的数。
总之,教学时,教师不是简单地向学生告知四舍五入法,而要把四舍五入法作为探索规则的过程,让学生体会到:总结数学方法时,既要符合一般的规律,也需要进行规定。如“175000”处于17万与18万的中间,当把它纳入“五入”法时,“185000”也要纳入“五入”法。
三、题组比较,感受多元取整
在掌握了用四舍五入法求近似数后,可以结合题组,与改写、单位换算、进一法、去尾法进行比较,从而感受到四舍五入法只是取整的方法之一。
(一)比较改写与近似数
改写与求近似数都是用“万”或“亿”作单位,但它们的本质不同:数的改写是改变计数单位,却不改变数的大小;近似数则是既改变计数单位,又改变数的大小。教师可以通过如下题组,帮助学生辨析两者的联系与区别。
下面两个式子的左边部分是由9张数字卡片组成的九位数。只要知道哪些卡片上的数,就可以使式子成立?请在这些卡片上写上合适的数字。
让学生独立完成后校对,再比一比这两题有什么联系与区别。学生发现:第(1)题是改写,与原来的数大小相等;第(2)题是求近似数,填写时要看省略尾数的最高位是“四舍”还是“五入”。
(二)比较求近似数与单位换算
用四舍五入法求近似数与“单位换算”求近似数有相同的地方,两者都需要对原数的单位进行变换,但前者是变换计数单位,后者是变换计量单位。教师可以通过如下题组引导学生进行辨析。
按要求写出近似数。
(1)698115≈( )万
(2)698115平方厘米≈( )平方米
先让学生独立完成,再引导学生说一说各用怎样的方法求近似数。学生结合数位顺序表,发现数位顺序表中的“个位”与“万位”对应计量单位的“平方厘米”和“平方米”(如表1),从而感受到两者的联系与区别。
(三)比较四舍五入法与进一法、去尾法
近似数是指与准确数相近的数,除了用四舍五入法求近似数,还可以用进一法和去尾法求近似数。究竟用哪一种方法,需要根据实际情境来确定。教师可以通过如下题目引导学生比较这几种方法。
(1)货运码头要选择一艘货轮运货,货物总质量是203900吨。选择运货量是( )万吨的货轮运这批货物最合适。
A.20 B.21 C.22 D.23
(2)从甲码头到乙码头的运费是每万吨30万元,付600万元运费够吗?
先让学生完成第(1)题,说一说为什么要选择答案B。学生指出,如果用四舍五入法求近似数,大约是20万吨,但选择20万吨的货轮就超载了,所以要选择21万吨。教师进一步引导学生总结:在这种情况下,不管尾数是多少,都要进一,这种方法叫作进一法。第(2)题是在第(1)的基础上,引导学生用估算的方法进行判断。学生指出600万元不够,教师要启发学生说明理由,因为把“203900吨”往小估是20万吨,30×20=600(万元),说明实际要付的运费大于600万元,所以不够。教师进一步指出,如果要运的吨数是“209300吨”,是否还得看成20万吨进行估算?得到肯定的回答后,教师引导学生总结:不论尾数是多少,都要去尾,这种求近似数的方法叫作去尾法。求一个数的近似数,除了四舍五入法,还有去尾法与进一法这两种方法。
在数学概念的学习中,可以把概念的形成过程转化为数学规律的探究过程,让学生结合具体例子,经历概念的形成、完善与优化,并与有联系的概念进行比较分析,凸显新学习的概念的本质特征。
(1.浙江省杭州市萧山区所前镇第二小学
2.浙江省杭州市萧山区崇文世纪城实验学校)
