发展小学生模型意识的内涵及其教学思考

培养小学生模型意识的思考与实践

“模型意识”是小学生数学核心素养的主要表现之一。如何理解模型意识的本质内涵？如何理解发展小学生模型意识的意义与实质？如何引导学生在学习过程中经历、体验模型的建构与解构？如何把握发展学生模型意识的教学要点？这些都是一线教师在教学中正面临着的问题。《义务教育数学课程标准（2022年版）》颁布后，费岭峰老师与他的研究团队结合具体内容，以促进学生模型意识的发展为目标对课堂教学展开了系列研究。本期特刊发他们的部分研究成果，为广大教师提供教学参考。

【摘   要】模型意识是小学阶段数学核心素养的表现之一，主要指对数学模型普适性的初步感悟。教师结合数学模型的建构过程，从建构与解构两个维度来解读“发展小学生模型意识”的内涵。在教学实践中，教师需要把握三个方面的教学要点，即：在多样的问题解决中感知数学模型的抽象过程，在建模与解模中拉长数学模型的建构体验过程，在多层次运用中感受数学基本模型与变式模型间的关系。

【關键词】模型意识；模型建构；教学要点

模型思想是数学基本思想之一，在小学数学课程内容中有着重要的地位。《义务教育数学课程标准（2022年版）》（以下简称“2022年版课标”）将《义务教育数学课程标准（2011年版）》中提出的“模型思想”分为“模型意识”和“模型观念”两个核心素养的主要表现，在小学阶段重点发展学生的模型意识。那么，建构数学模型的意义是什么？发展小学生模型意识的内涵是什么？对于学生来说，发展模型意识需要经历怎样的学习过程？教师在教学中又需要把握哪些教学要点？为解决这些问题，笔者围绕发展小学生的模型意识进行了实践研究，探索形成了一些“学—教—评”的实践经验。

一、模型意识的内涵释义

2022年版课标将小学阶段的模型意识定位为对数学模型普适性的初步感悟。具体表现在两个层面：一是现实生活中大量的问题与数学有着密切的联系，可以用数学的概念与方法予以解释；二是知道数学模型可以用来解决一类问题，学生可以通过对数学模型的应用，体会数学知识的应用价值。

与初中阶段的模型观念相比，小学阶段的模型意识更侧重于数学模型的建模过程，强调对模型解释、模型应用的感悟。这里的感悟，即感觉与体悟。具体而言，就是不过度追求形式化的表达，不过分强调逻辑的演绎过程，定位于获得初步的理性认识。由此具体解读模型意识的内涵，可以从以下三个层次进行理解。

●层次一：感受到数学模型的建构与大量现实生活中的问题存在着密切联系，初步经历数学模型的建构过程。

●层次二：知道用数学模型可以解决一类问题，并能试着应用模型解决同类问题。

●层次三：碰到生活中的某些问题时，能够有意识地用数学的语言或方法予以解释。

二、发展小学生模型意识的内涵

数学模型的建构过程有其独特的特点。因此，发展小学生模型意识的具体内涵可以从数学模型的建构与解构两个角度进行思考。从模型建构的视角看，要引导学生经历生活问题的数学化建构过程，感悟数学模型与生活问题间的关联性；从模型解构的视角看，要引导学生学会用数学模型解释生活中的一些问题，体会数学模型的抽象性与丰富性，积累模型应用的基本活动经验。

（一）建构视角，即经历建模过程，获得模型建构的体验

小学数学学习强调直观性和情境性，让学生从生活经验出发，结合现实生活中的问题进行探究，形成数学认知结构。在数学模型的建构中，也要结合现实生活中的问题，让学生经历观察、分析和思考，理解数学模型的建构过程。这是学生认识模型，感悟模型的内涵，发展模型意识的必经之路。以对加法的认识为例，教师要让学生经历从事物数量的合并、抽象到数与式的表达，通过多次体验积累丰富的感性经验，理解“把两个数合并成一个数的运算”这一抽象的加法意义。

数学模型的建构一般表现为对模型的感知、发现与逐步抽象的认知行为。模型建构的发展目标具体表现为以下两个方面。

1.经历过程

引导学生经历感知、发现和丰富数学模型的全过程。这里的感知指学生对现实生活中的问题蕴含的内在特质的初步感受；发现指经历对多个蕴含相同特质的问题的多次感受之后，对它们共同特质的发现，并能对此作出一定的结构化表达；丰富指对多个相关问题中的同一特质作出一定的结构化表征之后的延展与完善。比如，在建构“运算律”模型时，学生需要通过对多个实例（即问题或算式）的解答或观察，感知不同背后的相同点，从而发现其中存在的规律，并能尝试借助数学语言（符号）进行表达。

2.体验建构

实际上，在某个数学模型的建构中，学生对同一特质的发现、明晰和结构化表达等，均需要经历建构过程。因此，无论是模型的发现，还是模型的结构化抽象与提炼，均是模型思想的重要内容。对教师而言，有意识地引导学生体验数学模型的建构过程，有利于学生积累数学建模的基本活动经验。

（二）解构视角，即尝试应用模型，丰富模型建构经验

从2022年版课标给出的模型意识的内涵来看，学生模型意识的发展过程中特别注重数学模型的应用。2022年版课标指出：“知道数学模型可以用来解决一类问题，是数学应用的基本途径。”这表明应用模型是发展学生数学模型意识的重要内容。在教学实践中应用模型可以有两种不同方式：一是用数学模型解决同类问题。如用“路程、速度、时间”的关系模型，可以解决“已知速度、时间，求路程”的问题：一辆汽车每小时行60千米，2小时行多少千米？可以解决“已知路程、速度，求时间”的问题：一条轨道长30米，一辆玩具汽车每分钟行5米，几分钟能行完？可以解决“已知路程、时间，求速度”的问题：一辆汽车3小时行驶216千米，每小时行驶多少千米？二是用“概念与方法”解释生活问题。如用“进水与出水”的模型，既可以解释灌溉农田时实际的“进水与出水”问题，还可以解释生活中排队候场情境中的问题。

数学模型的解构建立在基本模型的建构之上，表现为模型的变式与模型的应用。因此，模型解构的发展目标也可以表述为两个方面。

1.数学模型的丰富感知

数学模型的丰富感知以其多元性、多样性为基础。建构数学模型的全过程有基本的路径，而路径是丰富与多样的。如从运算角度来看，有四则运算模型、运算律模型及“用数学”中的问题解决模型。四则运算模型是基于四则运算的“通过算理探索算法”的数学建模过程；运算律模型是基于运算意义进行的“从现象到本质”的运算性质发现与抽象的建模过程；“用数学”中的问题解决模型则是基于运算意义与算法，解决实际问题的“数学知识习得与应用”的模型解构与重构的过程。

比如，学生学习了乘法与除法之后，在后续的学习中又会借助乘除法的运算意义探索数量之间的关系，如前文谈到的与物理量有关的“速度、时间与路程”间的关系以及与个数有关的“单价、数量与总价”间的关系。教师要在学生探索这些数量关系的过程中，启发学生会用数学的语言表达现实世界，丰富乘、除法运算的模型内涵。

2.数学模型的法理体悟

“法理體悟”是数学模型应用的内在逻辑，建立模型思想是学生体会和理解数学与外部世界联系的基本途径。在数学学习过程中，数学模型会呈现不同的显性样态，其思维、方法和逻辑却是相同的，都是从现实生活和具体情境中抽象出数学问题，然后用符号、等式等数学语言表达问题中所蕴含的数量关系和变化规律，这表明数学模型建构方法存在同一性。由此，教师要引导学生明晰数学模型的探索意义，发展学生的数学模型意识。当某种数学模型出现变式时，要帮助学生体悟相关模型的内涵本质存在同一性。

比如，对于“减法的性质”，一般表述为：一个数连续减去几个数，可以用这个数减去这几个数的和，结果不变。用字母表示为a-b-c=a-（b+c）。在应用过程中，还会产生一些变式，如a-b-c=a-c-b，a-（b-c）=a-b+c等，其本质都是加法运算律的变式。

三、发展小学生模型意识的教学要点

上述探讨过程中，笔者结合2022年版课标中关于模型意识的内涵，具体分析了发展小学生数学模型意识的目标定位。而达成这些目标需要把握以下三个方面的教学要点。

（一）在多样的问题解决中感知数学模型的抽象过程

现实生活问题、数学情境是抽象数学模型的载体。在解决相关问题的过程中，对同类问题的解答，能促使学生通过体验、感知、比较、分析等方法，抽象出数学模型。如解答如下问题：

（1）一辆汽车每小时行驶60千米，4小时行驶多少千米？

（2）小东每分钟走70米，4分钟走多少米？

（3）猎豹每秒可奔跑30米，4秒能跑多少米？

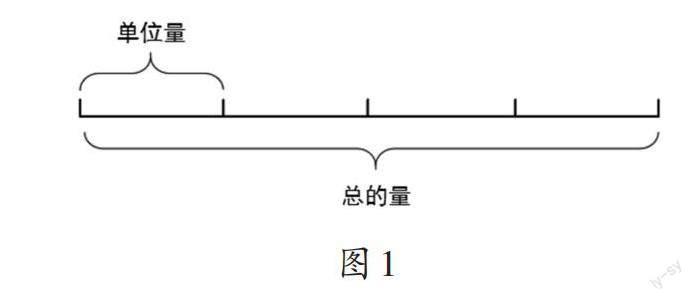
学生在解答这三个问题的过程中，会产生三个不同水平层次的认知：水平一，基于原有经验，这三个问题均可以用乘法运算来解答，即60×4、70×4和30×4；水平二，这三个问题中，第一个量都是“速度”，第二个量都是“时间”，最后都求解相应时间内所行走的“路程”，都可以用“速度×时间”来计算；水平三，若需要用一个图来表示这些问题中相应数量的关系，可以用图1来表达。从图中可以看出单位时间内的量（单位量），以及4段即4个单位时间的量（总的量）。求总的量，即算出4个单位时间的量，符合乘法的运算意义，因此可用乘法计算。

用此图来解释以上三个问题时，能将问题中数量之间的关系准确地表征出来。学生也就能够直观地感受到三个问题本质的同一性：求4个相同量的和，可用乘法计算。以上三个水平的认知，便是学生对“速度、时间、路程”这一关系模型的逐步抽象过程。

（二）在建模与解模中拉长数学模型的建构体验过程

研究表明，数学知识的学习需要经历一个完整的过程，在习得知识技能的同时获取相应的基本活动经验。建构模型的过程中，不仅要有数学归纳、抽象的过程，还要有数学演绎、应用的过程。数学归纳、抽象是初步建构模型的必要环节，数学演绎、应用则是理解模型内涵的必要环节。

以一年级“加法模型”的建构教学为例来作具体阐述。加法模型实质上表达的是两个数（或量）的合并，即将两个不相交的有限集合A和B中的元素，合并成一个新的集合C（即集合A与集合B的并集）。在“认识加法”的学习中，教师要引导学生通过三个层次的学习活动，建构“加法模型”：活动一，看不同情境，说不同的加法算式；活动二，看不同情境，写相同的加法算式；活动三，看某个加法算式，想象不同情境。［1］

三个层次的活动中，前两个活动指向模型的发现、抽象，后一个活动指向模型的理解与应用。整个学习过程既充分体现了数学模型与现实生活问题之间的关联，又表现了应用模型解释现实生活问题的过程。

（三）在多层次运用中感受数学基本模型与变式模型间的关系

数学模型的建构并不止于抽象和结构化提炼，还需结合应用模型的解释、解答等多层次应用，进一步体验基本模型与变式模型的关系，从而完善对基本模型的认识，感受数学模型的应用价值。

例如，在人教版教材五年级上册“植树问题”的教学中，教师一般会引导学生抽象出解决植树问题的基本模型——“两端都种”的模型，即“路的总长÷段数+1=棵数”，然后在学生应用模型的过程中，引入变式模型，即“一端种”和“两端都不种”的情况。将“两端都种”的问题作为基本问题来解答，就是在抽象基本模型；基于此，在学生有了对基本模型的感知理解后，再引导学生结合现实问题的解决，认识变式模型。整个过程中，学生既在多层次的深度应用中完善了解决植树问题的模型结构，又加深了对解决此问题的基本模型与变式模型间关系的理解，认识到植树问题是除法运算应用中的一类典型问题，主要研究段数与点数之间的关系，而基本模型与变式模型只是基于实际情境的特殊性分析作的恰当选择而已。

总之，发展小学生模型意识的过程，实质上就是引导学生经历、体验从现象认识到本质理解的数学知识的学习过程，是培养学生数学眼光、数学语言、数学思维的重要过程。因此，在日常的教学实践中，一线教师应对其给予密切关注，切实发展小学生的模型意识。

参考文献：

［1］费岭峰.数学模型思想及其教学策略初探［J］.小学教学研究，2013（2）：11-13.

（浙江省嘉兴市南湖区教育研究培训中心）