考虑齿面闪温的风电齿轮箱裂纹故障特征分析

2024-03-21张旭钟家欣李伟

机械科学与技术 2024年2期

张旭，钟家欣，李伟

（1.天津工业大学天津市现代机电装备技术重点实验室天津 300387；2.天津城建大学能源与安全工程学院天津 300384）

齿轮箱作为风力发电机组中变速的关键部件，通常承受随机风冲击与电网波动双重载荷的作用，容易发生局部故障和分布式故障[1]。其中，齿轮表面出现裂纹是齿轮箱最常见的局部故障之一。当裂纹扩展到一定程度时，轮齿将会发生断裂，引起更大的啮合冲击，甚至造成整个齿轮的完全失效，最终影响风力发电机组的安全、可靠运行[2]。此外，齿轮啮合过程中齿面摩擦会在啮合处产生大量的热，造成啮合表面温度升高，以至啮合点周围出现局部变形，从而影响齿轮的刚度[3]。因此，进行计及齿面闪温影响的齿轮裂纹故障特征研究对风电齿轮箱的故障状态与程度监测具有重要的理论意义和工程应用价值。

齿根裂纹会影响齿轮的时变啮合刚度，利用势能法、有限元法、实验法等可以对其进行准确计算。其中，势能法的计算效率最高，故国内外学者多采用其开展齿轮裂纹啮合刚度计算的研究[4-6]。Wan等[7]提出一种改进的时变啮合刚度算法，考虑横向和扭转振动方向建立含有轮齿裂纹齿轮转子系统耦合动力学模型，分析裂纹故障对振动响应的影响。Wang 等[8]应用势能法计算包含弯曲刚度、剪切刚度、轴向压缩刚度、赫兹刚度和圆角基础刚度的直齿轮副裂纹时啮合刚度，研究不同裂纹水平对齿轮动力学特性的影响。Yang 等[9]利用势能法得到含有齿根裂纹的直齿圆柱齿轮啮合刚度，通过峰值、均方根值、峰值因子等统计指标评估齿轮系统的振动行为和故障条件。肖正明等[10]采用改进能量法计算正常与含裂纹齿轮时变啮合刚度，建立行星齿轮传动系统动力学模型，研究故障对系统动力学特性的影响，并通过台架实验，对比分析正常与故障齿轮的频域特性。孟宗等[11]通过势能法计算齿根裂纹时的啮合刚度并建立6 自由度齿轮系统动力学模型，研究不同裂纹长度下的时域特性，并比较分析多种统计指标随裂纹扩展程度的变化趋势。

许多学者也在温度对齿轮动力学特性的影响方面取得了一些研究进展。Gou 等[12]考虑齿面闪温、时变啮合刚度、齿面摩擦、齿侧间隙和综合啮合误差建立齿轮-转子-轴承系统动力学模型，并进行非线性动力学行为分析。张笑等[13]建立计入热变形的齿轮系统动力学模型，研究不同转矩波动频率下温度对系统动力学响应的影响。田亚平等[14]建立含齿面闪温的直齿轮副非线性动力学模型，分析系统分岔、齿面冲击、齿面脱啮和动载系数的变化规律。Pan 等[15]考虑齿面接触温度、摩擦、载荷波动等非线性特征，建立齿轮-轴-轴承传动系统耦合动力学模型，研究温度对齿轮系统动力学特性的影响。

以上关于裂纹和温度对齿轮动力学特性影响的研究多是单独展开的，并未进一步分析计及齿面闪温时齿根裂纹对齿轮系统动态特性的影响。基于Blok 闪温理论和热变形公式，利用Hertz 接触理论获得考虑齿面闪温因素的轮齿刚度；建立含有高速级齿轮裂纹故障的风电齿轮箱动力学模型，推导系统振动微分方程并求解动力学响应；分析齿根裂纹故障的仿真与实验的时频域特性，研究齿面闪温对不同裂纹程度下齿轮振动特性的影响。

1 风电齿轮箱动力学模型建立

1.1 齿轮箱动力学模型建立

不考虑齿轮的横向振动位移，采用集中质量法对两级定轴齿轮和一级行星轮组成的风电齿轮箱（图1）建立多级齿轮传动系统纯扭转动力学模型，如图2 所示。

图1 齿轮传动系统实验台Fig.1 Test platform of the gear transmission system

图2 齿轮传动系统纯扭转动力学模型Fig.2 Pure torsional dynamic model of the gear transmission system

图2 中，Tin为输入转矩，Tout为输出转矩，r为内齿圈；1、2 为高速级主、从动齿轮，3、4 为中速级主、从动齿轮，s为太阳轮，pn（n=1,···,4）为4 个行星轮，c为行星架，对应的转角为θ1、θ2、θ3、θ4、θs、θp1、θp2、θp3、θp4、θc；kj、cj、bj、ej(j=1,2,spn,rpn)分别为高速级齿轮间、中速级齿轮间、太阳轮和第n个行星轮间、内齿圈与第n个行星轮间的时变啮合刚度、阻尼、齿侧间隙、综合啮合误差。

定义啮合线上齿轮的相对位移为：

式中：rb1、rb2、rb3、rb4、rbs、rbpn、rbc分别为高速级主、从动轮，中速级主、从动轮，太阳轮，行星轮和行星架的基圆半径。

1.2 系统动力学方程建立

根据拉格朗日方程建立如图2 所示系统的振动微分方程组[16]为：

式中：I1、I2、I3、I4、Is、Ipn、Ic为高速级主、从动轮，中速级主、从动轮，太阳轮，行星轮，行星架的转动惯量。

将式（1）代入式（2）可得：

阻尼系数cj表达式为

式中：ξ为啮合阻尼比，取0.03 ～ 0.17；km为啮合刚度平均值；m1、m2为主、从动轮的质量。

齿轮副的综合啮合误差ej(t)可用啮合函数的一次谐波形式表示，即

式中：eaj、 φj分别为第j级齿轮副综合啮合误差的幅值及其初始相位。

齿侧间隙非线性函数为：

定义无量纲时间 τ=ωnt，其中固有频率km1为高速级齿轮副啮合刚度的平均值，u=lx（l为特征长度，l=b1）。

归一化方程（3），得到振动微分方程组为：

量纲一齿侧间隙非线性函数为：

将轮齿简化为齿根圆上的悬臂梁如图3 所示。

图3 齿轮轮齿悬臂梁模型Fig.3 Cantilever beam model of the gear tooth

采用文献[17] 的势能法计算齿轮啮合刚度。啮合齿轮副的刚度被假定包括剪切刚度ks、弯曲刚度kb、轴向压缩刚度ka、赫兹接触刚度kh，表达式分别为：

单对齿轮副总啮合刚度为每个齿轮的剪切刚度、弯曲刚度、轴向压缩刚度以及赫兹刚度的总和，即

式中：kt1为第一对轮齿啮合刚度。

当两对轮齿啮合时，第二对轮齿啮合刚度为kt2，双齿啮合的总有效啮合刚度kt为

2 计及齿面闪温的轮齿刚度计算

2.1 齿面闪温计算

齿面接触温度TB由本体温度TM和齿面瞬时闪温Tf组成，即

根据Blok 闪温理论，齿面瞬时闪温[18]为

式中：u为温升系数，对齿轮副取0.83；fµ为摩擦因数；fn为齿面法向载荷；gi为齿轮系统热传导系数；ρi为齿面密度；ci为比热容；b为齿宽；B(t)为齿面接触带半宽；Vi(t)(i=1,2)为主、从动轮齿面切向速度。

式中： ωi为角速度；齿面啮合压力角Rci(t)(i=1,2)为啮合点到主、从动轮圆心的距离。Rci(t)的表达式为：

式中：rbi(i=1,2) 为主、从动轮基圆半径；ra2为从动轮齿顶圆半径； α为分度圆压力角。

啮合点的接触半宽B(t)为

式中： ψ为计算系数， ψ=1.128； ν 为泊松比；E为弹性模量；ri(t)(i=1,2)为主、从动轮啮合点处齿廓曲率半径。

2.2 齿面闪温引起的轮齿齿廓变形计算

齿面温度变化使齿轮实际齿廓与理论齿廓不重合，得到主、从动轮齿廓形变 δi(t)[12]为

式中：负号表示齿廓向外膨胀； ∆T为齿面接触温度和本体温度之间的差值； λ为材料的线膨胀系数；齿面热变形后的压力角ubi为系统稳定工作时齿轮的基圆热变形量。

式中：r0i为齿轮轴半径；t(r0i)、t(rbi)分别为齿轮稳定工作时齿轮轴和基圆面温度；li(t)(i=1,2)为主、从动轮啮合处的齿厚。

2.3 轮齿刚度计算

根据Hertz 接触理论，齿面闪温引起的主、从动齿轮刚度kwi(t)(i=1,2)为

齿轮啮合时两个齿面产生的形变在同一条直线上，则闪温引起的啮合刚度kw(t)为

考虑齿面闪温后的总啮合刚度kwt[14]为

2.4 齿面闪温特性分析

载荷分别为fn=6 kN 和30 kN 时，齿轮啮合过程中齿面闪温的变化如图4 所示。

图4 齿面闪温随啮合点变化的趋势Fig.4 Change trend of tooth flash temperature with the meshing point

可以看出，随着载荷的增加，齿面闪温有较大的增幅；同一载荷下，齿面闪温在主动轮齿根进入啮合时达到峰值，啮合过程中逐渐降低，啮合节点处变为最低，并随着轮齿继续啮合，在齿顶位置又出现较高值。齿面闪温在啮合节点处为零是由于两齿面间的相对滑移速度为零，在齿顶和齿根处最大则是因为相对滑移速度更大，表明齿面闪温的变化与齿轮啮合中滑移速度相关。本文关于齿面闪温计算的结果变化趋势与文献[12]、文献[19]均一致。

3 含裂纹时齿轮啮合刚度计算

假设裂纹从高速级齿轮主动轮轮齿危险区域A点开始沿直线传播，达到齿轮中心线上B点后改变传播方向向C点扩展，直到轮齿断裂，如图5 所示。裂纹会引起齿长和齿高的变化，进而影响弯曲刚度和剪切刚度。裂纹状态下轮齿的弯曲刚度和剪切刚度为：

图5 裂纹轮齿模型Fig.5 Model of the tooth with crack

将表1 中4 种裂纹情况下的参数代入式（23），得到图6 所示啮合刚度。可以看出，啮合刚度随着裂纹长度的增大而逐渐减小。

表1 高速级主动轮裂纹故障参数Tab.1 Parameters of crack faults of the high-speed driving gear

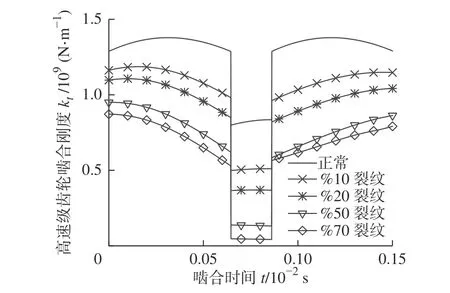
图6 高速级齿轮在不同裂纹状态下的啮合刚度Fig.6 Meshing stiffness of high-speed gears under different crack states

裂纹故障状态下时变啮合刚度可展开[20]为

式中：kai、kaj、 φi、 φj为正常、裂纹时刚度幅值系数及相位角；fm为啮合频率；fp为裂纹故障特征频率。

4 齿轮裂纹故障特征分析

基于高速级齿轮副中主动轮产生裂纹的齿轮箱动力学模型，计算有无齿面闪温时不同裂纹程度下齿轮系统动力学响应。齿轮箱各齿轮参数如表2 所示，Tin=6.5 Nm，Tout=8.5 Nm，eaj=2 μm，bj=5 μm。

表2 齿轮箱各齿轮参数Tab.2 Parameters of gears in the gearbox

4.1 不考虑齿面闪温的裂纹故障特征分析

利用Runge-Kutta 法求解式（7），得到不考虑齿面闪温时高速级齿轮正常和10%、20%、50%、70%裂纹状态下的时域图、频谱图、相图和Poincaré截面，如图7 所示。

由图7a）～图7e）的时域图、频谱图、相图、Poincaré截面可以看出，齿轮产生裂纹后，加速度时域响应在原始的持续振荡信号上叠加谐波信号，出现周期性冲击且随着裂纹程度的增大而愈发明显；频域上出现故障频率fd及其倍频，中速级啮合频率f2的幅值增大，高速级啮合频率f1附近出现带宽为fd的边频带，且随着裂纹程度的增加，fd的幅值增大且边频增多；相图形状由环带变为不规则曲线，且曲线范围随着裂纹程度的增加而逐渐扩大；Poincaré截面形状由点团变成点环，系统运动由周期变为混沌且稳定性随裂纹程度的增加而逐渐降低。造成时频域具有上述变化规律的原因是高速级齿轮裂纹引起的啮合齿面载荷波动致使振动的幅值和频率发生变化，进而产生信号调制现象。

4.2 裂纹故障特征实验验证

基于风电机组故障诊断综合试验台，在高速级齿轮主动轮齿根上设置裂纹故障，采集正常、裂纹状态下定轴齿轮箱箱体表面的加速度振动信号，并利用傅里叶变换作频谱图（图8）。其中，裂纹长度q1=1 mm，裂纹角度为70°，电机转频为40 Hz。

图8 时频域实验结果Fig.8 Experimental results in the time-frequency domain

由图8 可以看出，裂纹产生的冲击使加速度幅值明显增大；裂纹状态下，高速级啮合频率（f1=1）周围有间隔大小为fd的边频，轴频fz与其大小相等的fd叠加导致幅值有所增大。综上所述，齿根裂纹故障的实验与仿真时频域分析结果具有相同的变化规律。

4.3 考虑齿面闪温的裂纹故障特征分析

基于考虑齿面闪温且含齿根裂纹的齿轮系统动力学模型，计算得到正常及10%、20%、50%、70%裂纹状态下的齿轮动力学响应曲线，如图9 所示。

图9 考虑齿面闪温时的动力学响应Fig.9 Dynamic responses with the tooth flash temperature considered

对比图7、图9 可以看出，考虑齿面闪温后，系统运动状态并未发生变化；正常工况下时域和频域的响应幅值有所增大，相图位置右移；裂纹状态下加速度时域图中产生的冲击幅值增大，频谱图中故障频率及其倍频的幅值明显增大且高速级啮合频率周围的边频带结构更加复杂，相图曲线范围逐渐向外扩展，Poincaré截面中点环周围离散点增多，混沌运动更为复杂。相较于10%、20%裂纹，50%、70%裂纹时的动力学响应受闪温影响更为明显。