混合动力汽车功率分流传动系统扭转振动及其影响因素研究

王欢 , ，葛帅帅，姜艳军，张志刚，郭栋，李明

（1.重庆理工大学 汽车零部件先进制造技术教育部重点实验室，重庆 400054；2.重庆青山工业有限责任公司技术中心，重庆 402776）

随着国家提出碳达峰和碳中和目标，汽车作为碳排放和空气污染的重要来源，对其排放要求越来越严格[1]。混合动力汽车相对于传统燃油汽车排放量小，更容易满足排放法规要求。同时其相对于纯电动汽车，更易于补充燃料，不存在里程焦虑问题。

汽车动力传动系统中动力源振动、传动系统弯曲振动和驱动桥振动等其振动之间相互影响共同构成了动力传动系统振动与噪声问题[2-3]。当传动系统受到外界激励，如动力源、路面以及车轮跳动产生的周期性扭转激励与传动系统固有频率相近时，会发生共振，并产生较大的共振载荷，进而影响零部件可靠性[4]。同时还会引起车身垂向振动和纵向振动以及声音干扰，进而影响汽车舒适性[5-6]。混合动力汽车传动系统相对于传统燃油汽车结构更为复杂，动力源增加了一个或者多个电机，运行工况更加多变，导致其扭转振动问题突出，严重影响传动效率、零部件使用寿命和乘客舒适性[7]。

目前关于混合动力汽车传动系统扭转振动方面的研究较少，主要是通过建立传动系统扭转振动模型，对扭转振动特点进行分析。孟德建等[8]建立了包含发动机、电机和行星齿轮的混联式混合动力汽车传动系统扭转动力学模型，分析了多种工作模式下传动系统的固有特性和瞬态响应。严正峰等[9]采用键合图法对使用限扭减振器的混合动力汽车传动系统进行动力学建模，并通过MATLAB/Simulink软件对限扭减振器参数进行仿真计算。于福康[10]针对采用无级变速箱的混合动力汽车进行扭转振动分析，通过使用双质量飞轮并对其参数进行优化从而解决传动系统振动问题。张立军等[11]建立了包括发动机、电机、单行星排的传动系统扭转振动模型，通过功率控制策略分析了典型工作模式下的瞬态振动响应。Shimode 等[12]将分析多元复杂关系的机器学习应用到发动机启动扭转振动分析中，通过机器学习提取新的影响因素，并分析了其对传动系统扭转振动的影响规律。

目前国内外针对混合动力汽车功率分流传动系统扭转振动问题进行了一些研究，但是针对复合行星齿轮机构，特别是混合动力汽车多工况、多动力源、多输入多输出的扭转振动问题研究较少，同时目前研究中建立的动力学模型较为简单，对复合行星齿轮机构中齿轮副啮合等简化较多，而这些因素对传动系统扭转振动影响较大。因此，综合考虑发动机、电机、复合行星齿轮机构、离合器、减速器、差速器和半轴等部件，建立混合动力汽车功率分流传动系统动力学模型，深入研究其固有特性及其影响因素，对于改善混合动力汽车扭转振动具有重要的理论意义及应用价值。

1 功率分流传动系统动力学建模

1.1 混合动力汽车功率分流传动系统

以某款混合动力汽车传动系统为研究对象，结构如图1 所示。混合动力汽车传动系统的核心部件是功率分流装置，其将动力进行合理分配，使汽车在满足动力性的前提下达到理想的燃油经济性，因此传动系统模型的关键在于功率分流装置模型，本文采用的功率分流机构是复合行星排[13]。电机E1 为辅助电机和小太阳轮S1 连接，主要负责启动发动机和发电。电机E2 为驱动电机和大太阳轮S2 连接，主要负责驱动和制动时进行能量回收转化。发动机通过扭转减振器d 与功率分流装置中的行星架c 连接。功率分流装置既承担了功率分流作用，也充当了变速器的作用。功率分流装置齿圈和减速器通过齿轮副啮合，最后通过差速装置将动力传递给半轴，半轴将动力传送到车轮上，实现驱动汽车。

图1 混合动力汽车传动汽车传动系统结构Fig.1 Structure of hybrid electric vehicle's transmission system

本文采用的复合行星排（图2）与拉维娜式行星轮系（图3）结构相似，均为两个单行星轮系组合，且共用了一个行星架和齿圈。前排轮系的小太阳轮和短行星齿轮啮合，后排轮系的大太阳轮和长行星齿轮啮合；长行星齿轮和短行星齿轮啮合，通过短行星齿轮将动力传递给内齿圈。

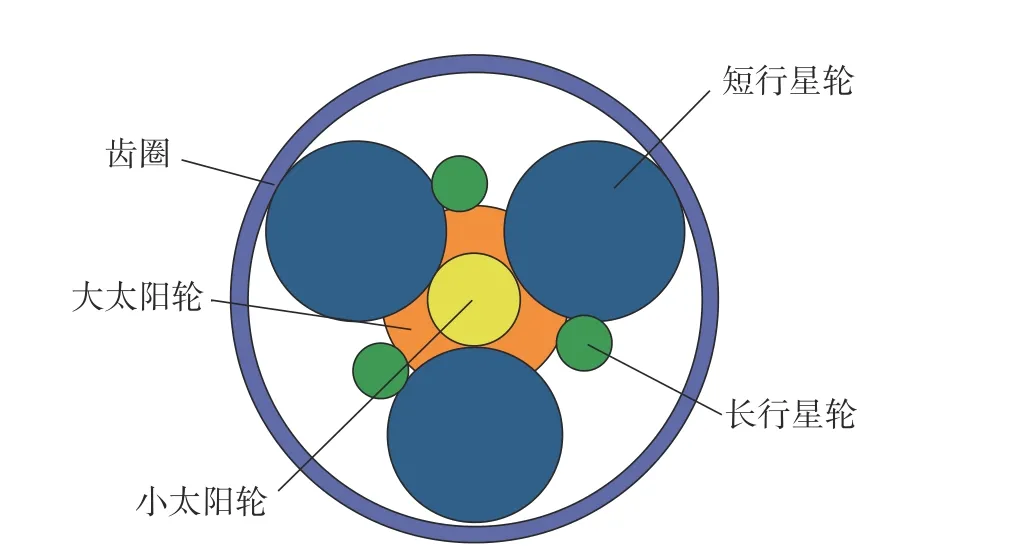
图2 复合行星齿轮机构Fig.2 Composite planetary gear mechanism

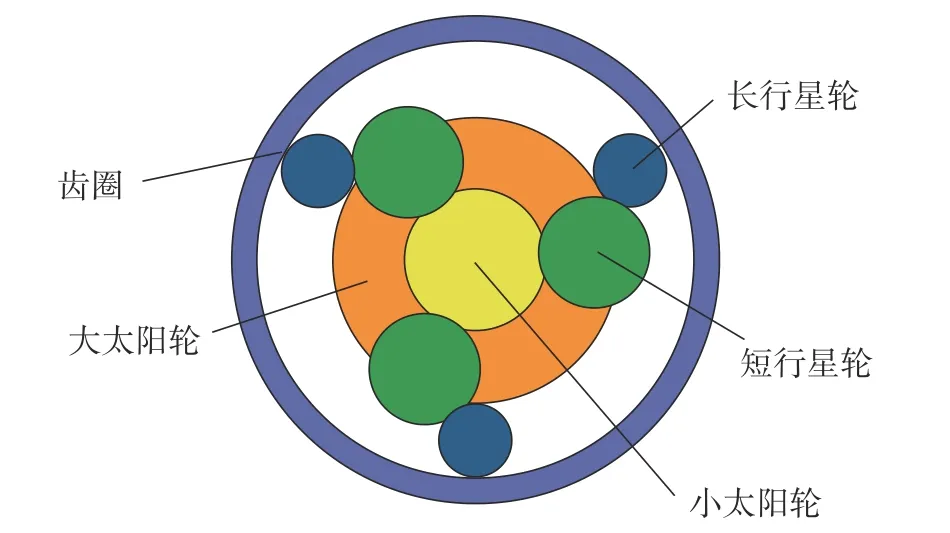
图3 拉维娜式复合行星轮系结构图Fig.3 Structure diagram of Lavina type composite planetary gear system

和拉维娜结构相比，复合行星齿轮结构可以增大后排行星齿轮的杠杆效能。在功率分流装置中，电机E1 和小太阳轮连接，电机E2 和大太阳轮连接，发动机与行星架连接。由于电机的功率直接影响着电机成本，采用复合行星齿轮结构后可以有效降低电机峰值功率，从而降低电机成本，同时也可以规避丰田公司THS 专利的限制。根据复合行星齿轮的结构原理，可以计算出发动机的转速nf和齿圈的转速nc分别为：

式中：nxt为小太阳轮转速；ndt为大太阳轮转速；i1为齿圈内齿和小太阳轮的齿数比；i2为齿圈内齿和大太阳轮的齿数比。

1.2 功率分流装置动力学模型

1.2.1 功率分流装置动力学模型

复合行星排动力学模型包括行星架、小太阳轮、大太阳轮、3 个短行星齿轮、3 个长行星齿轮和齿圈。建立功率分流装置10 自由度无阻尼自由振动模型，如图4 所示。

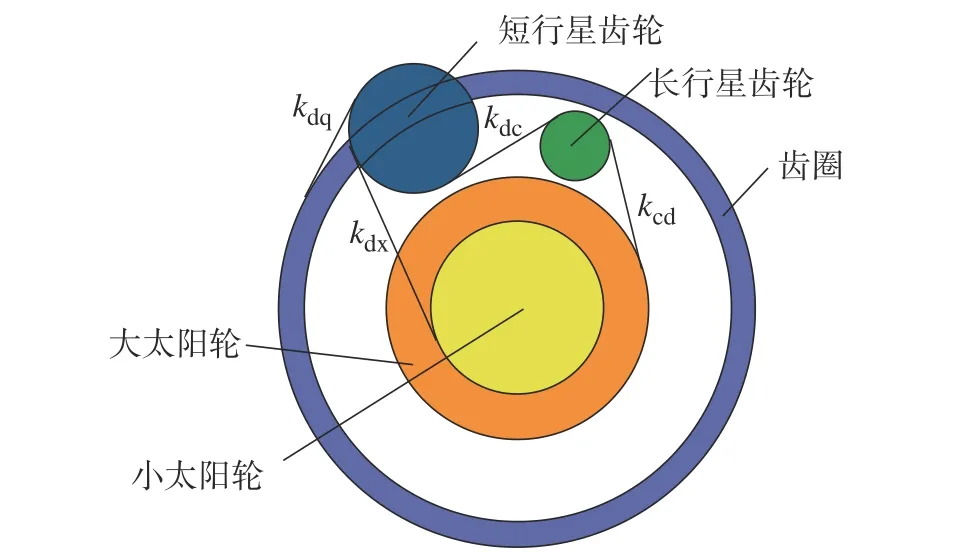
图4 复合行星齿轮的动力学模型Fig.4 Dynamic model of composite planetary gear

广义坐标为

式 中： θxxj,θxt,θdt,θdx1,θdx2,θdx3,θcx1,θcx2,θcx3,θcq分 别为行星架、小太阳轮、大太阳轮、短行星齿轮1、2、3、长行星齿轮1、2、3 和齿圈的角位移。

规定齿轮逆时针转动方向为正方向，则复合行星齿轮无阻尼振动的动能和势能之差为：

式中：Jxxj、Jxt、Jdt、Jdxi、Jcxi、Jcq分别为行星架、小太阳轮加电机E1、大太阳轮加电机E2、短行星齿轮1、2、3、长行星齿轮1、2、3、齿圈的转动惯量；kdx、kcd、kdc、kdq分别为短行星齿轮和小太阳轮的啮合刚度、长行星齿轮和大太阳轮的啮合刚度、短行星齿轮和长行星齿轮的啮合刚度、短行星齿轮和齿圈的啮合刚度；Rxt、Rdt、Rdxi、Rcxi、Rcqn分别为小太阳轮、大太阳轮、短行星齿轮、长行星齿轮、齿圈内齿的基圆半径；mdxi、mcxi分别为短行星齿轮和长行星齿轮的质量；Rdxz、Rcxz分别为短行星齿轮、长行星齿轮基圆到中心的距离。

根据Lagrange 方程求出复合行星排方程为

式中：M为质量矩阵；Kmn为刚度矩阵。

式中：m=1,2,...,10;n=1,2,...,10。

刚度矩阵中各元素为：

其他的Kmn均为0。

1.2.2 齿轮副啮合刚度

复合行星排通过齿轮副啮合传递动力，需要确定各个独立部件连接的刚度，因此先求解传动系统各啮合副的啮合刚度。本文采用Weber 能量法计算齿轮啮合刚度，如图5 所示。

图5 Weber 能量法示图Fig.5 Weber energy method

单个齿轮顺着啮合线的变形量大小 δi表达式为

式中： δz为由齿面弯曲和受到剪切力的形变量； δr为基础部分倾斜产生的变形量。

当一对齿轮副啮合时，每个齿轮在受力作用点沿啮合线的总变形量 δ的表达式为

式中 δ1和 δ2分别为单个齿轮的变形量大小。

式中p1和p2分别为每个齿轮齿面在接触点处的曲率半径。

计算得到的啮合刚度曲线如图6 所示。仿真计算得到各齿轮副啮合刚度如表1 所示。

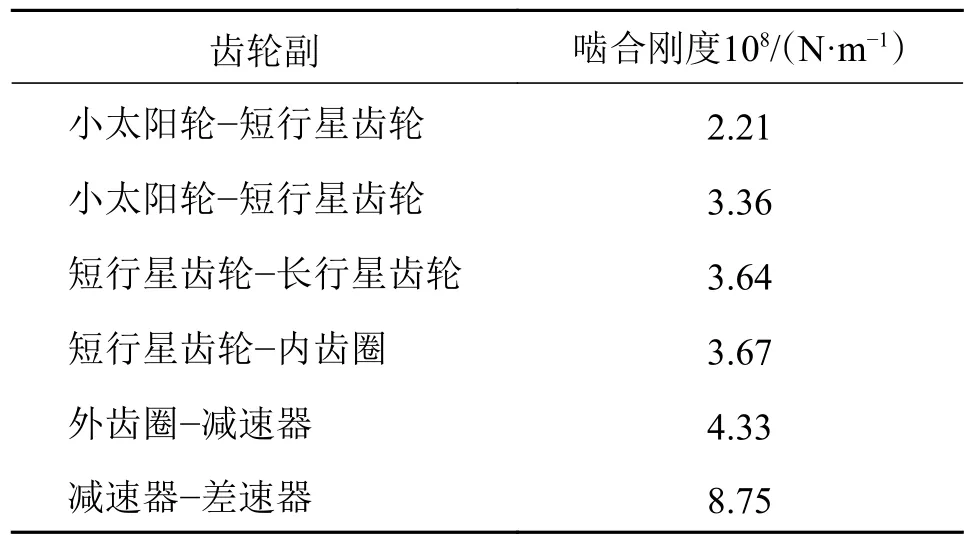
表1 齿轮副啮合刚度Tab.1 Gear pair meshing stiffness

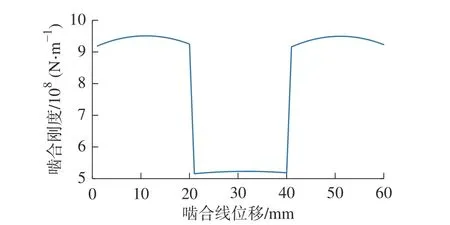
图6 Weber 能量法啮合刚度曲线Fig.6 Weber energy method's meshing stiffness curve

1.3 传动系统动力学模型

1.3.1 发动机简化模型

由于发动机不是本文的主要研究对象，故将发动机看为一个整体，转动惯量等效到飞轮上。

1.3.2 离合器动力学模型

离合器的前部分与发动机飞轮连接、后部分与功率分流装置的行星架连接。由于离合器中的扭转减振器起到减振作用，故将离合器前部分等效到发动机飞轮上，后部分等效到行星架上面，等效于飞轮和行星架之间只存在扭转减振器，如图7 所示[14]。发动机、减振器和行星架部分动力学方程分别为：

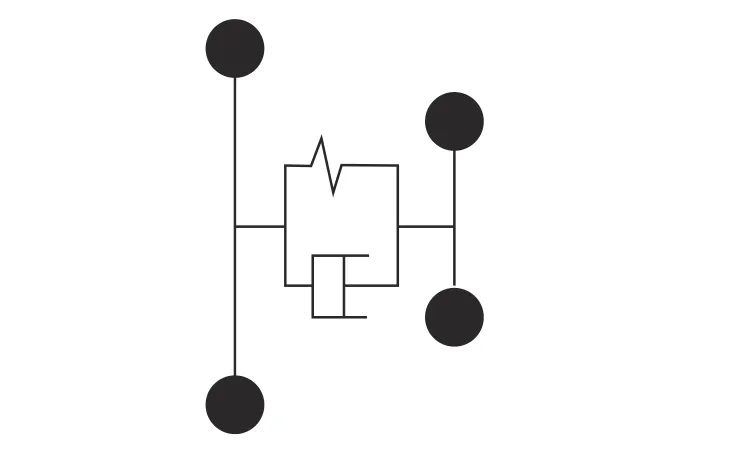
图7 离合器动力学模型Fig.7 Clutch dynamics model

式中：JE为发动机的转动惯量；kjz为减震器刚度；kxxj为行星架扭转刚度； θE为发动机角位移。

1.3.3 电机简化模型

电机E1、E2 转子部分与小太阳轮和大太阳轮连接，定子部分固定在动力合成箱的壳体上。所以将电机E1 和E2 的转动惯量分别等效到小太阳轮和大太阳轮上。

1.3.4 减速器、差速器动力学模型

本文主要分析汽车直线行驶情况，差速器将动力进行平均分配。所以外齿圈、减速器和差速器部分的动力学方程为

式中：Jjs为减速器的转动惯量；kcr为齿圈外齿和减速器的啮合刚度；krc为减速器和差速器主动齿轮的啮合刚度；Rjd、Rjx、Rwcq、Rcsq分别为减速器大齿轮、减速器小齿轮、齿圈外齿、差速器主动齿轮的基圆半径； θjs、 θcq、 θcsq分别为减速器、齿圈、差速器主动齿轮的角位移。

1.3.5 半轴动力学模型

由于差速器将动力平均分配给左右车轮，因此差速器和半轴的动力学方程为

式中：Jcsq为差速器的转动惯量；klt、krc分别为左右半轴的扭转刚度； θlt、 θrt分别为左右车轮的角位移。

1.3.6 传动系统动力学模型

由于车轮的转动惯量较大，故将车身质量等效到车轮上。左右车轮与车身的动力学方程:

整车等效动力学方程:

式中：Jlt、Jrt、Jz分别为左右车轮和整车的转动惯量；ktire为车轮扭转刚度； θz为整车等效角位移；m为整车质量；Rtire为车轮半径。

传动系统动力学方程为

式中：Mz为系统质量矩阵；kz为刚度矩阵。

传动系统各部件参数如表2 所示。

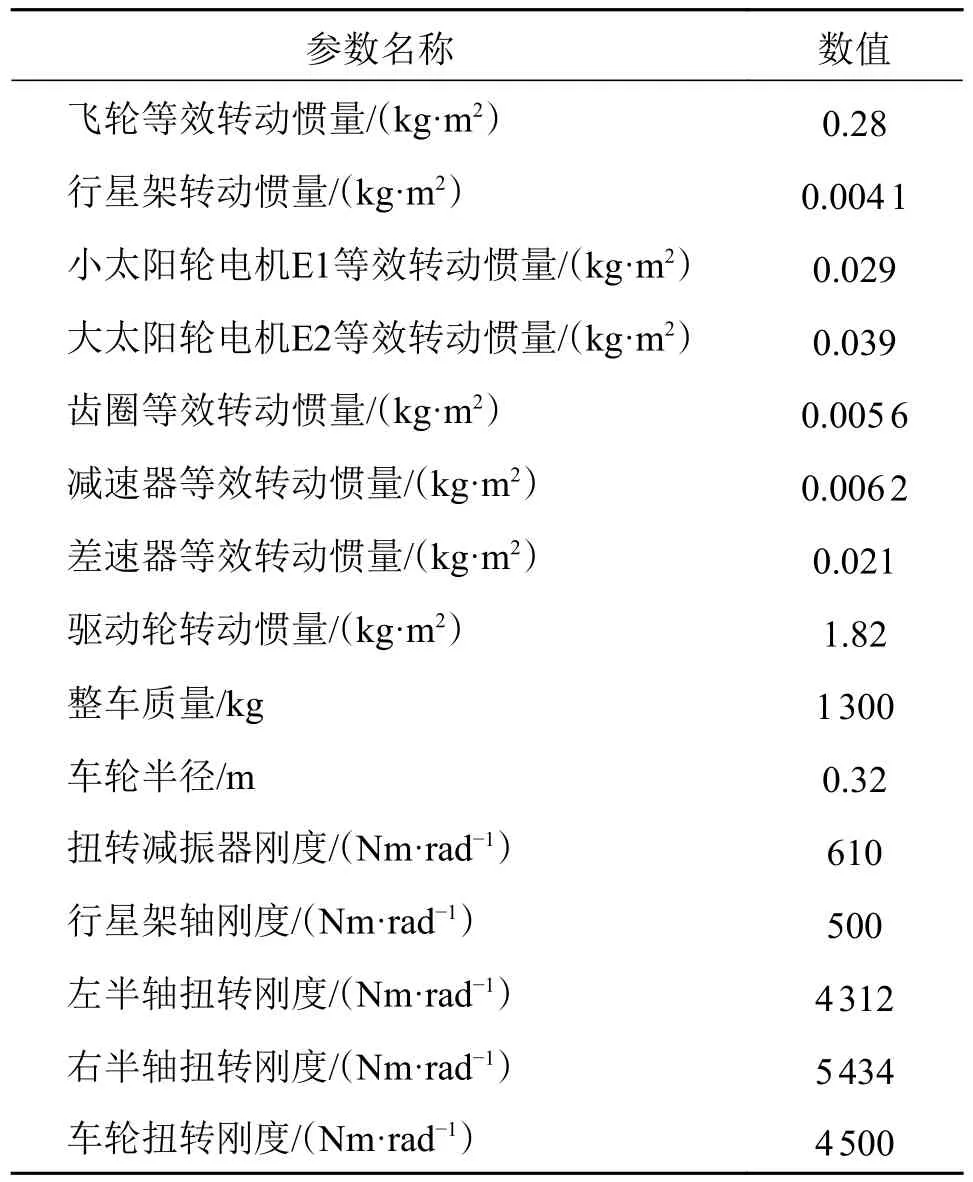
表2 传动系统各部件参数Tab.2 Parameters of various components of the transmission system

2 功率分流传动系统固有特性分析

混合动力汽车存在多种工况，本文主要研究纯电动工况、混动中低速工况和混动高速巡航工况。通过MATLAB 软件，对建立的动力学模型进行仿真，得到传动系统固有频率和振型。由于篇幅限制，以下主要对前8 阶振型进行分析[15]。

2.1 纯电动工况传动系统固有特性

起动和制动能量回收均为纯电动工况。起动时行星架锁死，将发动机与传动系统断开，通过电机驱动车轮。制动时断开发动机，通过电机发电和辅助制动实现制动能量回收。除去发动机和行星架，将传动系统简化为14 自由度扭转振动系统，仿真得到纯电动工况系统固有频率如表3 所示。通过矩阵迭代法依次得到对应的主振型，如图8 和图9 所示。

表3 电动工况传动系统固有频率Tab.3 Natural frequency of electric working condition transmission system

图8 纯电动工况1 ～ 3 阶振型图Fig.8 1-3th order vibration modes of pure electric operating conditions

图9 纯电动工况4 ～ 7 阶振型图Fig.9 4-7th order vibration modes of pure electric operating conditions

图8 和图9 中横坐标振型节点依次代表小太阳轮E1、大太阳轮E2、3 个短行星齿轮、3 个长行星齿轮、齿圈、减速器、差速器、左右驱动车轮和车身。可以看出在纯电动工况1 ～ 3 阶固有频率下，车轮的振动幅度较大，整车存在轻微振动。纯电动工况4 ～ 7 阶固有频率下，小太阳轮和大太阳轮存在小幅度的振动，短行星齿轮和长行星齿轮振动幅度很大，同时减速器、差速器也存在一定程度的振动。

2.2 混动中低速工况传动系统固有特性

在混动中低速工况下，发动机和电机E2 共同驱动车轮。由于车速较低，为了保证发动机工作在燃油经济性最佳区域，发动机多余的动力会通过电机E1 给电池充电。所以此工况下传动系统为16 自由度振动模型。通过仿真计算得到各阶固有频率如表4 所示。通过矩阵迭代法依次得到对应的主振型，如图10 和图11 所示。

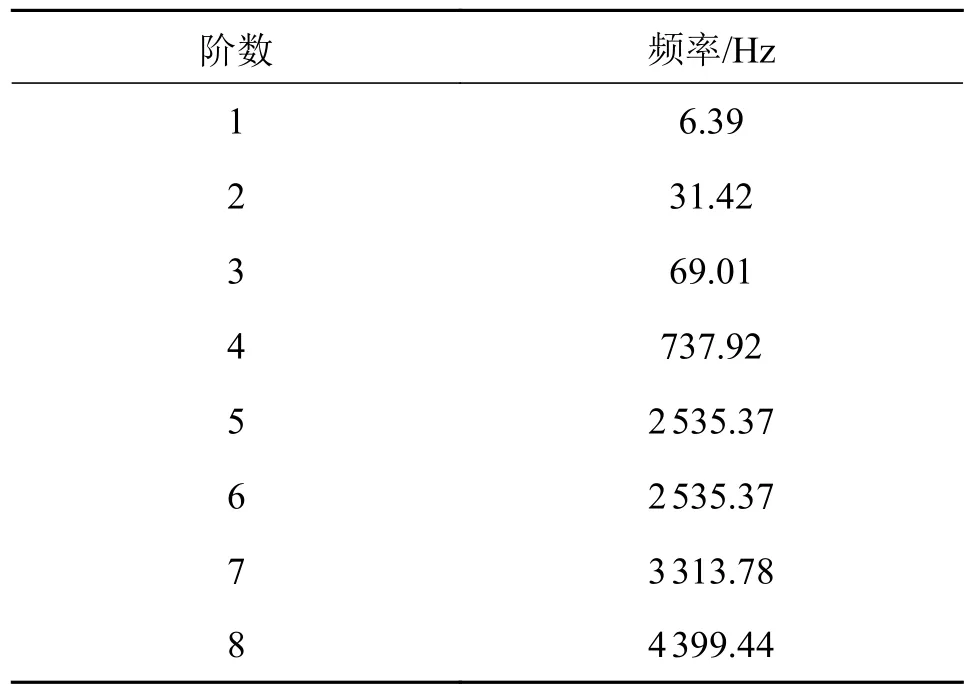
表4 混动中低速工况传动系统固有频率Tab.4 Natural frequency of hybrid medium and low speed transmission system

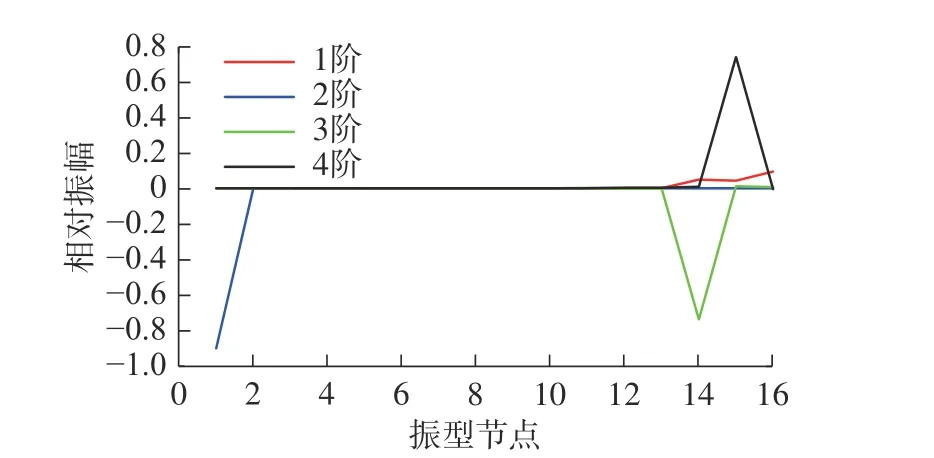
图10 混动中低速工况1 ～ 4 阶振型图Fig.10 1-4th order vibration modes of hybrid medium and low speed operating conditions

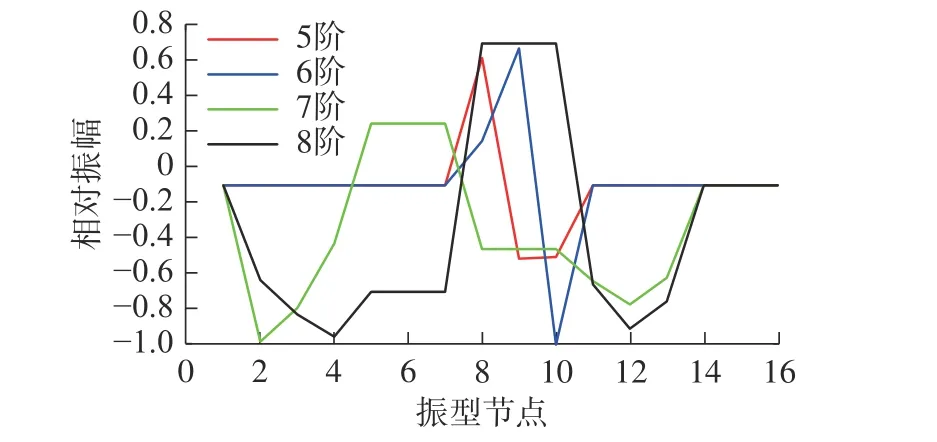
图11 混动中低速工况5 ～ 8 阶振型图Fig.11 5-8th order vibration modes of hybrid medium and low speed operating conditions

从图10 和图11 中可以看出：混动中低速工况1 ～ 4 阶频率下，发动机和左右车轮的振动较大；5 ～ 8 阶频率下，行星架、大太阳轮、短行星齿轮、长行星齿轮和减速器振动较大。

2.3 混动高速巡航工况传动系统固有特性

在高速工况下，发动机转速较高，可以实现较好的燃油经济性，此时将电机E1 锁死，不给电机E1 充电，发动机和大电机E2 共同驱动车轮。该工况为15 自由度振动模型，各阶固有频率如表5 所示。

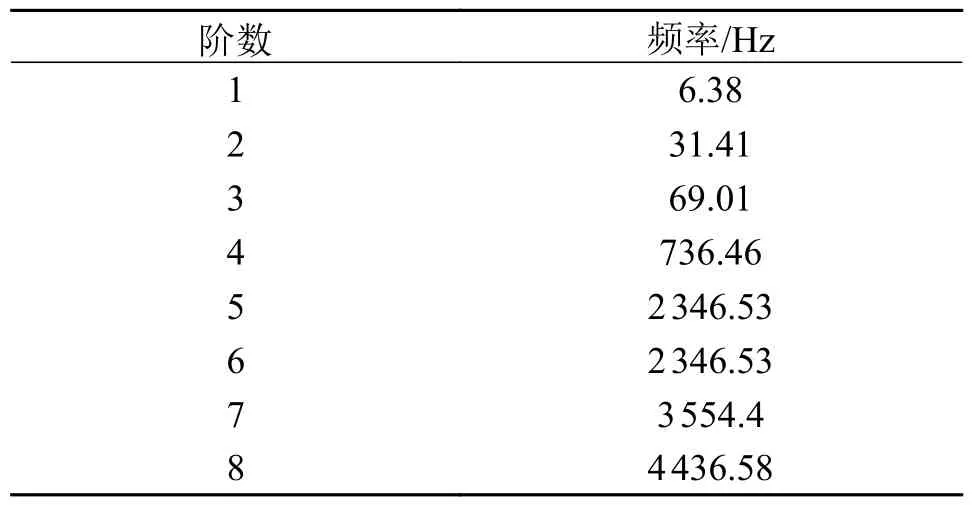
表5 电动工况传动系统固有频率Tab.5 Natural frequency of electric working condition transmission system

图12 和图13 分别为混动高速巡航工作模式1 ～ 4 阶和5 ～ 8 阶的振型图。从图12 和图13 可以看出：混动高速巡航工况1 ～ 4 阶频率下与中低速工况相似，发动机、左右车轮的振动较大；5 ～ 8 阶频率下，发动机、行星架、短行星齿轮、长行星齿轮和减速器振动较大，此外齿圈和差速器的振幅也较大。

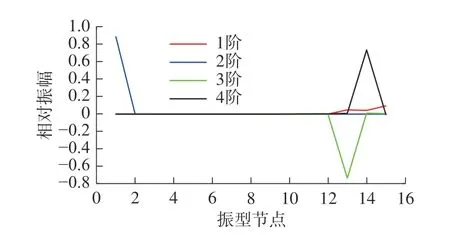
图12 混动高速巡航工作模式1 ～ 4 阶振型图Fig.12 1-4th order vibration modes of hybrid high-speed cruise operation mode

图13 混动高速巡航工作模式5 ～ 8 阶振型图Fig.13 5-8th order vibration modes of hybrid high-speed cruise operation mode

3 共振转速及其影响参数分析

当发动机与电机的激振频率和传动系统的固有频率相近时，便会发生共振。共振时振幅大幅度增大，会对整个系统造成非常严重的影响[16]。因此对传动系统共振转速进行分析具有重要意义。

3.1 电机共振转速分析

在纯电动工况下，电机提供动力，其激振频率和磁极对数有关。本文采用的PMSM 电机的磁极对数为6，所对应的激振频率为阶次6 的倍数。纯电动工况传动系统1 阶固有频率过小，4 阶以上太大。因此主要求解电机6 阶激振频率与传动系统2、3 阶固有频率的共振转速关系，如图14 所示。

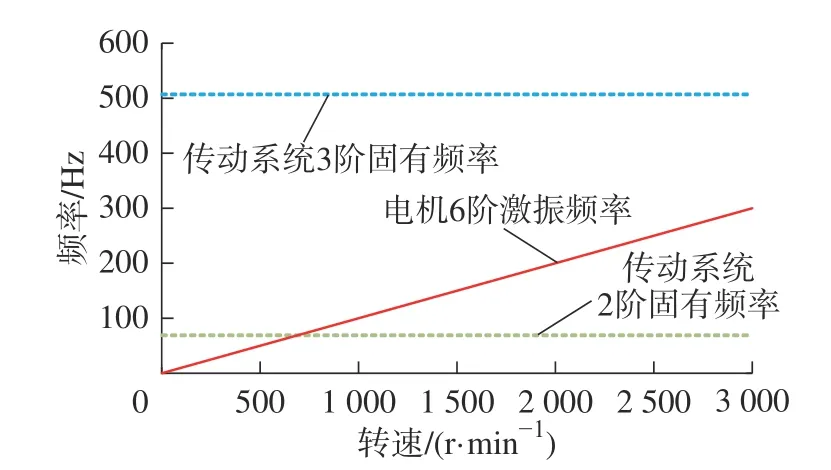
图14 电机的共振转速Fig.14 Resonance speed of the motor

电机工作平稳，激振波动小，产生的振动幅度较小。但同时电机的启动速度快，会在极短的时间内在共振转速区域，引起的瞬态冲击较大，因此与电机连接的部件应具有一定的抗瞬态冲击能力。同时电机工作转速较高，高频噪声明显，影响乘坐舒适性，在设计时要引起注意。

3.2 发动机共振转速分析

在混合动力驱动工况下，本文研究的四缸发动机，主谐量振幅会随着阶数迅速减小。因此选取发动机2 阶激振与传动系统2、3 阶固有频率的共振转速进行分析，如图15 所示。

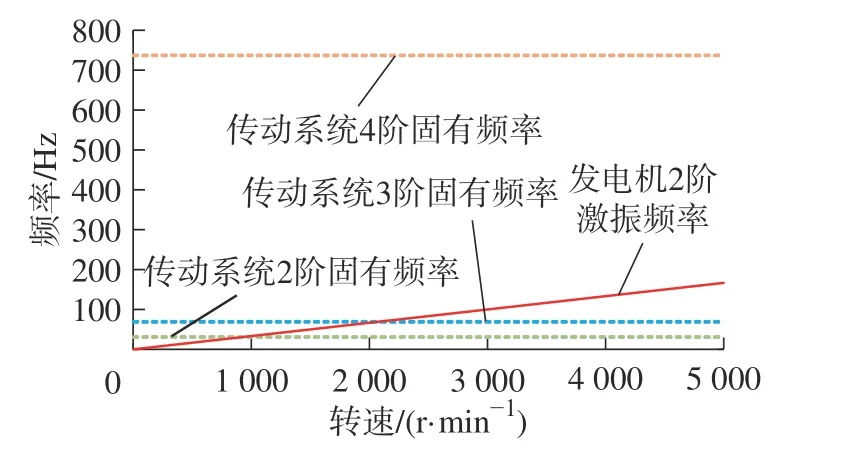
图15 发动机共振转速图Fig.15 Resonance speed of the engine

从图15 中可以看出传动系统4 阶固有频率较大，共振转速偏离发动机正常工作转速。发动机2 阶激振与传动系统2、3 阶固有频率的交点大于发动机怠速转速，位于发动机常用工作区内，存在共振风险。

3.3 传动系统共振转速影响规律分析

混动中低速和高速巡航工况下，传动系统前8 阶振动幅度较大的是：2 阶频率下发动机振动、3 阶和4 阶频率下驱动轮振动、5 阶和6 阶频率下长行星齿轮振动、7 阶和8 阶频率下长短行星齿轮振动。为了降低振动，下面分别研究飞轮等效转动惯量、车轮转动惯量、减振器刚度对各阶频率振动峰值的影响规律。将各参数在原数据的基础上进行等比例增减，分别选取-60%、-40%、-20%、20%、40%、60%，通过仿真分析得出不同参数对振动峰值的影响。

3.3.1 飞轮转动惯量影响分析

飞轮等效转动惯量与2 阶振幅变化如图16 所示，随着飞轮转动惯量的增大，2 阶发动机振动明显降低，其他阶次的振型基本不变。

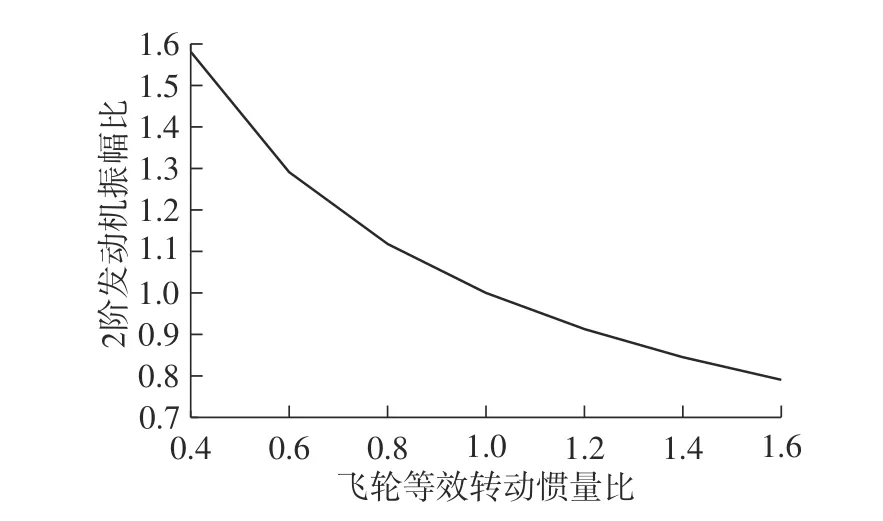
图16 飞轮等效转动惯量与2 阶振幅变化曲线Fig.16 Equivalent moment of inertia of flywheel and second order amplitude variation curve

3.3.2 车轮转动惯量影响分析

车轮转动惯量与3 阶振幅变化如图17 所示，随着车轮转动惯量的增加， 3 阶驱动轮振动幅度明显降低，同时5 阶和6 阶振动造成了影响但是变化规律不明显。

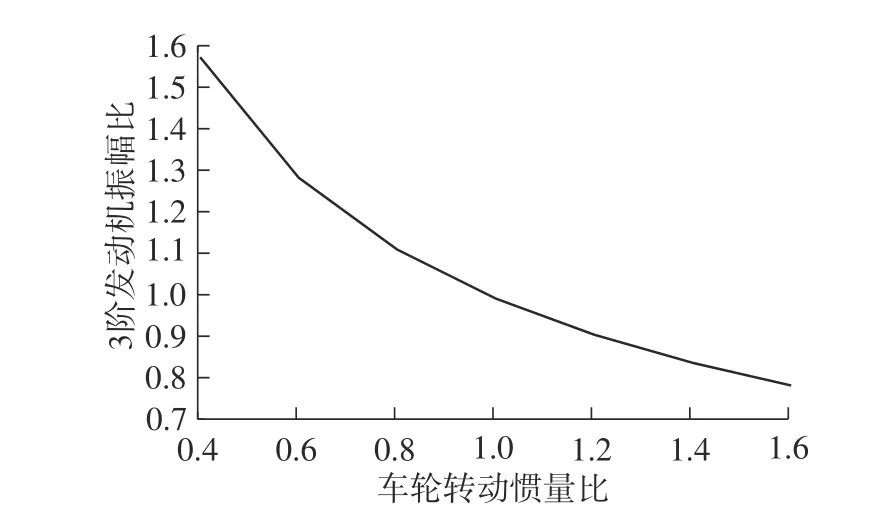
图17 车轮转动惯量与3 阶振幅变化曲线Fig.17 Wheel moment of inertia and third order amplitude variation curve

3.3.3 扭转减振器刚度影响分析

扭转减振器刚度变化对传动系统振动峰值的影响不大，但对传动系统2 阶固有频率影响较大，扭转减振器刚度对2 阶固有频率影响如图18 所示。随着扭转减振器刚度增大，传动系统2 阶固有频率逐渐增大。

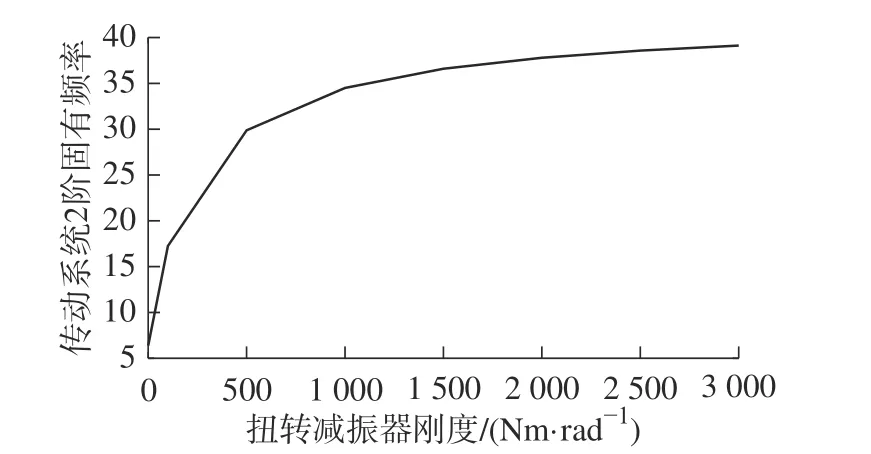
图18 扭转减振器刚度对2 阶固有频率影响曲线Fig.18 Influence curve of torsional shock absorber stiffness on second order natural frequency

3.4 扭转减振器刚度匹配

通过对传动系统参数影响规律分析，可以看出扭转减振器的刚度主要影响传动系统2 阶固有频率。对传动系统2 阶共振转速与扭转减振器刚度进行分析，得到发动机共振转速与扭转减振器刚度的关系，如图19 所示。

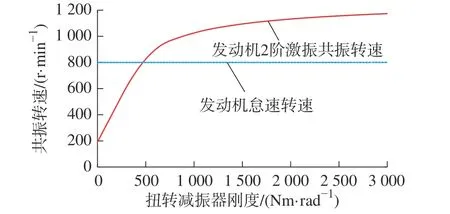
图19 扭转减速器刚度与发动机共振转速关系曲线Fig.19 Relationship curve between torsional reducer stiffness and engine resonance speed

从图19 可知：发动机2 阶激振共振转速与发动机怠速转速的交点处扭转减振器刚度为484 Nm/rad。为避开发动机常用工作区，建议扭转减振器刚度选择484 Nm/rad 以下。同时混合动力汽车发动机可实现大电机拖拽启动，所以其怠速转速比传统汽车高，有利于避开共振区，避免扭转减振器刚度较小。

4 结束语

以某款混合动力汽车为研究对象，通过推导功率分流装置的拉格朗日方程，建立其动力学模型，并采用Weber 能量法计算齿轮啮合刚度。在混合动力汽车传动系统其他部件模型适度简化的基础上，最终建立整车传动系统动力学模型。

针对不同运行工况，对传动系统固有特性进行了分析。纯电动工况低频段主要是驱动轮振动较大；高频段主要是复合行星齿轮排的行星轮振动较为突出。混动中低速工况和高速巡航工况较为相似，发动机和电机共同驱动使得传动系统扭转振动问题更加严重，低频段主要表现为发动机和驱动轮振动较大；高频段与纯电动工况类似，主要是行星轮和太阳轮振动较大。通过对传动参数影响规律分析，增大飞轮和车轮的转动惯量可以降低传动系统振动。通过对扭转减振器刚度进行优化匹配，使得发动机的共振转速低于发动机怠速转速，避开了发动机的工作转速范围。