高速重载弧齿锥齿轮齿面多目标优化设计

任鸿飞，王三民，陈鹏，张旭阳，张全清

（西北工业大学 机电学院，西安 710072）

航空航天汽车等领域中，弧齿锥齿轮作为传动 系统的关键，对其承载能力、接触性能、动态特性和可靠性等方面有着严格的要求。随着现代机械不断朝着高功重比的方向发展，使系统中所传递的载荷增大，振动与噪声问题更为突出。齿轮运转过程中，引起振动噪声的重要因素为实际重合度和传动误差[1]。提高设计重合度直接改善着齿轮副的承传动误差与动力学行为，传动误差又作为传动系统的激励因素。因此，具有高重合度与低传动误差幅值的齿面设计将显著改善齿轮传动的平稳性与齿间的载荷分配，同时能够获得良好的动态特性、啮合特性和强度性能[2]。

传统弧齿锥齿轮齿面设计以“局部共轭原理”为基础，通过Gleason 调整卡与轮齿试切控制齿面的啮合性能。Litvin 教授独立于传统的设计方法，提出了“局部综合法”[3-4]，该方法能够弥补传统设计中无法预控啮合特性参数的不足，首先预置三个齿面2 阶接触参数，并由微分几何理论建立两曲面之间线接触（刀具齿面与被加工齿面）和点接触（两相互啮合的齿面）两种情况下的基本方程组，最终由大轮切齿调整参数反推至小轮切齿调整参数，通过这种方法设计的齿轮副能够有效地对齿面参考点处的1 阶和2 阶接触性能进行控制。方宗德教授及其团队为国内引进局部综合法，并在此基础上通过对可选加工参数进行优化，对弧齿锥齿轮啮合质量进行整体控制[5-6]。邓效忠等[7-9]结合TCA 和LTCA等技术，给出了提高弧齿锥齿轮重合度的设计方法，达到提高齿轮强度与传动系统减振降噪的目的。蔡香伟[10]提出了一种高阶传动误差的变性系数修正方法，通过数值仿真验证了高阶设计的传动误差能够显著改善齿轮副的强度性能与动态特性，侧面反映高阶设计的传动误差可提高齿轮副的设计重合度。牟彦铭等[11-14]结合ease-off 技术并基于齿长曲率修正进行目标齿面的设计，降低高阶传动误差波动幅值，有效改善齿轮副的载荷分布与啮合性能。苏进展等[15]证明了沿齿长方向进行接触路径设计能够提高重合度，避免轮齿过早发生边缘接触。

本文结合TCA、LTCA 等技术，基于局部综合法建立高重合度与低啮合转换处传动误差幅值的多目标优化设计模型，利用NSGA-II 算法优化3 个齿面2 阶接触参数得到Pareto 最优解集，并根据目标函数的重要程度选择相对合适的非劣解。最后以一对弧齿锥齿轮为例，通过数值仿真对比分析优化前后齿轮副啮合性能和强度性能等多项指标以验证优化结果的合理性，达到减振降噪的效果。

1 基本概念

1.1 设计重合度与实际重合度

由于在不考虑轮齿表面弹性变形（假设齿轮完全刚性）时，大小齿轮的齿面之间构成了一对局部共轭曲面，即点接触曲面，同时为保证齿轮副的正常运转，要求其在啮合过程中保持连续切触，因此这种点接触表征在齿面上是一种连续的点列，即接触路径。

实际的齿轮都是非刚性的，因此在实际工作过程中，轮齿不可避免地会出现加载变形问题，由弹性接触理论知某时刻受载后的接触点会发生凹陷，展成瞬时接触椭圆，接触路径最终将构成齿面接触印痕。齿轮副的设计（理论）重合度（Contact ratio）由式（1）定义。实际重合度定义为轮齿在承受载荷条件下，同时进行啮合的轮齿对数的平均值。

TC与TZ表现在传动误差曲线中如图1 所示，其中TZ=360◦/N1。

图1 抛物线型传动误差曲线Fig.1 Parabolic transmission error curve

1.2 设计传动误差与载荷分配系数

弧齿锥齿轮产生传动误差的主要因素包括齿面的准共轭特性，加载引起的变形、安装误差及加工误差等，其定义如下：小齿轮做匀速运动时，大齿轮实际啮合转角与理论啮合转角的之间差值，对其Taylor 2 阶展开便可得到抛物线型传动误差曲线，如图1，具体表达式为

式中：N1、N2分别为小、大轮齿数； ϕ1、ϕ2分别为小、大轮当前啮合转角； ϕ01、ϕ02分别为小、大轮初始啮合转角；为1 阶传动比导数。

齿轮副在A点进入啮合至B点退出啮合，M点代表着齿面设计参考点； ϕ1A、 ϕ1B和 ϕ1M分别代表着小轮相应时刻的啮合转角； δTE为啮合转换点处的传动误差幅值，其与1 阶传动比导数的关系为

联立式（2）和式（3），得到大小轮啮合转角得表达式为

基于此可对弧齿锥齿轮的传动误差进行预控，以满足所要求的啮合性能。

当齿轮副的实际重合度大于一时，多对轮齿将同时参与啮合并共同承受着载荷的作用，定义齿间载荷分配系数为

式中：pmax为该啮合瞬时轮齿上所承受的最大载荷；P为齿轮副所传递的总载荷。

1.3 轮齿几何接触分析与承载接触分析

为了更加直观地反映弧齿锥齿轮副的啮合特性，通常采用轮齿几何接触分析（Tooth contact analysis，TCA）技术模拟齿轮副的啮合过程。首先基于局部综合法，由大轮的切齿调整参数反推出小轮的切齿调整参数，从而获得大小轮齿面方程，同时为保证齿面每一啮合瞬时始终连续切触，得TCA 基本方程为：

式中：下标h表示各矢量位于啮合坐标系Sh中；θF,ϕF和 θG,ϕG分别为小轮和大轮齿面的曲面坐标参数； ϕ1和 ϕ2分别为小轮和大轮的啮合转角。

由于TCA 技术假设轮齿为完全刚性，且未考虑负载的作用，从纯数学的角度阐述齿轮副的啮合过程，因此分析结果一般仅用于评价初始设计参数对应的齿面质量，与实际承载运转时的情况大相径庭。轮齿承载接触分析（Load tooth contact analysis，LTCA）技术考虑了齿轮副实际工作时产生的加载变形以及载荷分配对于齿轮啮合特性的影响，基于TCA 技术、有限元法、柔度矩阵法以及数学规划法建立的LTCA 基本方程为：

式中：F为n×n柔 度矩阵，n为当前啮合瞬时可能发生接触的离散点总数；p为n维 载荷向量； ω维n初始间隙向量； Θ为弹性变形引起的大轮转角；r1和r2分别为n维小轮和大轮接触点的回转半径向量；d为n维弹性变形后的间隙向量；T1为输入扭矩。

2 优化策略

在计算Pareto 解集时由于NSGA-II 算法（带精英策略非支配排序遗传算法）的精确度高、分散性好，故本文拟采用该算法实现弧齿锥齿轮齿面多目标优化。

2.1 多目标优化问题

针对多目标优化问题（Multiobjective Optimization Problems，MOPs），需要对多个目标同时进行最优化，这些目标之间可以是相互矛盾的，因此难以甚至无法找到一种解使各目标函数均达到最优，即任何两种解不一定能够比较出之间的优劣，将这类解称为非劣解（Pareto 最优解），将所有的Pareto 最优解组合起来构成Pareto 最优解集[16]。因此根据具体的多目标问题的设计要求和实际经验，从Pareto 最优解集中选择相对合理的解作为最终优化结果，是解决多目标优化问题的重要目标。

2.2 NSGA-II 算法

解决多目标优化问题的遗传算法众多，其中具有代表性的诸如小生镜Pareto 遗传算法（Niched pareto genetic algorithm，NPGA）、非劣解排序遗传算 法（ Non-dominated sorting genetic algorithms，NSGA）等，其中虽然NSGA 算法广泛应用于众多工程实际问题上，但仍存在不足[17]，NSGA-II 对NSGA去粗取精，使得该算法应用于实际工程问题中效果显著。故拟采用该算法求解本文齿面多目标优化问题，其算法主流程[18]如图2 所示。

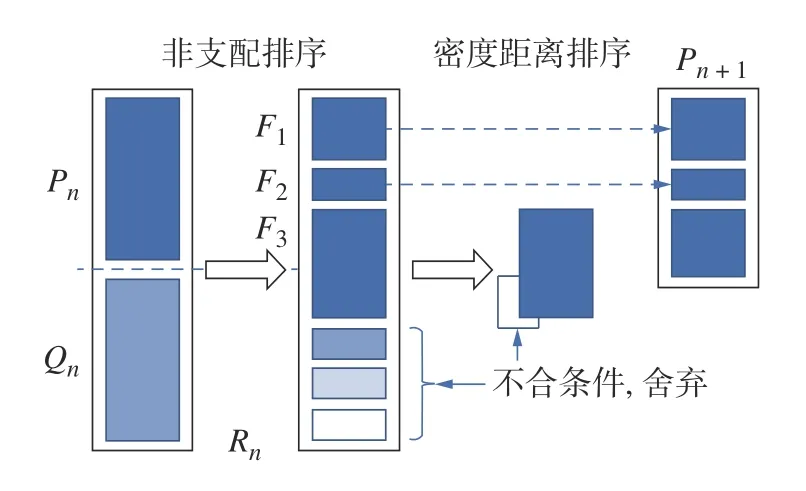
图2 NSGA-II 流程Fig.2 Flowchart of NSGA-II

2.3 高速重载弧齿锥齿轮的齿面优化设计数学模型

由于弧齿锥齿轮的重合度和转换处传动误差幅值主要受到2 阶接触参数的影响，且3 个2 阶接触参数之间相互独立，因此基于基于局部综合法与TCA、LTCA 技术，设计出具有高重合度且低啮合转换处幅值的齿面，建立如下多目标优化设计模型。

优化变量

目标函数

约束条件

3 数值算例与分析

3.1 数值算例

以某弧齿锥齿轮副为例进行齿面多目标优化设计，齿轮坯的基本参数见表1。NSGA-II 算法所涉及部分参数设置见表2，在进行500 代进化后得到Pareto 最优解集，并通过均匀采样，最终获得弧齿锥齿轮齿面多目标优化问题的Pareto 近似前沿，见图3。对双目标进行无量纲化处理并根据优化目标的重要程度，选择重合度权重因子为0.7，啮合转换处传动误差幅值权重因子为0.3，获得最终优化结果。优化前后2 阶接触参数列于表3，优化前后目标函数计算结果列于表4。

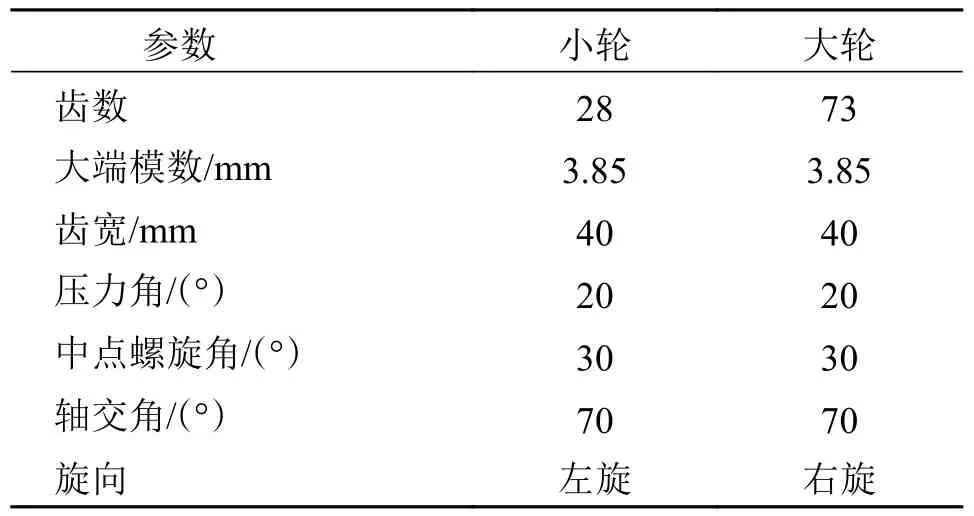
表1 齿轮坯基本参数Tab.1 Basic parameters of gear blank

表2 NSGA-II 相关参数设置Tab.2 NSGA-II related parameter setting

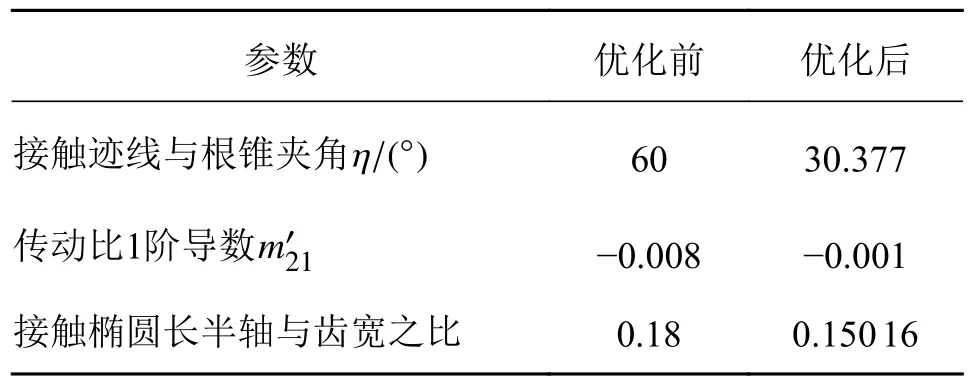
表3 优化前后2 阶接触参数Tab.3 Second-order contact parameters before and after optimization

表4 优化前后目标函数计算结果Tab.4 Calculation results of objective function before and after optimization

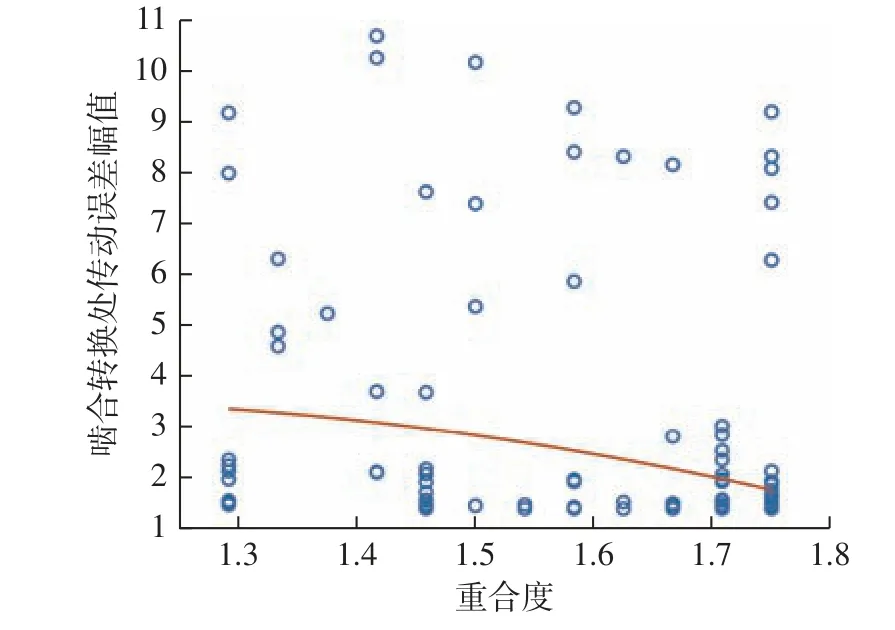
图3 Pareto 近似前沿Fig.3 Pareto approximate frontier

3.2 啮合性能分析

基于TCA 技术获得优化前后对应的大小轮齿面印痕和及传动误差曲线，见图4 和图5。

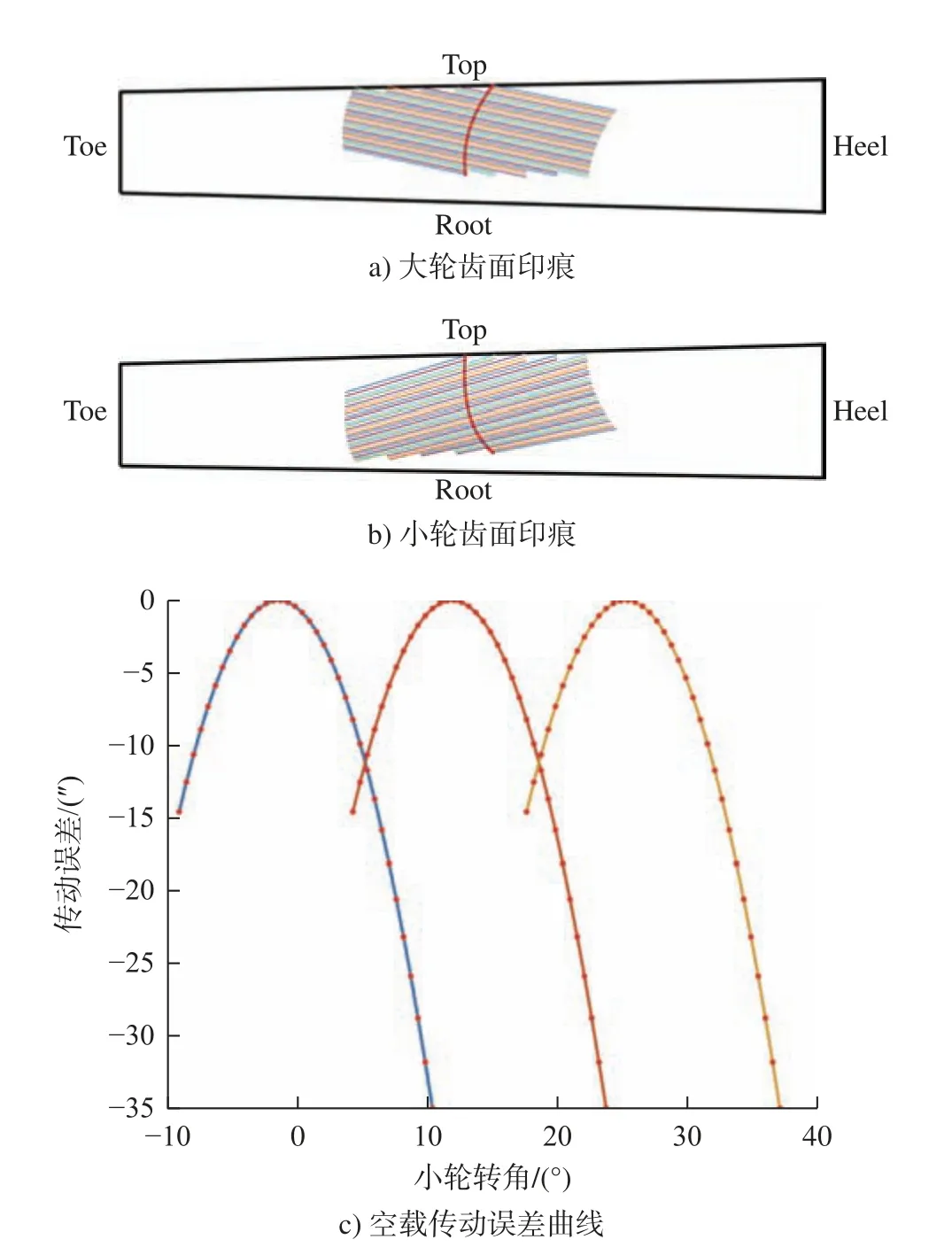
图4 优化前2 阶参数对应的TCA 结果Fig.4 TCA results corresponding to the second-order parameters before optimization

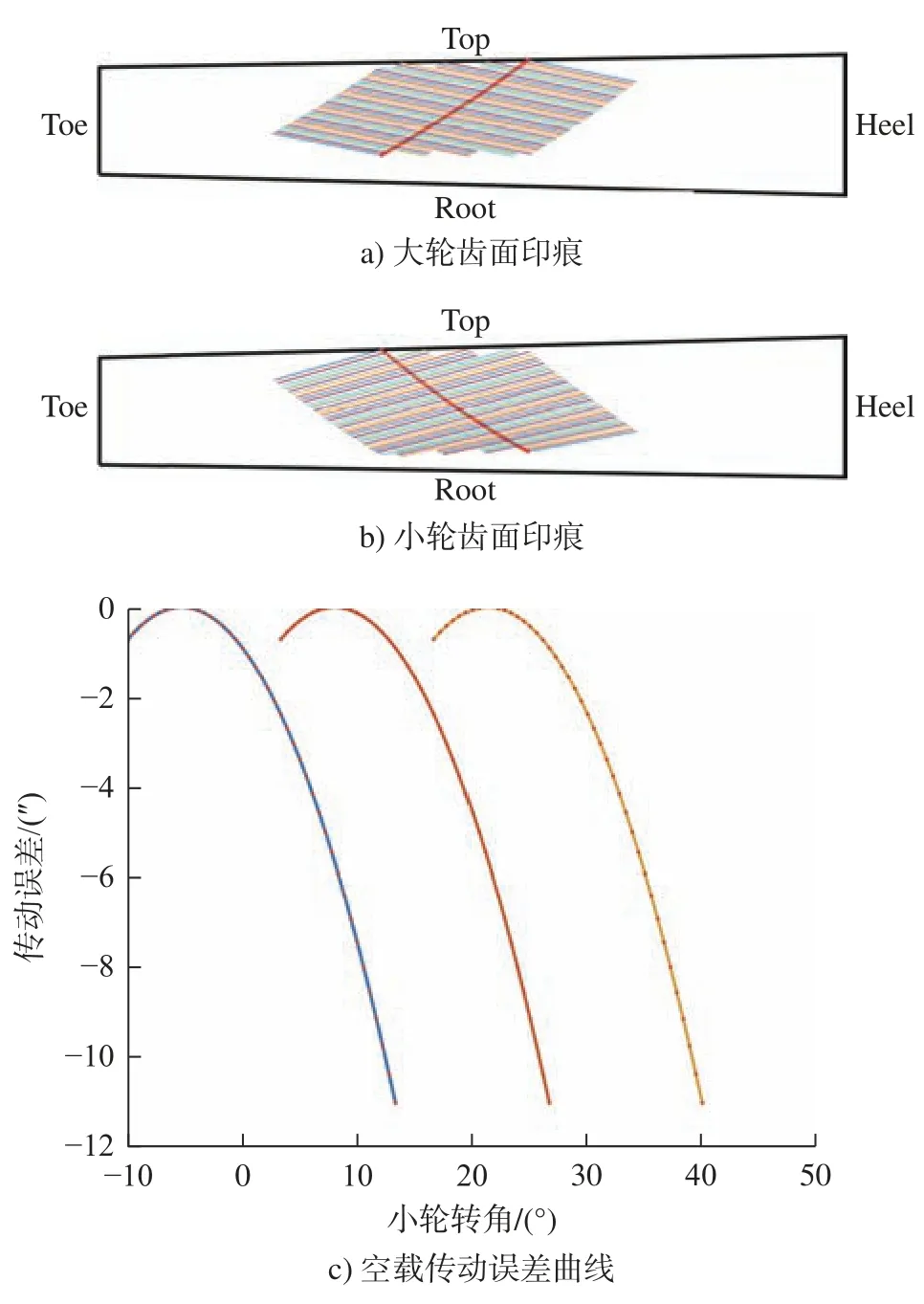
图5 优化后2 阶参数对应的TCA 结果Fig.5 TCA results corresponding to the second-order parameters after optimization

由图4、图5 和表4 可以看出：对比优化前后的齿面接触印痕，不难发现齿面啮合区域面积和啮合点的个数明显增加，接触迹线倾斜程度提高，且更加趋于直线；重合度对大轮凸面接触迹线与大轮根锥夹角的变化非常敏感，降低其夹角的大小，重合度明显增加，优化后的重合度相较优化前增加了16.69%；啮合转换处传动误差幅值对于1 阶传动比导数的变化及其敏感，优化后的幅值相较优化前降低了87.33%；大轮凸面接触椭圆长轴半径与齿宽比对于重合度与啮合转换处传动误差幅值的影响较小。

为进一步对比验证优化后的啮合特性，基于LTCA 技术，计算得到优化前后承载传动误差曲线、齿面接触应力分布曲线、齿间载荷分配系数曲线以及大小轮齿根弯曲应力曲线如图6 与图7 所示。

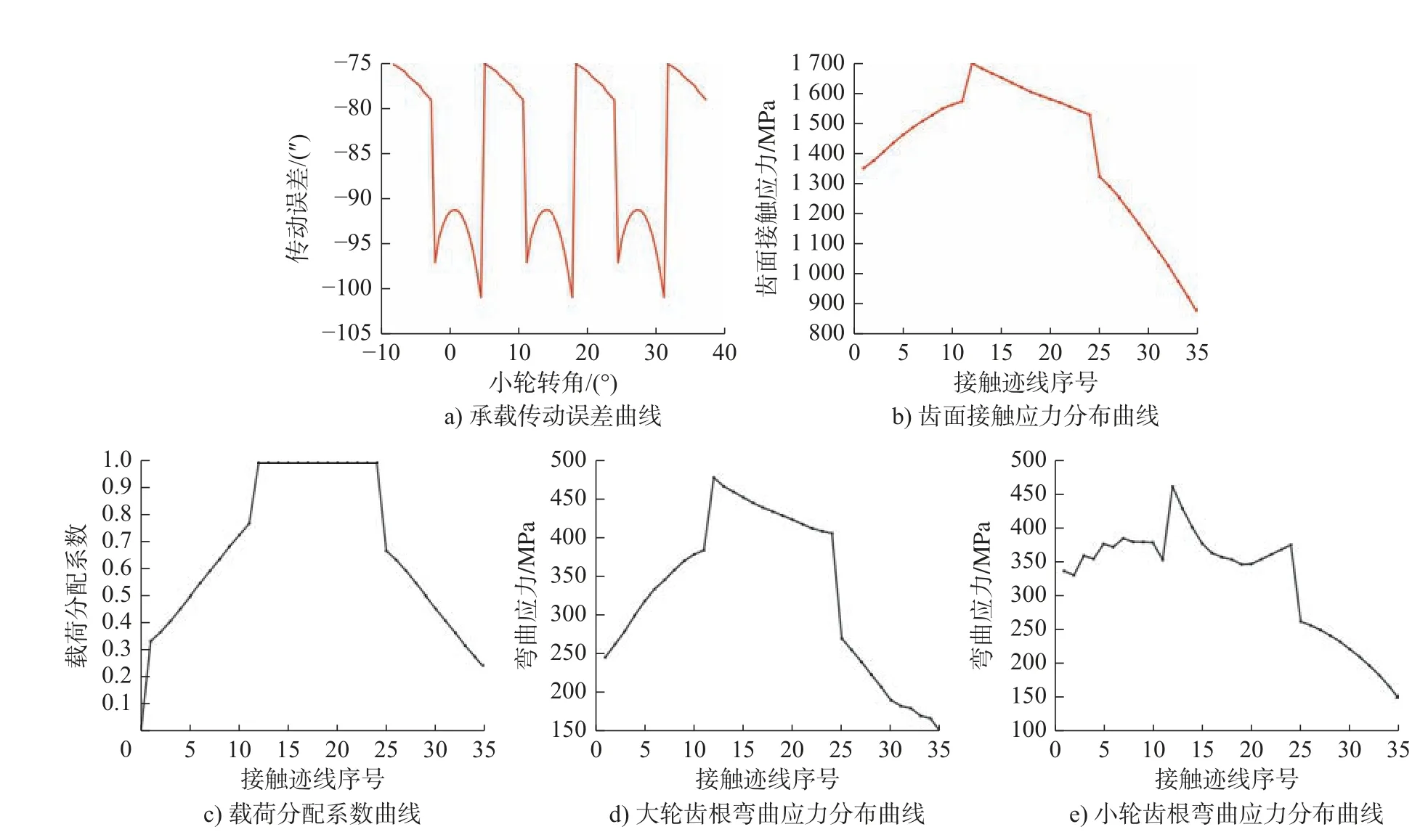
图6 优化前2 阶参数对应的LTCA 结果Fig.6 LTCA results corresponding to the second-order parameters before optimization

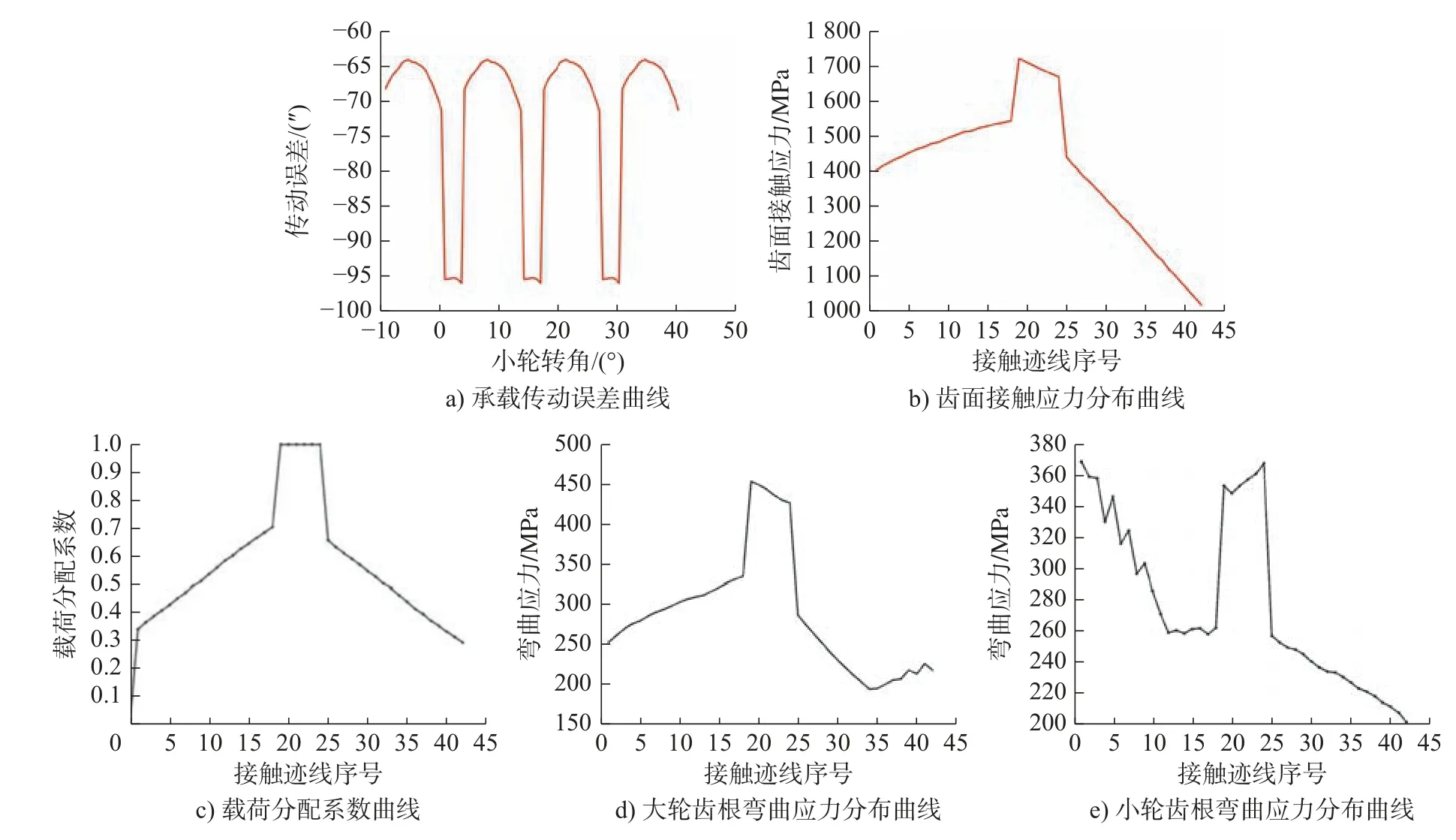
图7 优化后2 阶参数对应的LTCA 结果Fig.7 LTCA results corresponding to the second-order parameters after optimization

对比图6c)和图7c)，优化后的齿面由于设计重合度的提高，单齿的啮合周期显著增加，且一个啮合周期内单齿承受满载的比例大幅降低。为便于后续说明，将图6 和图7 中涉及的具体数值信息列于表5。根据图6、图7 和表5 得出：优化后承载传动误差整体减小，且在一个啮合周期内突变次数减小，有利于齿轮副的平稳运转，改善其动态特性；优化后齿面接触应力均值和大小轮齿根弯曲应力均值均得到不同程度的减小，其中弯曲应力降低幅度最大，优化后的齿面具有良好的啮合特性，且接触强度和弯曲强度均有所提高。

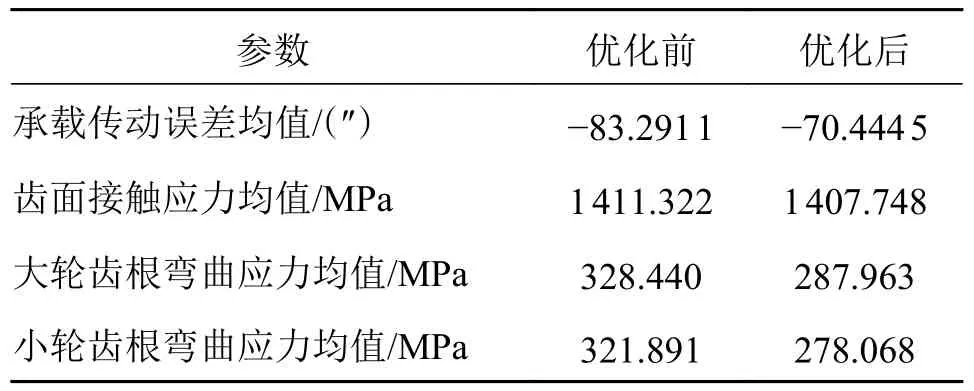
表5 优化前后各接触特征响应Tab.5 Contact characteristics response before and afteroptimization

4 结论

利用局部综合法、TCA 技术等提出两个目标函数与3 个设计变量，并合理设置约束条件，基于NSGA-II 算法实现弧齿锥齿轮多目标优化，并结合LTCA 技术模拟真实齿面接触过程。得出如下结论：

1）对比优化前后的齿面接触印痕，齿面啮合区域面积、啮合点的个数及接触迹线倾斜程度均有所增加，且接触迹线向直线逼近。

2）对比优化前重合度为1.458，啮合转换处传动误差幅值为11.130″，优化后重合度增加了16.69%，幅值降低了87.33%，具体数值分别为1.75 和1.410″。

3）对比优化前后各接触特征响应，优化后的承载传动误差均值、齿面接触应力均值与大小轮齿根弯曲应力均值分别下降了11.82%、0.25%、12.32%和13.61%，且一个啮合周期单齿承受满载的比例大幅降低，齿面接触性能和强度整体得到提升。