无人车辆横向跟踪控制研究

李伯雄，王立勇，孙鹏，季文龙

（1.北京信息科技大学 现代测控技术教育部重点实验室，北京 100192；2.中国人民解放军 63966 部队，北京 100072）

无人车辆的轨迹跟踪控制算法在实际车辆控制系统中将决策层与硬件层相结合，对车辆轨迹跟踪起到重要作用。通过提高无人车辆在未知路面对决策轨迹的跟踪效果，可提高车辆追踪决策轨迹的准确性及高效性。轨迹跟踪控制算法的研究主要使用模型预测控制器（MPC）[1]进行搭建。

MPC 通过引入滚动优化及反馈校正，实现对系统状态的预测，进一步提高车辆运动轨迹的控制稳定性。李想等[2]提出一种变权重的模型预测控制算法，针对不同车速进行权值再分配，从而实现兼顾不同目标跟踪速度下的高精度控制。何德峰等[3]提出通过控制增量分层的策略以降低系统运算量，在保证追踪性能的前提下加快系统运算速度。

车辆行驶过程中的状态变化与路面条件关系紧密，因此诸多学者借助车载传感器对路面信息进行准确辨识。张航星等[4]使用扩展卡尔曼滤波对车辆的轮胎力进行观测，从而预测路面附着系数。刘志强等[5]使用自适应衰减卡尔曼滤波（AFUKF）对四轮路面附着系数进行估测，并使用Sage-Husa 噪声估计器提高了预测模型的准确性，但未对转向工况进行分析。另一些研究者则着重提高在未知路面条件下车辆的控制性能及安全性能。李绪龙等[6]提出一种双重无迹卡尔曼算法，将预测得到的路面附着系数反映到车辆纵向控制算法中，修正刹车距离与安全跟车距离，降低汽车发生碰撞的可能性。未对弯道工况进行控制优化。杨秀建等[7]针对低附着系数工况，使用最小二乘法对路面附着系数进行实时预估，通过预测结果的反馈改变安全距离约束，确保车辆控制的可靠性。但对于高附着系数工况的路面估计存在较大偏差。

实际车辆行驶过程中，路面附着系数难以通过传感器直接获取，因此本文提出的横向跟踪控制算法结合实车装配的四轮转速及转角传感器，读取状态信息，通过具有算法稳定性的扩展卡尔曼滤波器进行附着系数预测。再根据车辆当前控制量与位姿状态，对控制模型中的侧偏角约束进行调整，优化车辆在未知路面下的横向跟踪控制效果。

1 轨迹跟踪车辆动力学模型

1.1 车辆动力学模型

Carsim 中无人车辆模型主要参数见表1。

本文研究的轨迹跟踪控制模型是基于四自由度动力学模型构建的。该模型可以在车辆转向时分析四轮横纵向受力、转速及车辆横摆角速度等运动性能，如图1 所示。

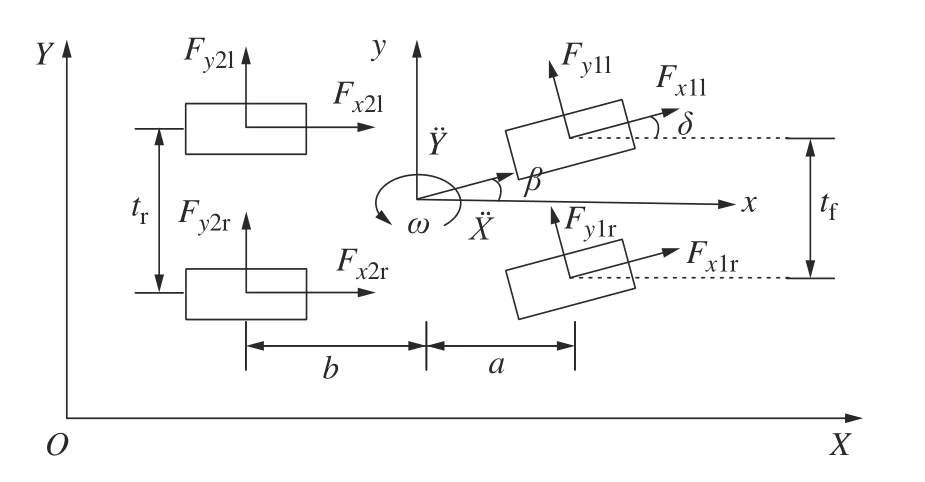
图1 四自由度车辆动力学模型Fig.1 Four degree of freedom vehicle's dynamics model

车辆在路面行驶过程中，沿x、y及z轴（横摆）方向受力平衡，由此得出车辆纵向、侧向及横摆方向微分方程。

纵向运动方程为：

侧向运动方程为：

横摆方向运动方程为

车辆在惯性坐标系OXY中的平面运动方程：

1.2 路面附着系数预测模型

根据Dugoff 模型[8]，对路面附着系数与车轮所受的纵向力、横向力的关系进行描述，建立归一化横纵向力的表达式，即：

其中：

联立式（8）和式（9）及式（2），式（4）和式（5）得到整车四轮的非线性动力学微分方程，即：

2 变侧偏角约束控制器设计

2.1 路面附着系数预估方法

1）建立系统状态方程

2）建立测量方程

式 中：4 个 轮 胎 路 面 附 着 数xk= [µ1,µ2,µ3,µ4]T；A=I4∗4； 过 程 噪 声wk= 0.01I4∗4； 测 量 变 量yk=[ax,ay,ω˙]T；控制输入量uk=[δ] ；观测噪声vk=I4∗4。

Hk为测量方程yk对xk求偏导数，将模型线性化得到的雅各比矩阵。

其中：

3）创建EKF 系统噪声

式中：Q为过程噪声协方差矩阵；x-0为参数变量初始数值；R为观测噪声协方差矩阵；P-(t0)为初始协方差矩阵。

4）设定系统误差初值

5）定义状态预测量xˆk¯=f(xk-1,0)及状态协方差Pk¯=Pk-1+Q。

6）更新校正状态方程

误差协方差矩阵为

7） 通过每一时刻的状态，重复5）和6）进行运算。

2.2 建立变约束线性时变模型

本文重点研究提高轨迹跟踪效果，不涉及具有不确定性的突发情况，因此预测控制模型选用线性时变模型预测控制器[9]。首先对式（1）～ 式（5）进行线性化处理，得到线性时变方程，即

式中：系统状态量 ξ=[x˙,y˙,ω,ω˙,X,Y]T；系统控制量u(t)=[δ]；A(t)=∂f(ξ)/∂ξ，B(t)=∂f(ξ)/∂u。

使用1 阶差商法对式（18）进行离散化，结合离散状态量x(k) 和 控制量u(k)构成离散的状态空间表达式为：

式中：A˜(k)=I+TA(t) ，B˜(k)=T B(t)，T为采样周期。

2.3 侧偏角约束设定

通过对质心侧偏角添加软约束，实现未知路面附着系数工况下，车辆稳定性的进一步提升。通过文献[10]所描述，使用相平面法分析得出：随路面附着系数减小，能够支持车辆稳定行驶的最大质心侧偏角随之减小。当在车辆处于不同路面附着系数工况行驶时，质心侧偏角稳定区域的边界条件为

式中： µ为路面附着系数；g为万有引力常数。

在调试过程中，以式（21）为理论依据，对不同路面附着系数下质心侧偏角进行约束，当 µ分别取0.2、0.5、0.85 时，质心侧偏角 |β|软约束取值分别设定为：2.2°、5.5°和9.4°。

为确保在控制车辆轨迹跟踪过程中车辆的姿态稳定性、跟踪效果稳定性、控制算法稳定性，算法在求解阶段对每次循环中的控制量进行约束。

式中:J(ξ(t)) 为 输出量和期待输出量的差值；u(t-1)为上一时刻控制量； ∆U(t)为上一控制时域与当前控制时域控制量的差值；yh为系统输出硬约束，包括最大前轮转角、最大车速、最大加速度；ys为系统输出软约束，包括横向加速度约束、侧偏角约束。

2.4 侧偏角约束自适应调节

为实现对路面附着系数的实时响应及侧偏角约束的实时调整。结合扩展卡尔曼预测结果，选用拟合曲线方式进行侧偏角约束调节，如表2 所示。

表2 侧偏角与路面附着系数对应关系Tab.2 Lateral deviation angle and road adhesion coefficient correspondence

借助MATLAB/Simulink 中Cftool 工具对实际曲线进行拟合获得

式（23）将实时变化的路面附着系数转换为侧偏角约束量，对横向跟踪控制算法进行约束。

3 仿真分析

3.1 路面附着系数预测

联合CarSim 和Simulink 分别对路面附着系数分别为0.20，0.50，0.85 的72 km/h 双移线工况进行仿真分析，结果如图2 所示。

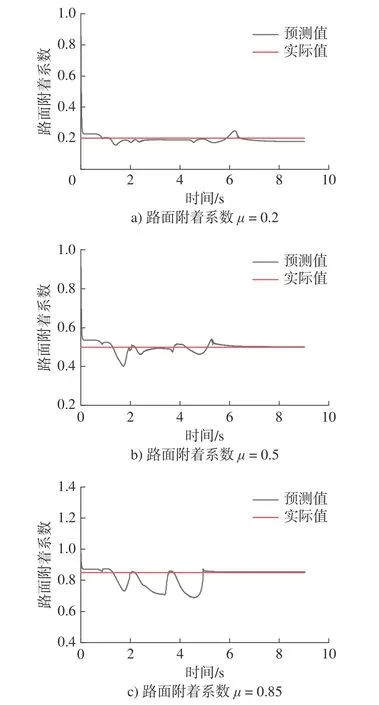
图2 扩展卡尔曼预测结果Fig.2 Extended Kalman prediction results of road adhesion coefficient

在路面附着系数 µ= 0.2 的工况下，0.8 s 时预测值初次达到实际路面附着系数值，在完成当前工况行驶的9 s 内， µ平均值为0.193，均方根误差值为0.019，相对平均偏差7.59%。

在 µ=0.5 工况下，1.2 s 时预测值初次达到实际值，在完成当前工况行驶的9 s 内， µ平均值为0.499，均方根误差值为0.024，相对平均偏差3.46%。

在 µ=0.85 工况下，1.4 s 时预测值初次达到实际值，在完成当前工况行驶的9 s 内， µ平均值为0.821，均方根误差值为0.065，相对平均偏差6.07%。

3 种路面工况下平均值误差在3.5%以内，均可以为控制算法提供可靠的路面附着系数值。

3.2 横向跟踪控制仿真

本文仿真车辆以72 km/h 的纵向速度，在µ=0.2、 µ=0.5、 µ=0.85 的双移线工况[11]下行驶。联合Carsim 与Simulink 进行仿真，Carsim 选用2020版本MATLAB/Simulink 选用R2020a 版本。Carsim提供车辆的实时位姿及状态信息，Simulink 环境下搭建路面附着系数预测算法及模型预测控制器。横向跟踪控制算法结构如图3 所示。

图3 横向跟踪控制算法结构Fig.3 Structure of lateral tracking control algorithm

通过对比横向追踪参考值与仿真值对控制效果进行评价[12]，过程如下：

1）创建双移线轨迹并将预测控制模型初始化。

2）应用线性时变的模型预测控制（LTV MPC）算法[13]，计算车辆前轮转角，输出至CarSim 车辆模型进行目标轨迹跟踪。

3）读取EKF 预测路面附着系数值[14]，调整LTV MPC 算法内侧偏角约束值，对车辆前轮转角进行预测控制。

4）重复过程2）和过程3），在每个程序循环中对未来时域的车辆状态进行预测，将最优控制量输出至车辆模型。

仿真结果表明：

1）当 µ=0.2 时，车辆经过第一个弯道后，常规算法控制的车辆由于缺少质心侧偏角软约束，此时车辆质心侧偏角达到11°，在方向盘转角达到最大时仍无法控制车辆回正，导致车辆处于失控状态[15]，如图4a)所示。同一工况下，改进控制算法通过路面附着系数反馈，提前对侧偏角软约束进行修正，将四轮侧偏角控制在0.8°以内。质心侧偏角在0.19°以内。在1.8 s 时控制车辆行驶回到初始横向位置，如图4b)和图4c)所示。

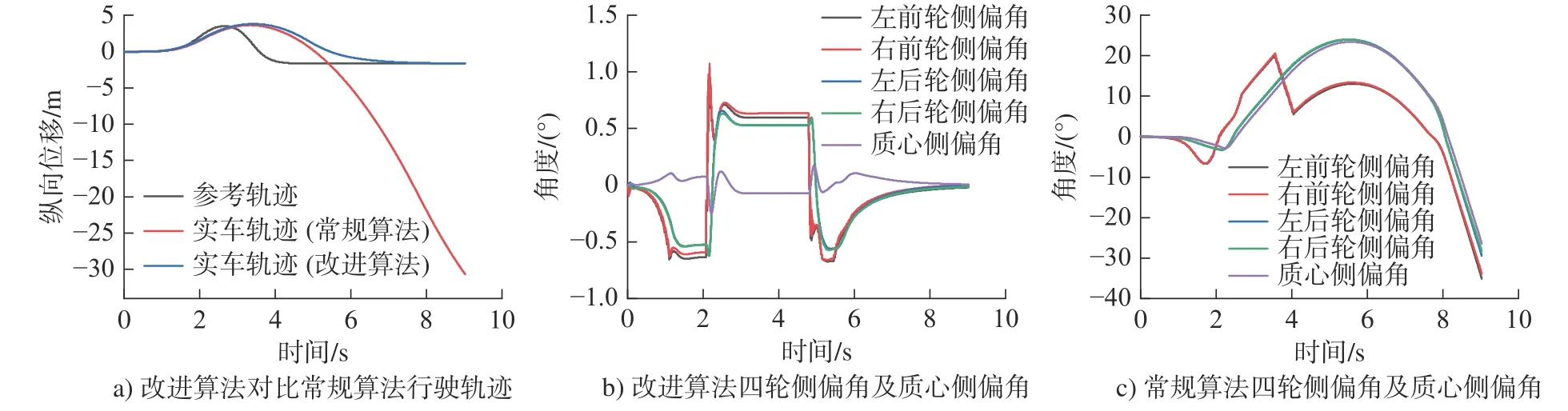
图4 附着系数μ = 0.20 的控制效果Fig.4 Control effect when the adhesion coefficient μ = 0.2

2）当 µ=0.5 时，常规算法控制车辆经过第一个弯道回正时出现横向位移偏差，在4.3 s 时回到初始横向位置，此时车辆位姿处于超调状态。第6 s 时，车辆处于纵向位移– 4.675 m 位置，此时质心侧偏角达到–14.6°，随后无法控制车辆回到规定轨迹上，车辆属于完全失控状态，如图5a)所示。经过改进的控制算法在减小横向位移偏差的同时，通过添加质心侧偏角软约束在回正过程中对转角进行调节，将四轮侧偏角约束在5°以内，使车辆在6.9 s 回到规定轨迹，如图5b)和图5c)所示。

图5 附着系数μ = 0.50 的控制效果Fig.5 Control effect when the adhesion coefficient μ = 0.50

3）当 µ= 0.85 时，常规算法与改进算法差别较小，如图6 所示）。观测此时质心侧偏角约束发挥作用。常规控制算法控制下的车辆四轮侧偏角最高7.8°，质心侧偏角最大值为3.8°，在4.8 s 时出现超调，导致车辆需要进行再次回正调整。优化算法所约束的四轮侧偏角均控制在4.2°以内，质心侧偏角保持在1°以内，未出现回正超调现象，确保车辆姿态的稳定。改进算法在2.64 s 跟踪参考轨迹达到纵向位移最大值，常规算法在2.7 s 跟踪参考轨迹达到 纵向位移最大值，控制效果优化2.2%。

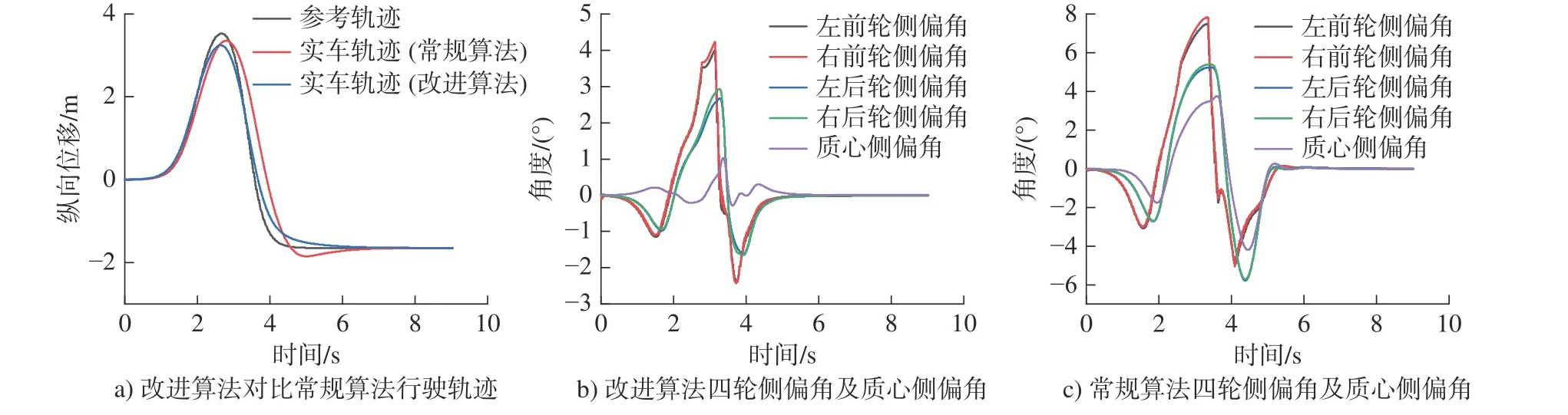
图6 附着系数μ = 0.85 的控制效果Fig.6 Control effect when the adhesion coefficient μ=0.85

因此证明在中低附着系数工况下，本文所使用的优化算法可以对纵向速度为72 km/h 的车辆进行更优控制，在高附着系数双移线的工况下，本文所使用的优化算法提高了车辆姿态的稳定性。

4 结论

1）由于道路受环境影响存在未知性，通过扩展卡尔曼滤波实时预测路面附着系数，将车辆所行驶路面状态融入控制算法，在横向控制部分进行应用，可增强车辆在不同路面横向轨迹跟踪的鲁棒性。

2）在低附着系数路面下，仿真实验结果表明，常规算法出现过大漂移，无法完成仿真测试。优化控制算法通过对附着系数预测后调整侧偏角约束，完成对低附湿滑工况的横向跟踪，提高车辆横向轨迹跟踪效果。

3）在高附着系数路面下，对车辆四轮侧偏角及质心侧偏角进行软约束，解决车辆在向右横向位移后产生超调的问题，提高横向跟踪控制效果2.2%，同时也提高了车辆自身姿态的稳定性。