基于光滑粒子流体动力学的波浪中航行体入水数值模拟

2024-03-18管祥善孙鹏楠李江昊孙龙泉

空气动力学学报 2024年2期

管祥善，孙鹏楠，2，*，李江昊，孙龙泉

(1. 中山大学海洋工程与技术学院，珠海 519000；2. 中国空气动力研究与发展中心结冰与防除冰重点实验室，绵阳 621000；3. 哈尔滨工程大学船舶工程学院，哈尔滨 150001)

0 引言

航行体在波浪中的入水问题一直是海洋工程中研究的热点和难点，航行体在波浪条件等复杂环境下入水的弹道稳定性，也一直是国防领域中十分关注的问题。航行体在波浪中的入水过程是一种非常复杂的流体力学现象，涉及到水动力学、空气动力学、刚体动力学等多个学科领域[1]。在高速航行体入水过程中，入水冲击载荷和运动响应会影响航行体的运动轨迹[2-3]，而波浪在自然界广泛存在且很难避免，波浪的相位、浪高、频率等物理参数呈现强随机性，也会对航行体的入水状态和运动轨迹产生明显的影响[4]，进而决定发射任务的成败[5]。研究真实波浪条件下航行体的入水过程可以更好地了解航行体在波浪中的运动规律以及波浪对于航行体运行轨迹的影响，可为海洋工程和国防领域航行体的设计和优化提供技术支撑，满足国家重大战略需求。

针对航行体的入水问题，主要采用理论研究[6-7]、试验研究[8-11]和数值模拟[12]。随着计算机技术的高速发展，数值模拟逐渐成为解决工程问题的主要方法，计算流体动力学（Computational Fluid Dynamics,CFD）逐渐成为水动力学研究的一种主要手段[13-15]。但是，由于航行体波浪入水问题中包含的复杂物理现象，对其进行准确数值仿真始终是CFD领域最具挑战性的课题之一。目前，大多数的CFD数值模拟方法是基于网格类方法[16-18]。杨晓光等[19]采用流体体积多相流模型和动网格技术建立高速入水数值模拟方法，并开展静水工况下航行体入水试验，验证了其数值方法的精度，并基于此数值方法对航行体在波浪条件下的高速斜入水过程进行模拟，得到了航行体在不同相位角下的入水轨迹和运动响应结果。尽管网格法可以精确计算航行体入水过程中的水动力载荷，但需要提前对飞溅区域进行网格加密处理才能精确地捕捉大变形液面和飞溅液滴。在模拟自由液面大变形运动时，拉格朗日粒子算法更具优势[20-22]，该算法易于处理大变形和快速移动的自由表面，以及飞溅的离散液滴，并能捕捉和生成多相流界面，无需额外的界面处理，有利于处理多介质多物理场的耦合[23-26]。光滑粒子流体动力学（smoothed particle hydrodynamics, SPH）方法作为应用最广泛的粒子类方法，被很多研究者用于模拟航行体的入水问题[27-29]。Zhao等[30]采用SPH方法，对波浪条件下的结构物入水问题和流场细节进行了模拟分析。Yan等[31]采用更新拉格朗日粒子流体动力学方法对复杂结构物的入水问题进行了模拟，并很好地捕捉了刚体入水过程中周围形成的水冠、空腔形状和流场细节。航行体在波浪中高速入水的数值模拟，相对于静水工况，存在着波浪建模、液面剧烈变形及液滴飞溅、刚体六自由度运动响应计算等难点，而针对波浪的SPH方法建模，也往往采用推板造波的方式，并设置消波区来消除波浪反射，这增加了计算规模和复杂度，并且推板造波需要一定的时间形成稳定的波浪，不适合航行体高速瞬时入水的模拟。

因此，本文采用SPH方法，提出一种新型的周期性波浪边界技术，建立波浪条件下的数值水池，之后采用四元数法计算航行体的六自由度运动，通过SPH方法与四元数法结合，对高速航行体在不同波浪相位角下的入水过程展开数值模拟，得到不同波浪相位角下航行体入水的六自由度运动轨迹，以期为高速入水航行器的工程设计提供计算工具和理论依据。

1 数值计算方法

1.1 SPH方法基本理论

本文采用Antuono等提出的δ-SPH方法[32]，该方法易于实现，与标准弱可压光滑粒子流体动力学（weakly compressible smoothed particle hydrodynamics,WCSPH）相比，其主要优点是更具稳定性，可避免高频振荡下出现非物理能量。

δ-SPH方法的主要控制方程如下：

其中：连续性方程和动量方程右侧最后一项分别为密度耗散项和人工黏性项；D/Dt表示跟随流体微团运动的导数，称之为对时间t的物质导数或拉格朗日导数；ρ、u和r分别表示流体微团的密度、速度矢量和位置矢量；g为体积力产生的加速度(本文中指重力加速度)；p、V分别代表压力和体积；α和δ分别为密度耗散项系数和人工黏性系数，本文中皆取0.1；下标i、j表示粒子编号；W为核函数；h为光滑长度；c0、ρ0分别为流体声速和流体参考密度。

1.2 波浪数值模型

为研究波浪环境下高速航行体入水的冲击载荷和运动轨迹，本研究基于有限水深波浪理论建立波浪数值模型[33]。波面方程为：

其中：η为波浪在t时刻x位置的高度；初始化时刻t为0；H为波高；ω=2π/T为频率，T为波浪周期；k=2π/L为波数，L为波长。L可以根据色散方程得到[33]：

其中d为静水深度。速度势函数[19]的表达式如下：

其中x和y是横坐标和纵坐标。根据速度势函数和水深可以得到波浪某一位置的速度和压力[33]：

其中u和v分别是x方向和y方向的速度。根据式（5）计算的速度和压力赋予波浪粒子初始速度和压力值。

1.3 周期性波浪边界技术

造波一直是建立波浪数值水池的关键问题，如果采用传统的推板造波方法，需要在波浪演化尾部加入海绵层消波区域来降低波浪的反射，处理相对复杂，计算域也相对较大，且波浪的稳定也需要一定的时间，因此并不适合用于航行体高速入水工况的计算。本文提出一种新型周期性波浪边界技术，在处理造波问题上具有很大的优势：只需将波浪数值水池中的SPH粒子按照波浪数值模型赋予初始速度和压力，流体域长度满足波长的整数倍，采用周期性边界即可实现波浪的稳定流动，且波浪的稳定不需要时间，非常适合航行体高速入水工况的计算。因此，本文在三维波浪数值水池的边界处理中，对波浪的入口和出口区域采用了周期性边界技术，如图1所示。

当流体粒子流出计算域并进入右侧的出口区域时，粒子携带着所有的物理信息，立刻转移到流体区域的最左侧，作为计算域的流入粒子。出口区域和入口区域的虚粒子由流体域两侧的粒子复制生成，作为计算域的边界条件。采用周期性边界后，可以模拟波浪的稳定流动，出口边界和入口边界的流量可以保持守恒。采用周期性边界的波浪数值水池模拟结果如图2所示，可以看出施加周期性边界之后，经过一段时间的运动，波形和波浪压力分布依然保持稳定。

图2 波浪的压力分布Fig. 2 Pressure distribution of waves

为了研究计算域大小对于施加周期性边界的数值水池的影响，本文对不同计算域的波浪水池进行了模拟。标准波浪水池长度为2L= 3.12 m，宽度为D= 0.6 m，然后建立4L×D和2L× 2D的波浪水池，得到不同计算域下波浪水池的速度场模拟结果，如图3所示。从图3中可以看出，不同计算域波浪水池的速度场在同一时刻保持一致，证明了计算域的大小对于波浪水池的影响很小。同时速度场也与线性波的理论速度场保持一致，证明了采用周期性边界的波浪数值水池的有效性。为了提高计算效率，本研究中的波浪数值水池主要采取2L×D的计算域。

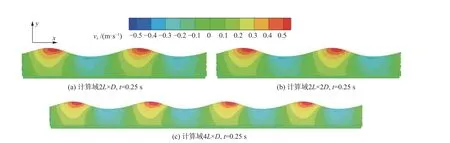
图3 不同计算域下波浪的速度分布Fig. 3 Velocity of waves in different computational domains

1.4 四元数方法

流体-刚体耦合运动问题中，涉及到两种坐标系，分别为以大地为基准的惯性坐标系（也称固地坐标系）和以运动刚体为基准的非惯性坐标系（也称随体坐标系）。随体坐标系的坐标原点Ob位于物体质心处，如图4所示。本文中流体流动和刚体的平动在固地坐标系中计算，但是刚体的转动角速度和角加速度在随体坐标系中进行计算。

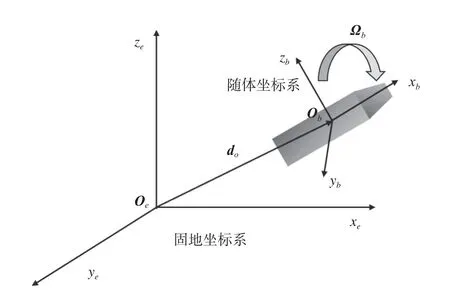
图4 坐标系转化示意图Fig. 4 Schematic of coordinate system transformation

航行体在波浪中的运动轨迹非常复杂，涉及到六自由度的运动响应。传统的六自由度运动计算往往是基于欧拉角法，但欧拉角法在计算随体坐标系和固地坐标系之间角速度的转化时，角速度变换矩阵中存在着奇异值，这会导致欧拉角法在计算刚体翻转过程中出现误差。四元数法相对于传统的欧拉角法，其角速度和四元数之间的变换矩阵中不存在奇异值，可以适应不同姿态下刚体六自由度运动的计算，在刚体翻转情况下的计算精度更高[34]。因此，本研究中采用四元数法来计算刚体的六自由度运动。

在数值水池中，刚体在固地坐标系中的物体合力Fe和力矩Te可根据下列公式[12]得到：

其中，do为连体坐标系中物体的质心坐标。初始四元数[q0q1q2q3]T是由初始欧拉角Θe=[αβγ]T得到[17]，转换关系如下：

四元数构建坐标系转换矩阵R表达式为[17]：

随体坐标系下的力矩Tb和合力Fb可通过转换矩阵R得到[35]，具体公式如下：

质心加速度和转动角加速度公式[35]如下：

式中：M为物体质量，Ib为相对质心Ob的转动惯量矩阵。通过时间步积分可以得到随体坐标系下的质心速度Ub和转动角速度Ωb，以及每个粒子在随体坐标系下的速度vb, j和加速度ab, j[35]：

固地坐标系下的质心速度Ue和转动角速度Ωe的计算[35]可根据以下公式：

Q为随体坐标系下角速度和固地坐标系下四元数变化率之间的转换矩阵[17]，表达式为：

从公式（13）中可以看出，随体坐标系中角速度到固地坐标系四元数变化率的转化矩阵中不存在奇异值，适合任何姿态的计算。在得到四元数变化率后，通过时间步积分可以更新四元数，进而更新转换矩阵R。固地坐标系下的粒子位置和速度信息也可以实时更新[35]，具体公式如下：

四元数的完整计算流程如图5所示。

图5 四元数法流程Fig. 5 Flow chart of the Quaternion method

1.5 六自由度运动计算验证

为了验证基于四元数法的六自由度运动计算精度，本文同时采用自主编制的SPH程序和基于有限体积法（finite volume method, FVM）的成熟商业软件STAR-CCM+，对方块体六自由度落水过程进行模拟，通过SPH与FVM结果对比，验证方块体六自由度运动的数值计算精度。

方块体落水示意图如图6所示。方块体长度为128 mm、宽度为68 mm、厚度为4 mm，质量为0.2184 kg，质心距方块体底部65.2 mm、距离水面67.2 mm，方块体连续绕y轴和z轴旋转25°，转动惯量Ix、Iy、Iz分别为0.00039676 、0.00009、0.0003082 kg·m2。

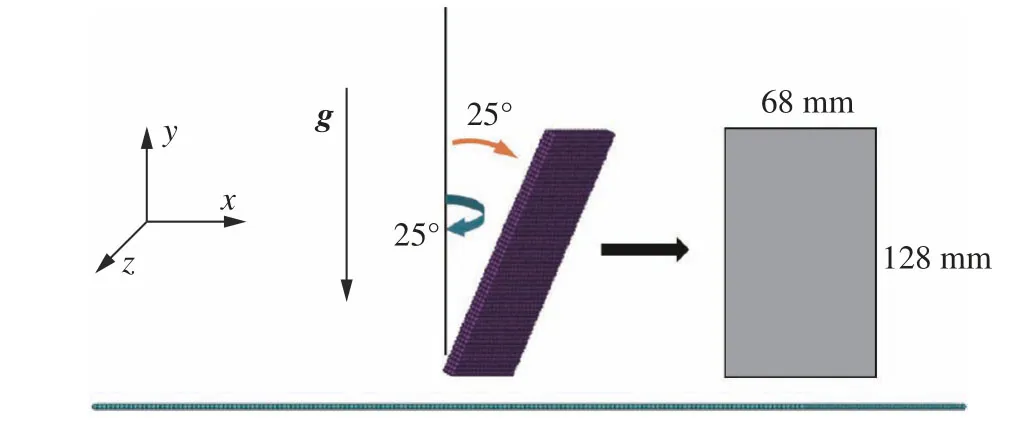
图6 方块体落水示意图Fig. 6 Schematic of a cuboid falling into water

图7为采用SPH和FVM方法对方块体落水过程的模拟结果，方块体落水的速度变化曲线如图8所示。可以看到，基于四元数法的SPH方法模拟结果与FVM的模拟结果吻合得很好。

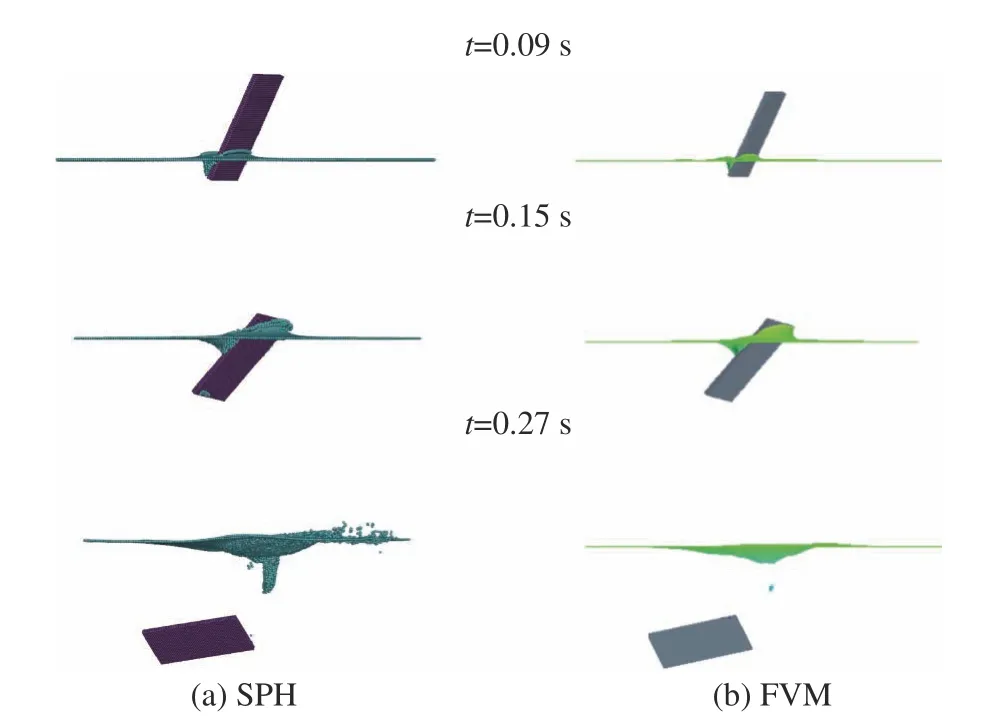
图7 方块体落水的SPH和FVM模拟结果Fig. 7 SPH and FVM simulation results of a cuboid falling into water

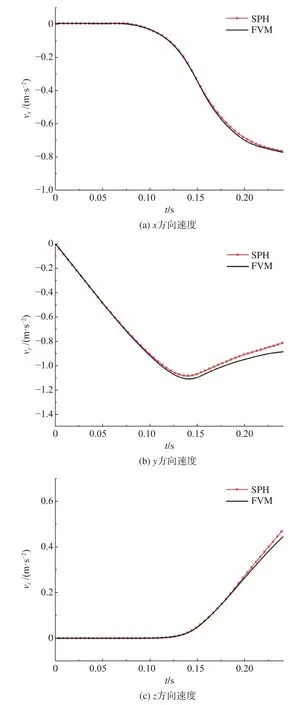
图8 方块体落水的的速度曲线Fig. 8 Velocity curve of a cuboid falling into water

2 航行体数值模型建立与验证

为了更好地与文献结果进行对比验证，本文以杨晓光等开展的高速航行体斜入水研究[19]为参考，选用相同的工况条件进行计算。航行体质量为1.35 kg，质心距前端面为123 mm，转动惯量Ix、Iy、Iz分别为0.00059、0.005186、0.005186 kg·m2。航行体几何示意图如图9所示。平静水面下的航行体入水数值模型见图10。为了降低计算规模，提高计算效率，同时保证刚体周围流场的模拟更为精细，本文使用了多分辨率技术[36]，加密区域粒子随刚体的运动动态加密，如图10（b）所示。

图9 航行体几何示意图Fig. 9 Geometric diagram of the projectile

在进行数值模拟之前，首先进行粒子间距的收敛性分析。选择粒子间距分别为10.0、5.0、2.5 mm，计算得到3种不同粒子间距下y方向航行体的加速度ay变化曲线，见图11。当粒子间距小于5 mm时，计算结果趋近于收敛。因此，为了提高计算效率，在后续算例中采用5 mm的粒子间距。

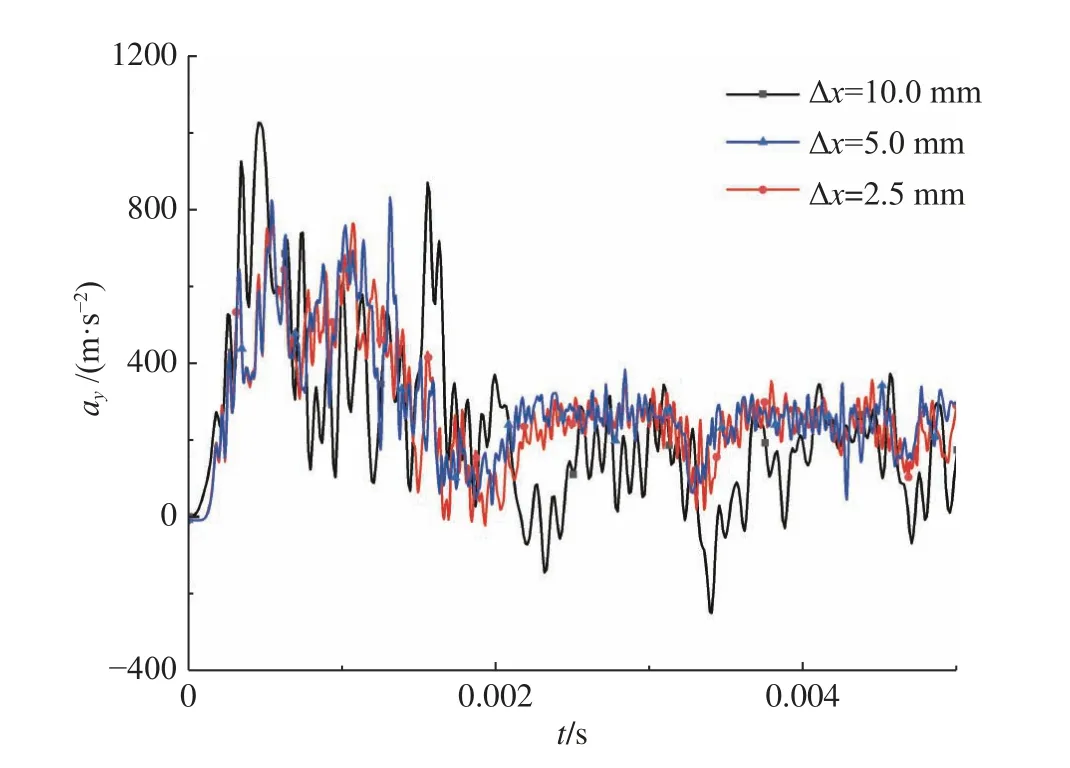
图11 不同粒子间距下的y方向航行体加速度Fig. 11 The y-direction accelerations of the projectile with different particle sizes

随后，通过在静水状态下的航行体高速入水模拟来验证本文SPH方法的可行性。文献[19]的航行体高速入水试验在静水状态下开展，航行体入水速度为60 m/s，入水倾角为20°。本文针对相同工况开展了数值模拟研究，从轴向加速度aA对比结果图12可见，SPH方法的模拟结果与试验结果吻合得很好，验证了本文SPH模型对航行体入水冲击载荷的预报精度。

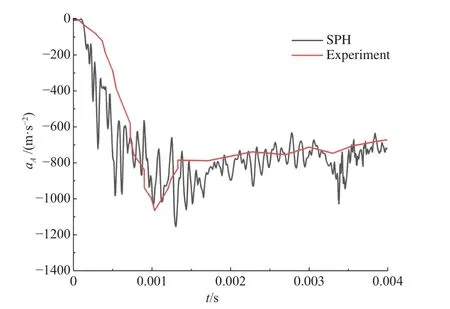
图12 SPH方法航行体轴向加速度和试验结果[19]的对比Fig. 12 Comparison of the axial acceleration of the projectile between SPH simulation results and experimental results[19]

同时，在文献[19]中杨晓光等也采用了网格类CFD方法对静水工况下的航行体入水进行了模拟。本文针对相同工况，开展了无网格数值模拟研究。SPH方法与网格法在不同时刻的模拟结果对比如图13所示，可以看出，SPH方法预报的弹体运动和自由面变形情况均与文献结果吻合良好。此外，SPH结果中捕捉到了更为显著的液滴飞溅，凸显了无网格算法捕捉自由液面大变形的优势。

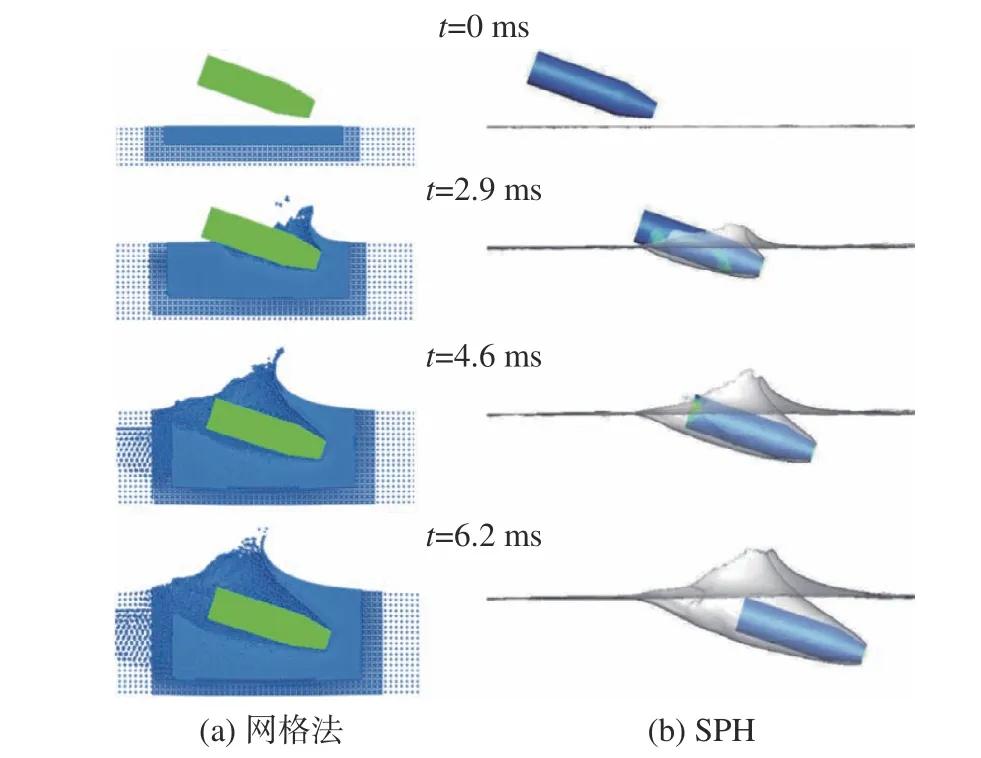
图13 SPH方法航行体入水模拟结果和文献结果[19]的对比Fig. 13 Comparison of water-entry simulation results of the projectile between SPH method and Ref.[19]

3 波浪环境下的航行体入水模拟

在波浪环境下航行体入水的SPH模拟中，波浪参数设置与杨晓光等[19]的数值模型一致。波浪周期T为1 s，波高H为0.15 m。在0.6 m的水深下，波长L为1.56 m。数值水池计算域长度为3.12 m，为两倍波长，宽度D为0.6 m。

航行体以与水平面20° 的倾角、60 m/s的速度入水，选择4个波浪相位点入水展开数值模拟，分别为0°、90°、180°和270°，入水点如图14所示。航行体的质心与对应相位点的连线与水平面成20° 的倾角。

图14 航行体入水位置的波浪相位角Fig. 14 Wave phase angles at the entry position of the projectile

3.1 不同相位角的模拟结果

航行体在波浪90° 和270° 相位角入水的模拟结果如图15所示。

图15 航行体入水过程的SPH模拟结果Fig. 15 SPH simulation results of the projectile in the waterentry process

从图15中可以看出，航行体在入水后姿态角发生偏转，头部上扬，在90° 的相位角入水工况中，入水15 ms后航行体开始冲出水面。图16给出了与杨晓光等[19]采用网格类方法结果的对比，可以看出本研究的SPH模拟结果与网格类方法的模拟结果非常吻合。其中，航行体在0° 相位角入水的模拟结果与静水状态下入水结果类似；而航行体在180° 相位角入水过程中，发生翻转，头部上扬，航行体冲出水面。两个相位角下航行体入水的SPH模拟结果与网格法模拟的航行体运动轨迹非常吻合。除此之外，得益于SPH粒子法的无网格和拉格朗日特性，可以自动构建自由液面，因此本研究能够精确高效捕捉航行体入水时飞溅液滴的形态和轨迹，如图15和图16所示。而网格类CFD方法在处理液面大变形和液滴飞溅时，需要采用Level Set或者流体体积（volume of fluid,VOF）技术进行自由液面追踪，且追踪精度受网格分辨率影响极大。图16右侧展示的网格法计算结果中，受网格尺寸限制，未能精确捕捉到液滴飞溅形态。

图16 航行体入水过程的SPH模拟结果与参考结果[19]对比Fig. 16 The comparison between SPH simulation results and Ref.[19] of the projectile in the water-entry process

3.2 不同相位角对于航行体运动轨迹的影响

为了定量分析不同相位角下航行体的入水状态和轨迹，提取了不同相位角下航行体入水后的转动角度和运动速度数据，变化曲线如图17所示。

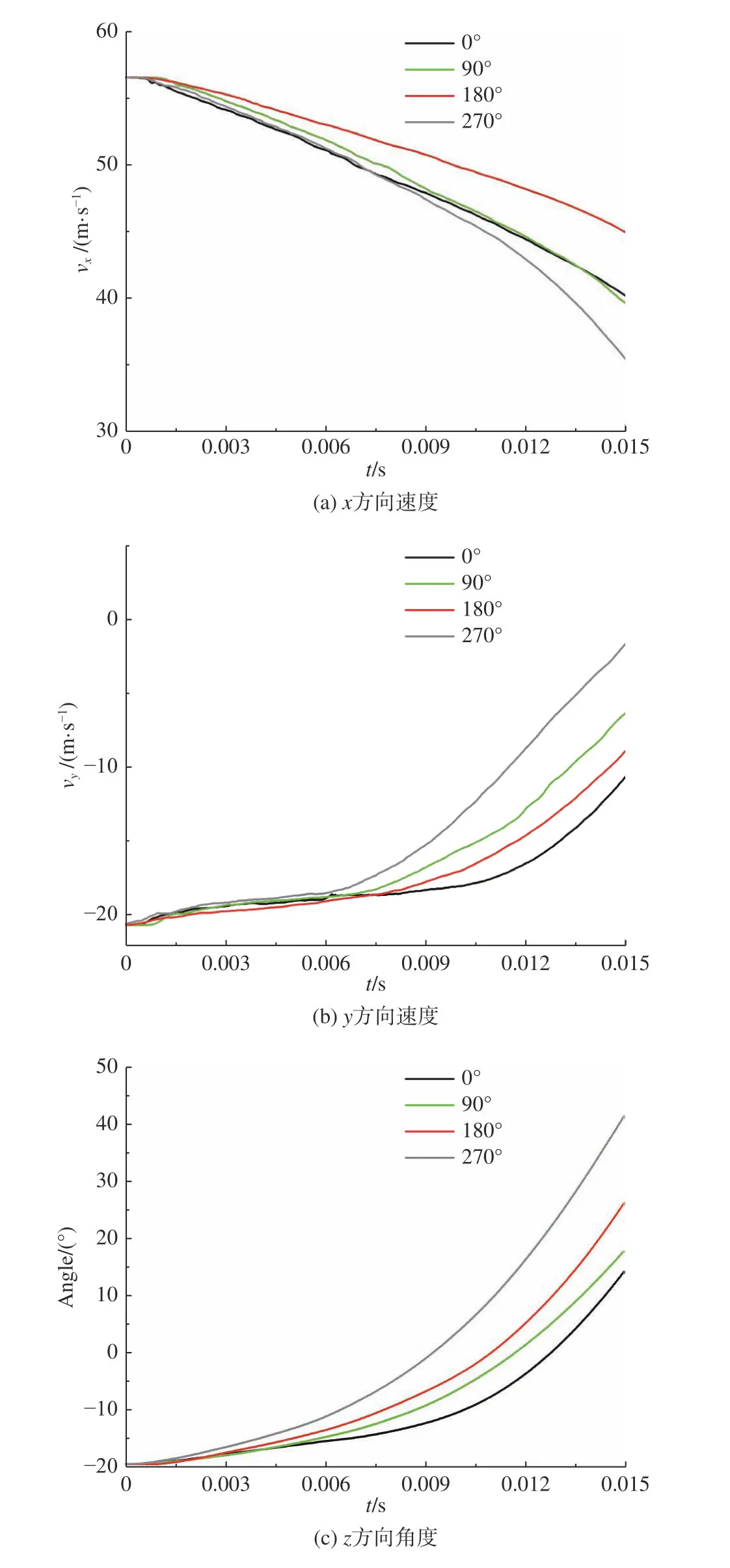
图17 不同相位角下航行体入水速度和角度变化Fig. 17 The velocity and angle curves of the projectile with different phase angles

从图17可知：4个相位角下、入水15 ms时，航行体倾斜角度全都从-20°变为正值，都呈现出头部上扬的姿态；在270° 相位角下，航行体在入水后的翻转速度最快，而在0° 相位角下航行体翻转速度最慢，所以270° 相位角下航行体的x和y方向速度衰减最快，0° 相位角下航行体y方向速度衰减最慢；而在180°相位角下，航行体入水后半浮于水面上，所以在x方向上速度衰减最慢。

由于本研究中航行体入水的速度较大，波浪流动速度的影响相对较小，相对于静水条件下的航行体入水，波浪对于航行体入水轨迹的影响主要体现在不同相位角入水对于航行体实际入水角度的改变以及波浪形状对于航行体出水时刻的影响。本文模拟的4种相位角入水工况中，根据图15和图16的模拟结果可知，0° 相位角下的航行体与水面的夹角最大，水动力载荷主要集中在轴向，侧向载荷相对较小，因此转动速度最慢，在y方向上的速度衰减最慢，弹道稳定性方面表现最好；而180° 相位角下的航行体与水面的角度很小，航行体几乎是悬浮在水面上，侧向载荷较大，因此转动角度较快，航行体也迅速出水，由于航行体半浮于水面，受到的水阻力较小，所以在x方向上的衰减更慢；而在270° 相位角下，航行体的入水角度与波面几乎平行，所以侧向载荷较大，转动速度最快，但入水后航行体进入到另一个波浪的波峰区域中，距离波面较远，出水时刻更为滞后，同时入水后的迅速转动也导致水阻力增大，所以在x和y方向的速度衰减最为明显。静水条件下的航行体入水轨迹发展主要受入水角度影响，而波浪条件下航行体入水轨迹受入水角度、波浪相位角和波浪形状的多重影响，更为复杂。