相位角对容性耦合电非对称放电特性的影响∗

胡艳婷 张钰如 宋远红 王友年

(大连理工大学物理学院,三束材料改性教育部重点实验室,大连 116024)

(2018年7月22日收到;2018年9月28日收到修改稿)

1 引 言

容性耦合等离子体(capacitively coupled plasmas,CCP)源在工业生产中有着非常广泛的应用,例如芯片制造、太阳能电池薄膜沉积以及材料表面改性等[1].在实际应用中,离子通量决定着工艺生产的效率,而离子能量则直接影响材料表面处理效果,因此对电极表面的离子能量和离子通量进行独立控制显得格外重要.在传统的单频放电中,仅调节电压和频率,无法对离子能量和离子通量进行独立控制,因此双频放电应运而生.其中,两个不同频率的电源施加在相同或不同的电极上,低频电压要远远高于高频电压.在双频容性耦合放电中,离子通量主要被高频源控制,而离子能量则主要受低频源的影响.但是,随后的一些研究表明高低频电源之间存在很强的耦合作用,且由于二次电子的原因[2−8],这种独立控制在一定范围内受到了限制.

2008年,Heil等[9]提出了一种新的技术,即电非对称效应(electrical asymmetry effect,EAE),其中基频波和其二倍频施加在同一电极上.通过调节两个频率间的相位角,即使在几何对称的腔室结构中,也可以改变直流自偏压.由于轰击到基片表面的离子能量直接受到直流自偏压的影响,因此利用EAE可以实现对离子能量和离子通量的独立调控[10−13].随着相位角从0增加为π/2,驱动电压波形从对称变成反对称,同时自偏压从最负值变为最正值.采用这种方式,可以在很大程度上避免不同频率间的耦合效应和二次电子的影响.此外,当上下极板不对称时,几何非对称所产生的自偏压会被电非对称效应所补偿[14].

2009年,Schulze等[15]对电非对称效应进行了优化,他们发现在双频放电中,当二倍频和基频的电压幅值比约为0.5时,直流自偏压的幅值最大,即能够对离子能量进行较大范围的调控.随后,为了更进一步地增大离子能量的调控范围,Schulze等[16]研究了多次谐波叠加驱动放电中的电非对称效应.研究发现,当采用优化后的电压波形(如(1)式所示)驱动放电时,与双频放电相比,直流自偏压明显增强,自偏压的幅值随着谐波阶数k的增加而增大.但当谐波阶数k大于10时,归一化的自偏压不再增大,达到一个饱和值.Lafleur等[17]也做过类似的研究,得到了与之相似的结论.2012年,Zhang等[18−20]采用PIC/MCC(particlein-cell and Monte-Carlo collision)模型,模拟研究了电负性等离子体中几何非对称效应和电非对称效应对等离子体特性的影响.研究结果表明电非对称效应仅依赖于谐波间相位角的变化,即电非对称效应和几何非对称效应互不影响.

其中k是谐波阶数,f是基频频率,θn是第n次谐波的相位角,φ(k)n是第n次谐波的电压幅值,由(2)式计算得到.

在电非对称放电中,谐波之间的相位差不仅会影响极板表面的自偏压,同时还对等离子体的径向分布产生影响.Zhang等[20]的研究发现,通过改变基频和二倍频之间的相位角θ,等离子体的径向均匀性可以得到调节:当θ=π/4时,等离子体密度在径向中心和边缘处各存在一个极值;当θ增大到3π/4时,等离子体密度仅在径向边缘处达到最大.2015年,Zhang等[21]利用HPEM(hybrid plasma equipment model)模型,研究了三频(15/30/60 MHz)容性耦合等离子体放电过程.研究结果表明:通过改变基频与倍频间的相位角,可以对等离子体的径向均匀性进行改善,且三倍频的加入会提高等离子体的密度.Schungel等[22]通过实验研究证明,在大面积容性耦合氢电非对称放电中,可以通过改变相位角来抑制由电磁效应所引起的径向不均匀.2018年,Zhang等[23]利用二维流体力学模型研究了多次谐波叠加驱动放电中的电非对称效应,研究结果显示:当考虑电磁效应的影响时,随着基频相位角从0增加到π,等离子体的空间分布从边缘最高逐渐变得均匀;而当基频相位角为3π/2时,密度的最大值又出现在径向边缘处,等离子体的径向均匀性变差.

迄今为止,尽管人们对多次谐波叠加驱动放电中的电非对称效应开展了一定的研究,但仍然存在一些问题.例如,当改变高次谐波的相位角时,自偏压以及等离子体均匀性的变化趋势仍不是很清楚.因此,本文采用二维流体力学模型,并耦合麦克斯韦方程组,系统地研究在不同的谐波阶数下,不同倍频的相位角对等离子体特性的影响并分析其原因.相关研究成果有望为优化大面积薄膜沉积或刻蚀工艺提供一定的理论依据.

2 流体力学模型

本文所采用的二维流体力学模型是由本课题组自主研发的用于描述等离子体放电过程的模拟软件——MAPS(Multi-physics Analysis for Plasma Sources)-CCP.由于MAPS-CCP在文献[24,25]中已做了详细介绍,在此只进行简要描述.

等离子体的一些宏观物理量,如粒子数密度、平均速度以及能量密度等,由玻尔兹曼的各阶矩方程给出.由于电子质量较低,电子通量采用漂移扩散近似来描述.此外,由于电子温度远远大于离子和中性粒子的温度(Te≫Ti),等离子体被当作“冷流体”.在该模型中,认为离子以及中性粒子的温度与室温相等,即仅求解电子的能量守恒方程.

模拟的反应腔室为柱状对称结构,即各物理量关于角向是对称的,因此可以将三维的腔室结构简化为二维,如图1所示.在模拟中,腔室半径Rreactor为20 cm,极板半径Relectrode为15 cm,极板间隙L为3 cm.上极板和侧壁接地,下极板接电压源,用于产生电非对称放电(由于接地电极的面积大于功率电极,因此会引起几何不对称效应,下文将会详述).驱动电压波形为文献[16]中所采用的优化后的电压波形((1)式).通过调节(1)式中的相位角θn,下极板表面的直流自偏压Vdc会发生变化.在模型中,通过迭代的方式调节Vdc,使得一个基频周期内流向两个电极的电流相等.

图1 模拟腔室结构示意图Fig.1.Schematic picture of the reactor configuration.

在本文的工作中,基频频率f=13.56 MHz,电压幅值V0=100 V,谐波阶数k在2和8之间变化.当k=2时,是双频放电;当k=3时,是三频放电;以此类推.当k=8时,最高次谐波的频率可达到108.48 MHz,即处在甚高频的范围.由于电磁波的波长与频率成反比,当放电频率增大使得电磁波的波长与腔室的径向尺寸相当时,电磁效应(即驻波效应和趋肤效应)变得明显,并会影响等离子体的径向均匀性.因此,需要求解麦克斯韦方程组,即建立电磁模型,才能精确地描述放电过程.在电磁模型中,电场E由两部分构成,即E=ES+ET(ES为静电场,ET为电磁场).在求解过程中,引入静电势ϕ和磁矢势A,静电场为ES=−∇ϕ,电磁场为ET= −∂A/∂t.进一步,引入库仑规范∇·A=0,最终麦克斯韦方程组可简化为

其中ne是电子密度,n±是正、负离子密度,Z±为正、负离子所带的电荷数,ε0是真空中的介电常数,µ0是真空中的磁导率,J为电流密度.

本文模拟采用的工作气体是H2,放电气压为200 mTorr.在该气压条件下,欧姆加热占主导,因此流体力学模型可以很好地描述等离子体放电过程.在模型中考虑了以下粒子:电子(e),正离子(H+,,)及基态原子(H).模型中考虑的化学反应如表1所列,包括电子与H原子和H2分子的碰撞电离反应,电子和离子的复合反应,H2分子的分解反应以及重粒子间的碰撞反应.其中,电子的碰撞电离反应以及H2分子的分解反应,其速率系数根据相应的碰撞截面进行估算;电子和离子的复合反应以及重粒子间的碰撞反应,其速率系数直接取自相应的文献.

表1 等离子体化学反应模型Table 1.The reactions for the plasma included in the model.

3 结果与讨论

图2给出了不同谐波阶数(k=2,3,4,8)下直流自偏压Vdc随相位角θn的变化趋势(其中,θn(n=1,2,···,8)泛指第n次谐波的相位角;当θn单独变化时,其余相位角为0).

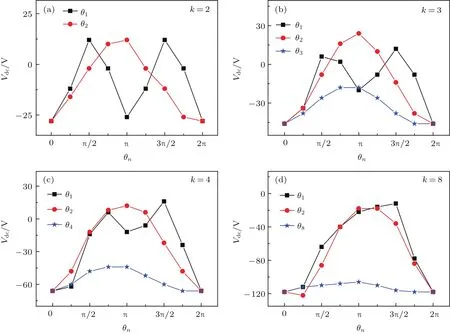
图2 不同谐波阶数k下自偏压Vdc随相位角θn的变化趋势 (a)k=2;(b)k=3;(c)k=4;(d)k=8Fig.2.Evolution of the dc self-bias with θnfor various numbers of harmonics k:(a)k=2;(b)k=3;(c)k=4;(d)k=8.

从图2中可以看到,当谐波阶数k=2时,直流自偏压Vdc的幅值在θ1=0和θ1= π/2处不相等.这是因为我们模拟的腔室结构是几何不对称的,即几何不对称效应引起的自偏压与电非对称效应相叠加,使得自偏压整体负向偏移.直流自偏压Vdc随相位角θ1和θ2的变化幅度相差无几,但变化周期从π变为2π.当k=3,4,8时,相位角θ1对自偏压Vdc的影响,与k=2时不一样:k=3时,虽然自偏压Vdc在θ1=π/2和θ1=3π/2处分别出现一个正向极值,但二者并不相等;k=4时,自偏压Vdc的第一个正向极值出现在θ1=3π/4处,且幅值要显著低于3π/2处的值;k=8时,可以明显看出,自偏压Vdc随相位角θ1的变化周期为2π.

此外,从图2还可知,谐波阶数k从2增大到8的过程中,自偏压Vdc随相位角θ2和θk的变化周期均为2π,且正向峰值大约出现在θn=π处.此外,随着谐波阶数k的增加,自偏压Vdc随最高倍频相位角θk的变化幅度逐渐减小,尤其是在k=8时,自偏压Vdc随相位角θ8仅在±5%的范围内变化.

上述现象可以根据自偏压的推算公式((4)式)来解释.从(4)式中可以看出自偏压直接受到电压波形的最大值ϕm1、最小值ϕm2以及对称参数ε的影响[9].

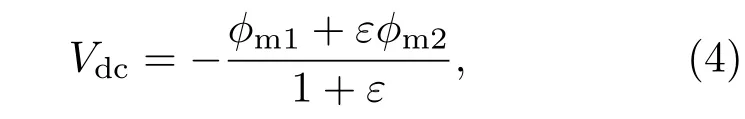
图3 不同谐波阶数k下,归一化的电压波形随相位角θn的变化趋势Fig.3.Evolution of normalized voltage waveforms with θnfor various numbers of harmonics k.

由于在不同谐波阶数k、不同相位角θn的情况下,电压波形的最大值ϕm1、最小值ϕm2以及对称参数ε不尽相同,导致图2中自偏压的变化趋势有所不同.图3给出了谐波阶数k=3,8时,不同相位角θn下采用V0归一化的电压波形(θn单独变化时,其余相位角为0).需要注意的是,根据公式当谐波阶数k=8时,而当k=3时,因此图3的两列图中纵坐标有所不同.

首先,对比图3(a),3(c),3(e)可知,当谐波阶数k=3时,电压波形的最大值ϕm1和最小值ϕm2均随相位角θn改变,且变化趋势不尽相同.譬如,当相位角θ1=π 时,|ϕm1|≈ |ϕm2|,且通过计算得知对称参数ε≈1,所以根据(4)式可知自偏压的幅值应趋近于0.但图2(b)中Vdc约为−20V,这仍是由于几何非对称效应,使得Vdc负向偏移.当相位角θ2= π时,|ϕm2|的值远大于|ϕm1|,所以Vdc为正(见图2(b)). 而当相位角θ3= π 时,|ϕm1|≈ |ϕm2|,Vdc的值和θ1=π时相等.当改变相位角θ3时,|ϕm1|−|ϕm2|的变化幅度较小,因此该条件下自偏压的变化幅度也较小(见图2(b)).此外,由于电压波形随相位角θn的变化周期为2π,且|ϕm1|−|ϕm2|的值关于θn=π对称,所以自偏压Vdc的变化周期也为2π,且变化趋势基本上关于θn=π对称.

当谐波阶数k=8,相位角θn=0时,电压波形中|ϕm1|− |ϕm2|的值大于k=3时的结果,所以自偏压Vdc的幅值也相应地增大(见图2(b)和图2(d)).对比图3(b)、图3(d)、图3(f)还可知,电压波形的最大值和最小值随相位角θn的变化趋势基本一致,变化周期都为2π.在所研究的相位角θ1,θ2,θ8的范围内,|ϕm2|的值都小于|ϕm1|, 且|ϕm1|− |ϕm2|的值关于θn= π 对称. 但由于ε的值并不关于θn=π对称,根据自偏压的计算公式((4)式),图2(d)中Vdc随相位角的变化趋势也是非对称的.除此之外,在相位角θ1,θ2从0增大到2π的过程中,|ϕm1|−|ϕm2|呈现出先减小、后增大的趋势,在π时达到最小值.通过计算可知,对称参数ε的变化比较微弱,因此图2(b)中自偏压的幅值也随着相位角先减小后增大.然而,当改变相位角θ8时,我们发现|ϕm1|− |ϕm2|的值变化甚微,所以在该条件下,自偏压仅在±5%范围内变化(见图2(d)).

在电非对称放电中,改变相位角不仅可以调节自偏压,还会对等离子体的径向均匀性产生影响[20−23].但到目前为止,大多数研究者只给出了基频相位角的影响,对于不同倍频相位角下的等离子体分布并没有进行细致的研究.所以接下来我们重点观察不同谐波阶数下不同倍频的相位角对等离子体径向均匀性的影响.

为了进一步定量分析,首先定义一个用于描述等离子体径向均匀性的物理量,即等离子体不均匀度α:

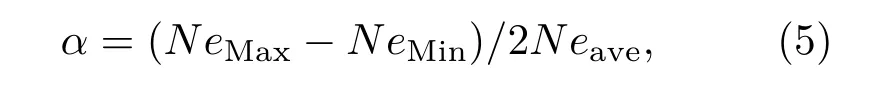
其中NeMax,NeMin,Neave分别为Z=L/2(Z对应纵坐标)处,R=0—15 cm(R对应横坐标)区间内的电子密度的最大值、最小值及平均值.

图4给出了谐波阶数k=2时,不均匀度α随相位角θn的变化趋势(θ1,θ2单独变化时,其余相位角为0).从图4中可以看出,α随相位角θ1和相位角θ2的变化范围相似,α的值大约为1%—7.6%.但α随相位角θ1的变化周期为π,α的最小值出现在θ1=π/2处;而α随相位角θ2的变化周期为2π,其最小值出现在θ2=π处.这一结果表明:当谐波阶数k=2时,基频相位角θ1和二倍频相位角θ2都可以有效地调节等离子体的径向分布,且调节强度相当.

图4 当谐波阶数k=2时,等离子体不均匀度α随相位角θn的变化趋势Fig.4.Evolution of the plasma nonuniformity degree α with θnin discharges sustained by the fundamental frequency and the second harmonic.

图5和图6分别给出了当谐波阶数k=2时,电子密度的空间分布随相位角θ1和θ2的变化趋势.

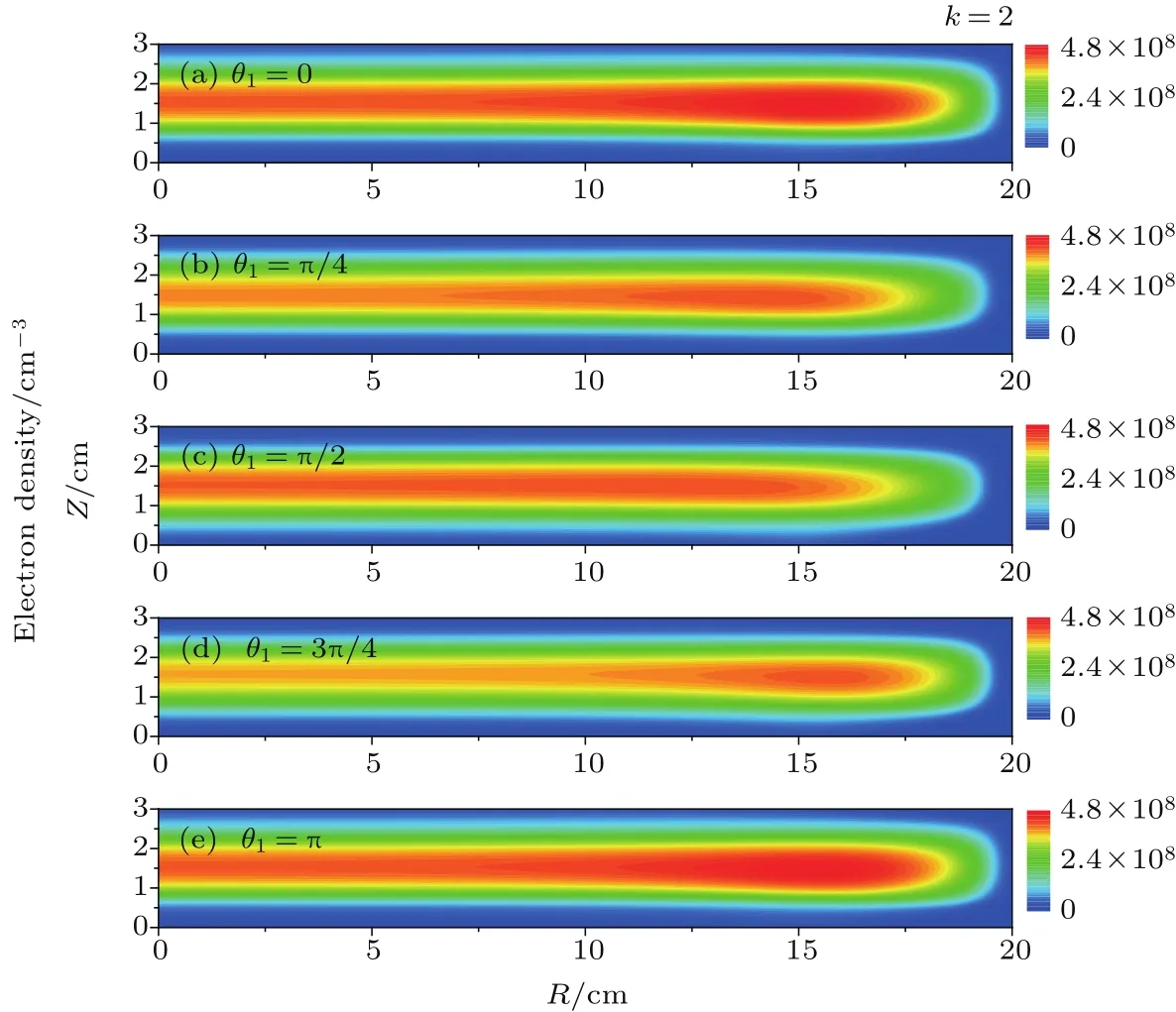
图5 当谐波阶数k=2时电子密度的空间分布随相位角θ1的变化Fig.5.Distributions of the electron density for various θ1in discharges sustained by the fundamental frequency and the second harmonic.

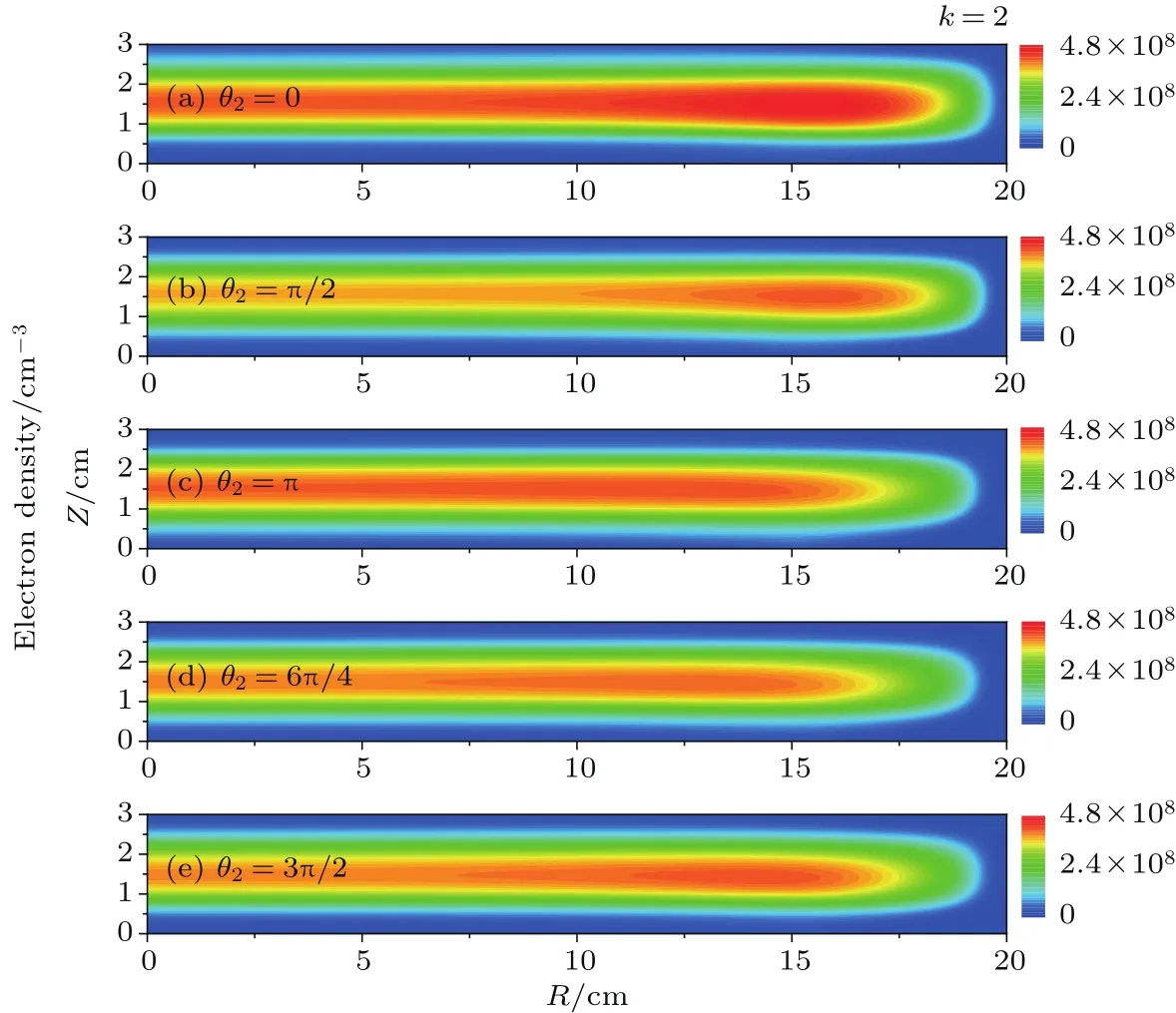
图6 当谐波阶数k=2时电子密度的空间分布随相位角θ2的变化Fig.6.Distributions of the electron density for various θ2in discharges sustained by the fundamental frequency and the second harmonic.

如图5所示,固定相位角θ2=0不变,当相位角θ1=0时(图5(a)),电子密度在径向边缘位置出现一个最大值,且体区更加靠近上电极(接地电极).这是由于下电极上的自偏压为负(见图2(a)),下电极附近的鞘层厚度大于上电极附近的鞘层厚度.当θ1增大到π/4时,径向边缘处的电子密度显著降低,但仍高于放电中心处,此时不均匀度α从6.1%下降到3.4%,等离子体的径向均匀性变好.此外,由于自偏压的幅值减小,图5(b)中主体区也逐渐向下电极移动.当θ1=π/2时,径向边缘处的电子密度略微降低,同时放电中心处的电子密度缓慢增加,因此图5(c)中等离子体的径向分布最均匀,此时不均匀度α≈1.2%(见图4).此外,由于电非对称效应产生的自偏压为正,所以下电极附近的鞘层厚度小于上电极附近的鞘层厚度.当θ1继续增大时,等离子体密度的最大值又出现在径向边缘处,等离子体的径向均匀性再次变差.如θ1=3π/4时,不均匀度α ≈5.4%;θ1= π时,不均匀度α≈6.1%.

固定相位角θ1=0,当谐波阶数k=2时,电子密度的空间分布随相位角θ2的变化趋势,如图6所示.在相位角θ2从0增加到π的过程中,径向边缘处的电子密度先下降,然后几乎保持不变,而放电中心处的电子密度先下降,后上升.因此当θ2=π时(图6(c)),等离子体的径向均匀性最好,不均匀度α仅为1.2%.此外,由于自偏压逐渐向正向移动(见图2(a)),下极板附近的鞘层逐渐变薄.然而,当相位角θ2继续增大时,电子密度的最大值再次出现在径向边缘处,如图6(e)所示.此时等离子体的径向均匀性变差,当θ2=3π/2时,不均匀度α≈3.4%.需要注意的是,图5和图6中,放电条件基本一致,仅驱动电压波形中不同谐波的相位角有所改变.由于周期平均的电子吸收功率并不随相位角改变,因此等离子体密度的幅值几乎固定不变[30].

以上结果说明,当谐波阶数k=2时,相位角θ1,θ2对电子密度空间分布的影响是不同的.当固定相位角θ2=0时,等离子体的径向均匀性在θ1= π/2时最好;当固定相位角θ1=0时,等离子体的径向均匀性在θ2=π时最好.同理,当放电由多次连续谐波叠加驱动时,也可以利用不同倍频的相位角对等离子体的径向分布进行调节.

图7给出了当谐波阶数k=3时,腔室轴向中心(Z=L/2)处电子密度的径向分布以及等离子体不均匀度α随相位角θn的变化趋势(θ1,θ2,θ3单独变化时,其余相位角为0).从图7(a)可知,当相位角θ1=0时,电子密度在径向边缘位置出现一个最大值.当θ1增大到π/2时,径向边缘处的电子密度显著降低,而放电中心处的电子密度基本保持不变,因此等离子体的径向分布变得均匀,不均匀度α从7.8%减小到2.48%(见图7(d)).随着θ1进一步增加,放电中心处的电子密度继续降低,当θ1=3π/2时,径向均匀性最优,不均匀度α仅为0.41%.然而,当θ1增大到7π/4时,电子密度再次呈现出边缘高的分布,不均匀度α≈9.27%,等离子体的径向均匀性变差.

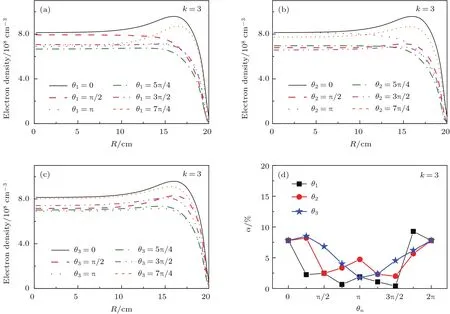
图7 当谐波阶数k=3时轴向中心(Z=L/2)处电子密度的径向分布以及等离子体不均匀度α随相位角θn的变化趋势Fig.7.Radial distributions of the electron density along the reactor centerline(Z=L/2)and the plasma nonuniformity degree α for various θnin discharges sustained by three consecutive harmonics.

类似地,从图7(b)中可以观察到,随着相位角θ2增加为π/2,径向边缘处电子密度的下降速度快于放电中心处,因此等离子体的径向分布得到改善,不均匀度α降低为2.46%(见图7(d)).当θ2=π时,径向边缘处的电子密度几乎不变,而放电中心处的电子密度迅速增大,使得等离子体的均匀性变差,不均匀度α≈4.7%.随着相位角θ2继续增大,放电中心处的电子密度再次降低,与径向边缘处的幅值相当,等离子体的径向均匀性在θ2=3π/2时达到最佳.然而,当相位角θ2=7π/4时,电子密度整体增大,且最大值再次出现在径向边缘处,使得径向均匀性又变差.固定θ1,θ2不变时,随着相位角θ3从0变化到π,径向边缘处和放电中心处的电子密度均单调下降,但径向边缘处的下降幅度较大,如图7(c)所示.因此,等离子体的径向分布逐渐变得均匀,不均匀度α从7.8%减小到1.7%(见图7(d)).当相位角θ3继续增大时,电子密度单调递增,且径向边缘处的幅值增加速率较快,使得等离子体的径向均匀性再次变差.如相位角θ3=7π/4时,α ≈ 6.2%.

图8 当谐波阶数k=4时轴向中心(Z=L/2)处电子密度的径向分布以及等离子体不均匀度α随相位角θn的变化趋势Fig.8.Radial distributions of the electron density along the reactor centerline(Z=L/2)and the plasma nonuniformity degree α for various θnin discharges sustained by four consecutive harmonics.

当谐波阶数k=4时,不同相位角θn(θ1,θ2,θ4单独变化时,其余相位角为0)对电子密度的径向分布以及等离子体不均匀度α的影响又有所不同.如图8(a)所示,当相位角θ1从0增大到π/2时,电子密度的径向分布从边缘高变为中心高,不均匀度α从10%降低为1.75%.当相位角θ1继续增大时,电子密度整体下降,最均匀的径向分布出现在θ1=5π/4时,不均匀度α仅为1.4%.然而,在相位角θ1继续增大到7π/4的过程中,径向边缘处的电子密度逐渐增大,但放电中心处的幅值几乎不变,因此径向均匀性再次变差.

相位角θ2对等离子体径向分布的影响,如图8(b)所示.当相位角θ2等于0和7π/4时,径向边缘处的电子密度显著高于放电中心处,等离子体的径向均匀性较差.在其他的相位角下,径向边缘处的电子密度显著降低.当相位角θ2=3π/2时,径向均匀性最好,不均匀度α≈1.37%.当相位角θ4改变时,等离子体密度始终呈现出边缘高的分布,如图8(c)所示.在相位角θ4从0变化到7π/4的过程中,电子密度的幅值先下降,后上升.当相位角θ4=π时,电子密度最低,但径向均匀性相对较好,不均匀度α约为5.7%(见图8(d)).与改变相位角θ1,θ2的情况相比,θ4对等离子体分布的调节作用较弱,径向均匀性整体较差.

图9给出了当谐波阶数k=8时,腔室轴向中心(Z=L/2)处电子密度的径向分布以及等离子体不均匀度α随相位角θn的变化趋势(θ1,θ2,θ8单独变化时,其余相位角为0).从图9(a)可知,随着相位角θ1从0变化到π,径向边缘处的电子密度单调下降,而放电中心处的电子密度先略微上升然后降低,因此等离子体的径向均匀性逐渐变好.当相位角θ1=π时,径向均匀性最优,不均匀度α≈1.9%.当相位角θ1继续增大时,径向边缘处的电子密度逐渐增大,且增涨幅度大于放电中心处,所以径向均匀性再次变差.与改变θ1的情况相比,相位角θ2对等离子体径向分布的影响有所减弱,如图9(b)所示,但对不均匀度α的调节作用类似.然而当固定相位角θ1,θ2不变时,电子密度的径向分布几乎不随θ8改变,仅幅值略有差异,如图9(c)所示.此外,不均匀度α随相位角θ8的变化范围显著减小,且径向均匀性整体较差.这是由于根据本文所采用的电压波形,最高次谐波的电压幅值远低于低次谐波,因此其相位角θ8对等离子体的调控作用较弱.在实验上,如果想增加高次谐波相位角的调控作用,需适当增加高次谐波的电压幅值.

图9 当谐波阶数k=8时轴向中心(Z=L/2)处电子密度的径向分布以及等离子体不均匀度α随相位角θn的变化趋势Fig.9.Radial distributions of the electron density along the reactor centerline(Z=L/2)and the plasma nonuniformity degree α for various θnin discharges sustained by eight consecutive harmonics.

综上可知,在不同的谐波阶数k下,相位角θn对电子密度径向分布的影响存在差异:低次谐波相位角的调制作用较为显著,而高次谐波相位角的影响则受到限制.这一现象可以通过功率密度随相位角θn的演变行为来解释.

图10给出了当谐波阶数k=3时,轴向中心(Z=L/2)处功率密度的径向分布随相位角θ2的变化情况.当相位角θ2=0时,从图10(a)中可以看到,轴向功率密度Pz(轴向电流密度和轴向电场的乘积)在径向边缘附近(R≈15 cm)和径向中心(R=0 cm)处各存在一个局域最大值.从图10(b)中可知,由于边缘处的电场较强,径向功率密度Pr(径向电流密度和径向电场的乘积)的最大值大约出现在R=18 cm处.通过比较Pz和Pr的幅值可知,当相位角θ2=0时,Pr和Pz的峰值相当,大约为6.5×103W/m3,因此径向边缘处的总功率密度大于放电中心处,所以电子密度呈现出边缘高的分布(见图7(b)).当相位角θ2=π/2时,径向边缘处的Pz和Pr均有所减小,且Pr的峰值更加靠近侧壁,因此该条件下等离子体的径向均匀性得到改善.然而,当相位角θ2增大到π时,放电中心处的Pz略有增加,而径向边缘处的Pr显著降低,所以电子密度呈现出中心高的分布.当相位角θ2=3π/2时,放电中心处的Pz与径向边缘处的总功率密度相当,因此等离子体的径向分布最均匀.当相位角θ2继续增大到7π/4时,径向边缘处的Pz略有增大,且Pr也显著增加,所以此时电子密度的最大值再次出现在径向边缘处.

图10 当谐波阶数k=3时轴向中心(Z=L/2)处功率密度的径向分布 (a)功率密度的轴向分量Pz,(b)功率密度的径向分量Pr随相位角θ2的变化趋势Fig.10.Radial distributions of the power density along the reactor centerline(Z=L/2)for various θ2:(a)The axial component of the power density Pz,(b)the radial component of the power density Pr,in discharges sustained by three consecutive harmonics.

图11 当谐波阶数k=8时轴向中心(Z=L/2)处功率密度的径向分布 (a)功率密度的轴向分量Pz,(b)功率密度的径向分量Pr随相位角θ8的变化趋势Fig.11.Radial distributions of the power density along the reactor centerline(Z=L/2)for various θ8:(a)The axial component of the power density Pz,(b)the radial component of the power density Pr,in discharges sustained by eight consecutive harmonics.

类似地,图11给出了当谐波阶数k=8时,轴向中心(Z=L/2)处功率密度的径向分布随相位角θ8的变化情况.由图11(a)可知,在所考察的相位角θ8的所有值下,轴向功率密度Pz的分布几乎不变,即在径向中心(R=0 cm)处存在一个最大值,并沿着径向方向逐渐减小,大约在R=15 cm处出现第二个局部最大值,最后在边缘位置迅速减小为0.而径向功率密度Pr始终呈现出边缘高的分布,且其峰值随相位角θ8先降低后增加,但其幅值总是显著高于Pz,如图11(b)所示.例如,当相位角θ8=0时,功率密度Pr的峰值约为6×104W/m3,大约是Pz的两倍.因此,电子密度的空间分布几乎不随相位角θ8改变,其最大值始终出现在径向边缘处,等离子体的径向均匀性较差,不均匀度α仅在11.5%—13.5%范围内变化.此外,由于径向电子通量的幅值沿径向方向先增大后减小再增大,而径向电场在R=20 cm附近突然增大,因此功率密度Pr在R=20 cm附近出现第二个局部峰值.但由于径向边缘处电子扩散到器壁上并损失,因此图9中电子密度并不存在二次峰值.

4 结 论

本文采用自洽的二维流体力学模型,并耦合麦克斯韦方程组,系统地研究了在由多谐波叠加驱动的容性耦合氢等离子体放电中,当考虑电磁效应时,不同谐波阶数k下的电非对称效应,重点观察了相位角θn对等离子体特性,尤其是对等离子体径向均匀性的影响.研究结果表明在双频放电中,直流自偏压Vdc随相位角θ1和θ2的变化幅度相差无几,但变化周期从π变为2π.当谐波阶数k增大时,自偏压Vdc随相位角θn的变化周期均为2π,且相位角θn对自偏压Vdc的影响是不一样的.此外,随着谐波阶数k的增大,自偏压Vdc随最高倍频相位角θk的变化幅度逐渐减小,尤其是当k=8时,自偏压Vdc随相位角θ8的变化范围仅为±5%.

通过改变相位角θn,不仅可以调节自偏压Vdc的幅值,还会对等离子体的径向分布产生影响,且不同谐波的相位角对均匀性的影响各不相同.当谐波阶数k=2时,相位角θ1= π/2和θ2= π时,等离子体的径向均匀性最佳.而当谐波阶数k=3时,基频相位角θ1=3π/2时,等离子体的不均匀度α最低,仅为0.41%.值得注意的是:当谐波阶数k=8时,通过改变相位角θ1和θ2,不均匀度α的最大值是最小值的7倍,即等离子体的径向均匀性可以被有效地调节.这是由于通过选取不同的相位角,可以改变功率密度Pr和Pz的相对关系.当放电中心处的总功率密度与边缘处的幅值相当时,等离子体的径向均匀性达到最佳.然而当谐波阶数k=8时,电子密度的空间分布几乎不随相位角θ8而改变,等离子体密度的最大值始终出现在径向边缘处.这是由于Pr在径向边缘处存在一个峰值,且大约是Pz的两倍,等离子体分布主要受到Pr的影响.

总之,本文的模拟结果揭示了不同谐波阶数k下自偏压Vdc随相位角θn的变化趋势以及电非对称效应对等离子体径向均匀性的调节作用.本文的研究结果表明在电非对称放电中,不仅可以实现对离子能量和离子通量的独立控制,还可以有效地调节等离子体的径向均匀性,可为优化大面积薄膜沉积或刻蚀工艺提供一定的理论依据.