基于粒子图像分割的混合PIV-PTV算法

李 拓，张清福，潘 翀，2，陈 爽，申俊琦，王宏伟，李晓辉，黄 湛，王晋军

(1. 北京航空航天大学 流体力学教育部重点实验室，北京 100191；2. 北京航空航天大学宁波创新研究院 先进飞行器与空天动力创新研究中心, 宁波 315800；3. 中国空气动力研究与发展中心 设备设计与测试技术研究所, 绵阳 621000；4. 中国航天空气动力技术研究院, 北京 100074)

0 引言

粒子图像测速（particle image velocimetry, PIV）和粒子追踪测速（particle tracking velocimetry，PTV）等基于数字图像处理的速度场测量技术被广泛应用于空气动力学测试领域[1]，是科研工作者探索流体运动规律的有效工具[2]。

PIV技术[3]的原理是向流动中添加示踪粒子，示踪粒子随流体一同运动，通过分析相机曝光得到的粒子图像上局部光流信息（一般由查询窗口内的一组示踪粒子提供）随时间的变化得到当地的速度信息。PTV技术通过追踪每个示踪粒子在双帧曝光图像中的位置变化实现速度场的测量。不同的测速原理使得两种方法适用于不同的场景：PIV技术要求每个查询区至少有三个及以上粒子；而PTV技术则要求测量区域中示踪粒子稀疏，易于识别和匹配。

PIV能够适用于示踪粒子浓度较高的场景，但需对查询窗口内的光流信息进行追踪或匹配，导致其空间分辨率受限；而PTV能够追踪单个粒子的跨帧位移，但难以处理示踪粒子间距小、跨帧位移大的场景。近年来，PIV和PTV技术手段迅猛发展[4-11]，极大地提高了测量性能，但众多学者仍希望能通过混合使用PIV和PTV以更进一步地提高测量性能[12-16]。Cowen[13]开发了DPTV技术， 通过使用PIV的估计值以限制在第二幅图像中粒子的搜索窗口，使得PTV可以在较高的粒子密度下进行匹配。Kim等[14]将PIV结果用于确定PTV过程中的匹配参数和结果验证，提高了粒子匹配效率。Benkovic等[15]将基于匹配概率的松弛算法集成到基于视觉的特征关联概念中, 通过仿真证明了结合PIV预分析的混合方法有助于减少错误向量的数量。此外，Zhu等[16]对风沙两相流中离散相颗粒和连续相示踪粒子进行分相处理，并分别使用PIV和PTV技术，实现了风沙两相速度场的同步测量。这些混合算法有效地拓宽了粒子图像测速能力，提高了测量的精度。

另外，在复杂流动中，示踪粒子在流场空间难以均匀分布的问题十分常见。例如，在边界层流动测量实验中，示踪粒子难以进入边界层内的高剪切区，致使示踪粒子在边界层内的分布过于稀疏，无法进行有效的互相关计算，导致PIV得到的速度场在近壁区域存在显著误差。针对这一问题，通常的解决手段是提高示踪粒子的整体浓度。然而，该方法对流动分离区、旋涡内部和激波后方流区的示踪粒子浓度改善效果有限。Brooks等[17]通过壁面粒子注射装置直接从壁面处将示踪粒子注入到边界层内的近壁流区，提高近壁区域的粒子密度。这种方法在边界层测量中取得了一定的效果，但不具有泛化能力。

针对上述问题，本文提出了一种基于粒子图像分割的混合PIV-PTV算法。该算法使用维诺多边形图像分割方法，对粒子图像按粒子分布浓度划分出粒子稀疏区和稠密区，对稀疏区和稠密区分别调用PTV和PIV算法，实现示踪粒子分布不均情况下的高精度流场测量。

1 算法介绍

1.1 算法流程

本文所发展的基于粒子图像分割的混合PIVPTV算法主要分为以下4个步骤：示踪粒子识别、应用维诺多边形计算示踪粒子密度、设定阈值并使用支持向量机（support vector machine, SVM）进行粒子图像划分、分别调用PIV和PTV计算速度场。其算法概述如图1所示，本节将对实现该算法的几个关键步骤进行介绍。

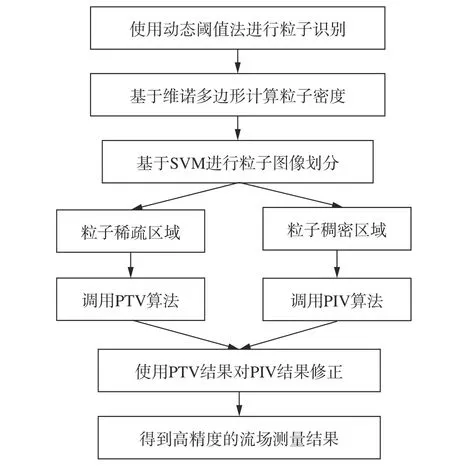
图1 混合PIV-PTV算法技术路线Fig. 1 Hybrid PIV-PTV algorithm flow chart

1.2 粒子识别

Ohmi等[18]首先提出了基于动态阈值的示踪粒子识别方法。根据粒子图像上每个粒子的平均亮度水平自适应地调整阈值，消除了传统方法基于单一或多个阈值解带来的人工确定阈值的不确定性。Mikheev等[19]对此方法进行了改进，其基本思想是将每个粒子图像的分割阈值设置为峰值的比例值，而不是原始算法中的平均值。近几年基于机器学习等方法的粒子识别技术也得到迅猛发展[20]，并展现出了优异的性能。综合考量现有方法的易用性和鲁棒性，本文选用经典的改进动态阈值法[19]，其总体方案如图2所示。

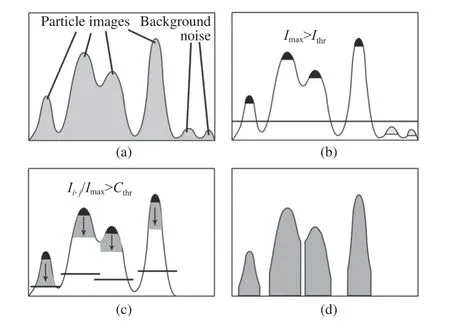
图2 改进动态阈值法实现流程[19]Fig. 2 Process of improved dynamic threshold method[19]

首先使用一定的阈值进行滤波，以排除噪声背景的干扰；寻找滤波后粒子图像的所有局部极大值，即亮度峰值点，如图2（b）。然后将每个峰值像素点扩展一个像素大小的边界，并检查每个新像素。边界像素强度与峰值像素强度之比应大于预设的对比度阈值，即：

式中：Ii,j为新添加边界像素的灰度值，Imax为峰值点的灰度值，Cthr为对比度阈值。如果满足此条件，则认为该像素与峰值像素点属于同一个粒子；否则，则认为该像素不属于该粒子。这个扩展过程持续向外进行，直到不存在满足要求的像素点。扩展过程中若遇到灰度值反常增大，则认为出现拐点，沿此方向的扩展停止。这一粒子识别算法使用了更合理的阈值准则，并能通过拐点检测在扩展过程中自动分离出重叠的粒子，具有很高的鲁棒性。

1.3 粒子浓度定义

由粒子图像测速原理可知，示踪粒子的浓度是决定PIV-PTV测速精度的重要因素。本文使用一种基于维诺多边形划分的粒子局部浓度评估准则。维诺分析广泛应用于气象学、细胞学和建筑结构领域，是一种特殊的空间划分方法。Monchaux等[21]首先将维诺分析引入到颗粒湍流领域，其后得到广泛应用[22-25]。对于二维平面而言，维诺划分可将包含N个点的平面唯一划分成N个维诺多边形，每个多边形包含且仅包含一个点。对于某一特定的粒子空间分布，维诺划分具有客观性和唯一性。基于这一特性，可以用维诺单元面积的倒数衡量局部粒子浓度。

维诺多边形生成流程如图3所示。通过粒子识别得到示踪粒子的中心点坐标，对点集生成Delaunay三角形网，Delaunay三角形的外接圆圆心是与三角形相关的维诺多边形的一个顶点，连接各顶点即可得到维诺图。

图3 维诺多边形生成流程Fig. 3 Voronoi polygon generation process

用包含单个示踪粒子的维诺多边形面积的倒数来表征当地的粒子浓度，称为DBV（density based on voronoi）密度， 其定义为：

其中，S(pi)为第i个维诺多边形的面积，单位为pixel2。可以看到，DBV密度度量与PPP（particles per pixel）密度度量本质相同。基于每个粒子当地的DBV密度和设定的阈值，可对每个粒子当地浓度进行稀疏或稠密的判定，进一步在粒子稀疏区域应用PTV，在粒子稠密区域使用PIV。然而，对一个非常小的区域应用PTV是没有意义的。若将稀疏或稠密看作是每个粒子的特征，我们希望找到一条稀疏区和稠密区之间的光滑分割线。

1.4 基于高斯核的支持向量机

SVM是一种二分类算法，其基本模型是定义在特征空间上的间隔最大的线性分类器[26]。数据集根据自身特征可分为如图4所示的线性可分、软间隔可分和线性不可分3种情况[27]。

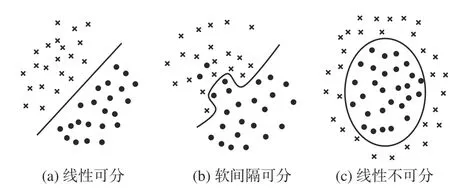
图4 3种数据集类型示意图Fig. 4 Three types of data diagram

以线性可分数据集为例，给定一些数据点，它们分别属于两个不同的类，用X表示数据点，用Y表示类别（Y取1或者-1，分别代表两个不同的类），SVM学习目标便是要在空间中通过间隔最大化策略找到一个最优的分离超平面（hyper plane）。

线性可分问题的处理手段已经非常成熟，而对于非线性可分问题，可通过映射函数将原空间映射至线性可分新空间。映射函数由核函数确定。设H为特征空间，如果存在一个从X到H的映射函数ϕ(x):X→H，使得对所有x1,x2∈X, 函数K(x1,x2)满足条件K(x1,x2)=ϕ(x1)·ϕ(x2)，则称K(x1,x2)为核函数。一个常用的核函数是高斯核：

其中σ为高斯核函数的超参数。SVM中还存在另一个超参数C，C越大则代表模型对误分类的惩罚越大。σ和惩罚参数C的设置会显著影响划分结果，本文选用的超参数基于网格法进行寻优得到，分别为σ= 0.2，惩罚参数C= 0.0023。在实际应用中需要根据具体情况调整，以使得最终的划分符合预期。

2 粒子图像分割

2.1 仿真粒子图像合成

由于真实测速实验中无法获得先验的参考速度场，在仿真测试阶段，为了验证算法的有效性，按照验证PIV-PTV算法的一般惯例，使用人工生成仿真粒子图像进行算法测试。相比以往的仿真粒子图像[28-30]，本文合成的粒子图像具有显著的粒子分布不均的特征。其合成步骤如下：

1）由二维高斯函数分布生成单个虚拟粒子的灰度分布，以制备粒子集备用。粒子灰度分布函数为：

其中，(x0,y0)为粒子的中心位置，粒子灰度等级的峰值强度为I0∈(150,250)，粒子直径dτ∈(2,5)。

2）在大小为512 pixel × 512 pixel的灰度矩阵（第一帧粒子图像）中随机划定部分区域为稀疏区域，其余部分设定为稠密区域。

3）在稀疏区域和稠密区域分别以PPP ＜0.002的密度和PPP = 0.004的密度随机放置粒子，并记录粒子坐标，产生第一帧粒子图像。

4）建立一个512 × 512的标签矩阵，在该标签矩阵中由步骤3定义的稠密区的标签记为0、稀疏区的标签记为1。

5）给定速度场，将步骤3中第一帧图像中的每个粒子按照当地速度进行跨帧移动，产生第二帧PIV图像。

6）在产生的两帧粒子图像中添加噪声，使得生成的粒子图像更接近真实实验图像。最终输出具有粒子稀疏分布的PIV图像对和其对应的标签矩阵。

2.2 模型评价指标IoU

能否正确地划分稀疏区和稠密区，是决定混合PIV-PTV算法表现的关键，为此定义稀疏区交并比（intersection over union, IoU），用以定量评估SVM算法对稀疏区划分的合理性。IoU系数是一种集合相似度度量函数，通常用于计算两个样本的相似度，取值范围在[0,1]。其公式如下：

A∩B是A和B之间的交集，A∪B是A和B的并集。在本文研究的问题中，A代表预设的稀疏区域，B表示SVM划分出的稀疏区域。IoU数值越高表明A区域与B区域重合程度越高，SVM的划分越准确。IoU具有尺度不变性和非负性等特性，在后文，我们将以IoU为评价指标，探究SVM划分稀疏区的表现。

2.3 阈值的选择

阈值的选择会深刻影响划分结果，应充分考虑现有PIV和PTV算法的处理能力。若现有PIV算法要求计算区域密度至少为ρ1才能进行有效的互相关计算，而PTV方法能处理的最高密度为ρ2，则此时粒子浓度的阈值ρ的可选择范围应为ρ1＜ρ＜ρ2。通常情况下，PIV算法要求在一个查询区（32 pixel × 32 pixel）内示踪粒子数目应至少大于3；反之，若粒子数目低于3，则认为使用PTV技术得到的速度场更有参考价值。基于此，本文工作中以DBV密度ρ= 0.003作为临界阈值。

2.4 仿真PIV图像分割

使用2.1节仿真粒子图像合成方法生成的一帧粒子图像如图5所示，其速度呈兰金涡结构。兰金涡的涡核区域为预设的粒子稀疏区，其边界如图6中橙色线条所示。涡心位置为（295, 293），半径a为92，速度分布在极坐标系下表示为：

图5 粒子图像划分Fig. 5 Illustration of particle image partitioning

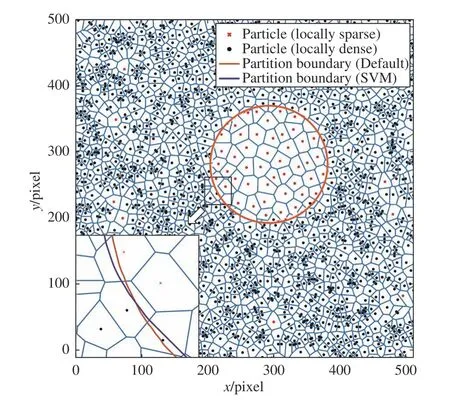
图6 粒子图像的维诺图Fig. 6 The Voronoi diagram of the tracer particles

其中，Γ为涡环量，r为任一点到涡心的距离。

对生成的仿真粒子图像进行粒子识别，并生成维诺多边形，如图6所示。根据维诺多边形计算DBV密度，并以密度ρ= 0.003为阈值对粒子进行分类。图6中，红色点代表该示踪粒子的DBV密度小于设定阈值，即为当地稀疏；黑色点代表该示踪粒子的DBV密度大于设定阈值，即为当地稠密。可以看到，红色点主要分布在图像中心区域，即中心区域存在一个较大的稀疏区，在图像边缘处也分布着许多小的稀疏区。

基于高斯核函数的SVM寻找两类粒子的光滑分割边界。图6中，紫色曲线为SVM划分得到的稀疏区与稠密区边界，橙色曲线为预先划定的粒子稀疏区域的边界。使用公式（5）计算预设稀疏区与预测稀疏区交并比IoU为0.96。基于SVM结果，得到适宜使用PIV和PTV的区域如图5所示。

3 混合PIV-PTV测速仿真分析

基于图5给出的划分结果，对SVM划分出的粒子稠密区使用基于多重迭代的光流PIV算法MILK[31]计算速度场，查询区大小设为32 pixel × 32 pixel，步长设为1 pixel。应用PIV算法计算速度场的结果如图7中蓝色箭头所示。使用基于蚁群优化的混合粒子匹配算法[32]进行PTV计算，该方法可以看作是传统蚁群PTV算法的一个更新，其核心思想是通过改进的蚁群算法来寻求混合目标函数在全局中的最小化解，该方法在跨帧位移较大的场景下表现出良好的鲁棒性[32]。对划分出的稀疏区域应用该粒子追踪算法，其计算结果如图7红色箭头所示。

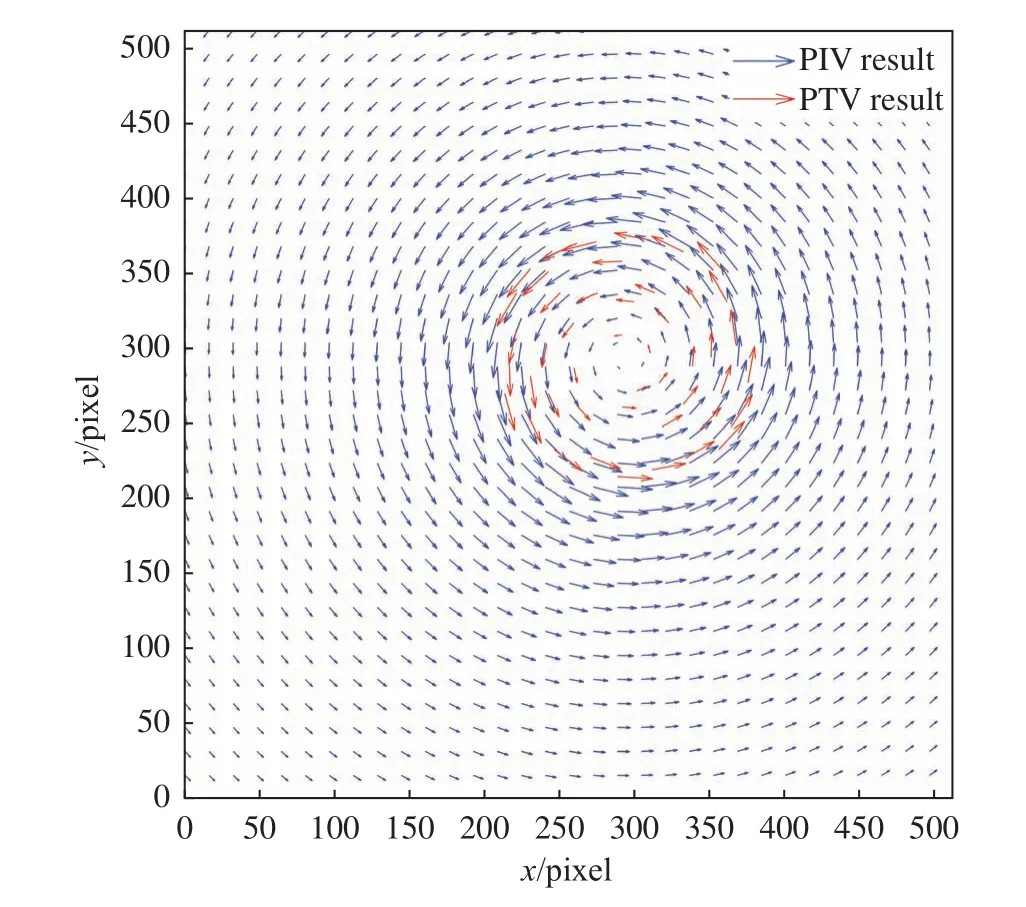
图7 混合PIV-PTV结果展示Fig. 7 Illustration of Hybrid PIV-PTV results

图7中可以看到，PIV算法计算结果与理论速度总体分布具有一致性。图8给出了PIV算法和PTV算法得到的跨帧位移切向分量的误差沿径向r的分布。可以看到，在兰金涡涡核内部，PIV结果的平均误差在1 pixel附近，显著高于PTV的误差（约0.1～0.5 pixel）。在距涡心75～100 pixel半径区域内，PIV算法误差较大，究其原因有两点：一是该区域示踪粒子稀疏，难以进行有效的互相关计算；二是因兰金涡的存在，该区域具有速度梯度较大的剪切流动，平均效应的存在导致PIV计算产生较大误差。而PTV方法适用于粒子稀疏区域，且对速度梯度不敏感，故表现出较低的计算误差。由此可见，分区域分别应用PIV、PTV进行速度场计算是必要的。

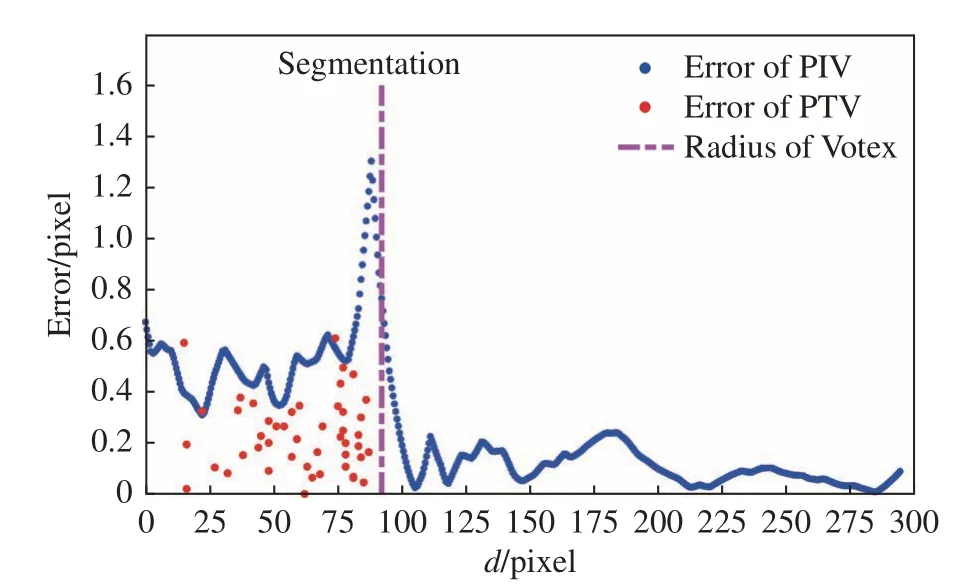
图8 PIV-PTV误差分布Fig. 8 Error distribution of PIV-PTV

4 混合PIV-PTV测速应用实例

在高超声速平板边界层流动中，强剪切流使得示踪粒子难以进入边界层近壁区[33]，导致PIV计算速度存在偏差。在本节中，混合PIV-PTV测速方法被应用于来流马赫数Ma= 6的高超声速平板边界层速度测量中，实验在航天空气动力技术研究院的FD-03高速风洞中进行，实验示意图见图9。如图9所示，模型主要由玻璃平板和转捩带组成。其中，玻璃平板长度240 mm，平板前缘距转捩带10 mm、距模型最前缘60 mm；采用Nd:YAG脉冲式双曝光激光器，该激光器输出能量达600 mJ；使用跨帧CCD相机进行流场拍摄，相机分辨率为2048 pixel ×2048 pixel。实验参数如表1所示。

表1 实验参数与实验工况Table 1 Experimental conditions

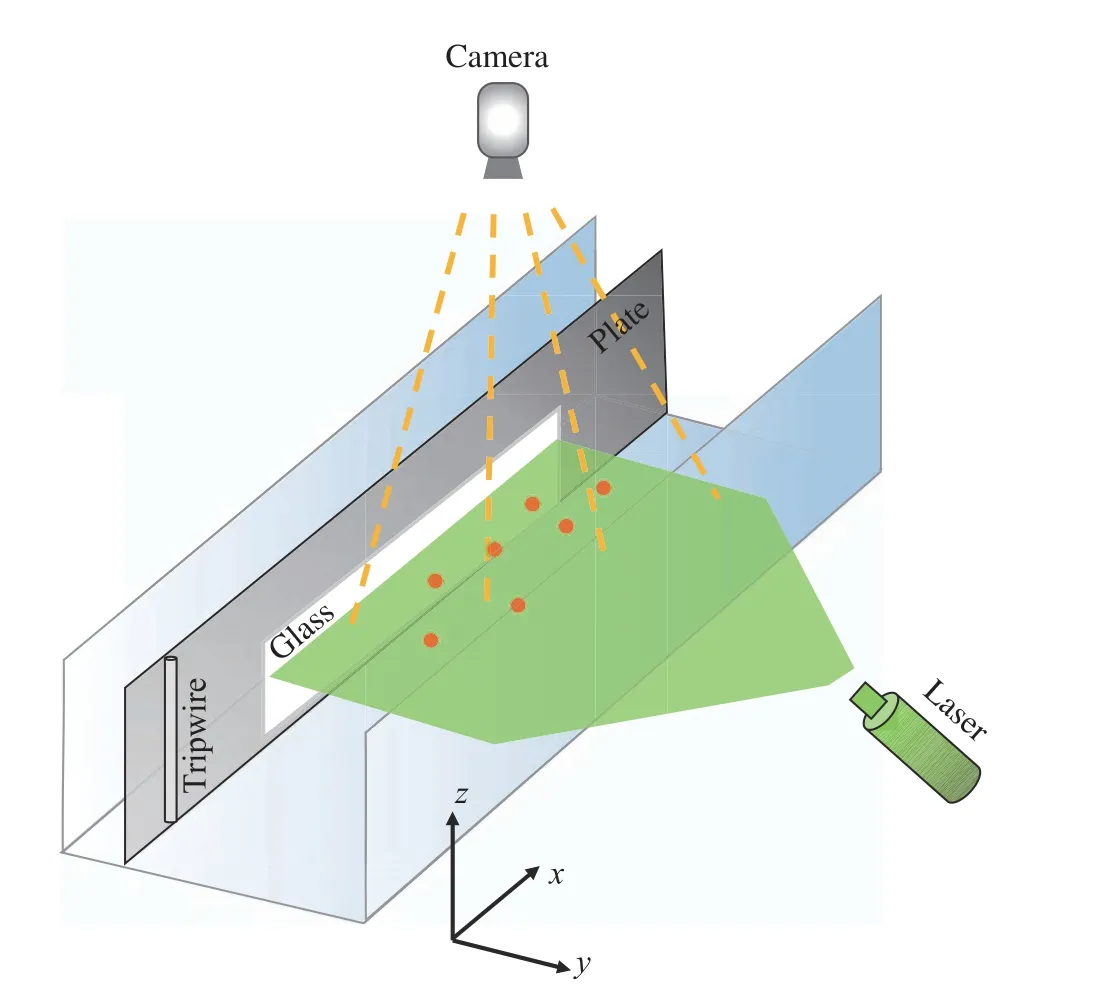
图9 Ma = 6超声速PIV实验示意图Fig. 9 PIV experimental sketch for flat-plate flow at Ma = 6

为了便于算法验证，截取实验图像部分区域进行分析，如图10所示。截取粒子图像底部，靠近壁面且与壁面平行，大小为1024 pixel × 1024 pixel；对应物理空间为11.2 mm × 11.2 mm，成像区域最上游距模型最前沿235 mm，该位置边界层厚度为4.4 mm。

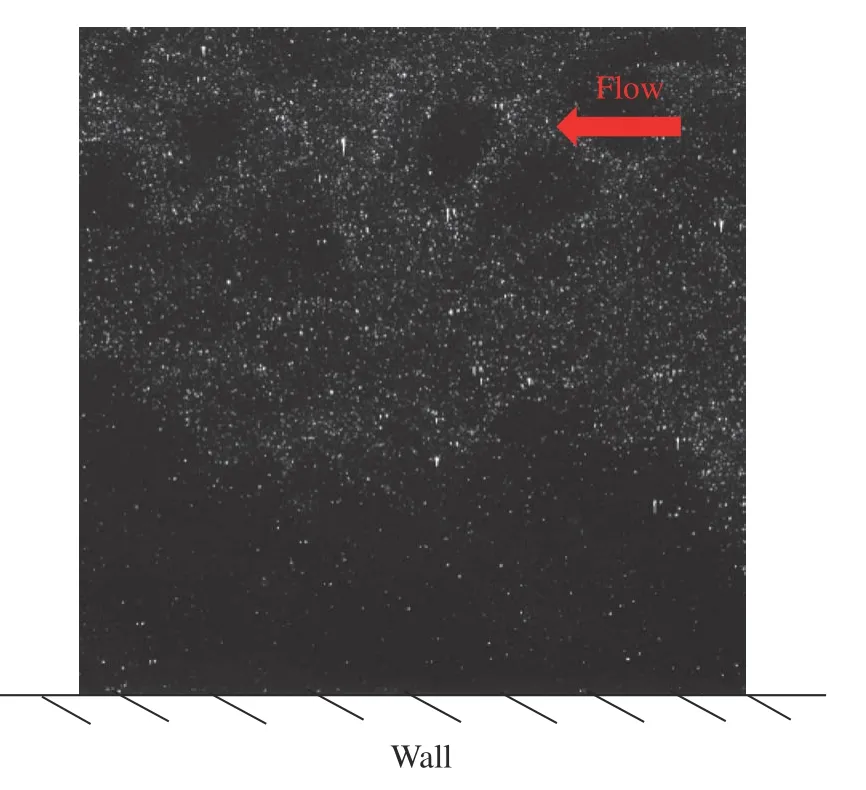
图10 Ma = 6超声速PIV实验结果Fig. 10 PIV experimental image for flat-plate flow at Ma = 6

使用改进的动态阈值法进行粒子识别并进行维诺多边形划分，得到如图11（a）所示的维诺图。计算DBV密度并以密度阈值ρ= 0.003进行二分类，使用基于高斯核函数的SVM进行稀疏区和稠密区划分。考虑到对小区域应用PTV没有意义，故剔除划分结果中面积较小的稀疏区域，得到最终的划分边界如图11（a）中橙色线条所示。

图11 超速平板边界层混合PIV-PTV结果Fig. 11 Hybrid PIV-PTV results for flat-plate flow at Ma = 6

超声速平板边界层混合PIV-PTV测量的瞬时速度场结果如图11（b）所示，其中蓝色箭头为PIV测速结果，红色箭头为PTV测速结果。可以看到，使用基于粒子图像分割的混合算法，可以实现对粒子稀疏区域的分割，进而对近壁区域使用误差更小的PTV算法，从而缓解近壁粒子浓度低带来的PIV测量不确定度高、空间分辨率低的问题。

5 结论

本文发展了一种基于粒子图像分割的混合PIVPTV测速方法，用以解决PIV测速实验中局部区域示踪粒子分布不均匀的问题。算法的基本流程是：首先进行单个粒子识别，对每个粒子计算维诺多边形和DBV密度；设定阈值对粒子打标签，使用基于高斯核的SVM、依据DBV密度对粒子进行分类，从而实现对粒子图像稀疏区和稠密区的分割；对分割出的粒子稀疏区和稠密区分别应用PTV和PIV算法计算速度场，实现混合PIV-PTV测速。仿真结果和高速风洞实验表明，SVM方法可以实现对粒子图像基于粒子分布密度的分割，混合PIV-PTV测速方法可以显著提高粒子分布不均场景下的速度测量精度。

需要指出的是，对粒子浓度分布进行简单的二分类不能总是满足工程的需求，在后续研究中可以发展基于粒子浓度的分级策略，对不同浓度的粒子区域在应用PIV时自适应地使用不同的查询窗口，从而进一步挖掘PIV的后处理潜力。