低真空管道列车关键气动问题研究进展

侯自豪，毛 凯，朱雨建，薄靖龙，申 振，李少伟，*

(1. 中国航天科工飞航技术研究院 磁电总体部，北京 100074；2. 中国科学技术大学 近代力学系，合肥 230027)

0 引言

轨道交通方式变革飞速，磁悬浮与电磁推进的成熟化进一步加快了地面交通方式的革新。高铁长期运营的最高速度约350 km/h，磁悬浮列车克服了接触摩擦，速度可达400 km/h以上。高速运行使得气动阻力占据列车总阻力的80%以上，并产生颇具危害的噪声污染，这极大地限制了列车的进一步提速[1]。为了突破速度瓶颈，研究者们设想采用管道覆盖高速磁悬浮列车并抽取管道内部分空气的手段，在地面上创造出低密度环境，从而大幅降低列车气动阻力，以一种相对经济可行的方式，使得高亚声速（600 km/h以上）乃至超声速的地面交通成为可能（图1）。这一概念被称之为（低真空）管道列车，是一种颇具潜力的未来地面高速交通方式。

图1 不同发展阶段的轨道交通方式Fig. 1 Rail transit modes at different stages of development

管道列车起源较早[2]，但受限于当时技术，这一理念未得到广泛关注。20世纪末以来，得益于磁悬浮技术的飞速发展，众多方案开始论证。国外最具代表性的有瑞士的超级高铁计划Swissmetro[3]、美国的ETT[4]和Hyperloop[5]等，并率先开展了公里级试验线建设和载人试验[6]。国内的有西南交通大学的超高速高温超导磁悬浮交通系统[7]、中国航天科工集团的高速飞行列车[8]等。此外，中国中车、中国中铁、中国空气动力研究与发展中心、中国科学院力学所、中南大学、同济大学、青岛科技大学等单位在各级项目支持下，开展了大量先期探索研究。600 km/h级中车四方常导磁浮和中车长客高温超导磁浮样车相继下线启用，代表了我国在高速磁浮领域具备了工程化能力。2019年我国印发《交通强国建设纲要》和《国家综合立体交通网规划纲要》[9]，明确提出“低真空管（隧）道高速列车技术储备研发”和“推进超大城市间高速磁悬浮通道布局和试验线路建设”。在各方推动下，管道列车系统正逐步从探索论证迈向工程实践阶段。

在管道列车相关的诸多科学问题中，空气动力学问题至关重要。抽除部分空气可以显著降低气动阻力，但高速运行下的低真空减阻与维持低压所需要的成本和管道建设成本之间存在矛盾，优良的气动性能应能允许更加宽容的系统运行参数，从而降本增效。并且，为保持低压环境所引入的长管道为高速列车诱导流动营造了一种极狭长的受限空间，通常会诱发以管内壅塞、激波现象为主导的大尺度跨声速流动，导致气动阻力急剧增加和气动热环境恶化。传统高速列车开域运行获得的成熟经验不能被简单地吸收应用，因此对管道列车流动现象、气动特性的机理分析和规律总结等方面的研究工作，是该领域工程技术开发的重要前提。

本文首先总结低真空管道列车流动的共性和突出特点，按照从全场到局部、从一维至多维的思路，对关键气动问题的研究进展进行逐步深入的介绍，主要包括流动模态、流动特征和气动特性问题。在此基础上，对管道列车全线多车运行这一实际问题加以讨论，力图在气动层面为运行参数的选取给出建议，继而根据当前面临的挑战，展望该领域气动研究未来的发展方向，以期对将来的深入研究提供参考。

1 管道列车基本流动模态

管道列车诱导流动本质上类似“漏”活塞驱动的流动，如图2所示，其中列车尾流结构借鉴了Baccarella对管道内中心体尾流的认识[10]。与经典密闭活塞问题类似但存在不同。对于密闭活塞，即使活塞速度再小仍可产生压缩波或激波扰动[11]，即必然壅塞，而管道列车由于存在车-管泄流间隙和流动再平衡的过程，上述结论不再严格成立[12]。

图2 管道列车典型流动示意图（仅部分波系）Fig. 2 Schematic of the typical tube train flow field

在列车坐标系中，管内壅塞问题能够得到较好解答。气流在列车邻域遭遇的变截面酷似收缩-扩张型喷管，车-管间隙担当喉道的角色[13]。这一思想启发众多研究者采用经典一维无黏喷管流理论预测管道列车流动的模态。整体上，流动可分为两种模态：一种是起动流，表示列车前方的气流可以全部通过间隙（即通流，unchoked flow）；另一种是不起动流，表示气流无法悉数通过间隙并发生壅塞（choked flow），即达到最大质量流量条件，在这种情况下，质量在前方积累并产生压缩波或激波。

研究人员通过一维无黏气体动力学理论获得了通流与壅塞的转变分界。其中，Oh等[14]、张晓涵等[15]通过最大质量流量条件探究了列车瞬间起动所遵循的等熵极限（Isentropic limit，具有亚声速解和超声速解），壅塞模态位于亚声速解和超声速解之间。Zhou等[16-17]、Yu等[18-20]、Bi等[21]、Zhou等[22]、Zhong等[23]还讨论了列车实际缓慢加速起动导致车前已存在正激波的情形，此时通流应满足更加严格的超声速极限解—Kantrowitz极限。在等熵极限和Kantrowitz极限之间存在一双解区，在此区域内，流动既可处于通流模态，也可处于壅塞模态。

但同时应认识到管道列车流动与喷管流动的不同，经典极限理论描述管道列车流动的充分性需要慎重对待。对于喷管壅塞，扩张段流动依据进出口压力比，呈现出多样性，随着背压降低，依次呈现过膨胀（管内正激波、管口斜激波）、完全膨胀和欠膨胀（管口膨胀波）等亚模态[13]，其本质是压力匹配问题。而在管道列车壅塞流动中，上下游依次呈现“车前未受扰动区、前驱激波压缩、列车区膨胀、车后流动、车后未受扰动区”的闭环过程，列车后方流动更趋于复杂，本质是压力、速度、密度多参数匹配的更具约束性的一般黎曼问题。

列车后方流动的复杂性逐渐得到关注。Hruschka等采用理论分析、数值模拟和自由飞实验相结合的方法研究了管内弹丸高速运行（与管道列车流动类似）的流动模态和气动力特性[24]。研究认为，除亚/超声速通流模态之外，管道壅塞尾流存在两种类型：无激波和存在跟随激波。Jang等借鉴Hruschka的思路，指出列车后方流动与喷管扩张段类似，壅塞流动的三维形态大体可分为两类：车尾出现斜激波和斜激波后方出现跟随激波[25]。Hruschka和Jang的理论模型仅考虑了列车尾部与后方远场压力项的匹配，导致其波系认识及模态转换求解不准确且不完整，可适用于在管道阻塞比较小即稀疏波较弱的情况。

进一步地，侯自豪等忽略车尾三维流动效应，通过拆分流场为车前、列车区和车后并依次求解漏活塞驱动激波、喷管流、黎曼间断问题，全面揭示了列车在广泛运行条件下的一维无黏和黏性流动模态[26-27]。图3为列车运行马赫数MT和管道阻塞比β所构成的模态图。研究发现，用无黏等熵极限和Kantrowitz极限来近似评估黏性流动模态仍是合理的。此外，重点发现了壅塞模态下以二次激波（即Hruschka阐述的跟随激波）状态为临界的两种亚模态：二次激波驻定模态和二次激波脱离模态。后续，Li等[28]、宋嘉源等[29]基于无黏理论对二次激波驻定/脱离极限进行求解，获得了相一致的结果，并探讨了一维理论与多维模拟的差异。

图3 管道列车流动模态和转变极限[27]Fig. 3 Tube train flow modes [27]

各流动模态表征的波系结构截然不同。对应于各流动模态，图4给出了一维无黏自相似波系结构示意图[27]。对于亚/超声速通流模态，其流场仅限于列车邻域的等熵流。壅塞模态以前驱激波（S1）和位于列车尾部或后方的二次激波（S2）为基本特征。图4（b）和图4（c）分别为二次激波驻定和脱离亚模态。车前气流经由间隙的降压加速作用形成尾部超声速过膨胀区，并与车后未受扰动气流之间构成黎曼问题，解析发现其解由二次激波（S2）、中心稀疏波（R）和接触间断面（C）构成。一维研究还发现，不同于无黏自相似流场，当考虑摩擦和传热效应时，远离列车的扰动波会被持续损耗并最终消散，在扰动产出与壁面损耗之间达到渐近平衡，以列车扰动源为中心，流动保持稳定结构[27]。通过求解发现，稀疏波和接触间断面在远离列车的过程中被逐渐削弱并消失殆尽。前驱激波在列车亚声速运行时弱化为马赫波，在超声速运行时得以长时间存在，与列车维持恒定的距离同步运行。二次激波的演变可分为3种类型：（1）当列车以低亚声速运行时，二次激波处于驻定模态；（2）当列车以高亚声速运行时，二次激波从尾部脱离，伴随列车而行；（3）当列车以超声速运行时，二次激波持续远离列车并消散。

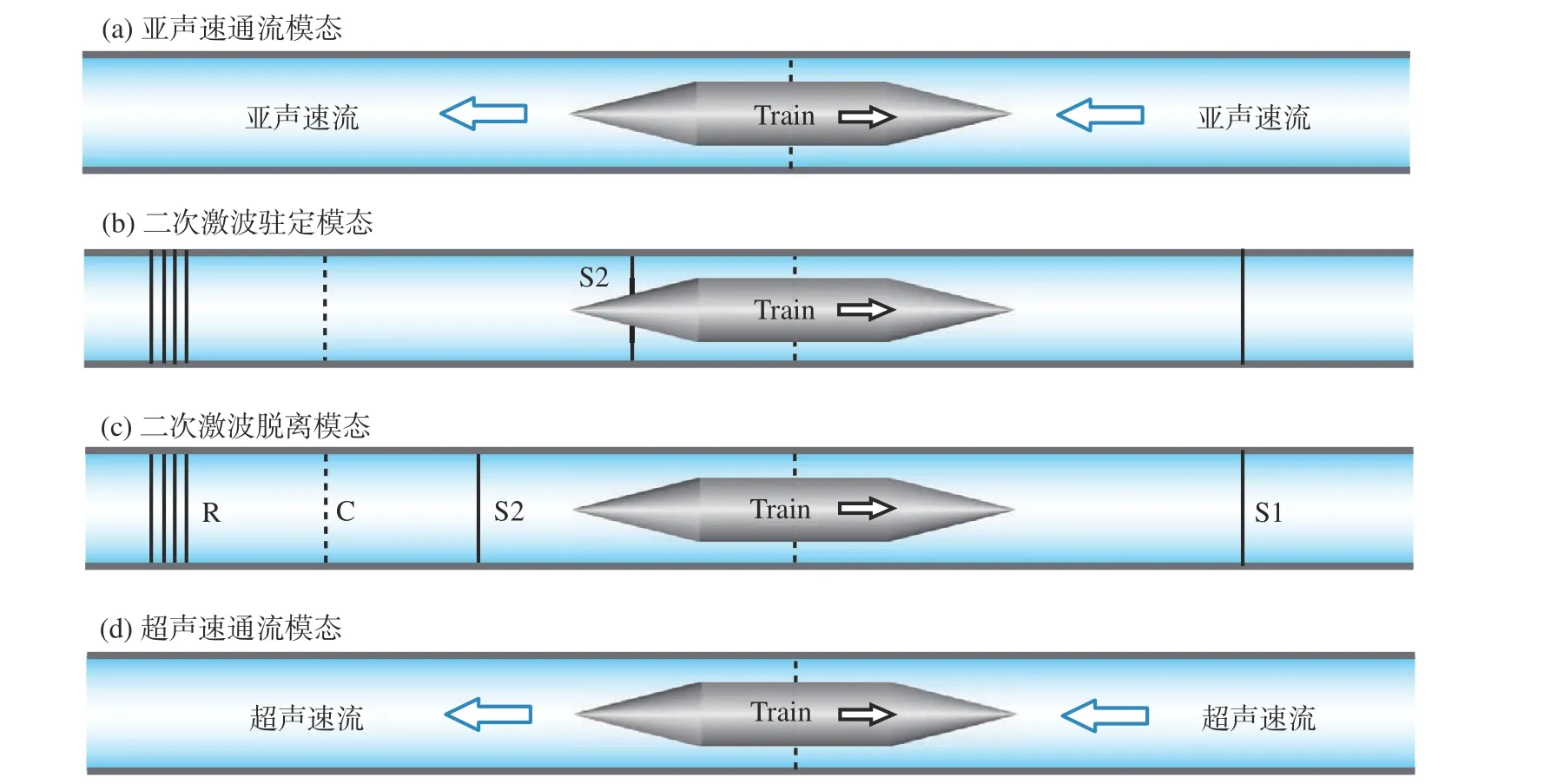
图4 管道列车各流动模态一维无黏波系示意图[27]Fig. 4 Schematic of one-dimensional inviscid wave patterns under various flow modes [27]

一维理论研究实际考虑的是一个宏观的、理想化的物理问题，图3和图4分别给出的流动模态和波系是平均流动假设下的产物，其背后的理论模型并未涉及尾流复杂三维效应。但这种尽可能简单的理论模型往往能够反映流动的本质特征。在基础认识上，将三维效应纳入一维理论有利于建立更准确的流动模态预测模型。

2 管道列车流动特征

工程上更多地期待实现通流模态。研究表明，与列车-隧道流相近，通流模态下气动阻力仍近似与列车速度的平方成正比[14,30]，这种情况一般发生在低速情况下。但在当前主流的管道列车设计蓝图中，列车高速运行并被约束在一定阻塞比管道内，壅塞问题难以规避，是管道列车流动的主导特征，本节从多视角、多维度对相关研究进展进行梳理和归纳。

2.1 壅塞流动的维度和尺度特征

当壅塞发生时，狭长空间中运动激波、稀疏波等扰动的持续传播将极大增加流动的空间尺度和时间尺度。流动能够在数小时跨度内在全程百公里乃至千公里级的长管道内以列车为中心大尺度展开。长程长时流动的特点对研究方法提出了极大挑战。

通过整理大量研究发现此类壅塞流动具有共性，不同流区表现出多样的维度和尺度特征。对于远离列车的流区，流场元素较为单一，流动表现出良好的准一维特征（低维度、大尺度）。对于列车近场，变截面使得流动呈现较复杂的三维特征，尤其是尾流区，但这些三维特征较明显的区域往往只存在于数倍车长（高维度、小尺度）。

因此，目前所采用的研究策略也分成两类。一方面，若立足于全场视角，低真空管道的大长径比性质则使得此类管流问题在轴向上很好地契合了准一维假设。采用降维方法分析大长径比流动问题经济且快速，已经在列车/隧道流[31]、激波管/激波风洞[32-35]、气体炮[36]等研究中得到广泛应用。准一维方法虽然无法精细刻画三维流态，但诸如壁面摩擦和传热等三维现象的一维平均效应可通过成熟的理论模型进行合理描述[32,36]。另一方面，若立足于列车近场视角，流动的解析便需要高维度的计算方法。由于这些方法需要耗费大量资源，只适合截选非常有限的列车邻域复刻多维流动现象。但固有的问题是，车前后扰动长程传播和衰减的过程不应受到有限远处数值边界的影响，短距短时模拟不足以反映实际长程长时流动的本质[37-38]。

可见，管道列车壅塞流动刻画的精细度和完整度难以在单一解决方案中两全。回顾和梳理迄今为止的相关研究不难发现，已有研究往往围绕全场视角和近场视角其中之一来展开，以下分别阐述。

2.2 管道列车全场流动研究

早前，研究人员主要从全场视角出发采用准一维计算方法来认识管道列车流动。多数研究关注列车匀速运行，为了简化计算，通常将全场划分为列车定常近场和非定常远场分别求解，并通过流量匹配条件过渡[37-39]。部分研究探索了一些复杂运行场景，如不同阻塞比、管道长度、加速度等[40]。早期准一维研究主要关注列车低速通流现象，部分研究甚至简化了摩擦和传热过程（均匀摩擦/传热流）。之后，Baron等通过将局部三维流动进行合理的一维化，研究了高速列车以“先加速、再430 km/h匀速、后减速”的运行模式在60 km敞/闭口管道中产生的压力波传播以及气动问题，以较小的计算代价，实现了对宏观流动现象和气动特征的良好复现[31]。

在已有研究基础上，Hou等进一步获得了较完备的考虑变截面、多运动列车以及壁面输运效应的准一维“动”变截面气体动力学模型和数值计算程序[27]。如图5所示，“动”变截面流动不同于通常意义上的等截面或者“定”变截面流动，本质区别在于，由于列车运动，等效流动面积既随坐标变化（变截面）还随时间变化（动截面）。因此需要考虑由于列车运动所导致的通流截面项对流动的影响。在上述气动模型下，研究了单/多列车在通流/壅塞模态、匀速/加速运行模式下的全场流动结构，揭示了通流-壅塞模态转换与迟滞机理，刻画了车前后激波、稀疏波等扰动的长程长时传播、衰减和干扰特性[27,41]。

图5 “动”变截面管流示意图Fig. 5 Schematic of the flow in a variable cross-section tube

准一维计算方法虽对管道列车全场流动的刻画快速且高效，但对列车邻域三维效应的复现尚显不足，或因于此，这种降维方法仍未得到广泛关注。未来，发展精细化的一维数理模型准确复现三维流动的宏观特性，是需要解决的关键问题之一。

2.3 管道列车近场流动研究

2.3.1 实验研究

针对管道列车壅塞流动的实验研究公开报道较少。其难点在于：第一，车与管之间的高速相对运动在实验技术上难以实现；第二，车前后运动激波极大地增加了轴向流动尺度，对实验设备和流场观测方法提出严峻挑战。尽管如此，研究人员也做了有益的探索，主要包括以下3类实验手段。

（1）大型试验线测试。在交通强国战略的大力驱动下，大型磁浮通道试验线研制逐渐拉开帷幕。2020年，西南交通大学立项建设大科学装置“多态耦合轨道交通动模型试验平台”（目标速度1500 km/h）。2021年，航天三院和中北大学联合共建高速飞车实验室，开始建设大同超高速低真空全尺寸试验线（图6，目标速度 1000 km/h），并于近期完成了国内首次全尺寸高温超导航行试验[42]。但受限于当前磁浮推进技术和通道长度，试验线仅可提供中低速通流实验支撑。

图6 超高速低真空全尺度试验线[42]Fig. 6 Full-scale test line for low-vacuum tube trains [42]

（2）风洞实验。风洞设备被认为是进行空气动力学实验最常用、最有效的工具之一。但风洞实验一般应用在开放/半开放空间瞬态内外流环境下，难以适用于管内封闭空间壅塞流动的建立及其长程长时发展，并且其较为单一的气流制造条件难以满足宽速域、广泛真空度条件下灵活的气流需求。

然而通过部分模型简化，仍可发挥风洞实验的效能。相比开放空间，管道列车受管道和轨道的约束，为了厘清“U”型轨地面效应的独立干扰，航天三院对试验车槽道流进行了综合风洞实验研究（图7）。在跨声速风洞中采用测力、测压、压敏漆、脉动压力、尾流纹影等多种测量技术，获得了不同马赫数、攻角以及悬浮高度下试验车的压力分布和气动特性[43]。从部分压敏漆实验结果来看（图8，Ma= 0.5、0.8），试验车上表面压力系数分布表现出典型的跨声速流动特征，在试验车中部出现局部激波和超声速膨胀区。

图7 试验车在风洞中的安装图[43]Fig. 7 Installation of test vehicle in wind tunnel[43]

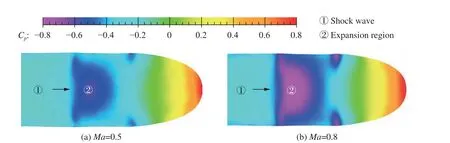
图8 压敏漆实验：试验车上表面部分压力系数分布（车头在右）[43]Fig. 8 Pressure distribution on the upper surface of the vehicle measured by pressure sensitive paint [43]

（3）特种专用实验。为了开展管道空间下高速运行试验，倪章松等在综述研究中报道了一种正在发展的磁浮飞行风洞技术[44]。这是利用管道列车概念结合动模型实验技术提出的一种“体动风静”式新概念风洞设备。该设备有望满足管道列车的高速度和高加速度实验需求，实验马赫数范围可涵盖极低速到超声速范围，并可实现管内压力的大范围调节。

磁浮飞行风洞依托于成熟的高速悬浮推进系统，设备建设成本较高。与之类似地，法德圣路易斯研究所披露了以电磁轨道炮为背景的气炮驱动管道自由飞实验，并系统测试了飞行体气动阻力[24]。此外，韩国铁路研究中心通过简化悬浮推进系统，以气炮替代推进系统、以不锈钢引导线代替悬浮系统，建造了气炮驱动管道列车缩比动模型实验台[45]，用于研究Hyperloop胶囊车在管内高速运行的气动特性。如图9所示，实验台由气炮发射段、加速段（长12 m）、扩散段、实验段（直径0.15 m，长16 m）、制动段、循环管和真空泵系统组成。实验段沿程布置有Kulite传感器和光纤传感器，用于测压和测速。Seo等采用这一设备开展了穿梭舱高速运行实验研究（图10），获得了前驱激波的传播特性，与理论预测值仅存在较小差异。但这种无控制型动模型平台难以保证运行速度的稳定，给实验测量带来不确定性。

图9 气炮驱动管道列车实验台组成[45]Fig. 9 Main components of the experimental equipment driven by the gas gun[45]

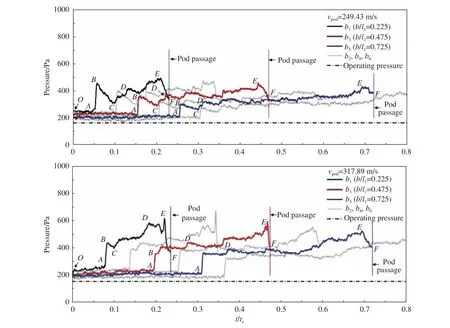
图10 各传感器位置处压力演变[45]Fig. 10 Temporal variations of measured surface pressure [45]

此外，侯自豪等在对管道列车二次激波脱离模态下尾流问题的研究中，通过简化车前壅塞流动的时空尺度，构想出一种远场-近场拼接法：准一维特征良好的远场流区回归至准一维方法，并作为列车近场的边界条件；三维特征明显的近场流区采用实验观测；流区之间通过质量流量条件拼接缝合。在不考虑列车邻域有限区间内车-管相对运动的前提下，以该拼接思想设计了“体静风动” 式低真空管道列车缩比直连实验台（图11）。该实验台由Φ66 mm激波管段和管道列车实验段组成，并以纹影方法观测到在“轨包车”拓扑下列车以1000 km/h运行诱导的复杂尾迹结构，如图12所示，发现尾流以流动分离和激波-边界层干扰为主要特征，并呈现脉动特点。

图11 管道列车直连实验台[41]Fig. 11 Direct-connected platform of the tube train[41]

图12 尾流实验纹影和数值结果对比，速度1000 km/h[41]Fig. 12 Comparison of experimental and numerical results of wake flows with a train speed of 1000 km/h[41]

2.3.2 数值模拟研究

鉴于实验开展的困难，为了获得对列车邻域内局部流动、波系、气动力/热现象进行较高程度的还原刻画，研究人员一般诉诸大规模多维数值模拟。

受计算域和计算网格数量的限制，目前多数研究基于动态分层网格技术，采取了固定列车、赋予气流速度和移动管壁的模式，截取有限的列车邻域流动区间，重点模拟了列车稳定运行状态下的局部定常流动和气动特性。表1显示了部分研究所截取的流动模拟区间和网格数量[16,30,46-50]。另一些研究则基于动网格或重叠网格技术[51-60]，模拟了列车运动状态。

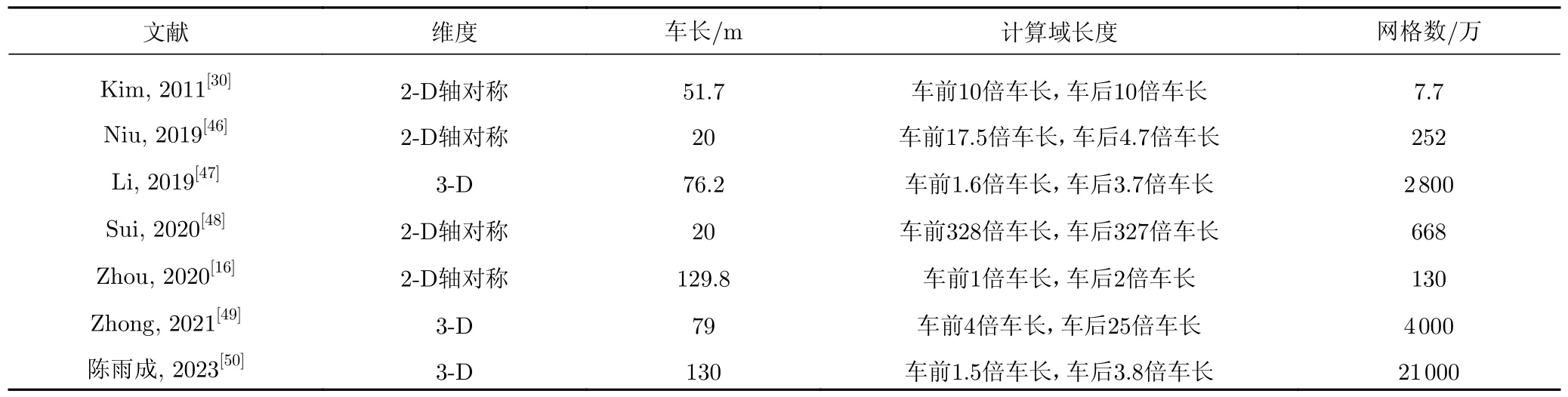
表1 部分研究中截取的列车邻域模拟区间Table 1 Intercepted intervals in the train neighborhood in representative studies

作为典型展示，图13给出了管道列车邻域流动的部分数值模拟研究结果。结果表明，高速运行下管道列车流动往往处于壅塞模态，尾流以外的流区仍保有良好的准一维性质。与图4示意的一维流场相比，相同点是管道内运动型波系定性一致，列车前后方均产生了运动激波；不同点在于列车尾流区域呈现出明显的三维性质，包含了丰富的波系结构，如激波串、流动分离、激波-剪切层/边界层相互作用等。其中，周鹏等采用雷诺平均N-S方程（Reynolds-averaged Navier-Stokes, RANS）模拟方法刻画了二维轴对称流场中列车邻域弓形激波、λ激波、菱形激波等一系列的激波簇结构，包括列车突然起动这些激波结构的产生、发展和演变过程[17,55-56]。Sui等基于改进的延迟分离涡模拟方法（improved delayed detached eddy simulation, IDDES）进行了二维轴对称数值模拟，揭示了尾流中更为细致的激波-膨胀波及激波-激波的马赫反射结构[58]。Zhong等[49]、胡啸等[60]基于IDDES方法，以三维数值模拟方法详细刻画了悬浮气隙尾流区域更为复杂的三维曲面激波产生、传播、反射、干扰和激波-尾涡相干现象。陈雨成等则采用更为精细的网格进行了大涡模拟（large eddy simulation, LES）[50]，研究发现，通流模态下的尾涡区域较大，而壅塞模态下的尾涡脱落受到尾部“X”形斜激波的抑制，在两侧形成双马尾状发夹涡结构，并向下游发展。

图13 部分研究中列车邻域流动数值模拟结果[18,46,48-49,51,60]Fig. 13 Representative numerical results of the tube train near-field flow [18,46,48-49,51,60]

纵观研究历程，近年来所采用的湍流模型和数值方法愈加精细化，所关注的流动结构尺度越发细微，这就要求研究人员在精确度和计算成本之间寻求平衡点。如若关注阻力、压力、温度等宏观参数，从Niu等的结果来看，采用RANS SSTk-ω湍流模型与DDES SSTk-ω的计算结果基本一致[46]，RANS模拟已经具有足够的准确度；而若关注点在于激波、涡流等结构，从黄尊地等的结果来看，RANS、DES和LES方法所获得的喷射器尾流特性均与实验吻合较好[61]，但DES和LES无疑在非稳态流动的精细模拟方面具有更大优势。

以上研究大多集中在单列车稳定运行状态下的基本流动，随着认识的深入，更贴合实际的场景得到关注。如列车进出站引起的管道突扩/突缩效应[62]、管道泄露气动效应[63]、加减速运行和多车运行等。这里着重对短距加减速运行和多车运行进行梳理。

1） 短距加减速运行。Niu等[54]、Bi等[21]模拟了列车以先匀加速、再超声速稳定运行、后匀减速的模式在管内诱导的流场，Zhong等[23]、宋嘉源等[29]则关注了列车先匀加速后匀速的运行模式。其中，Zhong等结合一维理论分析和多维模拟重点分析了列车气动阻力的演变特性，发现加速至大于Kantrowitz极限能够引起流动模态的连续转变：亚声速通流、二次激波驻定、二次激波脱离、超声速通流。由于计算域长度的限制，研究通常采用较高的加速度（如Niu等采用111～444 m/s2，Bi等采用111～146 m/s2），这可能破坏了实际缓慢加速情况下（1～2 m/s2）列车邻域准定常流动假设，与真实的流动有一定区别。

2） 多车跟车/会车运行。Le等研究了多车短距间隔同向运行所诱导的跟车干扰[64]，如图14（a）所示。研究发现，跟车或会车干扰前，各列车均以单列车基本流动为特征。跟车干扰主要分为两个阶段：前车的二次激波/膨胀波与后车的前驱激波干扰，干扰后压缩区前传至头车前方而膨胀区后移至末车后方。但Le等采用的列车间隔较小（43～86 m），与多列车重连场景类似，这实际放大了跟车干扰。伊严严等研究了两车交会所诱导的会车干扰[65]，如图14（b）所示。会车干扰可分为三个阶段：交会前两车前驱激波相互干扰导致阻力陡然增加，交会时两车驶入对车尾流膨胀区导致阻力降低，交会后两车流场及阻力逐渐恢复至单车运行状态。

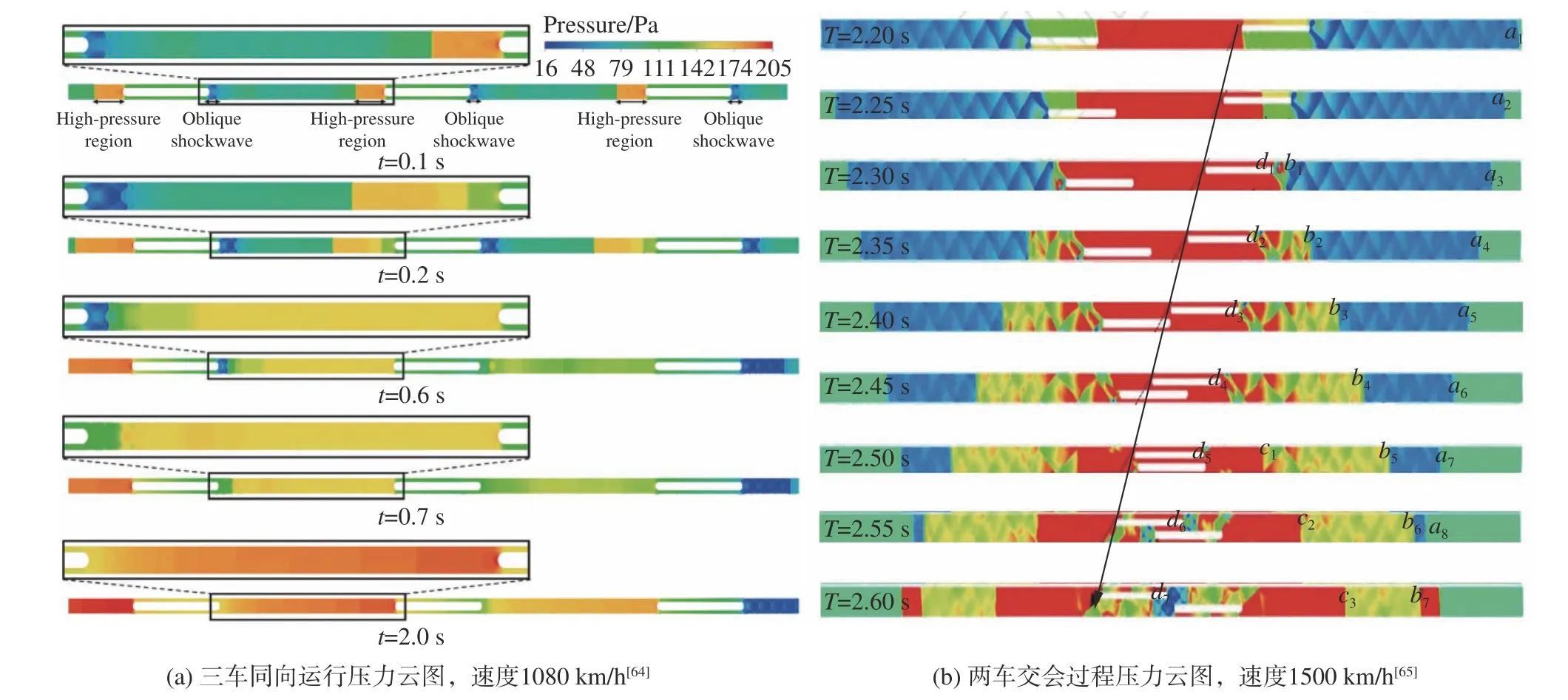
图14 多车运行诱导流动干扰Fig. 14 Flow interactions induced by multiple trains in operation

以上，多维数值模拟虽然对列车近场流动有较高的还原度，但其局限性在于难以实现全程、全尺度模拟，多车续发场景更是给大规模数值模拟带来极大挑战。而前文所述的准一维方法近年来逐渐成熟，并已经在长距离、长时间的大尺度模拟方面展示出应用潜力，诸多在近场视角下难以厘清的问题有望得以有效解决。

3 管道列车气动特性及其调控

综合管道列车全场和近场流动特征来看，在壅塞流动建立、发展和干扰过程中，封闭管道内质量的输运、动量的传递和能量的积聚与耗散跟随管内运动型波系和列车邻域附体型波系呈现出独特的规律，复杂的管内气动环境引起了国内外研究者的广泛关注。以下分别阐述管道列车气动力、热、噪声特性的研究进展。

3.1 管道列车气动力特性研究

当壅塞发生后，列车前方压缩而后方膨胀，这种压力一升一降构成了压差阻力。前方高压气流沿列车外掠，进入环隙，最终汇入列车的低压尾流区。这一过程伴随着气流与列车壁的摩擦作用，导致了列车气动阻力的另一重要分量，即摩擦阻力。此外，还存在侧向力和升力。

当前研究更多关注于列车阻力特性，较少涉及升力、力矩及稳定性分析。大量多维数值研究表明，气动阻力与运行速度、阻塞比、真空度等参数密切相关[14,25,30,46-47,66-71]，且各参数在管道建设成本、运营成本、能耗上相互制约、相互影响[72-73]。此外，环境温度、列车外形、列车长度、悬浮气隙大小、管道断面形状、轨道拓扑等因素也在一定程度上影响了阻力[74-77]。除研究列车受力特性外，张晓涵等[15]、黄尊地等[78]针对以上参数对管壁压力特性的影响也做了系统的研究。

已形成的共识是，气动阻力与真空度、阻塞比的关系较为简洁。可总结为：气动阻力随初始压力增大近似呈线性趋势增加，随阻塞比增大近似呈指数趋势增加，即阻塞比较小时，其变化对列车阻力的影响较小，当阻塞比较大时，阻力急剧上升，并且压差阻力往往在气动阻力中占据主导地位。相比之下，气动阻力与运行速度的关系较为复杂。Hruschka等采用管道自由飞实验系统探究了弹丸在Ma= 0.5～1.5速域内的阻力系数[24]。图15中圆点展示了135车次管道自由飞实验结果，阻力系数呈现出先增大后减小的演变规律，大约在Ma= 0.8处取得峰值。Hruschka对此转折点解释为车-管间隙流动达到完全膨胀状态所致。此外，Oh等[14]、Jang等[25]、Niu等[46]、Kang等[69]的研究中阻力系数演变同样表现出类似的规律，并发现阻力增速在转折点后骤然变缓的现象，分析认为这一现象的产生应与列车尾部激波的出现相关。

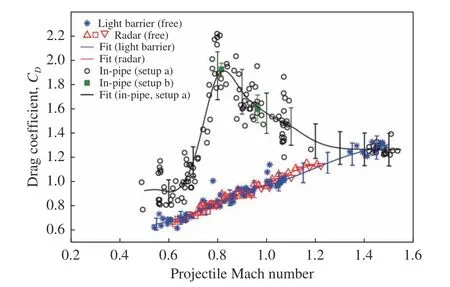
图15 管道自由飞实验测得的弹丸阻力系数（β = 0.08、p0 = 101325 Pa）[24]Fig. 15 In-pipe measured drag coefficients(β = 0.08, p0 = 101325 Pa)[24]

随着对流动模态认识的加深，列车阻力特性与运行速度所处流动模态的相关性逐渐被揭示，阻力系数峰值问题在理论层面获得了更为直观、清晰的解释。Hou等以阻塞比0.25为例，通过一维理论分析呈现了气动阻力随运行速度的变化[27]，如图16所示。研究重点阐释了阻力系数在二次激波驻定/脱离极限处取得峰值的重要分界：当处于二次激波驻定模态时（参考图4（b）），随着列车速度增大，二次激波及其后面的恢复高压区迅速退出车尾，这一过程使得阻力快速增长；而一旦车速超过二次激波驻定/脱离极限，二次激波完全退离尾部（参考图4（c）），它的移动不再贡献于阻力的增长，去除这一因素，阻力的增长反而减缓。根据这一论据，采用图3给出的二次激波驻定/脱离极限理论值能够基本预测到当前多维研究中阻力系数的转折点。后续，Zhong等结合一维理论分析和二维轴对称数值模拟并引入壅塞强度的概念，对加速过程中的阻力系数演变规律做了进一步阐释[23]。

图16 列车阻力和阻力系数随运行速度变化（β = 0.25、p0 = 10132 Pa）[27]Fig. 16 Variations of drag and drag coefficient with the train Mach number (β = 0.25, p0 = 10132 Pa)[27]

3.2 管道列车气动热特性研究

在封闭管道内，气动热的产生、积聚、耗散规律趋于复杂。管道内气动热产生的来源主要有两个，一是壅塞模态下列车前方激波的加热作用，二是高速气流与壁面的摩擦生热作用。在多车续发情况下，多热源叠加还可能会诱导管内热量发生积聚恶化现象。与此同时，管内热量可经由长大管道向外部传递，这又在一定程度上缓解了内流气动热。因此，管道列车所处的热环境主要取决于气动加热与壁面传热的共同作用，其本质是一个动态热平衡问题，一旦失衡，将危及管道列车系统的安全运营。在实际情况中，设备发热、管壁内部热传导、外部环境传导以及太阳辐射的热量等也会参与传热过程，这更加剧了管内热环境的复杂程度。

在产热机理方面，有的从流体熵层分布的角度分析了管内尤其是车周气动热的生成及能量的传递规律[79]，有的从瞬态温度场的角度开展了分析。周鹏等研究了激波簇结构对车周瞬时温升的作用规律[55,57]，并分析了悬浮气隙大小对列车表面气动产热的影响[75]。图17表明，悬浮气隙处具有较强的剪切作用，气流温度较高，并且一旦在列车尾部产生流动分离，气体的高动能转化为高内能，低速回流区的气体也具有较高的温度。宋嘉源等综合列车表面、尾流及管道内部揭示了尾部激波形成、传播对气动产热的影响[80]。通过参数分析，更为全面的认识逐渐建立起来。其中，张俊博等引入了车载设备发热因素研究了不同运行速度、阻塞比和真空度对管内热效应的影响[81]。Sui等、Bao等分别针对阻塞比[48]、真空度[58]、初始温度[82]等参数对列车尾部气动产热的影响开展了更为详尽的研究。余秋君等比较了通流与壅塞模态下气动热特性的差异[19,83]，指出壅塞效应造成了列车表面出现局部加热/冷却现象。针对不同流态，胡啸等进一步基于本征正交分解提取出流场重要相干结构并分析了温度场的非定常特性[84]。

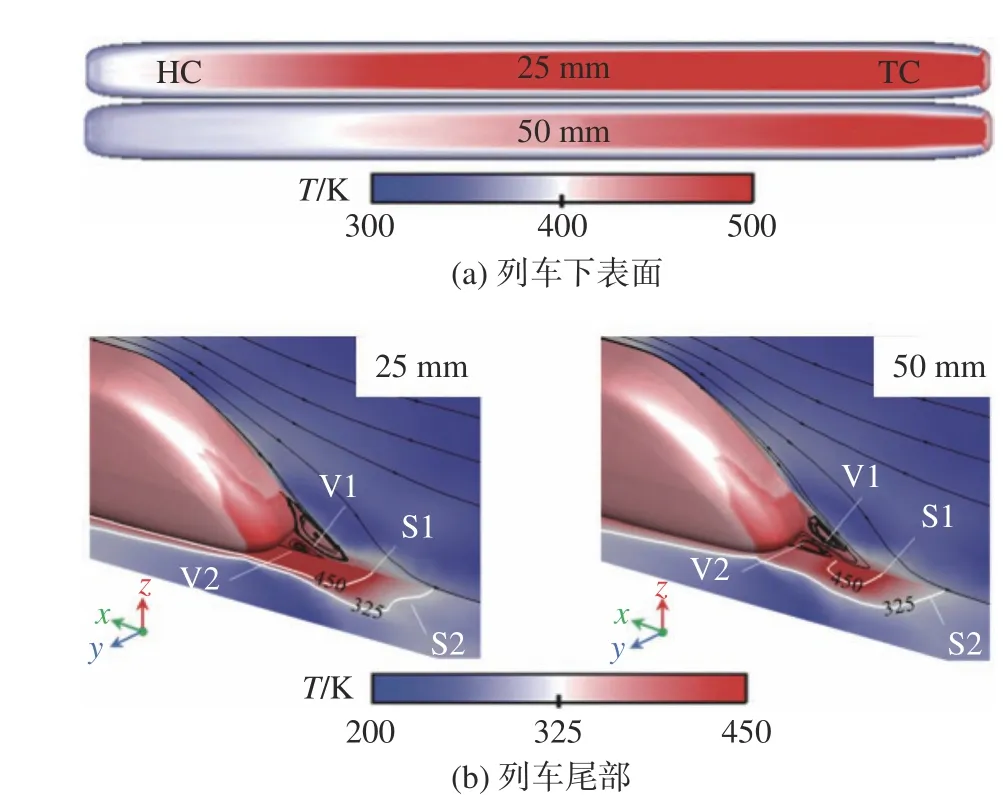
图17 不同悬浮气隙下列车下表面和列车尾部温度场 [75]Fig. 17 Temperature distributions (a) on the bottom surface and(b) in the wake under different suspension air-gaps [75]

在气动热演化方面，Baron等将管内流场简化为一维流动，并忽略管壁传热，通过计算列车长距离运行发现车周温度峰值高出初始值约100 ℃[31]。贾文广[85]、董晨光[86]研究了管内长时间运行的热动力学特性和传热机理，发现随着列车持续运行，车表面最高温度趋于稳定，并指出多车运行发车间隔应合理控制，若空气来不及降温，长时间运行在管道内将积聚更多的热量。

上述研究大多基于绝热壁假设，即不计管壁的对流传热效应，仅单列车运行所计算的管内热环境已经颇为严酷。但实际上，空气与壁面间的热交换至关重要，是管内热环境能够维持热平衡的关键因素。因此当前普遍关注的问题是，随着多车续发持续注入能量，管内是否会出现气动热积聚现象并累积起较高温度。朱艳峰在对低压长大隧道高速运行热效应研究中，综合考虑了空气-壁面对流传热及围岩热传导过程，对多车运行气动热问题进行了初步探究[87]。研究发现，在隧道壁绝热条件下，隧道内每小时通车六列（350 km/h）产生的热量使得隧道内近壁面温度上升5.6 ℃，但若此时考虑壁面传热，多车续发1 h后，隧道内温度几乎恢复至初始值。后续，侯自豪对低真空管道列车全线续发模式下的热环境开展了准一维研究[41]，在第4节中对此做进一步阐述。

3.3 管道列车气动噪声特性研究

研究人员针对高速磁悬浮列车明线运行诱导的气动噪声问题开展了较完备的研究，取得了丰富的成果，但封闭管道内的列车气动噪声问题与之存在显著差异。

在气流壅塞和管道效应的综合作用下，管道内流场表现为强非定常特征，尤其是列车尾流区存在一系列复杂的激波和旋涡结构[49-50,60]，导致气动噪声的产生机理与传播过程错综复杂。一方面，尾流区两侧形成双马尾状的发夹涡，车体与轨道之间的间隙存在周期性的细小涡，如图18所示，不同尺度的涡结构相互掺混会激发强烈的四极子噪声源；另一方面，激波与旋涡相互作用，可诱导激波波阵面和旋涡发生变形及强度变化。这些因素对边界层黏性区将造成显著影响，伴随着脉动压力幅值的增大，气动噪声的辐射声能得到强化，诱导产生强烈的激波-涡波干扰噪声[88]。

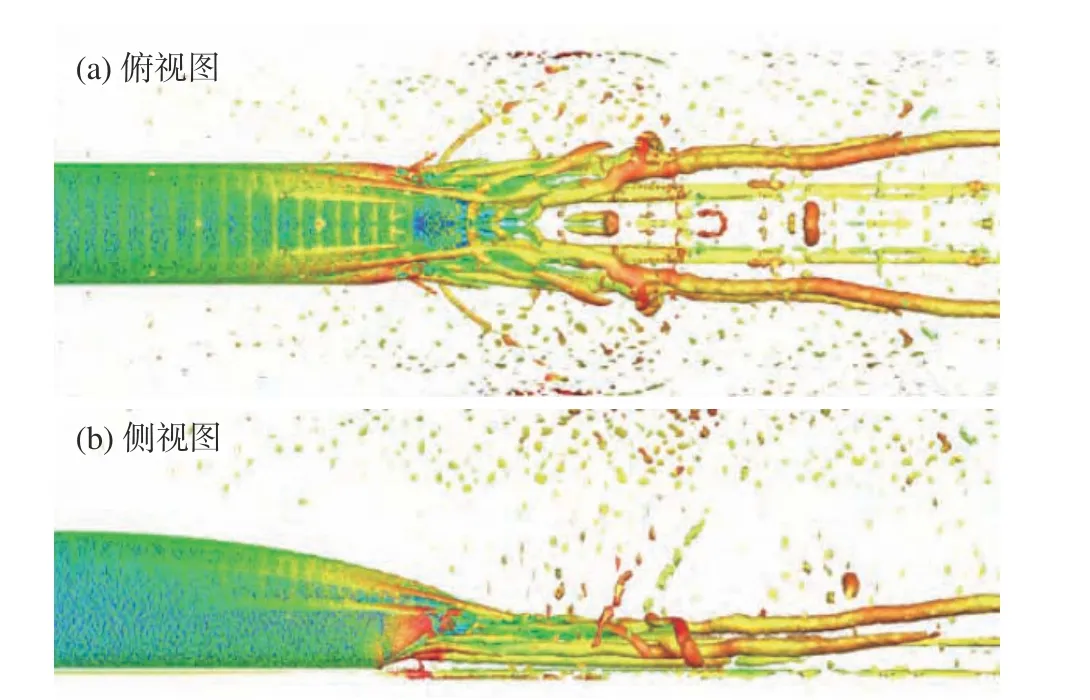
图18 管道列车尾流区Q判据涡结构云图[50]Fig. 18 Vortical structures illustrated by the Q-criterion in the wake of a tube train [50]

针对上述问题，刘加利等采用偶极子噪声源和四极子噪声源模型率先研究了列车速度、阻塞比和真空度对列车气动噪声源的影响[89]。结果表明，当速度为600 km/h时，偶极子噪声源占据主导地位，并且偶极子和四极子噪声源随着阻塞比和管内压力的增大而增大。此外，当高速列车在管道内运行时，声波在管道内的传播过程耦合了气动声学和管道声学，并受到管壁和车体的多重反射、叠加，形成混响环境，使得噪声水平远远大于列车明线运行场景[90]。目前公开文献还未有针对列车气动噪声与长大管道声学耦合效应的研究，这一问题需要加以关注。

3.4 管道列车减阻、降热、降噪研究

面对管内壅塞导致的复杂气动环境，进一步的减阻、降热、降噪策略尤为重要。减阻降热相关研究主要从以下几个方面开展：

1） 优化列车外形。Zhou等[22]、Chen等[91]、Zhang等[92]、Niu等[93]比较了不同的简单列车头尾外形对列车气动力、管内气动热的影响，如锥形、半球形、半椭球形等。Braun等[94]、Opgenoord等[95]针对Hyperloop水滴流线型外形进行了优化，发现通过延迟列车表面层流转变至湍流可小幅降低阻力，通过抑制尾部的流动分离可缓解局部气动热。Yang等通过高效建模方法对已有的三维外形进行了多目标优化[96]。

2） 设置管路横通道、车身通道。Jia等[53]、Hu等[59]通过设想在双管线之间增加旁路横通道以贮存和回流车前高压高温气流，从而达到降低前后压差和降热的目的。后续，Jia等系统研究了横通道间隔、宽度对气动力/热环境的影响规律[97]。Hu等的研究同时指出横通道会对单车和会车运行引入周期流动，带来明显的低频振荡的侧向力[59]。Zhou等模拟了车身开有轴向、径向通道的情况，从前至后流量增大从而缓解了壅塞强度[98]。

目前，降噪研究相对较少，刘加利等指出应在成本允许范围内，尽可能降低阻塞比和管内压力[89]，并对外形进行优化设计[99]，以降低气动噪声。

4 管道列车全线多车运行参数选择

随着方案论证的深入开展，全线多车运行成为工程化阶段的热点问题。而管道列车运行参数的合理范围还不明确，比如运行速度、阻塞比、真空度等，它们共同表征着管道列车的运行潜力、建造和运营成本。通过解耦上述复杂问题，首先考查这些参数对于空气动力学效应的影响，有望获得关键参数选取的范围。基于前文对气动研究进展的梳理，本节依托准一维方法在大尺度模拟方面的优势，对管道列车全线多车运行问题开展简要讨论，以期给出列车运行所处流动模态（由运行速度和阻塞比表征）、发车间隔、全线运行模式的合理选择。

4.1 列车运行速度和管道阻塞比

已有研究往往通过离散工况测试，获得单车气动特性随运行速度和阻塞比的演变规律。图19整理了部分研究所测试的工况及模态区间，如图中数据点所示。调研发现，众多研究更加关注中高亚声速运行速域和阻塞比0.2～0.5范围。通过前文归纳的各流动模态下的流动特征和气动特性，我们给出运行速域和阻塞比选取的建议。

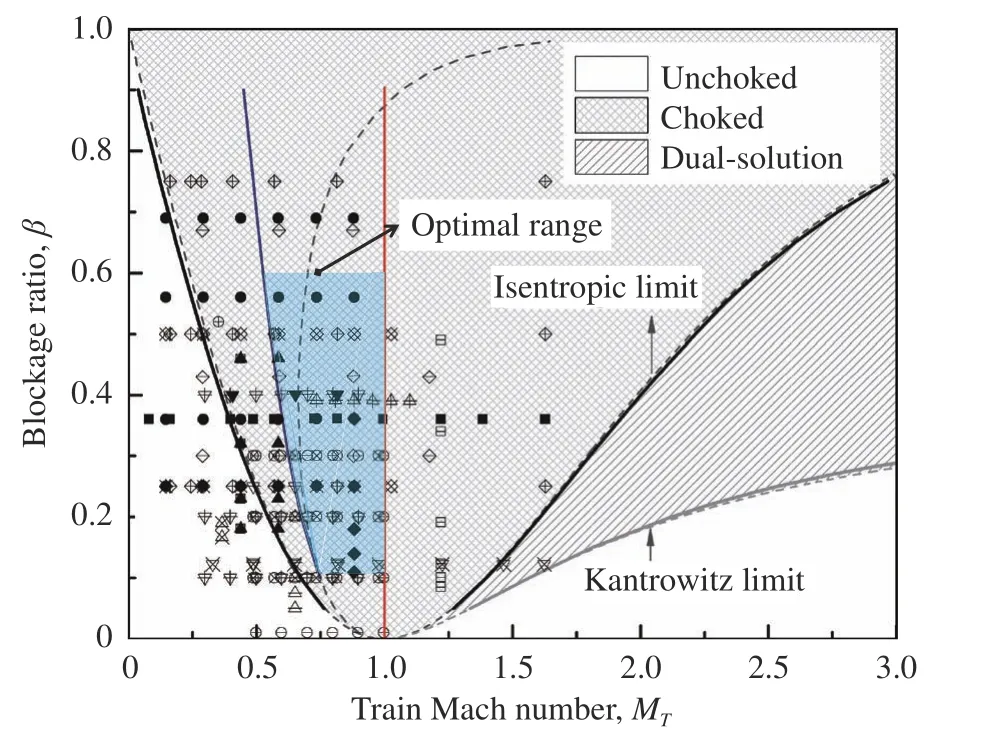
图19 部分研究所测试的速域和阻塞比范围Fig. 19 Train speeds and blockage ratios tested in representative studies

据报道，美国Hyperloop方案的目标时速是1220 km/h，中国航天科工高速飞行列车的目标时速是1000 km/h。对于运行速域，我们认为列车运行在亚声速的二次激波脱离区间（图19中蓝色涂抹区域，大体对应Ma= 0.53～1.0）具有气动层面的合理性，同时又符合工程期望。

以上选取具有三方面依据。一是车体-波系干扰流场简洁。二次激波驻定模态意味着车尾始终裹挟着一道激波（三维流动中不以严格的正激波形式存在），倾向于复杂化运行环境并产生激波诱导车体振动、噪声等问题，二次激波脱离模态相比之下则具有本质上的优势（参考图4）。二是列车运行性价比高。二次激波脱离区间的阻力增长平缓，这意味着进一步增速的代价相对小（参考图16），但过高的超声速运行仍会产生较高的阻力。三是会车干扰相对较弱。前文表明超声速运行情况下前驱激波长时间存在，而亚声速运行情况下二次激波长时间存在，这两种情形下亚声速运行较优。因为列车下游超声速流动（列车坐标系）可以阻隔或弱化会车后二次激波相干对列车的影响，而会车前出现的前驱激波相互作用却较容易影响到列车区，应尽量选取前驱激波较弱的区间。

对于阻塞比，建议管道列车运行在中等程度阻塞比（0.1～0.6）的范围内，更高的阻塞比带来阻力的急剧增加和严峻的气动热环境。但同时考虑到经济性，不建议采用较小的阻塞比，这势必增大管道建设成本。

4.2 多车发车间隔

研究表明，黏性壅塞流场在输运效应的充分作用下，在列车坐标系中趋于稳定[27]。由列车所引起的主要扰动最终被限制在列车前后一定区间，如图20所示。该扰动区由列车前的压缩区和列车后的稀疏区组成。通过壁面摩擦和传热的损耗，压缩区和稀疏区向远场状态渐近收敛。若前驱激波仍然存在，其将是压缩区的前沿；同样，若二次激波存在并脱离，二次激波将是稀疏区的后边界。以此可评估两个扰动区的空间尺度Lfront和Lback。

图20 管道列车上下游扰动区示意图Fig. 20 Front and back disturbed zones of a train

图21（a）以阻塞比0.25、初始压力10132 Pa为例，给出了不同运行速度下的压缩区及稀疏区的尺度。研究发现：一方面，随着运行速度增加，压缩区缩小而稀疏区扩大，当超声速运行时，压缩区以前驱激波为锋面继续收缩，直到进入超声速通流；另一方面，当列车处于低亚声速且二次激波驻定于列车尾部时，稀疏区还未暴露于列车区外。随着运行速度提高至高亚声速时，二次激波与列车分离，且与列车之间的稀疏区增大。当超声速运行时，二次激波不复存在，稀疏区继续增长。总的扰动区尺度在声速极限取得最小值。

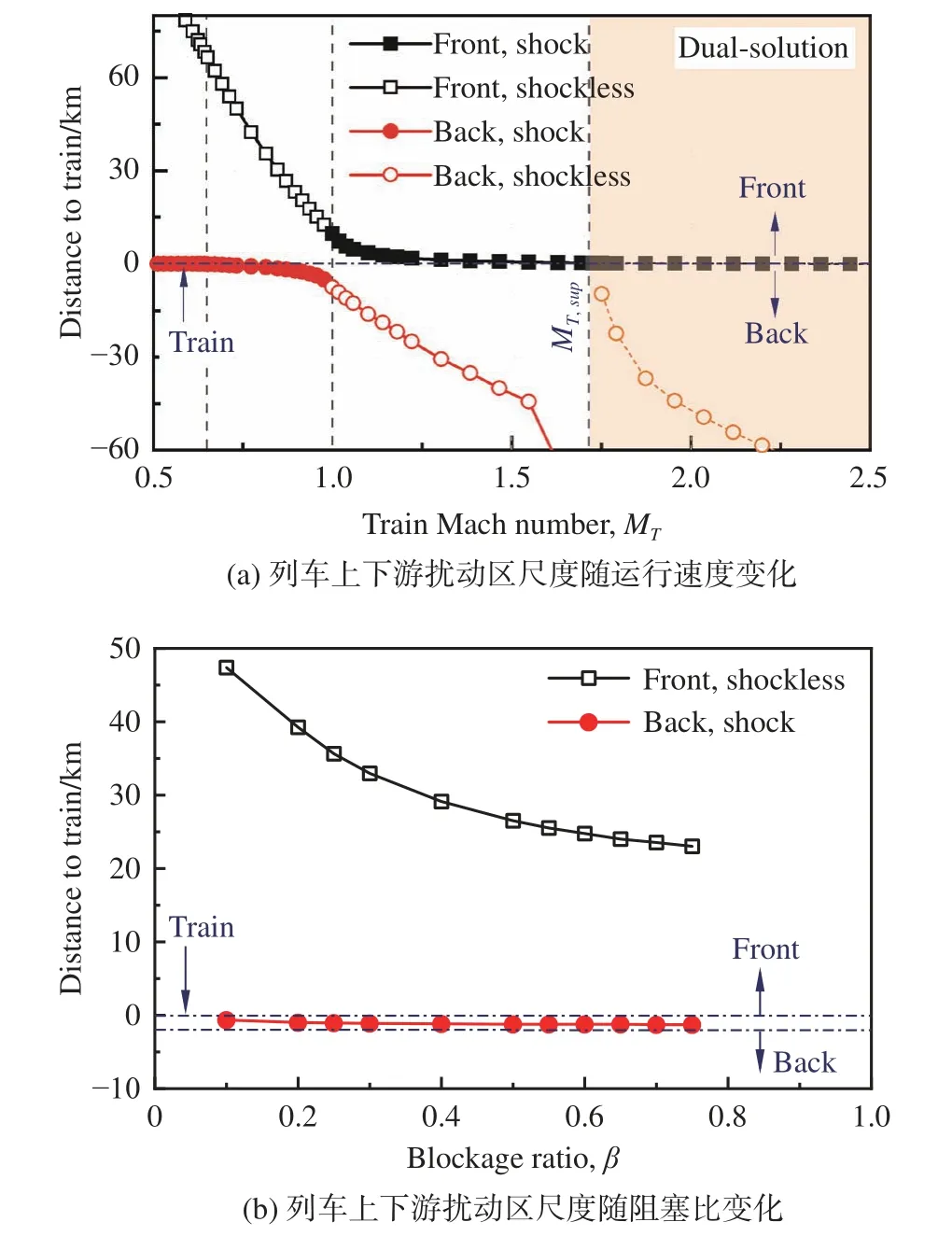
图21 列车上下游扰动区尺度[27,41]Fig. 21 Length scales in the front and back disturbed zones [27,41]

进一步地，图21（b）固定运行速度1000 km/h给出了列车扰动区尺度随阻塞比的变化。压缩区尺度与阻塞比大致成负相关，并且缩减速率逐渐变缓；下游稀疏区则与阻塞比大致成正相关，但基本位于0.6～1.3 km区间。

评估单列车扰动区尺度具有实际意义。对于多维数值模拟而言，上述结果响应了Hammitt的研究结论[37-38]，短管短时模拟不足以反映长程长时管道流动的本质，较完整的多维模拟应考虑容纳上述扰动区或关键区域的尺度。对于管道列车设计而言，正需要这些基本参数作为依据，来优化多车运行场景下发车间隔。从规避列车间气动干扰的角度来讲，前后车间隔至少应为压缩区和稀疏区尺度之和，则最小发车间隔可简单计算为Δtmin=(Lfront+Lback)/utrain。

例如，对于运行速度1000 km/h，当阻塞比为0.5时，压缩区尺度约为26.5 km，稀疏区尺度约为1.2 km，发车间隔至少应为100 s；当阻塞比为0.2时，压缩区尺度约为39.2 km，稀疏区尺度约为1.0 km，发车间隔至少为145 s。这说明高铁的发车间隔（一般大于10 min）乃至地铁发车间隔（5 min左右）基本能够满足管道列车的发车间隔条件。

4.3 全线运行模式

双管单线运行和单管双线运行是当前主流的长距离往返运行方案（图22），高阻塞比单线管道同一截面仅容纳单列车通过，低阻塞比双线管道可容两列车通过。其中，Swissmetro和Hyperloop方案均主张双管单线运行。本小节根据前文所选取的运行参数区间，并结合准一维研究所得结果[41]，对多车全线运行问题进行讨论，同时依据这一实际问题佐证选取参数的合理性。

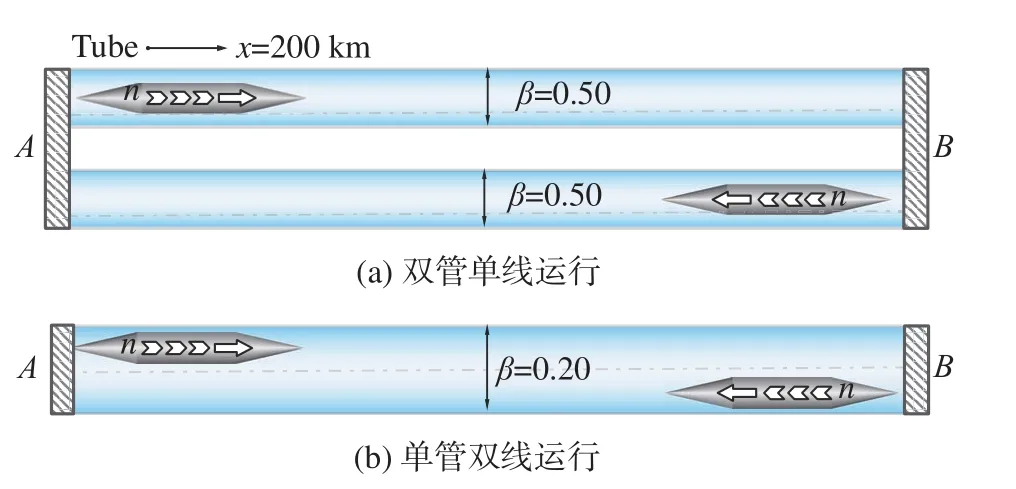
图22 多车运行场景Fig. 22 Scenarios of multiple trains running in a tube

作为典型案例，单线管道阻塞比假定为0.5，双线管道阻塞比为0.2，两车站（A和B）间的距离取200 km，列车巡航速度为1000 km/h，加速度为±1 m/s2，列车从两车站往返发车，发车间隔取5 min。不同于Swissmetro方案主张的地下管道，此处考虑地上管道，将管壁边界简化为理想等温壁。

4.3.1 双管单线运行模式

对于双管单线运行，上下半支反向发车使得流动具有中心对称性，图23仅展示上半支右行车的流场压力和温度x-t图。

图23 双管单线运行流场压力和温度时空图 [41]Fig. 23 Spatial and temporal evolution of (a) pressure and (b) temperature in the case of twin tube[41]

结果表明，由于长大管道摩擦和传热耗散的耦合作用，远离列车区域的气流压力、温度均逼近管道内初值，峰值区域主要集中在列车前方约5 km范围。匀速巡航阶段列车前后的壅塞流场与理论分析一致，以近乎完全衰减的前驱激波和位于车后恒定距离的二次激波（距列车较近，未明显展示）为基本特征。全流场以列车邻域流动为基本单位跟随列车轨迹呈现循环分布。这说明，发车间隔5 min（折合车间距约83.3 km）是合理的，能够有效弱化甚至避免前后车之间的气动干扰。

对右行第1、5、10、15、20列车气动阻力进行考查（全程以巡航速度折算阻力系数），结果见图24。相比01车，后续的发车在稳定运行段的阻力仍基本呈线性增加，这主要是由于偏向一侧的多车续发倾向使得气体从发车侧向另一侧累积压缩，形成左侧稀疏而右侧稠密的整体分布特点。

图24 双管环线运行列车阻力演变 [41]Fig. 24 Temporal evolution of the drag coefficient in the case of twin tube [41]

4.3.2 单管双线运行模式

图25给出了单管双线运行准一维流场压力和温度x-t图。全场特征以列车轨迹及其周围的单车运行准定常流场为基本单位呈现“网状”，列车前存在近乎完全衰减的前驱激波，列车后存在伴行的二次激波。对于会车细节，与伊严严等[65]给出的二维会车干扰流场（图14（a））定性一致：交会前，前驱激波在两车之间来回反射导致会车节点出现局部高温、高压；短暂交会时，两车由对车前方驶入对车的以二次激波为边界的低压区；两车交会后驶离对车低压区，并重新建立起定常壅塞流动特征。

图25 单管双线运行流场压力和温度时空图 [41]Fig. 25 Spatial and temporal evolution of (a) pressure and (b) temperature in the case of train crossing [41]

会车过程的高低压变换引起了列车气动力载荷的强烈波动。如图26所示，与流场对应，气动阻力先是上升至较高水平，而后迅速降低并恢复至稳定状态。匀速阶段的会车干扰可在短时间内产生约五倍的气动阻力。同时，列车交会导致会车点x= 100 km处的高温峰值超过500 K，局部热环境较为严苛。但整体看来，随着发车数量及运行时间的累积，管道内大部分区域的气动热仍不会积聚并趋于恶化，这主要得益于长大管道等温壁充分散热，也合理化了地上高架桥式管道方案。

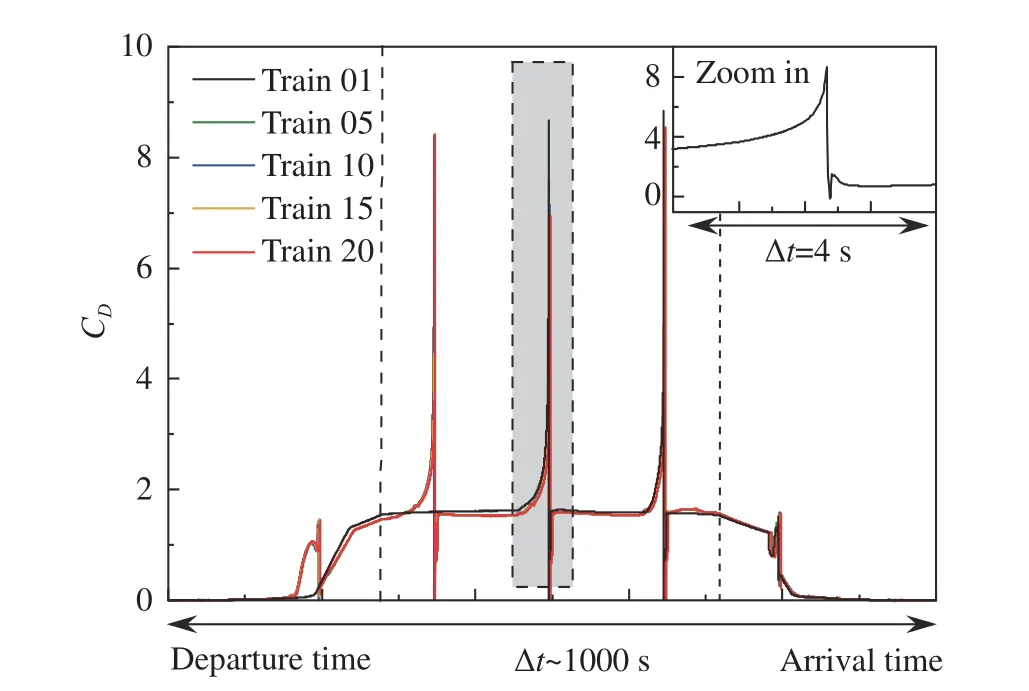
图26 单管双线运行列车阻力系数演变 [41]Fig. 26 Temporal variation of the train drag in the case of train crossing [41]

可见两种运行模式各有优劣，高阻塞比单线管道往往经受全程不稳定的高阻力和较弱气动干扰，而低阻塞比双线管道能够缓解阻力但引入会车干扰。实际工程中，还应综合可实施性和经济性做进一步讨论。

5 研究趋势与展望

当前，低真空管道列车系统的发展正处于迈向工程化阶段的关键环节，其可行性、经济性和应用潜力还存在争议，破除这些疑问需要对其中的关键问题进行系统、完备的研究。管道列车空气动力学研究面临的挑战仍在于：列车高速运行所诱导的以管内壅塞现象为主导的复杂跨声速流动，具有多尺度、多维度、多运动列车的复杂特征，表现出强非定常和非线性物理过程，并且实际应用中系统参数多样且千变万化。这已成为当今制约管道列车设计的关键瓶颈问题，相关研究方法单一，流动机理认识不足，调控手段匮乏。建议从以下几个方面开展深入研究：

1） 多尺度、多维度管道壅塞流动的高效计算、实验方法。准一维方法是对全场特征进行模拟的重要手段，而多维方法对于列车近场的分析又不可替代，两种方法分别已经在“高效性”和“精确性”特点上获得了长足的发展，但目前二者仍被割裂。如何多视角全面认知壅塞流动问题，并对之进行有机结合互补是需要考虑的关键问题。与多尺度模拟研究遥相呼应，地面模拟设备的发展和能力的拓展为管道列车苛刻流动条件的实现提供了可能。比如“体动风静”式磁浮飞行风洞、气炮动模平台和 “体静风动”式管道列车直连实验台等已展示出具有精细化测量的潜力。新的研究方法为揭示底层物理机制提供强有力的支撑。

2） 多车运行流动干扰。未来运营场景中，列车长距离的往返运行、续发运行将成为常态，流动干扰是其中的基础问题，包括列车与轨道的地面效应干扰、列车进出站干扰、列车途径横通道/道岔干扰、复压过程干扰、跟车/超车/会车干扰等问题。诠释这些问题的机理，可为同类管道列车流动问题提供共性参考价值。

3） 多车运行管内气动热环境。低真空管道为密闭环境，管内对流传热、管壁热传导和设备产热等极大复杂化热环境，简单的绝热壁或等温壁模型不足以描述管内气动热现象。同时，未来运营将乘客引入交通系统内，使得管道内气动热评估和热管理成为不容忽视的问题，在系统的设计阶段就需特别关注。

4） 长大管道气动噪声产生及传播机理。低真空管道列车高速运行时，气动噪声将成为主要的噪声源。由于流动分离、激波-涡波干扰以及管道壁面声反射现象的存在，管道内气动噪声的产生机理和传播过程较为复杂。国内外相关研究匮乏，需发展气动声学与管道声学耦合研究方法，揭示气动噪声产生及传播机理，为低真空管道列车气动噪声控制奠定基础。

5） 管道列车减阻、降热、降噪技术。管内壅塞现象带来较为严峻的气动环境，在经济成本的限制下，密封性、低气压、大尺度等特点使得常规减阻、降热、降噪技术未必适用。因此，探索相关技术和提高效能的途径需求迫切，是突破“认知”至“调控”的关键一环。

近些年来，磁浮推进技术的飞速发展和交通强国战略重大需求的驱动，为低真空管道列车的发展提供了难得的机遇，也带来了新的挑战。低真空管道列车的“科技狂想”正在逐步实现，其应用潜力的挖掘仍有漫长的路要走。期望本文阐述的管道列车空气动力学基础科学研究，能为低真空管道列车相关技术创新注入动力，推动低真空管道列车研制和工程应用，助力我国引领未来超高速轨道交通领域的发展。