轴对称Boltzmann模型方程统一算法与空天飞行环境喷管流动模拟

李 凡，李志辉，*，李中华，罗万清，陈爱国

(1. 北京流体动力科学研究中心，北京 100011；2. 国家计算流体力学实验室，北京 100191；3. 中国空气动力研究与发展中心 超高速空气动力研究所，绵阳 621000)

0 引言

轴对称流动广泛存在于自然界，无论是在轨航天器还是微纳米器件中，都有很强的工程应用背景。针对轴对称流动Boltzmann模型方程数值模拟，如果采用全三维模拟，存在计算量巨大和所需内存量十分庞大的难题。相比于求解三维方程，求解针对轴对称流动的简化准二维Boltzmann模型方程，在计算量和内存量上少了一个维度，计算开销大大降低[1-2]，并且在轴对称特性得到满足的同时，也避免了繁琐的网格处理和全三维模拟网格生成过程中的奇异性问题[3]。因此相对于全三维模拟，发展一种基于准二维轴对称Boltzmann模型方程计算模拟的工程应用方法是十分必要的。

近几十年来，基于准二维方程来模拟轴对称流动的算法取得了飞速发展[2-15]。其中一部分算法[4-7]是基于准二维轴对称纳维-斯托克斯（Navier-Stokes,N-S）方程发展而来的。由于N-S方程是在连续性介质假设基础上建立的，其控制方程本身在稀薄流区与实际情况存在着至少是定量上的差距，因此该类算法无法完成全流域轴对称流动的模拟。另一部分算法[3,8-15]是基于Boltzmann方程发展而来。Boltzmann方程的建立基于如下两个重要假设[16]：（1）分子相互碰撞时只考虑二体碰撞，即认为3个分子或3个以上分子同时碰撞在一起的几率很小；（2）分子混沌假设。实践表明，不仅稀薄气体流动满足这些假设，而且处于海平面标准条件下的大气也满足Boltzmann条件，因此Boltzmann方程本身适用于全流域。为了模拟全流域轴对称流动，文献[17-21]通过研究确立描述各流域微观分子输运现象的Boltzmann模型方程，发展了气体分子运动论离散速度坐标法对速度分布函数进行数值离散，建立了可用于高、低不同马赫数宏观流动取矩的离散速度数值积分法。将计算流体力学有限差分无波动无自由参数（nonoscillatory nonfree dissipative, NND）格式[22]推广拓展到基于时间、位置空间和速度空间的Boltzmann模型方程数值求解，提出能可靠模拟从稀薄气体自由分子流到连续流的气体动理论统一算法[17-21]与大规模并行计算方法[23]，并开展了微机电系统（micro electro mechanical systems,MEMS）[19-20]、近地空间航天飞行器跨流域气体流动问题应用研究[24-25]，对本文进一步研究直接求解轴对称Boltzmann方程可计算建模提供了较强的研究基础与可行性。

目前，最常用的稀薄流计算方法是直接模拟蒙特卡洛（direct simulation Monte Carlo, DSMC）方法[8-11]。DSMC通过跟踪大量分子的自由运动和分子之间的相互碰撞，经过统计平均处理得到气体的宏观物理量，如密度、速度、能量、热流等，与直接求解Boltzmann方程是等价的[10]。由于DSMC方法本身涉及到统计平均过程，其中的统计误差造成了在低速流动中的统计涨落问题。另一方面，DSMC方法的物理空间网格步长受到分子平均自由程的限制，时间步长受到分子平均碰撞时间的限制[11]。当模拟连续流区的轴对称流动时，会存在计算效率低下、内存量十分庞大的问题，以致计算困难。因此基于DSMC模拟全流域轴对称流动的途径仍不是合适的选择。另一种方法是基于准二维Bhatnagar-Gross-Krook （BGK）类模型方程[3,12-15]。BGK类模型方程是基于Boltzmann方程的简化模型方程。研究发现，发展基于准二维BGK类模型方程的算法相比于基于笛卡尔坐标的算法来说，难度更大，其困难之处在于需要处理准二维模型方程中的轴对称源项[1]。轴对称源项来源于模型方程对流项的坐标变换，其中还包含速度空间的偏导。并且，离散求解轴对称源项对算法格式的精度、稳定性以及守恒性方面有很大影响[1]。

由于轴对称源项具有强非线性的特点，许多研究正在寻找简化轴对称源项的方法。Bergers[26]假设气体分子速度分布函数在轴向上处于平衡态，将非线性的轴对称源项简化为线性的，使得求解更加容易。He等[27]将轴对称源项中的气体分子速度分布函数基于Chapmann-Enskog （CE）进行展开，构造了低速轴对称流动的格子Boltzmann方法。Li等[28]基于CE展开，发展了求解连续流区轴对称流动的气体动理学格式（gas-kinetic scheme for Navier-Stokes equations,GKS-NS）。但是这些通过简化轴对称源项而构造出的算法，由于其特殊性，不能够适用于全流域模拟。只有基于原始的轴对称源项进行离散求解，才能对全流域轴对称流动进行模拟。根据这一思路，李诗一等[3]基于原始笛卡尔坐标下的时间演化解构造出了柱坐标下的轴对称源项的时间演化解，提出了基于有限体积法的全流域轴对称流动统一气体动理学格式（unified gas-kinetic scheme for axisymmetric flow,UGKS-AS）。

研究发现，若能适当修正BGK模型碰撞松弛参数和当地平衡态分布，经修正的BGK方程将能用于描述远离平衡态以至全流域复杂的气体流动问题[29]。基于Boltzmann方程可计算建模，李志辉等建立了一套全流域下的气体动理论统一算法[17-21,24-25]（gaskinetic unified algorithm, GKUA）。本文将基于气体动理论统一算法GKUA，采用新方法直接求解轴对称源项，并离散求解准二维Boltzmann模型方程，发展基于有限差分法的全流域轴对称流动气体动理论统一算法，并用于空天飞行环境喷管流动模拟[30-32]。

1 气体动理论统一算法Boltzmann模型方程

1.1 轴对称Boltzmann模型方程推导

将宏观流体力学与微观分子动力学连接起来的介观Boltzmann速度分布函数方程，可描述气体分子速度分布函数基于位置空间、速度空间任一时刻由非平衡态向平衡态的演化：

其中，f、f1和f′、f′1分别为两个分子碰撞前后的分子速度分布函数，V、V1为碰撞前的分子速度，g为气体分子相对运动速率，b为碰撞因子，ϵ为方位角。

气体动理论统一算法将该方程化为各流域不同尺度间分子输运现象统一模型方程，其在三维笛卡尔坐标系下的形式如下所示：

该方程通过描述气体流动过程中分子速度分布函数f对位置空间、速度空间和时间的变化率关系，基于气体分子碰撞松弛参数v和当地平衡态速度分布函数fN，将不同流域流态控制参数、宏观流动物理量、气体黏性输运特性、热力学效应及气体分子相互作用规则与分子模型用统一表达式联系起来，由非平衡态向平衡态的演化，将各个流域不同尺度间分子输运现象统一[17-21,24-25]。本文以此为基础，定义柱坐标系下的径向速度Vr和周向速度Vφ为：

经过坐标变换后，得到柱坐标系下的准二维Boltzmann模型方程为：

根据文献[1]，定义：

从而得到柱坐标系下的守恒型准二维Boltzmann模型方程为：

其中，

其中，x、r为柱坐标系下的空间位置，Vx、ζ、ω为分子速度，fM为麦克斯韦平衡态速度分布函数，p为气体压力，T为气体温度，Pr为普朗特数，n为气体分子数密度，q为热流，U、V、W为气体宏观流动速度，n∞为远前方未扰来流气体分子数密度，T∞为未扰来流温度，R为气体常数，χ为黏性系数的温度依赖幂指数，λ∞为未扰来流气体分子平均自由程。

1.2 轴对称源项数值离散

使用三角算子来离散轴对称源项：

该三角算子具有二阶精度，同时满足稳定性，可用于粗网格，也可基于显式Mac Cormack算子分裂思想，对轴对称源项进行前差预测、后差校正离散：

1.3 Boltzmann模型方程有限差分数值格式求解

采用守恒型离散速度坐标法消除气体分子速度分布函数对积分变量的连续依赖性，基于气体分子速度分布函数方程对流运动和碰撞松弛的非定常特性，采用非定常时间分裂数值方法，将离散后的模型方程分裂为代表碰撞松弛变化的非线性源项方程、位置空间对流运动方程以及轴对称源项方程，进行耦合迭代求解：

采用解析方法差分求解方程式（12），建立差分格式Ui+1=Ls(Δt)Ui，解除了数值格式稳定性条件下分子碰撞时间对时间步长的限制；将所得结果作为初值带入方程（13），采用NND-4（a）预测、校正两步格式求解方程（13），建立差分格式Ui+1=Lr(Δt)Ui；将所得结果作为初值代入方程（14），采用NND-4（a）预测、校正两步格式求解方程（14），建立差分格式Ui+1=Lx(Δt)Ui；将所得结果作为初值代入方程（15），采用二阶龙格库塔方法差分离散方程（15）的时间导数项，采用三角算子或者显式Mac Cormack算子分裂差分离散轴对称源项，进而求解方程（15），建立差分格式Ui+1=Lω(Δt)Ui。由此构造了求解轴对称Boltzmann模型方程的有限差分数值格式如下：

考虑到实际流动中气体分子速度分布函数方程的对流运动与碰撞松弛同时进行，为了避免差分离散引起计算顺序的差别，将公式（16）前、后时间步交替耦合计算，得到求解跨流域统一轴对称Boltzmann模型方程的有限差分格式为：

2 算法验证与分析

2.1 同轴圆筒间的定常旋转流动

考虑同轴圆筒间的气体流动，外筒保持静止，内筒旋转，流动仅与圆筒半径r相关，可模型化为一维轴对称模型。

图1给出了圆筒的示意图，外筒半径R2=2 ，内筒半径R1=1。内外筒壁面温度Tw=1，内筒旋转速度，无量纲气体常数R=0.5，气体平均密度为ρav=1，壁面采用漫反射边界，模拟气体为单原子气体。

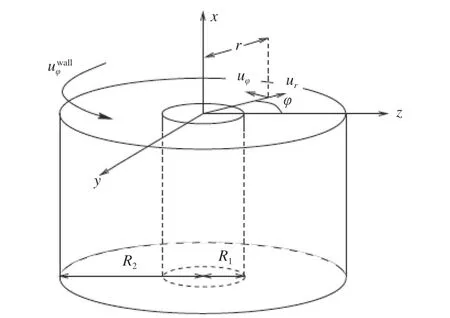
图1 圆筒间旋转流动示意图[1]Fig. 1 Schematic of rotational flow between two cylinders[1]

对于近连续过渡流0.02≤Kn≤10.0时，内筒旋转速度，气体动理论统一算法GKUA计算所得无量纲密度和速度与统一气体动理学格式（unified gas-kinetic scheme, UGKS）[3]结果对比如图2所示，可以看出二者计算结果吻合较好。

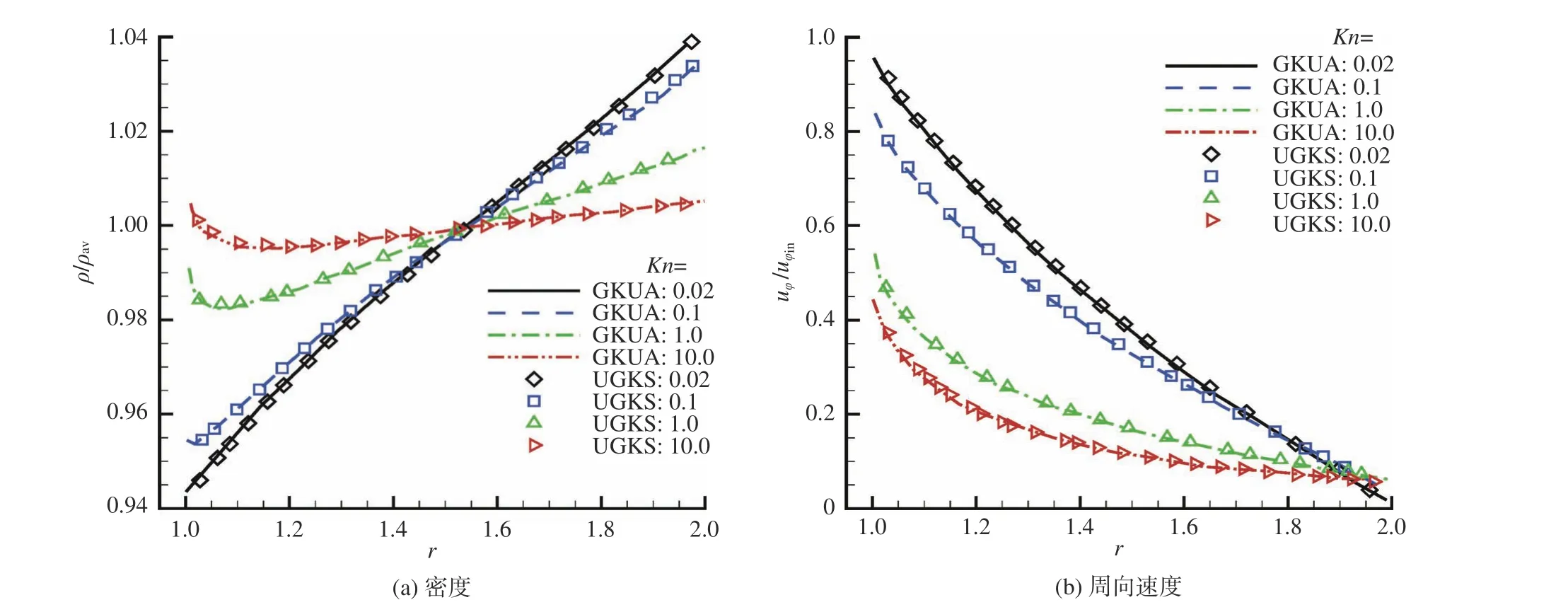
图2 同轴圆筒间定常旋转流动GKUA与UGKS方法结果比较Fig. 2 Comparison of results between GKUA and UGKS methods for steady rotational flow between two coaxial cylinders

图3给出了GKUA在连续流区和自由分子流区与其他方法计算的周向速度分布结果比较，其中当处于连续流区时，Kn=0.0001，uφin=0.1，处于自由分子流区时，Kn=100.0，uφin/=0.5。从图3中可以看出，在连续流区时，GKUA所得的周向速度分布与不可压的N-S解析解吻合较好；在自由分子流区时，GKUA所得结果与自由流解吻合较好。从图2、图3可以看出气体动理论统一算法GKUA可以准确可靠模拟全局克努森数0.0001≤Kn≤100各流域的轴对称旋转Couette流动。

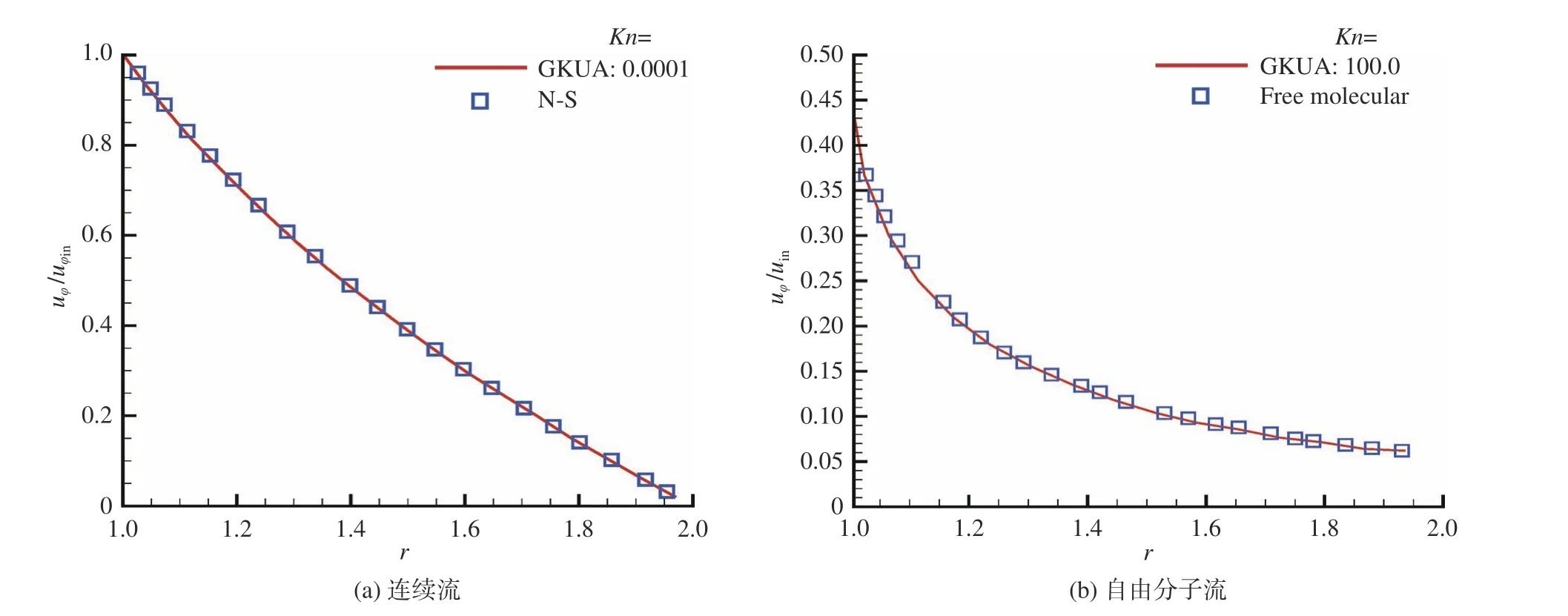
图3 同轴圆筒间定常旋转流动GKUA与N-S、自由流方法结果比较Fig. 3 Comparison of results between GKUA method and other methods for steady rotational flow between two coaxial cylinders

2.2 同轴圆筒间的非定常旋转流动

在同轴圆筒旋转速度突然改变的非定常旋转流动模拟中，内筒静止，外筒旋转。当t≤50时，外筒转速uφout/=1.0；当t＞50时，uφout/=-1.0。图4给出了Kn=0.02下不同时刻GKUA计算所得无量纲速度、温度、压力与DSMC结果[33]对比，二者吻合一致。

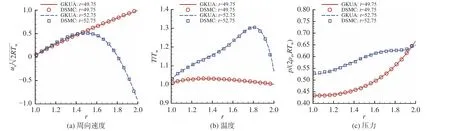
图4 同轴圆筒间非定常旋转流动GKUA与DSMC方法结果比较Fig. 4 Comparison of GKUA and DSMC methods for unsteady rotational flow between two coaxial cylinders

由于GKUA的求解过程是通过长时间的非定常模拟过渡到最终稳态，因此可以捕捉到同轴圆筒间气体流动的整个非定常演化过程，这也是区别于传统离散速度法 （discrete velocity method, DVM）或离散坐标法（discrete ordinate method, DOM）的独特优势。

2.3 轴对称喷管道内流动

选用型面如图5所示的喷管进行轴对称喷管内流动模拟。喷管喉道处直径5.1 mm，圆角半径1.3 mm，入口截面距喉道30 mm，出口截面距喉道50.7 mm，喉道前后壁面与轴线夹角分别为30°和20°。喷管入口压力pin=474Pa，温度Tw=300K，外部压力pout=1.529Pa，温度Tout=203.03K。

图5 轴对称喷管几何尺寸[34]Fig. 5 Geometrical size of the nozzle[34]

图6给出了轴对称喷管内流动物理量沿喷管轴线分布的GKUA和N-S方法结果的比较。横轴为轴线，取喉道截面处为坐标原点，从图中可以看出，两种方法计算结果变化趋势相符合，这也证实了本文GKUA方法应用于喷管内流动连续介质流动精细求解的正确性。

图6 轴对称喷管内流动物理量沿喷管轴线分布的GKUA和N-S方法结果比较Fig. 6 Comparison of the results of GKUA and N-S methods for the profiles of flow physical quantity in axisymmetric nozzle along the nozzle axis

图7给出了喷管轴线处GKUA方法计算的密度分布结果与Rothe[34]实验值的比较。横轴为距喉道的距离，Rt为喉道半径。从图中可看出模拟值与实验值符合较好。通过与实验数据进行对比，进一步确认了本文算法的可靠性。

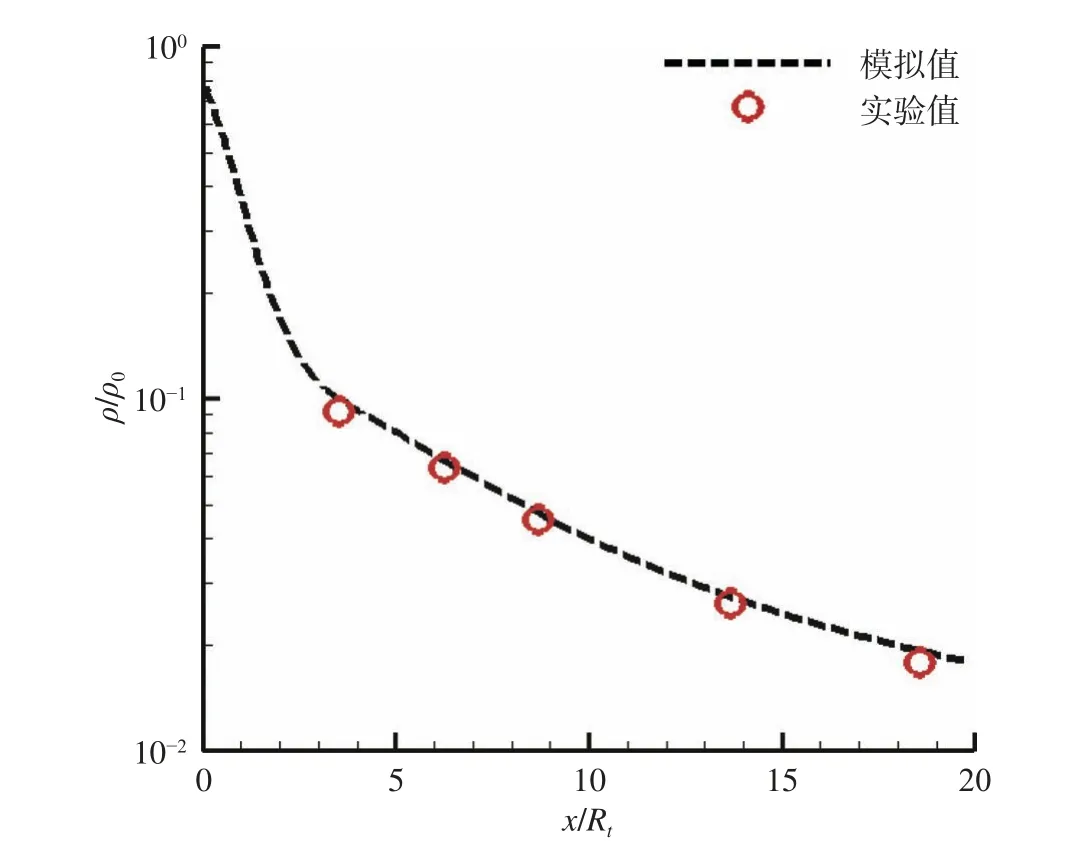
图7 喷管轴线密度分布模拟值与实验值比较Fig. 7 Comparison of the simulated and experimental values of the density profile of the nozzle axis

2.4 喷管核心区羽流环境算法验证与分析

为了准确分析空天飞行环境喷流/羽流特征，进行了低密度风洞羽流实验与轴对称Boltzmann模型方程统一算法及DSMC方法的验证结合。高真空机组提供扩压器实验段长时间稳定的真空环境，轴对称姿控发动机喷管中的气流在真空环境中急剧膨胀形成羽流。图8、图9分别给出了推力2 N发动机和推力10 N发动机羽流流场结构。发动机喷管根据姿控发动机的原型进行设计加工，其中2 N发动机喷管的收缩段和扩张段都是锥形型面，喉道直径为1.2 mm，出口直径为8.5 mm；10 N发动机喷管的扩张段型面是一圆弧，喉道直径为3 mm，出口直径为29.4 mm。图9（a）为辉光放电显示的流场，图9（b）为数值模拟得到的流场，可看出几种方法得到的流场结构一致。对于2 N发动机喷管，气流沿锥形型面膨胀，边界层厚度随着膨胀逐渐增加。由于10 N发动机喷管扩张段的型面为一段圆弧，对流动有一定的压缩作用，因而在喷管内形成一道激波。激波沿弧形壁面发展，与边界层相互干扰，形成一个复杂的波系结构，膨胀边界范围较大。比较分析图8、图9流动结构表明，推力2 N和10 N所形成的喷流/羽流流动状态有较大差别，2 N推力较小，所形成的羽流呈完全膨胀扩散羽流状；而10 N推力形成的喷管内流动在扩张段因边界层压缩，形成上下壁面附近两个压缩激波从喷管出口喷出，在离喷口一定位置相交衍生出两道膨胀波系，往后扩张形成马赫盘鱼尾状羽流往后膨胀扩散。

图8 推力2 N发动机羽流流场结构Fig. 8 Plume flow structure in the engine with 2 N thrust

图9 推力10 N发动机羽流流场结构Fig. 9 Plume flow structure in the engine with 10 N thrust

图10给出了推力10 N发动机羽流轴线上皮托管压力分布比较。模拟计算的气体介质为氮气，计算状态为：总压p0=8.0×105Pa，总温T0=773 K。从图中可以看出数值模拟结果与风洞实验结果比较接近，压力分布符合较好。

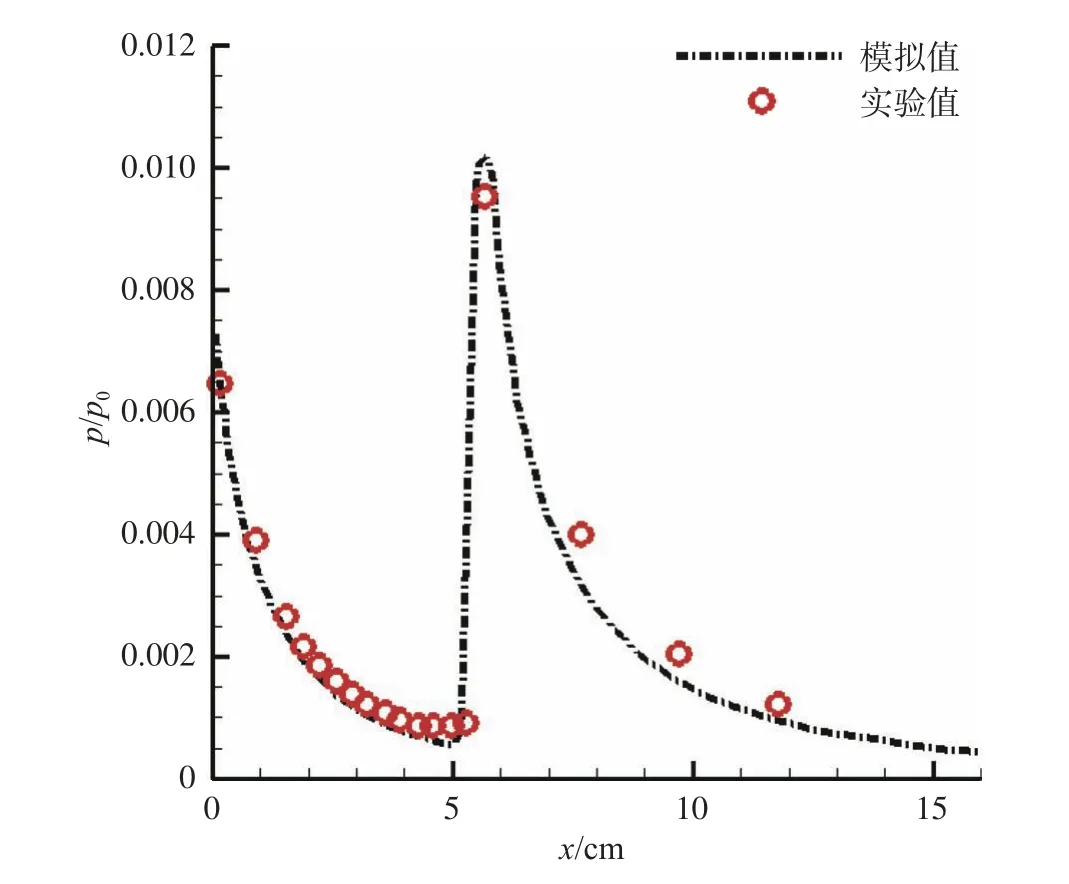
图10 在羽流中沿中心轴的皮托管压力比较Fig. 10 Comparison of the pitot pressure along the central axis in the plume

3 结论

通过数值模拟同轴圆筒间的定常/非定常旋转流动和轴对称喷管内流动，验证确认了本文轴对称Boltzmann模型方程统一算法处理全局克努森表征的全流域轴对称喷管流动的准确可靠性，同时相对于传统的离散速度坐标法，本文算法可靠捕捉轴对称流动的非定常演化过程。

通过与低密度风洞实验对比，计算得到的喷管出口核心区羽流结构一致、羽流轴线压力分布一致。对于在轨航天器，本文算法可用于一体化计算其发动机内部区域以及出口羽流轴对称核心区域，相比于全三维模拟，其计算效率将得到很大提高。未来将深入研究考虑内能激发多原子气体以及混合气体的轴对称模型算法，并将该算法与DSMC方法和低密度风洞羽流实验验证相结合，3种方法互为补充完善，预期可发展揭示空天飞行环境喷流/羽流流场演变机理与流动特征的数值与实验综合分析模拟平台。