双射流激波针在高超声速下的减阻降热特性

王俊峰，李 珺，罗世彬

(中南大学 航空航天技术研究院，长沙 410083)

0 引言

高超声速飞行器技术的发展是影响国家安全和社会进步的重要方面[1-2]。当飞行器以高超声速飞行时，会产生强烈的激波，激波后的压力和温度骤升将导致飞行器的气动力/热环境变得非常严峻。对于传统的被动式热防护系统而言，随着气动加热时间越长，所需热防护材料越厚，就会严重影响飞行器的有效载荷和航程。因此，为了高效降低高超声速飞行时的气动阻力和气动热，学者们提出了许多减阻降热新策略，主要包括激波针、逆向射流、能量沉积、迎风凹腔及其之间的组合。

其中，激波针以其结构简单且性能优异而被广泛关注。激波针的主要原理是将飞行器头部的强激波推离壁面，使其转变为斜激波，降低激波强度。此外，在逆压梯度的作用下，激波针在飞行器头部会形成回流区包裹壁面，从而降低壁面的压力和热流。关于激波针的研究始于20世纪50年代，并已成功应用于美国的三叉戟潜射弹道导弹，实现了52%的减阻效果，射程增加了近500 km[3]。然而，激波针也有缺陷：一方面，在高超声速飞行过程中，激波针替代了飞行器头部与来流直接接触，所以其头部温度很高，极易被烧蚀；另一方面，在一些工况下，带激波针的钝体肩部仍存在着激波/激波干扰，导致壁面热流和压力依然很高。因此，为了解决激波针头部的气动热问题、增强激波针的减阻降热效果，有学者提出了气动盘与激波针相结合的办法，文献[4-7]的研究证明了带气动盘的激波针的减阻降热性能明显优于无气动盘的激波针，而且能够对激波针头部形成很好的保护。

目前的研究主要是围绕激波针的长度、气动盘的尺寸和形状等方面来展开。范冰等[8]研究了激波针长度对钝体壁面的压力分布影响，发现随着激波针长度的增加，钝体壁面的压力和总阻力不断降低，但降低的速率逐渐减小。Sebastian等[9]指出当激波针的长度（L）超过钝体直径（D）的4倍时（即L/D大于4），其减阻降热性能不会进一步提高。Masoud和Hesam[5]以及黄伟等[4]比较了不同尺寸的气动盘的减阻降热效率，结果表明，随着气动盘尺寸的增大，钝体前的回流区逐渐扩大，钝体的阻力和热流逐渐减小；但是当气动盘的直径超过一定值后，气动盘反而成为产生阻力的主要部件，减阻效果有所降低。Srulijes等[10]在Ma= 4.5的来流条件下对比了平板式、球头式和尖锥式3种不同形状的气动盘的减阻效果，发现球头式和尖锥式气动盘的气动性能比平板式更好。何坤等[11]进一步比较了球形、半球形、尖锥形等6种激波针头部构型的流场结构和减阻降热效率，其中球形和半球形的减阻降热性能最好，其研究结果再次证明气动盘对于提高激波针的减阻降热有很大帮助。

除了使用气动盘外，在激波针前端使用逆向射流也能够同时满足保护激波针和改善减阻降热性能的要求。逆向射流通过喷孔将冷却介质注入流场中，射流在喷口处快速膨胀，将原本贴近激波针头部的激波推离。在膨胀过程中，射流速度逐渐增大，压强逐渐降低。射流的膨胀过程在马赫盘处终止 ，穿过马赫盘后，射流与来流相互作用形成交界面，并在来流的作用下偏转方向，与来流一起向下游流动。在下游处，由于逆压梯度的存在，会形成低温低压的回流区，回流区能够将壁面与高温气体隔离开，达到减阻降热的目的[12]。黄伟等[13]通过数值模拟方法研究了逆向射流激波针的减阻机理，并对不同射流总压比下的减阻效果进行了比较，发现随着射流总压比的增大，逆向射流激波针的减阻效果逐渐增强。屈峰等[14]则对逆向射流激波针的降热性能进行了分析，研究结果显示，在使用逆向射流激波针后，钝体壁面的热载荷降低率高达95%。为了获得最小阻力和喷流流量的最优解，张江等[15]结合实验、数值计算和响应面优化方法，研究了逆向喷流激波针的气动特性。除了传统的逆向射流激波针外，Gerdroodbary[16]和黄杰等[17-18]提出了一种新的逆向射流构型，将原本位于激波针头部的逆向射流转移到激波针根部，而在激波针头部使用气动盘对激波针进行保护。这种新构型能够直接产生回流区冷却壁面，因此拥有优异的减阻降热效率。随后，马坤等[19]对激波针根部逆向射流的方向进行了调整，使其与激波针的夹角为45°，以便于射流充分膨胀，提高逆向射流激波针的减阻降热性能。

遗憾的是，由于逆向射流激波针在攻角下存在强烈的激波干扰，所以减阻降热性能会严重恶化。何天琦和罗世彬[20]对攻角0°～6°范围内逆向射流激波针的减阻降热效率进行了探究，发现当攻角大于4°后，壁面的热流和压力已经超过基准钝体，逆向射流激波针已经不能再提供减阻降热效果。为了解决这一问题，许多学者提出了新的应对措施。耿云飞等[21]提出了自适应逆向射流激波针，能够使激波针随攻角的变化而转动，保证激波针始终正对着来流，降低了激波干扰的强度。姜宗林等[22]则提出了以激波针加侧向射流的组合构型来重构流场，以减小斜激波与再附激波之间的干扰，研究结果表明，即使在攻角4°的条件下，带侧向射流激波针的钝体壁面的压力降低率也可以达到65%。针对侧向射流激波针结构，朱亮等[23-25]分析了侧向射流在激波针上的位置对减阻降热性能的影响，发现侧向射流越靠近激波针头部，减阻降热效果越好；随后又对不同射流方向对减阻降热效率的影响进行了比较，发现逆向射流的减阻效果最好，侧向射流的降热性能最佳。李珺等[26]进一步将侧向射流、逆向射流和激波针结合，组成多射流激波针，该研究结果表明，与逆向射流激波针相比，多射流激波针在攻角6°条件下的阻力降低了36%，热流降低了53.8%。

综上所述，逆向射流激波针和多射流激波针均能大幅降低飞行器壁面的压力和热流，提升飞行器的气动性能。然而，逆向射流会产生额外的阻力，且随着射流总压比的增大，阻力迅速增加，并逐渐成为产生阻力的主要部件，从而影响激波针-射流复合构型的减阻降热效果。因此，针对这一问题，本文通过数值方法探究了一种新型双射流激波针复合构型的减阻降热特性。该构型包含后向射流和激波针根部逆向射流，能够利用后向射流的推力降低逆向射流附加阻力对减阻性能的影响，在满足热防护的要求上进一步提升减阻效果。此外，本文还对激波针的长度和射流总压比对该构型减阻降热性能的影响规律进行了分析。

1 物理模型和数值方法

1.1 物理模型

本文研究模型为轴对称球头模型，如图1所示。球的半径R= 25 mm，激波针的长度和直径分别为50 mm和4 mm，半球形的气动盘位于激波针头部，其半径Ra= 6 mm。在气动盘的背面和钝体的头部存在两个方向相反的射流，喷孔的面积均为5π mm2，其中位于气动盘背面的射流称为后向射流，后向射流的喷孔直径dr= 0.625 mm，射流的中心与气动盘肩部的距离为2 mm；位于钝体头部的射流称为根部逆向射流，逆向射流的直径dj= 1 mm。后向射流与逆向射流方向相反，能够降低逆向射流产生的阻力对结构总阻力的影响。双射流激波针的计算网格如图2所示。表1给出了本文研究的来流条件和射流条件，其中射流的介质为空气，壁面为无滑移等温壁面（Tw= 300 K）。Ma∞、p0∞、T0∞和Re∞分别为来流的马赫数、总压、总温和单位雷诺数，Maj和T0j分别为射流的马赫数和总温。PR为射流的总压比，其定义如下：

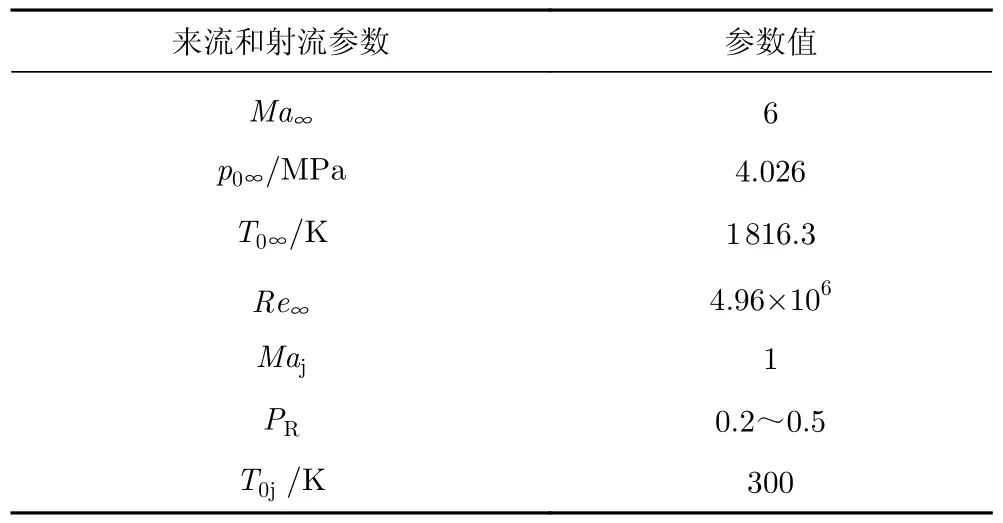
表1 来流和射流条件Table 1 Freestream and jet conditions

图1 双射流激波针示意图Fig. 1 Sketch of the dual-jet spike configuration

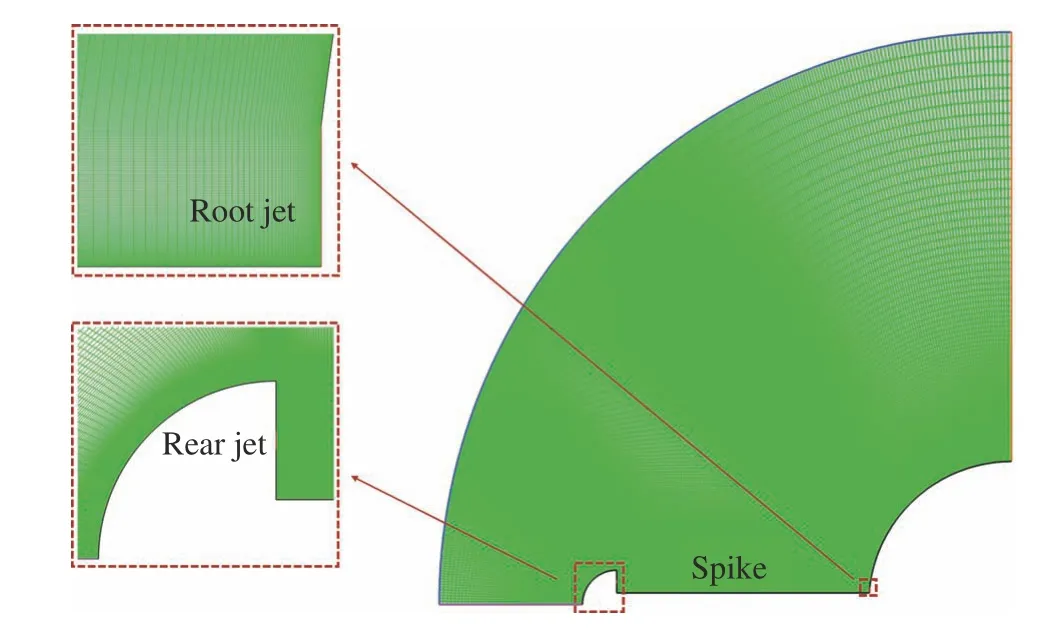
图2 计算网格示意图Fig. 2 Sketch of the computational grid

其中p0j为射流的总压。

1.2 数值方法

为了准确求解复杂流场，本文采用基于雷诺平均的二维可压缩Navier-Stokes方程（Reynolds-averaged Navier-Stokes equations, RANS）对双射流激波针的流场进行数值计算，采用SOU二阶迎风格式和AUSM空间离散格式来加快收敛速度，采用隐式LU-SGS格式对时间进行离散。考虑到流场中存在流动分离及再附等流动现象，选取SSTk-ω湍流模型对流场进行计算。控制方程详见文献[26]。

1.3 数值和网格无关性验证

在文献[26]中已选取Hayashi等[27]的喷流实验结果对本文数值方法进行了验证，相应的条件和对比结果可参考文献，此处不再赘述。

为了验证网格的无关性，本文以双射流激波针构型为研究对象，共选取了粗网格、中网格和细网格3种网格尺度进行计算，3种网格的选取如表2所示，其中ReΔx为网格雷诺数，计算公式如下：

表2 不同质量的网格Table 2 Different grid resolutions

其中，ρ∞、V∞和μ∞分别为来流的密度、速度和黏性，Δx为第一层网格高度。

图3为3种网格下计算得到的壁面压力和热流分布，图中θ为钝体上的点对应的圆心角。由图可知，3种网格计算得到的压力基本一致，而中网格和细网格计算得到的热流更为接近。同时，数值实验研究证明，当网格雷诺数接近或小于10时，则可以实现可靠的气动热预测[28]。因此为了节省计算资源，后续研究将采用中网格开展，保持ReΔx≈ 10。

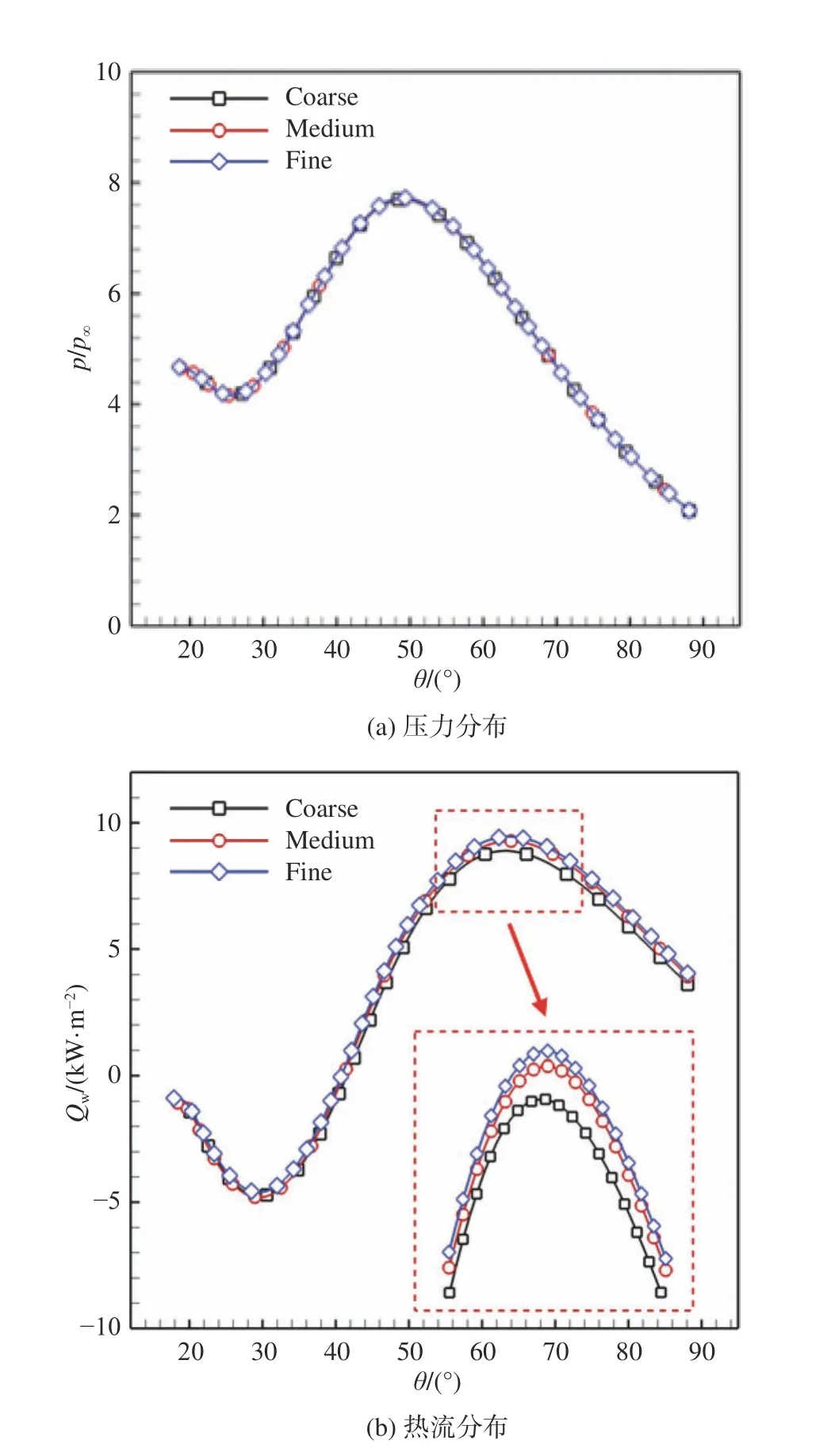
图3 不同网格下壁面压力和热流计算结果对比Fig. 3 Comparison of the wall pressure and heat flux for different grids

2 结果与分析

2.1 流场特性

为了探究双射流激波针的减阻降热机理及优势，本节对比了无射流方案、单一后向射流、单一逆向射流和双射流方案的减阻降热性能。激波针的长径比L/D= 1，逆向射流总压比PR,o和后向射流总压比PR,r为0.3，其余条件与表1保持一致。图4对比了4种减阻降热方案的流场结构，图中上半部分是马赫数等值线图和流线，下半部分是温度等值线图。对于无射流方案而言，如图4（a）所示，高超声速来流在半球形的气动盘前形成一道弓形激波，来流穿过激波后继续向下游移动，在气动盘的尾部发生分离，并在气动盘下游形成了一个小的回流区。在逆压梯度的作用下，钝体前形成了另一个较大的回流区。在回流区外，剪切层向下游发展，冲击钝体肩部，产生了再附激波。在无射流工况下，虽然气动盘与激波针组合后能够将原本贴近壁面的弓形激波推离壁面，降低壁面的压力和热流，但是从温度分布可以看出，气动盘与激波针组合构型的回流区温度依然很高。可见，无射流方案对壁面的热防护效果有限。当使用后向射流方案时，如图4（b）所示，后向射流在膨胀过程中形成了桶状激波、分离激波、射流边界等结构。在沿下游发展的过程中，后向射流受到激波针壁面的限制，射流结构整体向上倾斜，在沿激波针壁面流动一段距离后发生流动分离。与无射流方案相比，后向射流方案在钝体前形成的回流区的尺寸明显缩小，因此激波的再附位置向前移动。当采用逆向射流方案时，如图4（c）所示，气动盘附近的流场结构与无射流方案的相似，在气动盘的下游，由于逆向射流的引入，钝体前的大回流区被分成3个较小的回流区。与无射流工况和后向射流工况相比，逆向射流及其形成的回流区明显抬高了剪切层，使得剪切层冲击钝体的角度减小，引起再附激波强度的降低。而对于双射流激波针而言，如图4（d）所示，双射流激波针方案结合了后向射流与逆向射流的流场特征。

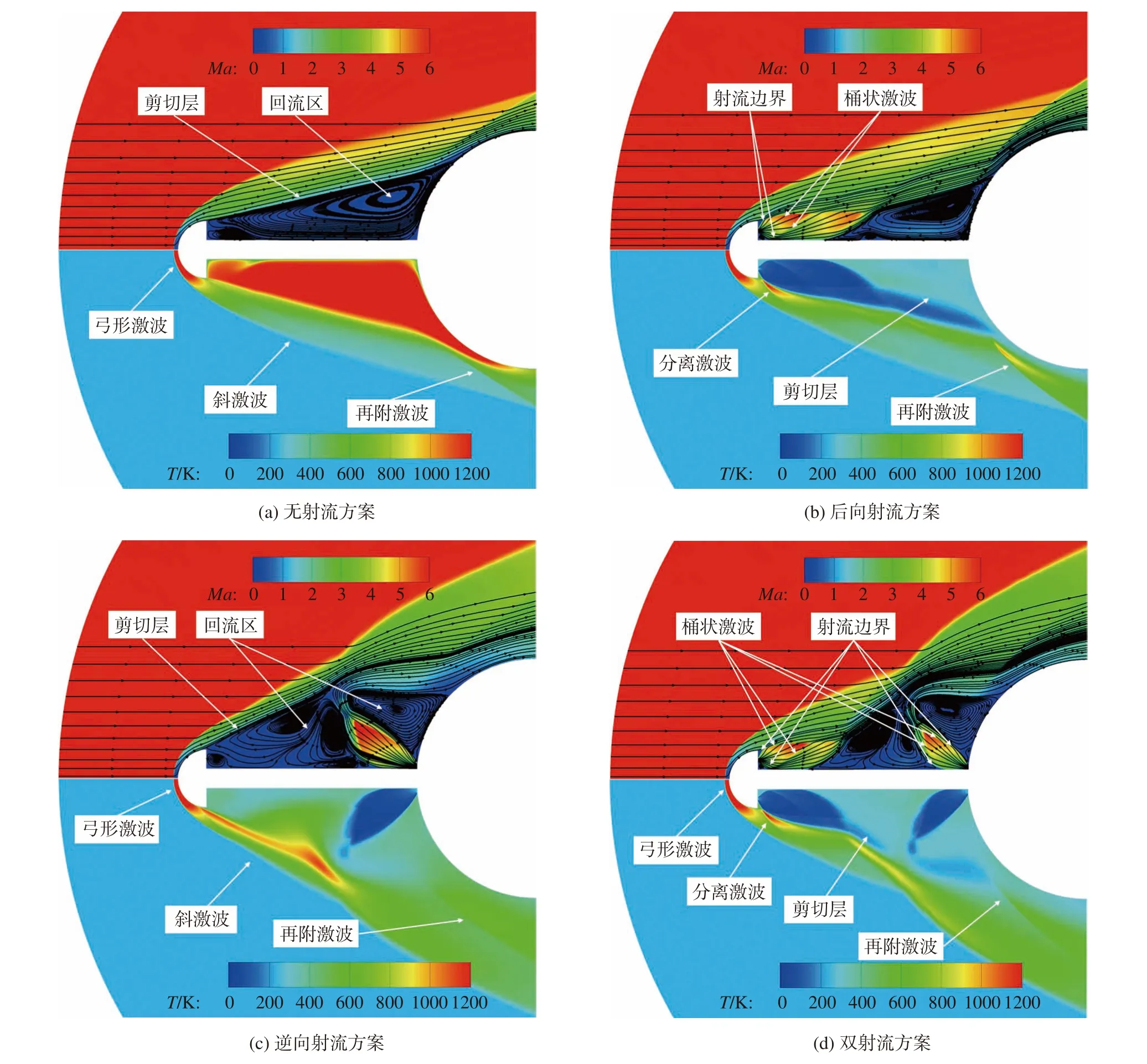
图4 不同方案的流场结构比较Fig. 4 Comparison of the flow fields for different configurations

一方面，与逆向射流方案相比，后向射流的加入使得逆向射流上游的回流区被压缩，导致再附激波的强度增大。另一方面，从温度分布图中可以看出，在双射流的作用下，大量的低温冷却介质被注入到流场中，所以钝体前的回流区温度较低，低温低压的回流区能够覆盖钝体的大部分，有利于降低钝体壁面的压力和热流。

不同减阻降热方式对应的壁面压力和热流分布如图5所示。由图可知，无论是压力还是热流，其变化的基本趋势都是先增大到一个峰值后再逐渐降低，这是因为在回流区中心处压力和温度最低。回流区沿着壁面向下游发展，气流逐渐被压缩，产生了一系列的压缩波，压力和温度逐渐增大，最终在再附点处，产生了再附激波，压力和温度达到峰值。随着气流继续向下游流动，由于流动通道的扩大，产生了膨胀波，压力和温度又逐渐减小。从图5（a）的壁面压力分布可知，当采用后向射流时，钝体前的回流区被压缩，导致再附激波强度增大，因此其壁面压力大于无射流方案。从上述流场分析可知，逆向射流的再附激波强度最低，因此其钝体的壁面压力最小。对于双射流激波针方案而言，由于受到后向射流的影响，其再附激波的强度大于逆向射流，因此双射流激波针的钝体压力略高于逆向射流方案。与无射流方案和后向射流方案相比，双射流激波针的壁面压力峰值分别降低了29.1%和42.6%。而与逆向射流方案相比，双射流激波针的钝体压力峰值则增大了32.9%。在壁面热流降低方面，由图5（b）可知（为了在同一图中方便清晰对比，无射流工况使用左边纵坐标，其他工况使用右边纵坐标），当射流加入后，流场的温度急剧降低，钝体的壁面热流也相应减小。在4种减阻降热方案中，双射流激波针的钝体壁面热流值最低。与无射流方案相比，双射流激波针的钝体热流峰值降低率达到了99%；而与后向射流方案和逆向射流方案相比，双射流激波针的钝体热流峰值分别降低了86%和89.8%。

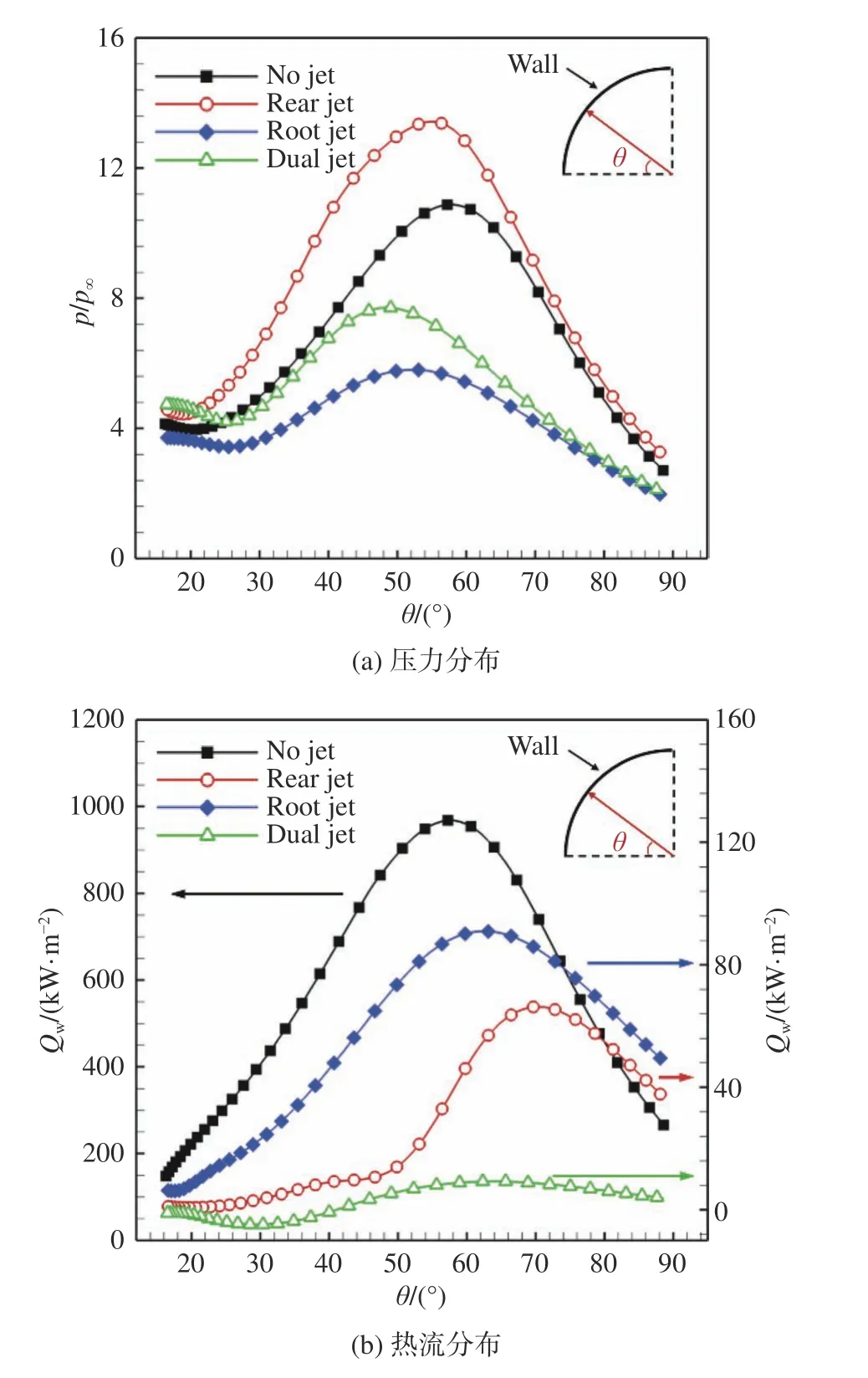
图5 不同减阻方式对应的壁面压力与热流分布Fig. 5 Wall pressure and heat flux distributions for different configurations

在4种减阻降热方案中，虽然双射流激波针的钝体压力略大于逆向射流方案，但是壁面压力的变化并不能代表最终的减阻效果，因此需要对不同方案的阻力系数进行定量对比。总阻力系数CD和钝体总热流Qt的计算公式如下：

式中，FD、Qw、Aref和D分别为各构型方案的总阻力、钝体壁面热流、参考面积（Aref= πD2/4）和钝体直径。

图6对比了4种减阻降热方案的总阻力系数和钝体总热流。由图6可知，虽然后向射流的钝体压力最高，但得益于后向射流的推力作用，其整体结构的总阻力系数却相对较低。与之相反的是逆向射流策略，虽然在逆向射流作用下，钝体的壁面压力最低，但是由于受到逆向射流附加阻力的影响，逆向射流方案的总阻力系数相对较大。相较之下，双射流激波针方案结合了后向射流和逆向射流的优势，且没有射流附加阻力的影响，因此其总阻力和钝体总热流最低。与无射流方案相比，双射流激波针工况下的总阻力和总热流分别降低26.7%和99.4%。在采用射流后，钝体壁面的热流均大幅降低，与后向射流方案和逆向射流方案相比，双射流激波针工况下的总阻力系数分别降低4.4%和40.5%，钝体壁面的总热流分别降低90.1%和96.3%。值得注意的是，从图5（b）可知，对于双射流激波针而言，在双射流的冷却效果下，钝体局部区域的热流会出现负值。

图6 不同方案的阻力系数和热流对比Fig. 6 Comparison of the drag coefficient and the total heat flux for different configurations

综上所述，双射流激波针综合了后向射流和逆向射流的优势，不仅能够将钝体附近的激波推离壁面，降低再附激波的强度，而且还能够产生更低温度的回流区包裹壁面，因此具有优异的减阻降热性能。

2.2 激波针长度的影响

随着激波针长度变化，双射流激波针的流场结构也会相应发生改变，从而影响双射流激波针的减阻降热效果。因此，为了分析激波针长度对双射流激波针减阻降热性能的影响，本节共选取了4种激波针长度（即L/D= 1、2、3、4）来进行研究。来流条件如表1所示，逆向射流和后向射流的总压比均保持为0.3，其余参数与2.1节保持一致。图7给出了不同激波针长度下双射流激波针的流场结构。由图7（a）可知，当L/D= 1时，由于激波针长度较短，后向射流与逆向射流之间的距离较小，因此由后向射流产生的下游回流区与逆向射流产生的上游回流区相互作用。值得注意的是，L/D= 1的逆向射流和后向射流均呈欠膨胀的“水滴状”，此时覆盖在钝体壁面的回流区尺寸较小。另外，由于激波针长度较短，钝体附近的斜激波与气动盘形成的弓形激波之间的夹角较小，激波干扰强度较大。当L/D= 2时，流场结构发生了显著变化：由于激波针长度增加，虽然后向射流沿下游膨胀的距离有所增大，但其产生的下游回流区与逆向射流产生的上游回流区不再相互挤压，因此逆向射流得以充分膨胀，由原来的欠膨胀“水滴状”转变为扇形区域，形成了马赫盘、三相点（马赫盘与桶状激波作用形成）等新的流场结构。由图7（b）可知，在马赫盘上游区域，逆向射流分为两部分：一部分向上游回流与后向射流掺混后向下游流动，并在压力梯度的作用下形成了一个新的回流区；另一部分则直接向下游流动，在钝体附近形成回流区，冷却壁面。与L/D= 1相比，L/D= 2的回流区更大，再附点位置更靠后，再附激波的强度更低。当L/D大于2时，如图7（c、d）所示，此时整体的流场结构与L/D= 2相似，只是局部略有变化。第一个变化是后向射流所形成的下游回流区：随着激波针长度从L/D= 2增加至L/D= 4 ，后向射流下游回流区逐渐缩小，到L/D= 4时，基本消失。第二个变化是马赫盘前的回流区和覆盖钝体的回流区尺寸：这两个回流区随激波针长度的增加逐渐增大，再附点位置逐渐向下游移动。从流场结构可以看出，当L/D大于2时，激波针长度的变化对再附激波强度的影响逐渐降低。

图8给出了不同激波针长度下双射流激波针钝体壁面的压力和热流分布，由图可知，激波针长度对钝体壁面的压力和热流具有非常重要的影响。根据上一段流场分析内容可知，随着激波针长度的增加，逆向射流下游的回流区扩大，再附激波的强度逐渐降低，再附点位置逐渐后移，因此，壁面压力不断降低，压力峰值点逐渐向下游移动，但是压力降低程度不断减小。从L/D= 1到L/D= 2，再附激波强度降低程度最大，壁面压力降低量最多，压力峰值降低58.2%。而从L/D= 2增加到L/D= 3，激波针长度的增加对再附激波的影响大幅降低，压力峰值降低率为26.6%。而L/D= 3和L/D= 4之间的壁面压力相差不大，两者的压力峰值只有约8%的差异。

图8 激波针长度对双射流激波针壁面压力和热流分布的影响Fig. 8 Influence of the spike length on the pressure and heat flux distributions of the dual-jet configuration

由图8（b）可知，随着激波针长度的增加，双射流激波针钝体壁面的热流变化趋势与压力相反。具体而言，从L/D= 1到L/D= 4，壁面热流逐渐增大，热流峰值逐渐后移，但热流的增长率逐渐降低。产生这一现象的原因如下：比较图7（a）和图7（b）可知，当L/D= 1时，一方面后向射流距离钝体壁面较近，能够有效地冷却壁面；另一方面，后向射流与逆向射流距离较近，两者形成的回流区相互作用能够使逆向射流的冷却介质全部向下游流动， 因此钝体附近的温度较低。而当L/D= 2时，激波针长度的增加使得喷流之间的距离增大、逆向射流的形态发生变化，导致大部分的逆向射流介质向上游回流，并与激波后的高温气流掺混后再向下游流动。因此L/D= 2的钝体附近的温度要高于L/D= 1，壁面热流也增大。比较图7（b）和图7（c）可以发现，这两种激波针长度下的流场结构几乎相同，但是随着激波针长度的增加，逆向射流向上游回流的距离逐渐增大，冷却介质与高温气流掺混的时间更长，所以钝体附近的温度有所增大，热流也相应增加。当L/D大于3后，逆向射流向上游回流的介质与高温气流掺混后的温度几乎达到稳定，因此继续增大激波针的长度不会使钝体附近的温度有明显提升，壁面热流的增长则相应降低。由图8（b）可知，从L/D= 1到L/D= 4，壁面热流峰值增加了7.5倍；而从L/D= 1到L/D= 2，热流增长幅度最大，热流峰值增大了约4.2倍。

图9对比了不同激波针长度下各部分结构产生的阻力和钝体总热流的变化。由图可知，随着激波针长度的增加，钝体所产生的阻力逐渐降低。当L/D小于3时，总阻力主要由钝体产生；当L/D= 3时，钝体和气动盘产生的阻力相近；当L/D大于3时，气动盘成为阻力产生的主要部件。从L/D= 1到L/D= 4，钝体阻力降低了83.8%，而气动盘产生的阻力几乎没有变化。对于总阻力的变化而言，由图9（b）可知，随着激波针长度的增加，总阻力系数不断降低，但是降低率逐渐减小；从L/D= 1到L/D= 4，总阻力系数降低了71.9%。而钝体总热流随激波针长度的变化趋势与总阻力系数相反，从L/D= 1到L/D= 4，钝体的总热流增大了13.7倍。

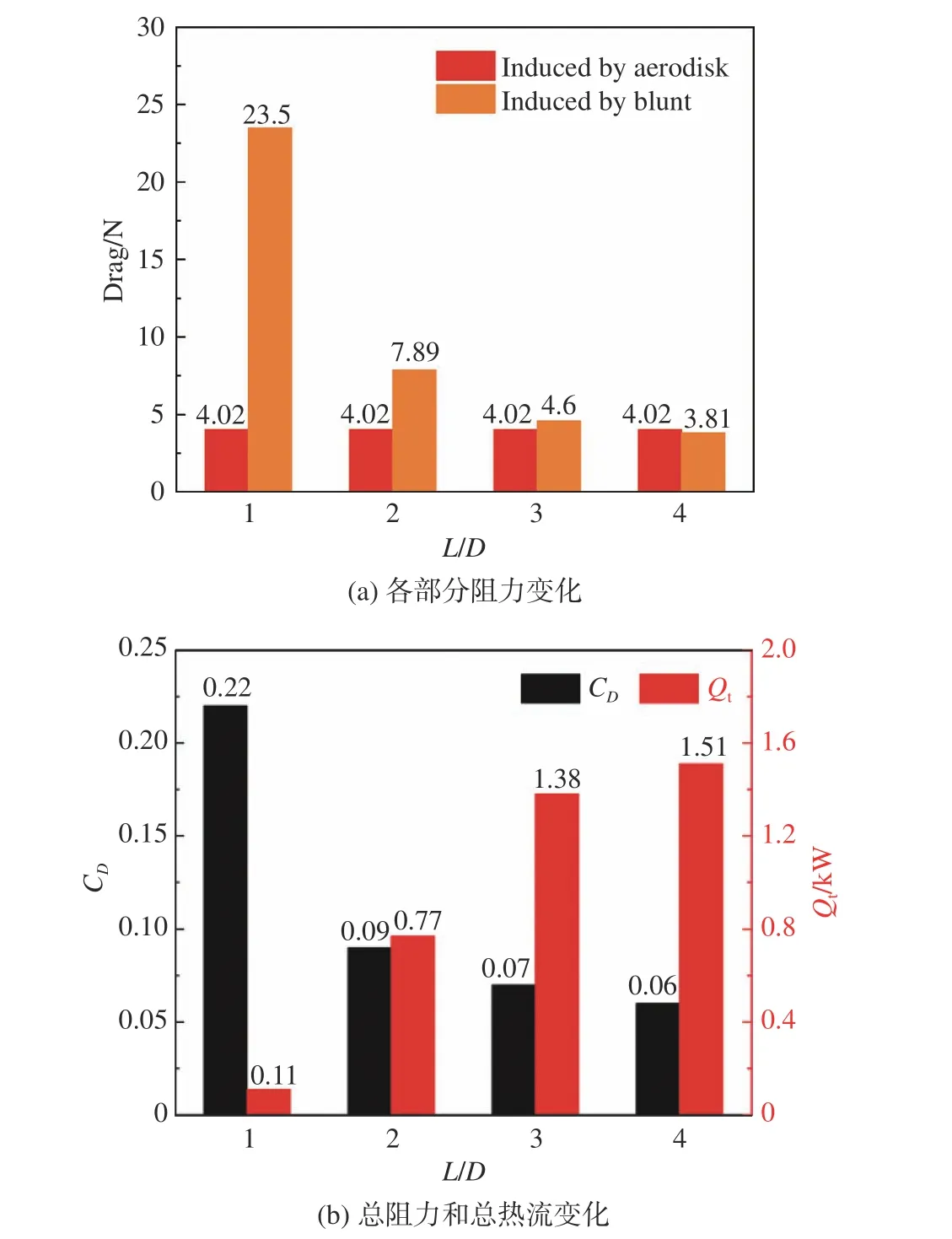
图9 激波针长度对阻力和总热流的影响Fig. 9 Influence of the spike length on the dragforce and total heat flux

2.3 射流总压比的影响

对于双射流激波针构型而言，除了激波针长度外，射流的总压比也同样对流场结构具有重要影响，因此，有必要研究射流总压比的变化对双射流激波针的流场及减阻降热效率的影响。本节共选取4种射流总压比（包括后向射流总压比和逆向射流总压比），分别为0.2、0.3、0.4和0.5。当研究逆向射流总压比PR,o对减阻降热性能的影响时，后向射流总压比PR,r= 0.3，其他条件与2.1节保持一致；当研究后向射流总压比对减阻降热性能的影响时，逆向射流总压比PR,o则保持为0.3，其他条件不变。

2.3.1 逆向射流总压比的影响

不同PR,o下的流场结构如图10所示，由图可知，随着射流总压比的增大，逆向射流的形态发生了明显改变：由PR,o= 0.2和0.3的欠膨胀结构变为PR,o=0.4和0.5的膨胀扇区，这一现象与激波针长度由L/D= 1变为L/D= 2时逆向射流的形态变化相似。随着射流总压比的增大，逆向射流的膨胀距离逐渐增大，膨胀区域也随之扩大。此外，从图10中可以观察到，无论逆向射流总压比如何变化，在L/D= 1时，逆向射流的冷却介质均没有向上游回流，而是全部向下游流动。因此，随着逆向射流总压比的增大，覆盖钝体壁面的回流区逐渐增大，再附激波的角度也逐渐增大，再附位置逐渐向下游移动。

图10 不同逆向射流总压比下的流场结构Fig. 10 Flow fields under different total pressure ratios of the opposing jet

图11为逆向射流总压比的变化对钝体壁面压力和热流分布的影响，可以看出，随着射流总压比的增大，壁面压力和热流均呈单调递减的变化趋势。对于压力变化而言，从图11（a）可知，随着PR,o由0.2增大到0.5，压力峰值降低24.1%。而对于热流变化而言，从图11（b）可知，PR,o从0.2增大到0.5，θ= 30°前的钝体壁面几乎均处于负热流状态，其热流绝对值从1.37 kW/m2增大到8.13 kW/m2；在θ= 30° 之后，随着PR,o的增大，壁面热流逐渐降低。当PR,o从0.2增加到0.5，壁面热流峰值降低95.8%；当PR,o大于0.4后，整体壁面的热流均为负值。

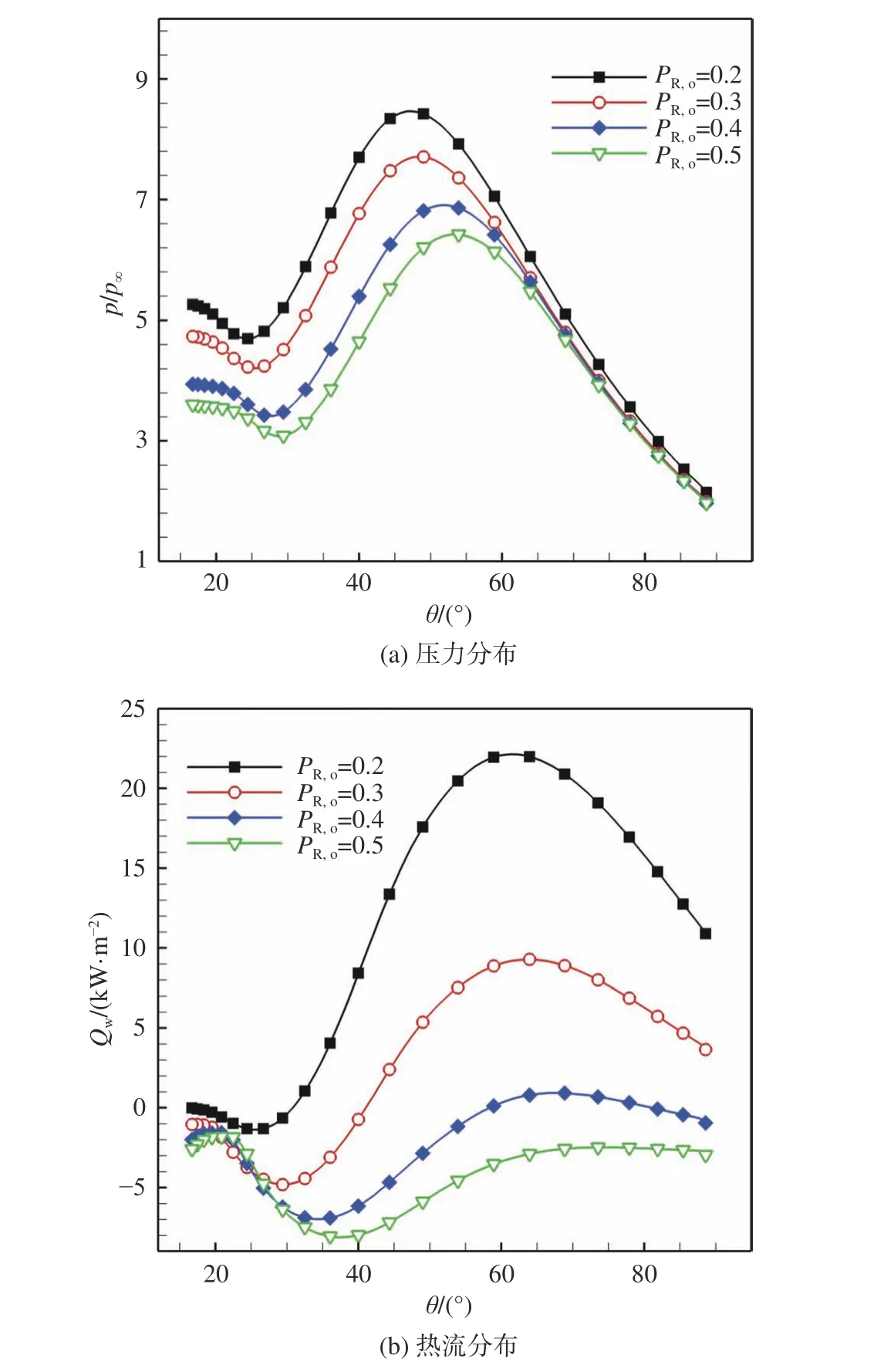
图11 不同逆向射流总压比下壁面压力和热流的分布Fig. 11 Wall pressure and heat flux distributions under different total pressure ratios of the opposing jet

随着逆向射流总压比的增加，钝体各部分的阻力及总阻力系数、总热流的变化如表3所示。表中，射流诱导的阻力Tj计算公式如下：

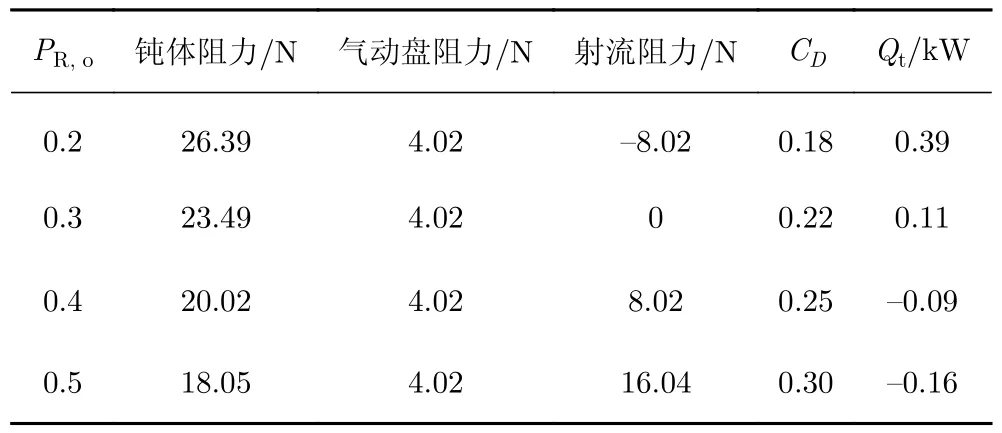
表3 不同逆向射流总压比下的阻力和热流Table 3 Comparison of the drag force and total heat flux for different total pressure ratios of the opposing jet

式中，m˙j、Vj、pj和Aj分别为射流的质量流量、速度、压力和喷孔面积。

由表3可知，一方面，钝体阻力与压力峰值变化趋势一致，均随着逆向射流总压比的增大逐渐降低，当PR,o从0.2增加到0.5时，钝体阻力降低了31.6%。另一方面，逆向射流总压比的变化对气动盘的流场结构并没有影响，在所有逆向射流总压比下，气动盘产生的阻力没有变化。然而，随着PR,o的增大，射流产生的阻力发生明显改变，并对总阻力的变化产生重大影响。当PR,o= 0.2时，后向射流产生的力大于逆向射流，因此会产生一个反方向的推力，降低整体阻力。当PR,o大于0.3后，逆向射流开始产生额外的阻力。因此，虽然钝体阻力随着逆向射流总压比的增大而降低，但是总阻力反而逐渐增大。当PR,o从 0.2增加到0.5时，总阻力系数增大了66.7%。与总阻力系数的变化趋势相反，增大逆向射流总压比后，钝体的热流逐渐降低，当PR,o大于0.3时，钝体的总热流均为负值。

2.3.2 后向射流总压比的影响

图12为不同后向射流总压比PR,r下双射流激波针流场结构的变化。由图可知，随着PR,r的增大，后向射流沿激波针壁面流动的时间更长，向下游发展的距离增大，产生的下游回流区减小。但是，由于逆向射流总压比保持不变，所以后向射流总压比的变化对逆向射流下游的流场结构影响不大。此外，从流场结构的对比可以看出，随着后向射流沿下游发展距离的增大，钝体附近的斜激波与弓形激波的干扰位置明显后移。

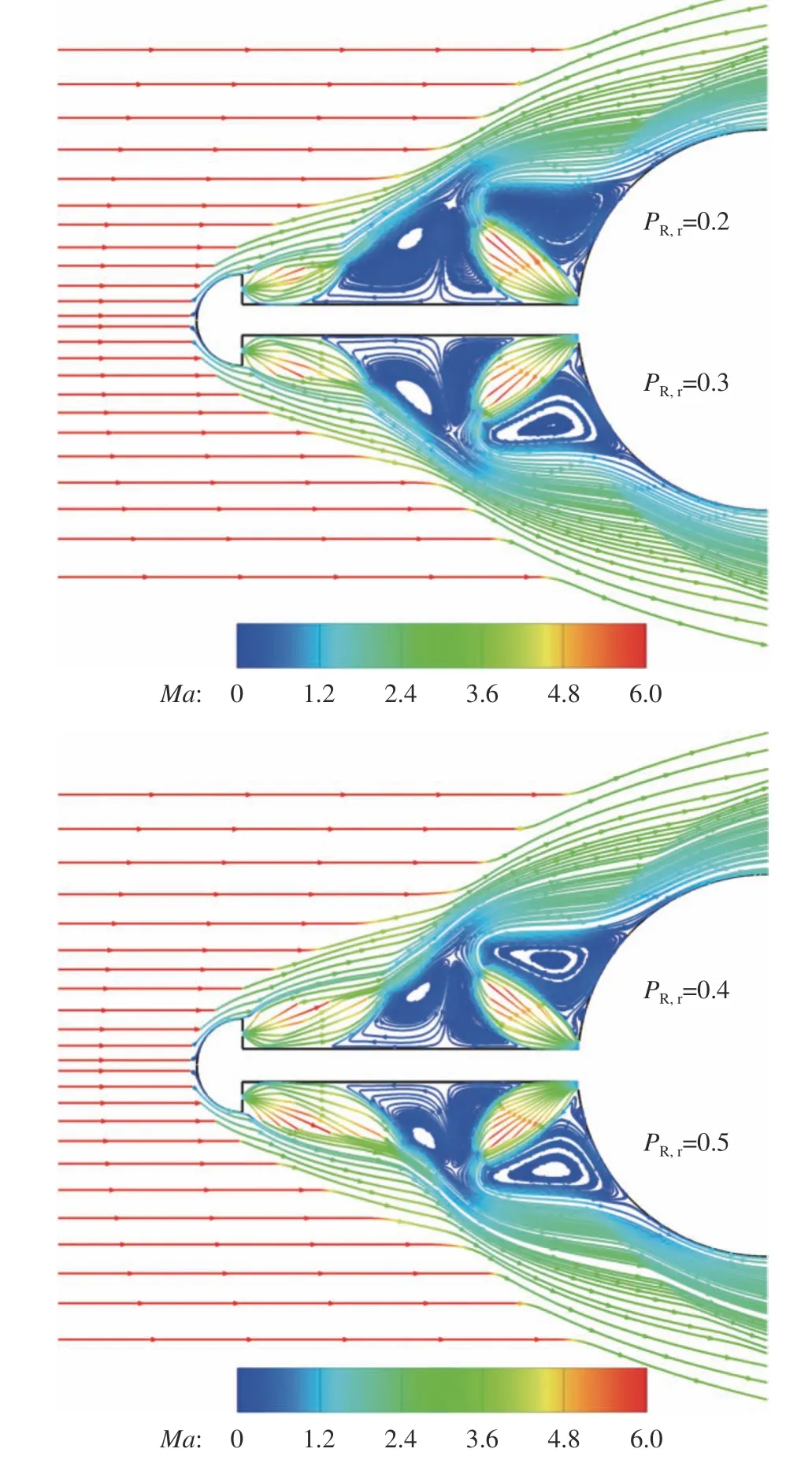
图12 不同后向射流总压比下的流场结构Fig. 12 Flow fields under different total pressure ratios of the rear jet

图13进一步比较了不同PR,r下钝体壁面的压力和热流分布情况，可以看出，随着PR,r的增大，钝体的压力逐渐增加。这是因为，一方面，逆向射流总压比保持不变，所以后向射流对再附激波的影响很小。另一方面，随着PR,r的增大，钝体附近的斜激波与后向射流附近的激波干扰位置逐渐后移，这就导致高PR,r工况下再附激波前的压力比低PR,r工况的更大，所以钝体壁面的压力有所升高。PR,r从 0.2增大到0.5，钝体壁面的压力峰值增大了26.6%。与压力相比，钝体热流随PR,r的变化趋势与压力正好相反。其原因主要有两个：其一，随着PR,r的增大，形成的结构欠膨胀程度更高，射流沿下游发展后能够达到的温度更低；其二，增大后向射流总压比相当于将更多的冷却介质注入流场中，激波后的高温流体在与其掺混后，温度增加程度更低。所以增大后向射流总压比可以显著提高双射流激波针的热防护性能。随着PR,r从0.2增大到0.4，热流峰值降低了73.8%；当PR,r大于0.4时，壁面热流均为负值。

图13 不同后向射流总压比下壁面压力和热流的分布Fig. 13 Wall pressure and heat flux distributions under different total pressure ratios of the rear jet

表4比较了不同PR,r下，各部分产生的阻力及钝体总热流的变化。从表中可以看出，随着PR,r的增大，钝体产生的阻力也随之增加，这一趋势与钝体壁面的压力分布随PR,r的变化趋势一致。然而，随着后向射流总压比的增大，后向射流产生的反作用力更大，并逐渐超过逆向射流产生的阻力，因此，总阻力系数随PR,r的增大而减小。PR,r从0.2增大到0.5，阻力系数降低59.3%。总热流变化与逆向射流总压比的情况相似，当PR,r大于0.3后，钝体总热流为负值。

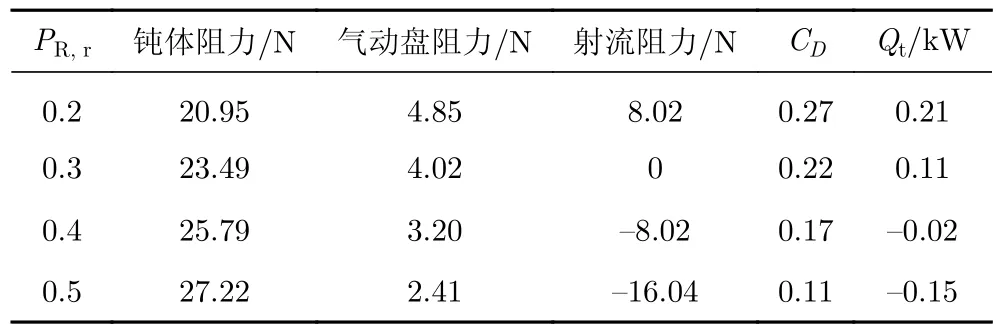
表4 不同后向射流总压比下的阻力和热流Table 4 Comparison of the drag force and total heat flux under different total pressure ratios of the rear jet

3 结论

本文采用数值模拟方法对后向射流和逆向射流激波针组合构型的流场结构和减阻降热效果进行了探究，并对影响该结构减阻降热性能的几个重要参数，如激波针长度、逆向射流和后向射流总压比，进行了详细分析，主要结论如下：

1）与非双射流的激波针方案相比，双射流激波针能够在不产生射流附加阻力的情况下降低再附激波的强度，同时向流场中注入冷却介质，形成温度更低的回流区包裹壁面，极大地降低了钝体产生的阻力和热流，对飞行器壁面形成更有效的保护。

2）增加激波针的长度能够显著改变双射流激波针的流场结构和减阻降热效果。随着激波针长度的增加，钝体阻力不断降低。然而，壁面热流的变化趋势与阻力恰好相反，从L/D= 1到L/D= 4，总阻力系数降低了71.9%，而钝体热流增加了13.7倍。

3） 改变射流的总压比同样可以使射流的形态发生变化。增大逆向射流的总压比PR,o，能够进一步降低再附激波的强度和钝体壁面的热流，但是对减阻不利；增大后向射流的总压比PR,r对再附激波强度的变化没有太大影响，但是得益于后向射流的推力作用，总阻力不断降低，而且随着PR,r的增大，有更多的冷却介质注入流场中，所以热流逐渐降低。

因此，在实际应用过程中需要综合考虑减阻和防热的需求，采用多目标设计优化，使减阻降热效果最佳。本文的研究结论可以为高超声速飞行器热防护系统设计提供一定参考，但是鉴于射流装置的复杂性以及实际操作过程中射流调节技术的局限性，双射流激波针用于高超声速减阻降热仍处于概念设计阶段，后续将与地面试验结合，使得研究工作的工程实用性更强。此外，由于在实际使用过程中，双射流激波针减阻降热是一个多场耦合问题，且激波针-射流的流场结构存在振荡现象，因此，未来将采用三维非定常方法对双射流激波针的流-热-固耦合机理以及流场振荡问题进行深入探究，为双射流激波针应用于工程实际提供更有指导意义的参考价值。另一方面，目前关于激波针-射流方案的应用对象基本都是钝化的飞行器头部，事实上，在飞行过程中，机翼前缘以及激波干扰处也存在极高的热流，因此后续也将把激波针-射流结构应用于飞行器的其他部分，以使这一减阻降热方案发挥更广泛的作用。