间断Galerkin有限元隐式算法GPU并行化研究

高缓钦，陈红全，*，贾雪松，徐圣冠，2

(1. 南京航空航天大学 航空学院，非定常空气动力学与流动控制工信部重点实验室，南京 210016；2. 南京工业大学 机械与动力工程学院，南京 211816)

0 引言

间断伽辽金（discontinuous Galerkin, DG）有限元方法源于求解中子输运方程[1]，在推广到求解非线性守恒方程（组）[2]之后才开始快速发展。前期流行的主要是显式龙格-库塔DG（Runge-Kutta DG, RKDG）方法[3]，后期人们追求隐式加速，著名的广义最小残差（generalized minimum residual, GMRES）DG[4]和下上对称高斯-赛德尔（lower-upper symmetric Gauss-Seidel, LU-SGS）DG[5]等算法开始涌现。DG有限元法融合了有限元与有限体积的优点，可在单元内基于选定的基函数直接拓展至高阶，具有所谓的任意高阶可构造性，适合利用其对工程中经常出现的激波干扰波系[6]和旋涡分离演变[7]等复杂流场细节进行高精度刻画；但该方法因高阶近似而涉及的未知量更多，同一网格上的控制方程求解消耗的计算量也就更大，这制约着DG方法走向实际工程应用[8]。因此，很有必要开展算法的并行化研究，尤其是围绕现代先进的图形处理器( graphics processing unit, GPU )硬件，尽可能地提高计算效率。

现代GPU大多拥有数以百计乃至千计的计算核，浮点运算能力强劲，适合并行处理数据密集且规模大的运算[9]。可以注意到，DG方法计算涉及的绝大多数操作都是在局部单元中进行，在单元中计算密集，所需模板（Stencil）也相对较为局部紧致，与GPU硬件特性匹配度高，十分适合GPU并行化[10]。GPU编程语言已从早期的低级语言发展到具有统一编程框架的高级语言，目前可供编程选择的主要有OpenCL[11]、OpenACC[12]和统一计算设备架构（compute unified device architecture, CUDA）[10,13]，其中CUDA最常用。Klöckner等运用CUDA统一编程模型结合求解三维Maxwell方程，开展了Nodal DG方法GPU并行化研究[14]。之后，Siebenborn等又发展了用于机翼等三维无黏绕流的数值模拟方法[13]。与之不同的是，Fuhry等则基于Modal DG方法实现了二维Euler方程的GPU并行化求解[10]，其线程结构是依据单元或单元边界构建的，适合非结构等任意网格，灵活性强，且这一非线性问题的并行化效率[10]与Nodal DG GPU算法求解线性问题[14]相当。Gao等[15]也依据此类线程结构研究了用于求解二维流动问题的RKDG GPU算法。

DG隐式算法GPU并行化的最大挑战是固有的数据关联依赖性[16]。这种依赖性会不可避免地因数据访存竞争引起线程冲突，进而导致计算出错。比较而言，为避免线程冲突，显式格式（RKDG等）GPU并行化改造相对容易，而隐式格式实现起来则困难得多。本文在显式RKDG GPU算法研究[15]的基础上，致力于实现隐式DG算法的GPU并行化。具体围绕求解Euler方程，用DG有限元法进行空间离散，采用经典的Roe格式处理数值通量，结合人工黏性方法[17]处理流场中可能存在的激波等间断问题，并选用常用的LU-SGS隐式格式进行时间推进求解。为了克服传统LU-SGS算法存在的数据关联依赖问题，发展了单元着色分组技术，用于计算域网格单元的着色分组，确保同一颜色的组内单元不再存在数据关联，进而使得LU-SGS算法时间推进能按颜色组别依次并行，形成DG LU-SGS并行化算法。在此基础上，为了把发展的算法移植到GPU上，先根据DG隐式算法的特点进行算法任务归类，再基于CUDA统一编程模型设计算法所需的核函数，并构建对应的线程与数据结构，发展形成LU-SGS DG GPU并行算法。最后，结合典型流动算例对发展的算法进行考核与性能测试，展示算法能基于隐式加速赢得进一步的GPU加速。

1 间断Galerkin有限元方法简述

这里结合DG方法求解三维无黏流动问题，给出GPU并行化涉及的空间离散与LU-SGS格式等相关问题。

1.1 流动控制方程

三维无黏流动问题的控制方程为Euler方程，在笛卡尔坐标系下可表示为：

式中：U=(ρ,ρu,ρv,ρw,e)T为守恒变量，F=(f,g,h)为无黏通量，

式中：u、v和w分别为x、y和z方向的速度分量；ρ和p分别为密度和压强，与单位体积总能e满足如下状态方程：

式中γ为流体的比热比，对于空气而言，γ=1.4。

1.2 空间离散

运用DG有限元方法，将计算域Ω∈Rd划分为Nc个互不重叠的单元Ωk的集合，定义如下有限元空间：

其中Uk是单元Ωk上的数值解。利用格林公式，对上式左端第二项进行分部积分，得到方程求解的空间离散弱形式[5]：

其中n是 单元边界∂Ωk上的外法向，dσ代表面元。可以看出，由于在DG方法中单元边界上允许存在间断，所以边界上无黏通量F的值是不唯一的。为此，常借鉴有限体积法中Riemann问题的处理方法，利用边界左右单元计算值U-和U+，构建数值唯一的通量函数H=H(U-,U+)，用以替换F[18]。H选用Roe格式[19]确定，那么式（6）可写为：

进一步，Uk用基函数ϕi(x)的线性组合[5]表示，即：

为处理流场中可能存在的激波等间断问题，抑制激波附近的非物理振荡，沿用文献[17]附加人工耗散修正项的做法，即把方程（1）改写为：

其中ε是人工黏性系数。结合BR2[20]格式处理梯度∇U，方程（10）可离散为：

其中单元上的人工黏性系数εk通过光顺指示器Sk计算确定。取守恒变量中的能量高阶项反映单元光顺度，定义，则

那么，εk可由下式计算确定[17]：

式中，sk=lgSk，s0=-4lgp，参数ε0=hk/p，κ为用户自定义常数；hk为单元尺度。可以看出，εk在光滑区趋于要求的0，即无影响；而在激波等非光滑区εk则随Sk增大而增大，起到抑制非物理振荡的作用。

需要注意的是，式（11）中与人工黏性相关的Ha沿用BR2格式[20]的处理方式，可表示为：

最后，经计算域单元汇总，得到：

式中：M是总体质量矩阵，该矩阵为块对角矩阵，每一矩阵块对应一个网格单元；为总体解系数向量；为总体残值向量。

1.3 时间离散

可选用显式或隐式对式（15）进行时间离散求解。相较于显式格式，隐式格式中推进时间步稳定性条件限制不严苛，步长大、收敛快，可赢得所谓的隐式加速。因此，人们追求基于隐式格式发展并行化算法，以求进一步加速[16,21]。

采用隐式时间离散，式（15）可改写为：

其中Λ为谱半径。为稳定计算，在初始ns迭代步采用指数增长形式的变CFL数。令CFLmin和CFLmax分别对应最小和最大的CFL数，并引入参数：

那么，第n时间步的CFL数为：

本文后续计算中，CFLmin、CFLmax和ns统一设置为1、100和2000。

其中Ci为单元i的关联单元（二维共边，三维共面）编号集。假设Ci中的元素可根据大于与小于单元本身编号i，进行LU自然分割，那么式（20）用LU-SGS算法[24]求解过程可分为前扫和后扫两步：

前扫步：

后扫步：

本文将基于上式构建基于GPU并行加速的隐式DG算法，为此必须先对算法进行并行化改造。

2 LU-SGS算法并行化改造

2.1 数据关联依赖问题

因此隐式算法的并行化改造一直是学者们所关注的。在结构网格上，人们利用网格结构化的特征进行单元分组，实现算法的并行化改造。如SOR算法，通过结构网格单元红（Red）黑（Black）自然分组，组内单元互不关联，形成所谓的Red-Black SOR并行算法[25]。但对于无结构化特征的非结构网格，此类做法不能直接运用。Malte等利用四色定理[26]，将二维非结构三角形网格分为组内单元互不关联的至多4个颜色组，实现了隐式LU-SGS算法的GPU并行。本文则依据LU-SGS DG算法关联单元数据依赖的特征，发展一种面向任意网格的单元着色分组技术，用于式（22）和式（23）的并行化改造。

2.2 单元着色分组与LU-SGS算法并行化改造

注意计算域Ω∈Rd已离散为互不重叠的网格单元：。为了克服LU-SGS算法的数据关联依赖问题，根据式（21）中的关联单元编号集Ci，构建辨识区分关联特征的着色数组color(:)，使得对于∀j∈Ci,color(i)≠color(j)，其中color(i)∈N+代表单元Ωi的颜色。这就是所谓的单元着色过程，图1给出了具体的实施方法，记为算法1。

图1 算法1：网格单元着色Fig. 1 Steps for grid cell coloning (Algorithm 1)

算法1中第1行为数组color(:)的初始化；第2行选定起始单元c0并着色。一旦c0选定，最终着色结果也唯一确定。选取物面边界相连的单元作为起始单元，符合物面扰动向流场传播的特征。测试表明，不同起始单元对计算的影响可忽略不计。为方便，本文算例起始单元均选为编号最小的物面单元。第3～6行是着色循环体，遍历着色所有Ci中的单元。在最后第8行，提取所用颜色数Ncolor供后续计算使用。

这里结合着色实例（见图2），直观展示所提单元着色分组技术。图2（a）为结构网格的着色结果，可以看出，对于二维结构网格，只需两种颜色即可，其效果相当于Red-Black分组技术[25]。图2（b）则给出了非结构网格的着色结果，其网格的非结构性要求使用更多的颜色。本例图中为4种颜色，分别以1～4标记。

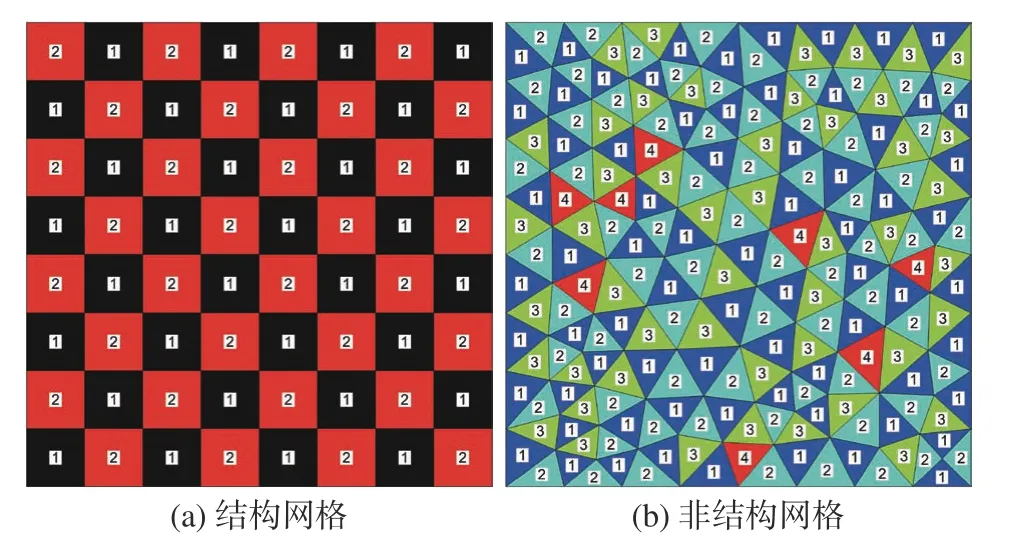
图2 二维网格着色示例Fig. 2 Examples of two-dimensional mesh coloring

在网格单元着色后，再按着色总数Ncolor构建如下颜色组：

由于组内单元已互不关联，可以按组别依次并行。图3列出了算法2基于单元着色分组的LUSGS并行过程。可以看出，并行化改造后的LUSGS算法关联单元编号集Ci是以颜色标记的大小进行LU分割，从第一个颜色到最后一个颜色完成算法的前扫步，后扫步则反过来，即从最后一个颜色循环到第一个颜色。需要注意的是，传统的LU-SGS算法（见式（22）和式（23））是依单元串行计算，改造后的算法是以颜色组群依次并行。下一节将进一步讨论该算法的GPU化，即最大程度地把算法移植到高性能的GPU架构上，赢得GPU并行化加速。

图3 算法2：LU-SGS算法并行过程Fig. 3 LU-SGS algorithm parallel preocess (Algorithm 2)

3 DG有限元GPU隐式并行算法

3.1 算法的整体框架

算法的GPU并行化就是算法从CPU到GPU的移植过程。为实现高效移植、赢得GPU加速，有必要兼顾算法特点与GPU硬件特征。目前，GPU硬件大多内嵌几百乃至数千的计算核，适合并行处理规模大且计算密集的运算，但在涉及逻辑判断和分支结构等计算时表现不佳[15]。为此，对算法2进行任务归类，并与CPU协同运行。如图4所示，前、后处理等相关部分保留在CPU上执行，时间推进迭代部分最耗时，因此移植到GPU上计算。一旦指派到GPU上的各项任务计算完成，再把计算结果传回CPU。可以看出，每一时间推进步由残值计算、全局系统矩阵计算、前扫和后扫等子任务构成，每一个子任务则对应一个GPU核函数（Kernel）。因此，从某种意义上，算法的GPU化就是对各类子任务创建对应的核函数。本文选用广泛使用的CUDA C编程语言构建核函数。必须指出的是，就LU-SGS DG隐式算法而言，全局系统矩阵更新、算法中的前扫步和后扫步运算等相关核函数是最为至关重要的，必须结合算法的特点和GPU访存等硬件特征来构建。

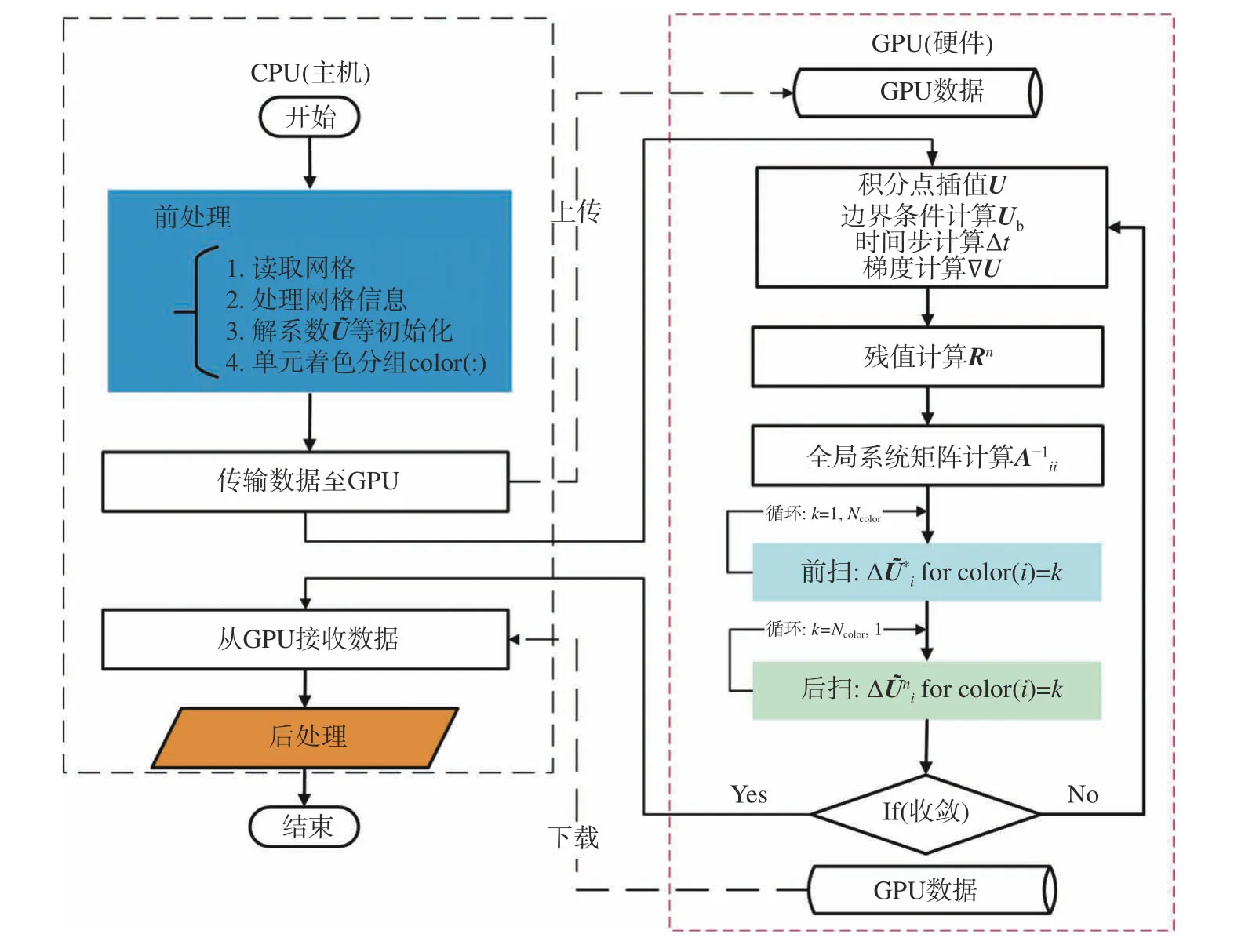
图4 LU-SGS DG算法GPU并行架构Fig. 4 General procedure of GPU-based LU-SGS DG algorithm

3.2 核函数构建问题

核函数的构建与GPU上各类存储器的利用和线程结构的创建密切相关。计算所需的线程（Thread）被集合为若干个线程块（Block），再由Block汇集成线程网格（Grid），形成所谓的Grid-Block-Thread线程结构。Block中的线程号（threadIdx.x）、Block号（blockIdx.x）以及自定义的Block维度（blockDim.x）等内置变量，用来计算确定Grid中的每个具体的线程编号[27]。依据上述创建的线程结构实现核函数的调用，其调用效率还与GPU上各类存储器（访存速度与存储空间大小不一）的合理利用相关。这些存储器按存储空间从大到小排列，主要有全局存储器、寄存器、共享存储器和常数存储器。容量最大的全局存储器适合存放计算产生的主要数据，但访存速度是所列存储器中最慢的，访存数据时要尽可能地利用对齐合并访问[27]，减少访存次数。访存速度最快的寄存器，数目相对有限，需要最大限度使用。共享存储器可用于线程块中线程间数据共享，但容量相对不大。具有缓存加速等特点的常数存储器容量十分有限，往往存放频繁使用且规模较小的常量。

如前所述，系统矩阵的迭代更新、前扫和后扫涉及的相关运算都是隐式DG算法所特有的，主要涉及单元和单元边界等积分计算（见式（11））。为了尽可能地满足对齐合并访问的要求，本文依单元设计创建积分运算核函数，并借鉴Fuhry等[10]的做法，依据单元构建相关核函数所需的线程结构，使得线程与单元相关的运算一一对应。依据这一原则，本文已对算法涉及的各子任务构建了对应的核函数。其中，最耗时的时间推进迭代相关的核函数已在图5中列出，并对代表性的核函数k_Diagvol和k_Fsweep给出具体说明。

图5 LU-SGS DG GPU算法时间推进调用过程Fig. 5 Time marching of LU-SGS DG GPU algorithm

核函数k_Diagvol用于计算单元积分对于全局系统矩阵中对角块Aii（见式（21））的贡献，其伪代码和必要的说明已在图6中列出。图中前两行计算确定线程号id并界定其范围；接着两行进行初始化；从第5行到第16行为核函数循环运算的主体，循环遍历所有单元积分点，并计算累加各积分点的贡献来更新对角块。

图6 核函数k_Diagvol的伪代码Fig. 6 Pseudocode of the kernel k_Diagvol

图7则给出了前扫核函数k_Fsweep 的伪代码和必要说明。该核函数用于完成算法前扫步运算，以颜色组群依次并行。图中前两行完成线程号id的计算与范围界定，涉及的Ns为颜色组Bs中的单元总数。接着为遍历单元所有边界的外循环（第4～17行），先根据关联单元颜色标记LU分割，确定需要计算的单元边界（第5行），再进入边界积分点内循环，遍历积分点计算累加更新残值；跳出外循环体后，计算更新解系数未知量（第20行）。

图7 核函数k_Fsweep的伪代码Fig. 7 Pseudocode of the kernel k_Fsweep

算法涉及的后扫核函数k_Bsweep也可以类似构建。至于残值、时间步计算等相关核函数，显式隐式类似，可参照作者先前有关显式GPU算法的工作[15]，这里不再一一赘述。不难发现，上述核函数的创建兼顾了数据结构构建与各类存储器利用，这些因素与GPU访存效率密切相关。

3.3 存储器利用与数据结构问题

如前所述，本文算法涉及的线程结构是利用了DG算法依单元计算密集的特征，依据单元或单元边界构建，线程运行相对独立，因此上述开发的核函数仅涉及全局存储器、常数存储器和寄存器。必须明确的是，为了提高核函数的并行效率，要尽可能地减少对慢速全局存储器的访存次数，最大限度地利用资源有限的快速寄存器。本文依据这一原则，常数存储器用于存放参考单元基函数相关的物理量，寄存器用于处理多次重复利用的数据（如k_Diagvol中的基函数梯度处理），而全局存储器则用于存放计算产生的大容量数据。但相比于CPU内存，全局存储器容量仍相对有限。因此，在设计核函数前，对运算所需数据进行了分析筛选，尤其是系统矩阵（见式（21））相关的大规模数据。本文只计算并存储了前扫和后扫中都需使用的对角块逆矩阵；将非对角块Aij相关计算嵌入前扫或后扫核函数（见图7），不再进行存储，以减少对慢速全局存储器的访存。

数据存放与调用涉及的数据结构，要尽可能地满足合并访问的优化要求[16]。这一点作者已结合RKDG GPU算法的工作进行了研究，发现将多维数组映射为连续的一维数组，使得具有相同物理特征的变量依单元或单元边界编号连续存放，有助于满足数据的合并访问，进而提高访存效率。本文发展的隐式算法沿用了这一做法，具体可参见文献[15]。

4 算例考核与性能测试

先选用二维单段/多段翼型和三维机翼等典型绕流，考核发展的LU-SGS DG GPU算法；再结合考核算例，进行GPU加速性能的测试与分析。

4.1 NACA 0012翼型跨声速绕流

NACA 0012翼型跨声速绕流算例常用来考核算法捕捉激波的能力[28]。本文对马赫数Ma=0.8和攻角α=1.25°的来流条件进行了数值模拟，计算得到的马赫数云图和物面压强系数分布见图8。从图8（a）的马赫数云图中看出，计算采用了较粗的混合网格，仅包含185个三角形单元和1706个四边形单元。图8（b）同时画出了二阶（p=1）到四阶（p=3）的计算结果，可从激波强度与位置注意到，由于网格较粗，二阶结果捕捉的激波横跨多个数据点，随着阶数的提高改善明显，表现为本文四阶结果与文献[29]更密网格（256×256）的四阶DG结果接近。这一点也可从表1的升阻力系数变化看出。

表1 NACA 0012翼型绕流的升阻力系数Table 1 Lift and drag coefficients of NACA 0012 airfoil

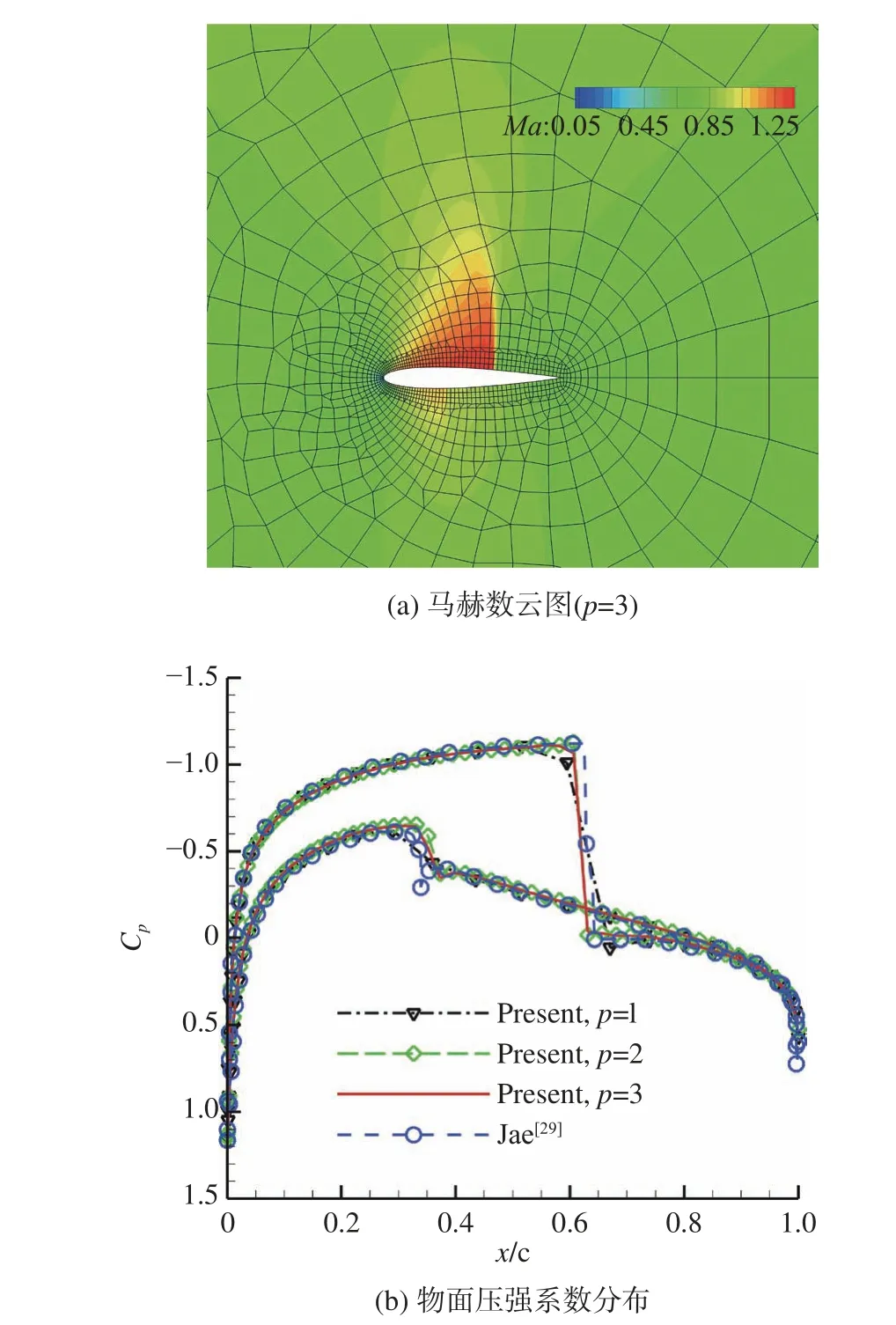
图8 绕NACA 0012翼型跨声速流动计算结果Fig. 8 Computational results of the flow over NACA 0012 airfoil

为了直观地展示加速效果，以四阶计算为例，图9同时给出了显式RKDG GPU算法和隐式LU-SGS DG GPU算法的收敛历程。如预期，发展的隐式算法比显式收敛速度更快（图9（a）），计算更省时（图9（b））。

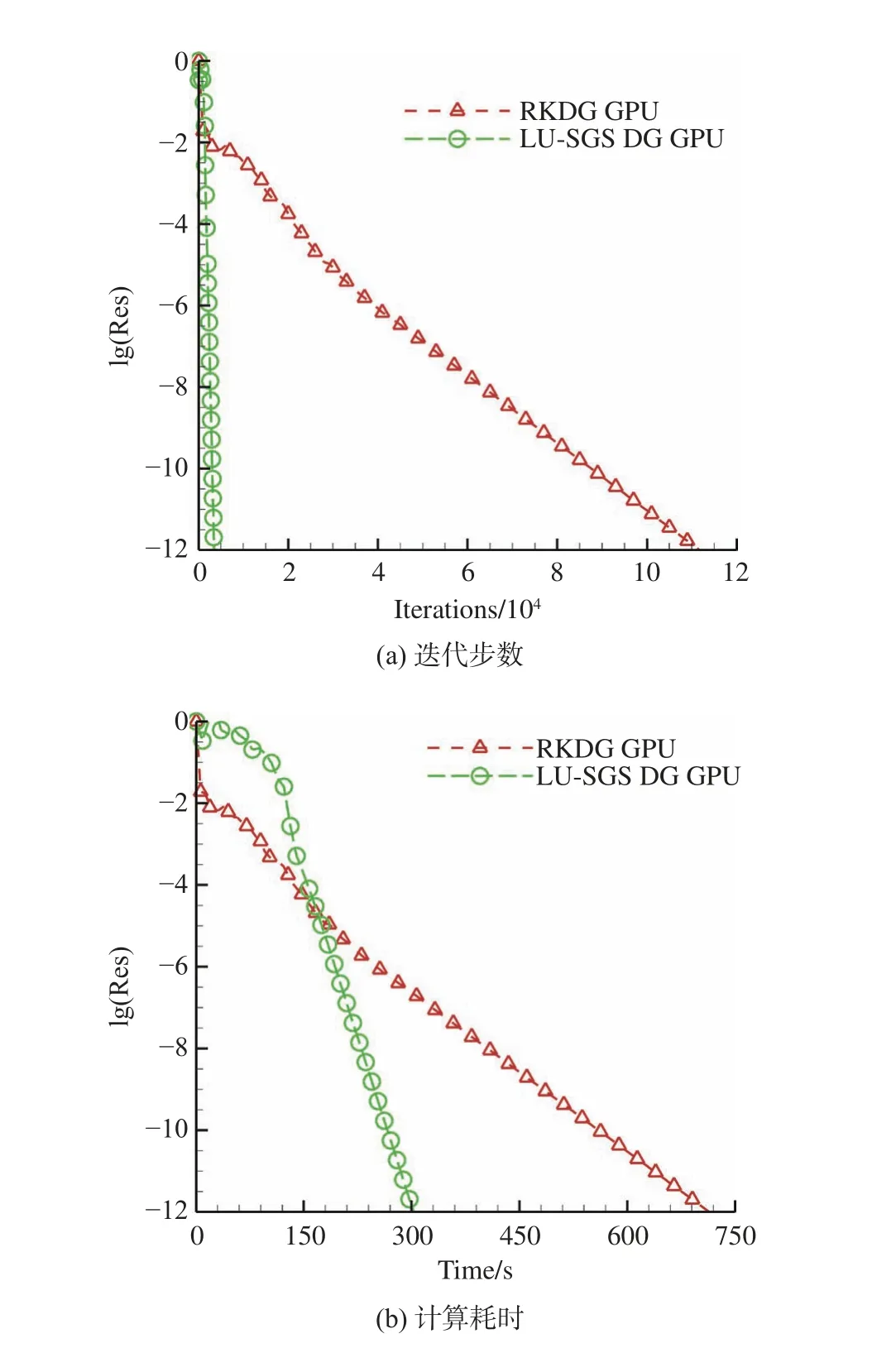
图9 NACA 0012翼型绕流的收敛历程Fig. 9 Convergence histories of flow over NACA 0012 airfoil

4.2 NLR 7301多段翼型绕流

为了展示发展的算法处理复杂气动外形的能力，本算例选用NLR 7301多段翼型亚声速无黏绕流，来流条件为马赫数0.185和攻角6°。计算网格见图10（a），圆形远场边界半径为30倍弦长，共包含5274个三角形单元，两段翼型表面网格点数相同，均取为65个点。在该网格上，采用发展的二阶（p= 1）到四阶（p=3）DG方法计算该绕流问题，计算得到的压力云图和表面压强系数分布已在图10中给出；图中同时给出了实验结果[30]和参考的SU2开源软件[31]密网格（包含51932个三角形单元）的无黏结果供比较。需要注意的是，SU2采用的密网格，其单元数已相当于DG所用网格的10倍。表2中则列出了对应的升阻力系数CL和CD。算例表明，相较于低阶SU2密网格结果，用四阶DG计算可获得精度相当的结果，且网格量可粗化到十分之一左右。

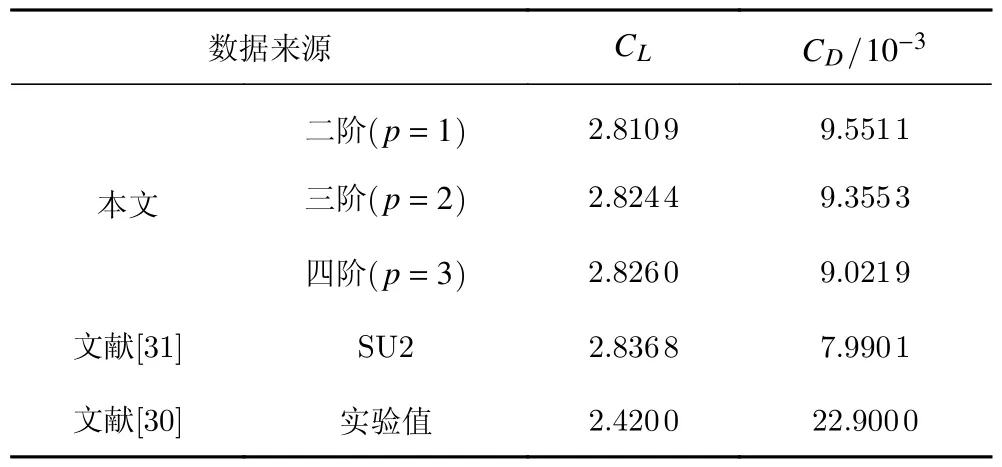
表2 NLR 7301翼型绕流的升阻力系数Table 2 Lift and drag coefficients of NLR 7301 airfoil

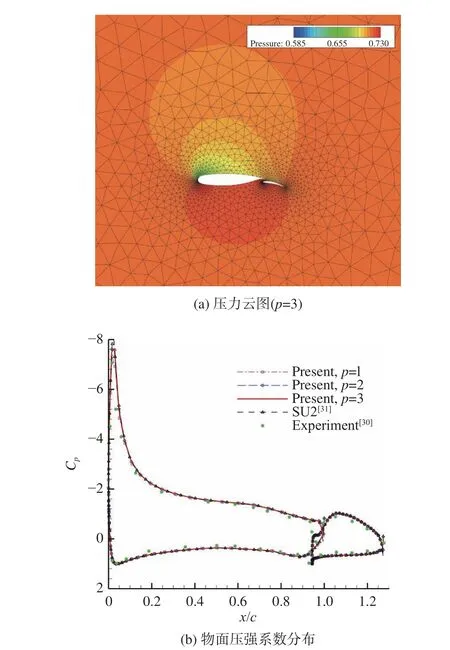
图10 NLR 7301翼型绕流的计算结果Fig. 10 Computational results of flows over NLR 7301 airfoil

4.3 M6机翼跨声速绕流

选用三维M6机翼实际外形绕流问题[32]考核算法的实用性。算例来流马赫数为0.84，攻角为3.06°。采用二阶（p= 1）和三阶（p= 2）DG算法，计算在仅有62897个四面体网格单元（相对稀疏）的网格上进行（见图11）。图12给出了三阶算法计算得到的物面压强系数云图和对称面压强系数等值线。不同算法计算的沿机翼展向非对称截面压强系数分布在图13中给出。从3个典型截面捕捉的激波位置和强度来看，随阶数提升，本文三阶结果总体上与实验结果[33]和文献[32]的无黏计算结果（四阶DG）较为吻合，展示出发展的算法模拟实际气动外形的能力。以三阶计算为例，三维算例再次证实，相较于显式GPU算法，发展的隐式GPU算法收敛速度的确更快（图14（a）），计算更省时（图14（b））。因三维算例的规模相对较大，这种特性更为显著，本算例消耗的时间仅为对应显式算法的十三分之一。

图11 M6机翼计算网格Fig. 11 Computational mesh of M6 wing

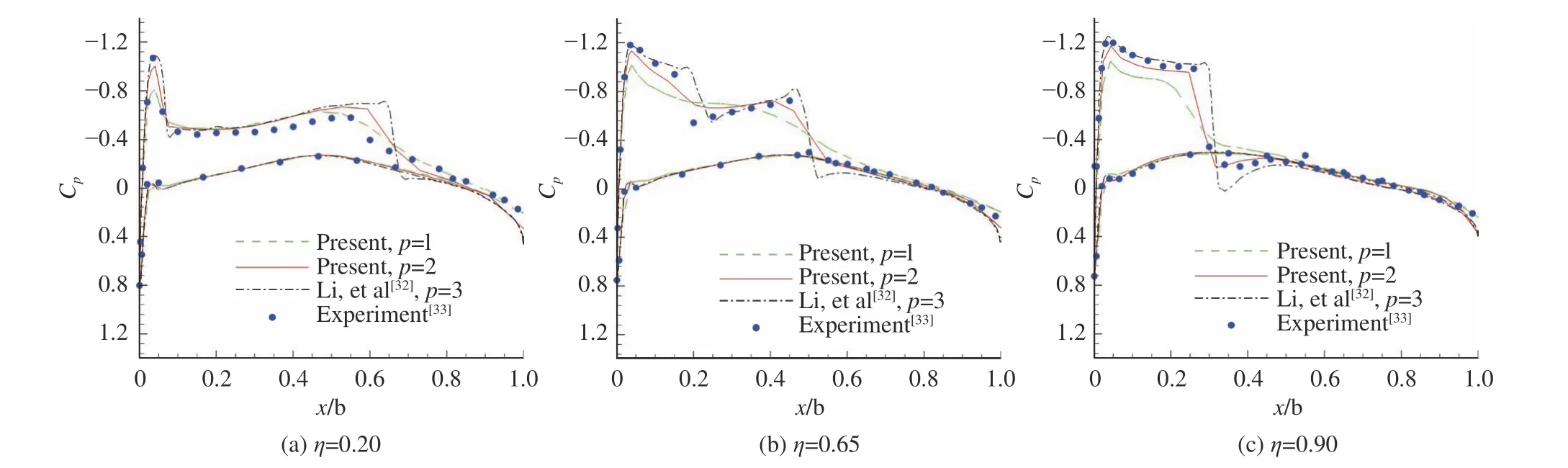
图13 M6机翼典型展向截面压强系数分布Fig. 13 Surface pressure coefficients at typical spanwise sections of M6 wing

图14 M6机翼绕流的收敛历程Fig. 14 Convergence histories of flow over M6 wing

4.4 GPU加速特性测试

如上所述，发展的隐式LU-SGS DG GPU算法是由CPU上的隐式LU-SGS DG算法移植到GPU上所得。为定量分析算法的GPU加速性能，设T为算法单一步时间步的计算耗时，并用下标区分算法在CPU和GPU上的耗时，那么隐式GPU加速比可定义为TCPU/TGPU。依照传统做法，T统一取为1000个时间步迭代耗时的平均值[9]。所有测试算例均以双精度运行在Windows工作平台上。该平台配备有英特尔i5-3450 CPU和英伟达GTX TITAN GPU等硬件，硬件性能参数可参见文献[15]。

4.4.1 规模效应

研究表明，GPU加速比与构建的线程块Block大小密切相关[34]。作者对显式RKDG GPU算法的测试也表明，Block中线程数取为64或128时，加速效果最好[15]。本文以64或128作为基准，考察了Block中更小或更大的线程数，按从小到大排列，线程数为8、16、32、64、128、256、512或1024。具体测试工作结合二维NACA 0012翼型和三维M6机翼绕流算例进行。同时必须注意，算例网格单元数应远大于GPU计算核数，即排除所谓的规模影响[34]，确保测试可信。为此，本文将网格相对较粗的二维算例加密至包含48639个三角形单元，三维算例网格规模已足够，保持不变。图15给出了对应的测试结果，图中横坐标代表线程块中的线程数，纵坐标为计算耗时。二维和三维不同阶数的测试结果都表明，当每个Block包含64或128个线程时，计算耗时最小。这一结果与文献[15]显式算法得到的结论一致。

图15 线程块大小对计算耗时的影响Fig. 15 Effects of the thread block size on computational time TGPU

为了不失一般性，设置Block中的线程数为64，测试网格规模对加速比的影响。图16给出了加速比随网格规模变化的曲线。可以看出，大体上，在达到GPU性能极限前，加速比均随网格规模增大而增大，最大可达18.64。

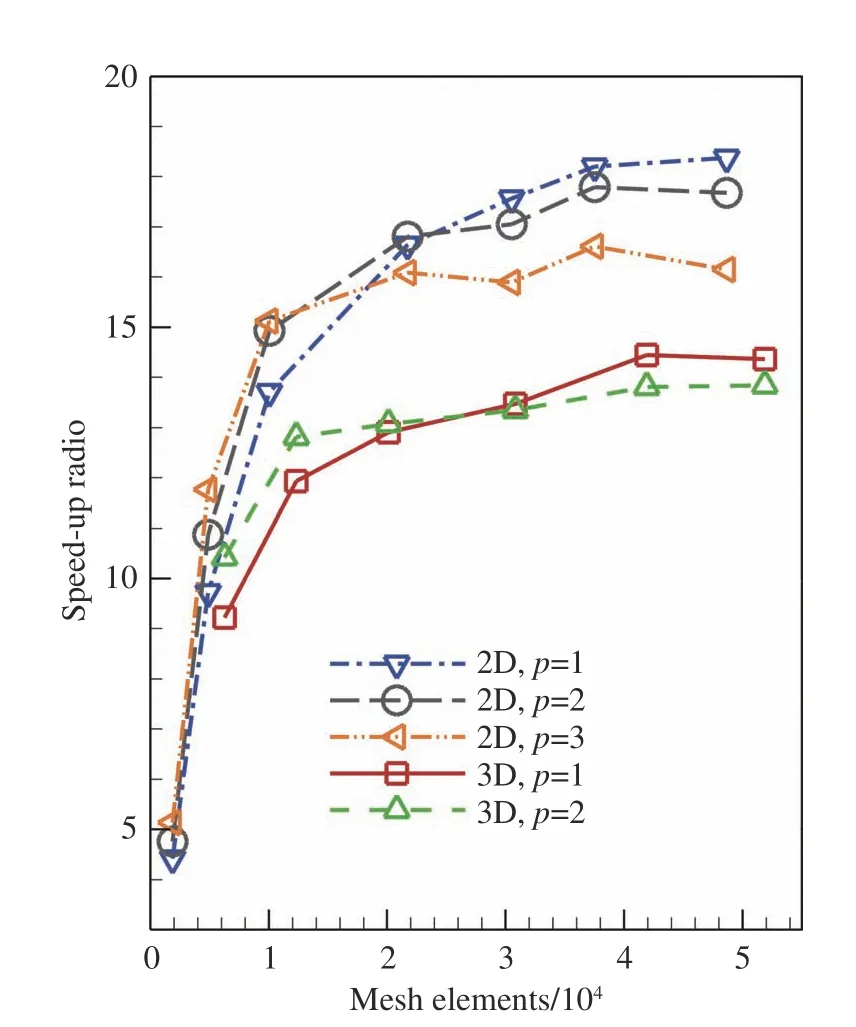
图16 网格规模对加速比的影响Fig. 16 Speedups with respect to different mesh sizes

4.4.2 隐式GPU算法总体加速性能

汇总4.1～4.3节中的算例，可以得到发展算法的总体加速性能。相关数据已在表3中列出。可以发现，不同阶数的算例测试都能赢得预期的GPU加速，二维算例加速比最高可达11.68，三维算例加速比则高达14.15。需要说明的是，此加速比是在隐式加速的基础上得到的，此外，规模较大的三维机翼算例能赢得更大的加速比，展示出算法处理此类大规模问题的潜力。

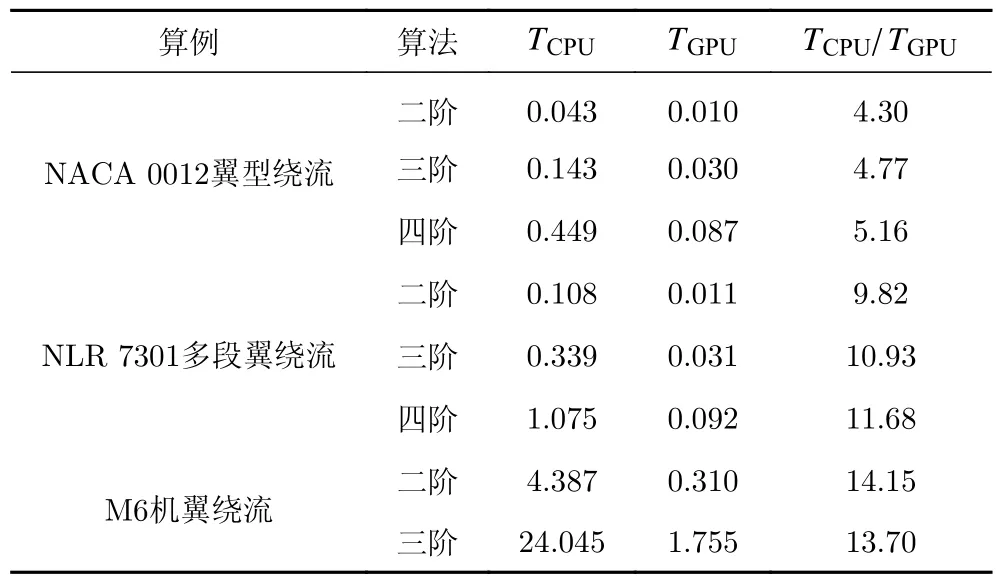
表3 隐式GPU算法的总体加速性能Table 3 GPU speedups of the developed algorithm

5 结论

本文遵循结构网格红黑着色分组思想，依据LUSGS DG算法关联单元数据依赖的特征，发展形成了一种面向任意网格的单元着色分组技术，并成功地用于隐式算法的并行化改造；在此基础上，基于CUDA统一编程模型，依据单元或单元边界创建了核函数与对应的线程结构，成功地把并行化改造后的算法移植到了GPU，形成了隐式LU-SGS DG GPU算法。发展的算法通过算例验证与性能测试，得到的结论主要有：

1） 所提单元着色分组方法可用于结构与非结构混合等任意网格，当用于结构网格时，该方法与传统的红黑着色法等价，因此可为其他隐式算法并行化改造提供借鉴。

2） 并行化LU-SGS DG算法是以颜色组群依次并行的，所需颜色数越少，并行化程度越高，因此，可用的任意网格应尽可能地选择结构化程度高的，以减少颜色数。

3） 发展的算法都能在隐式加速的基础上赢得进一步的GPU加速，较显式GPU算法更省时，且对三维等规模大的数值模拟加速效果会更好。

4） 算法是依单元面向任意网格构建的，可以灵活地处理涉及复杂计算域的离散问题。

当前算法中线程结构主要是依据单元构建的，下一步可结合DG算法的特征，考虑不同的线程结构，进一步完善本文发展的算法。