基于AD与TRIZ的加工中心主轴松拉刀机构优化设计

2024-03-14左斌王仁忠陶宇王敏

机床与液压 2024年4期

左斌，王仁忠，陶宇，王敏

(1.苏州市职业大学机电工程学院，江苏苏州 215104；2.纽威数控装备(苏州)股份有限公司，江苏苏州 215153)

0 前言

数控加工中心是一种功能齐全且高效的数控机床[1]，加工过程中数控系统根据被加工零件的工序自动选择并更换合适的刀具，完成零件表面的切削、铣削、钻削等多个工序的加工。数控加工中心的主轴系统是控制刀具旋转以及自动更换刀具的部件，当主轴系统进行刀具更换时需借助松拉刀机构完成刀具松开和夹紧2个动作，而松拉刀机构直接影响刀具的更换速度，因此它是高速铣削机床的研究热点。国内众多学者对松拉刀机构与主轴系统做了相应的研究：于陈江等[2]进行了主轴松刀装置底座变形问题的研究，提高了松拉刀机构的直面锁紧装置的机械性能；何强等人[3]研究了电主轴的单气缸动力不足的问题，实现了双气缸松拉刀装置在电主轴上的应用；吴东阳等[4]对松拉刀过程中主轴轴承的受力进行分析，设计出了浮动缸卸荷结构。以上研究均未考虑主轴系统的性能变化，而在实际生产加工的过程中，主轴系统因刀具频繁更换后常出现无法松刀的情况。为经济高效地解决此问题，需综合分析主轴结构和松刀结构，设计出新型结构以满足主轴系统频繁更换刀具的要求。

TRIZ理论是前苏联科学家ALTSHULLER通过对大量专利和创新方案进行分析得出的创新解决问题方法[5-7]，主要包括八大进化法则、39个通用技术参数、40个发明原理和76个标准解等。AD公理化设计是美国麻省理工学院SUH教授提出的一种逻辑性强的思维方法和工具[8]，主要包括信息公理和独立公理2个公理原则。这些方法的理论研究与应用一直受到国内外学者热捧：刘志峰等[9]应用TRIZ冲突原理构建可拆卸系统物-场模型并提出改进方法；俞斌、陈振华[10]基于AD/TRIZ构建了钢卷开卷装置优化设计流程；刘晓敏等[11]基于AD/TRIZ融合流程设计了海草夹苗机械手创新方案。

本文作者针对数控加工中心频繁更换刀具时出现的松刀力不足、无法松刀的问题，应用TRIZ功能模型和因果链分析找出松刀问题的根本原因，并综合TRIZ冲突原理与AD独立公理提出松拉刀的优化设计方案。

1 主轴松拉刀问题描述

数控加工中心在加工过程中可通过一次装夹完成零件的多个工序加工，但此过程中需选择并更换多把刀具，因此，主轴上刀具的更换是数控加工中的一个重要环节。刀具在更换过程中分为刀具夹紧和松开2个动作，实现该动作的部件为松拉刀机构。在更换刀具时常出现松刀力不足和无法松刀2种情况，其产生原因为：(1)松刀力不足。加工中心完成多次松刀、拉刀后，活塞杆与缸体以面接触的形式运动时不可避免地因多次摩擦而出现发热情况，导致密封圈老化甚至出现裂纹，从而影响密封圈的性能，引起松刀力不足；(2)无法松刀。加工中心的刀具在频繁更换过程中，松拉刀机构需多次完成松开、夹紧动作，导致主轴中碟簧弹性逐渐减小、可靠性降低，致使松拉刀机构运动行程不足、无法松刀。

2 主轴松拉刀问题分析

2.1 系统组件功能分析

目前市面上数控加工中心主轴松拉刀的动力源多以液压或气动为主，它主要由前缸盖、后缸盖、油缸、活塞杆、密封圈、拉杆、碟簧、主轴等组成，如图1所示。主轴松刀时，液压油进入油缸的右腔，推动活塞杆向前移动并与拉杆接触，此时主轴中的碟簧对拉杆产生反向作用力，随着液压油的压力持续增大，活塞杆推动拉杆继续向前移动直至拉钉松开，实现主轴松刀；主轴拉刀时，油缸中的右腔压力为零，活塞杆在弹簧作用下完成复位，同时主轴在碟簧的作用下推动拉杆向后运动完成拉刀。

图1 某数控设备主轴松拉刀结构

运用TRIZ系统组件工具对主轴松拉刀功能组件分析，主轴松拉刀的超系统组件、系统组件和子系统组件见表1。工程技术系统是主轴松拉刀，其功能为松开和夹紧，对主轴松拉刀组件两两之间的相互关系进行分析，建立相互关系矩阵，如表2所示。其中，组件间存在相互作用关系用“+”表示，组件间不存在相互作用关系用“-”表示，同一组件间不做比较。通过相互关系矩阵可以更加直观地掌握各个组件间的作用。

表1 主轴松拉刀组件分析

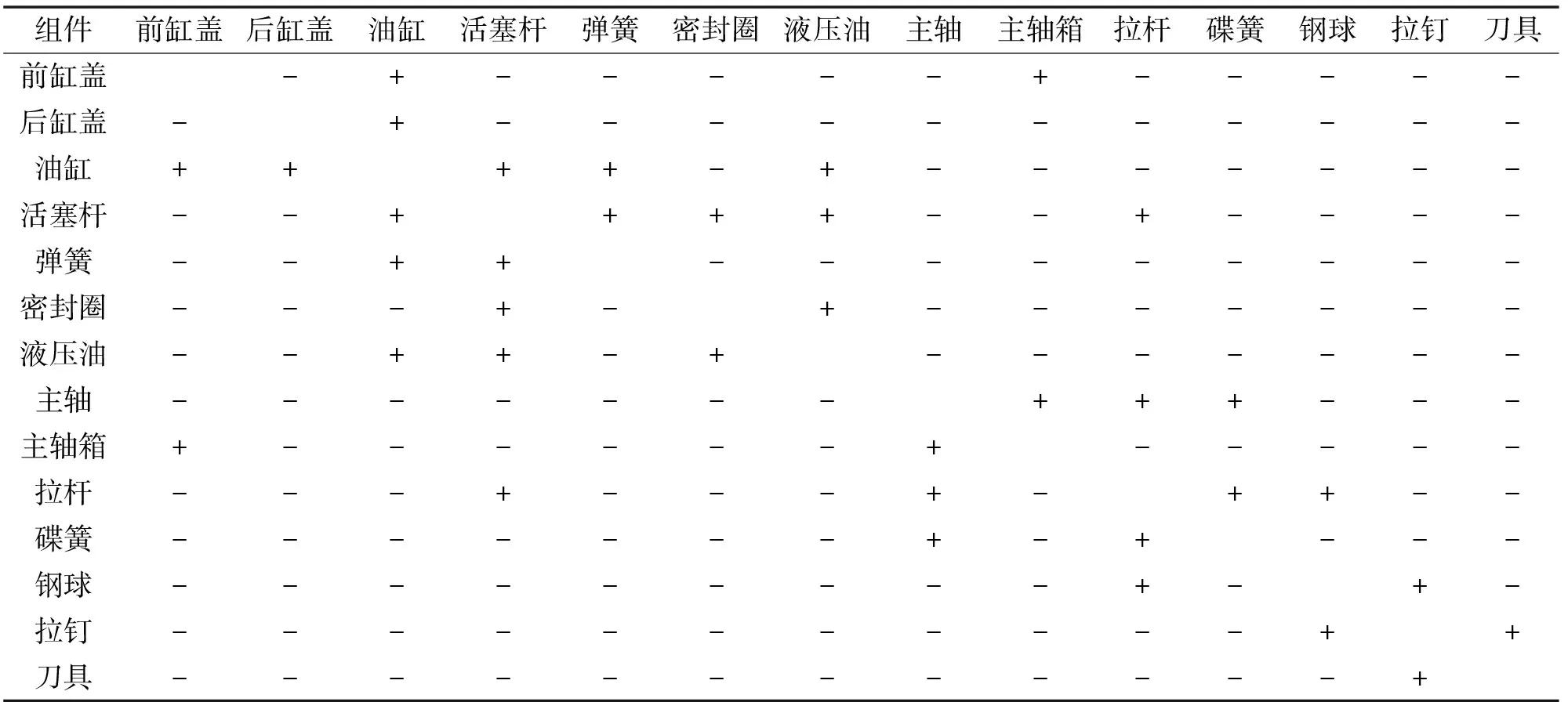
表2 主轴松拉刀相互关系矩阵

根据表1和表2建立主轴松拉刀的功能模型，如图2所示。可知：松拉刀的动作是通过活塞杆推动拉杆实现，活塞杆的运动是利用液压油和弹簧驱动，因此，可初步判断出影响松刀的原因是活塞杆强度、液压油的压力和弹簧强度。

图2 主轴松拉刀功能模型

2.2 系统因果链分析

分析图2判断松刀故障的初步原因，更深层次原因还需进一步挖掘。因果链分析工具可帮助全面识别系统组件以及超系统组件的各种问题，找出根本原因。文中主要探讨的问题是数控加工中心主轴系统无法正常松刀，因此围绕松刀故障进行系统因果链分析，如图3所示。

图3 主轴松拉刀因果链分析

分析图3得出松刀故障主要由松刀力不足以及拉杆未到位所引起的，进一步分析挖掘出更深层次的原因为：(1)打刀缸密封性差；(2)弹簧力过大；(3)活塞杆和拉杆尺寸小；(4)碟簧运动次数多；(5)油缸、主轴间有灰尘、杂质等进入；(6)刀具断裂；(7)材料老化；(8)主轴温升。

结合主轴松拉刀的实际使用情况，针对上述分析所得的关键问题提出初步解决思路，将问题分为3类进行阐述：第一类，通过优化原有配置即可解决的问题：将O形密封圈更换成唇形密封圈提高密封性能解决问题(1)；增加活塞杆和拉杆的直径提高材料刚度解决变形问题(3)；选择优质性能的材料、改进油缸、增加主轴间的防尘装置解决问题(2)(5)(7)；主轴作为数控机床的核心部件，其设计过程经过严谨的计算，其温升产生的误差可通过温度补偿或冷却方式解决问题(8)。第二类，属于系统组件且不易解决的问题：加工中心的主轴需要多次更换刀具，碟簧作为主轴的常用配置不可避免地需要多次被压缩和释放，对它改进较为困难，涉及问题(4)。第三类，超系统问题(6)不作此次解决问题的研究对象。

3 主轴松拉刀问题解决

3.1 运用TRIZ工具生成方案

根据因果链的分析所得到的根本原因中，问题(4)为主轴碟簧多次运动导致碟簧性能降低，影响主轴松刀精度，属于改进较为困难的问题，在此将运用TRIZ工具寻找解决方案。首先将碟簧与拉杆2个物质转化为物场模型，然后运用76个标准解寻找解决方案。碟簧在较大作用力下推动拉杆使刀具夹紧，属于“有效”模型。主轴碟簧经长期压缩后压缩量变小，致使主轴松刀距离减少，因而松刀失败，此时物场模型属于“有效-效应不足”的模型，如图4所示。该物场模型可应用TRIZ理论中的第2类标准解来增强不足效应：运用标准解S2.1，在模型中增加一个“机械场F2”和另一个物质“松刀杆S3”形成链式物场模型，即在活塞杆的前端增加松刀杆物质弥补主轴松刀距离以确保松刀顺利，此时物场模型变为“有效”模型，如图5所示。

图4 效应不足的拉杆物场模型

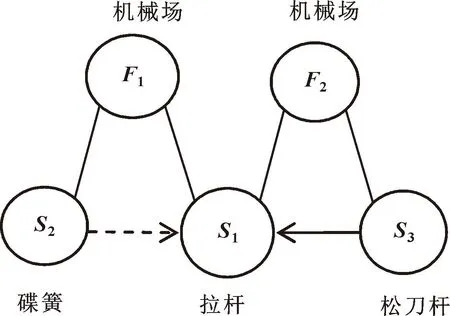
图5 有效的拉杆物场模型

根据改进后的物场模型设计新型的主轴松拉刀初始方案(见图6)：在活塞杆前端增设松刀杆结构，并通过螺纹连接自由调整松刀杆与活塞杆间的距离，在液压作用下活塞杆带动松刀杆共同推动拉杆压缩碟簧完成主轴松刀，从而解决碟簧性能降低所导致的主轴松刀失败的问题。

图6 主轴松拉刀初始方案

3.2 运用AD独立公理判断方案

依据初始方案的结构功能需求与设计参数构建两者之间的表达式，如式(1)所示：

(1)

式中：FR1为松开拉杆功能矢量；FR2为调节拉杆功能矢量；DP1为活塞杆参数；DP2为松刀杆参数。

实际操作中，依据初始方案在活塞杆前端增设松刀杆结构时，无法直接调节松刀杆与活塞杆的移动距离，需拆下松拉刀整个机构才能进行调节，即功能矢量FR1和功能矢量FR2相关，两者间产生了耦合，故原始设计矩阵A为

A矩阵中的子元素表示功能需求到设计参数间两元素的关联程度，1表示两者间存在关联，0表示两者间弱关联或无关联。

根据AD独立公理原则可知，松拉刀机构在移动活塞杆和调节松刀杆距离时，两者间功能不能相互影响，即两者间应该是非耦合的，但此时活塞杆和松刀杆的功能之间产生了耦合，说明原始改进方案不可行，故需消除A21，使得A21=0 。为消除“松开拉杆”和“调节拉杆”两功能之间的相互影响，可借助TRIZ冲突原理将其转化为物理矛盾问题，并利用空间分离原理进行问题求解，形成优化方案：在空间上将松刀机构分为松刀杆调节区和活塞杆移动区，活塞杆移动区设计成环形套筒置于外部，可调节的松刀杆移动区呈包围状态，松刀杆与活塞杆之间通过螺杆固定，如图7所示。首先根据碟簧的压缩量预先调整松刀杆与活塞杆的距离，完成松刀杆调节区的调整。然后利用液压推动活塞杆移动完成主轴松刀的单独控制，从而很好地解决了“松开拉杆”和“调节拉杆”两者之间的矛盾。此时A矩阵变成一个对角矩阵，满足AD独立公理设计要求，方案可行。

图7 主轴松拉刀优化方案

4 主轴松拉刀优化方案落地实施

4.1 主轴松拉刀机构理论分析

(1)主轴松刀力计算

数控加工中心在铣削被加工零件表面时会伴随着切削力F[12]，切削力可分解成3个相互垂直的切向力Fz、径向力Fr、轴向力Fx。通过数控机床手册查找，得到切削力F的公式：

(2)

(3)

根据数控机床设计手册相关资料以及数控机床的实际使用情况确定相关参数：ap为背吃刀量，粗加工时可达8～10 mm；af为每齿进给量，取值为0.1～0.3 mm；d为铣刀直径，取20 mm；aw为铣削宽度，取100 mm；Z为铣刀齿数，取5；x、y、z分别为0.86、0.72、-0.86；Cp为系数，取68.2；δHB为零件的布氏硬度，取190HB。将相关参数代入式(2)中得到最大切削力。

对称铣削时，切向力Fz与水平走刀力Fh、竖直走刀力Fy、轴向力Fx之间的关系有：

(4)

整理式(4)得轴向力Fx：

(5)

根据文献[12]可知，铣削分力系数K1取值为0.80～0.90，代入式(5)得Fx的曲线如图8所示。可知：K1参数相同时，螺旋角ω与主轴轴向力Fx成正比；螺旋角相同时，K1参数与主轴轴向力Fx成反比。因此，当K1参数值最小、ω=45°时轴向力最大，此时Fx=9 179 N。

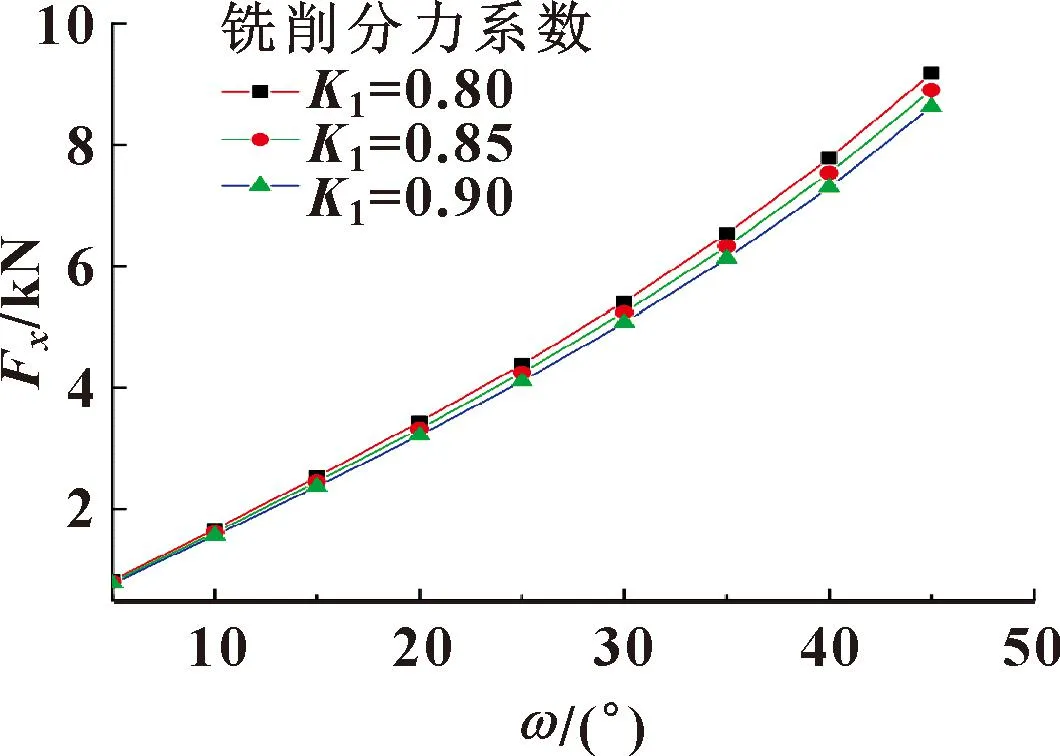
图8 主轴轴向力曲线

同时，数控加工中心在钻削过程中产生的切削力F可根据式(6)计算：

F=309dKpf0.8

(6)

式中：f为每转进给量；Kp为修正系数；d为刀具直径。

很显然加工中心在钻削时所产生的切削力远小于铣削时所产生的切削力，故主轴的拉刀力取决于铣削力。加工中心在加工各种零件时，选取不同的加工参数会使切削力不同，在文中所选参数下得出的拉刀力为9 179 N，然而在松刀时拉杆会进一步压缩碟簧以实现刀柄脱离拉爪，因此松刀力比拉刀力大一倍可确保松刀顺利，故松刀力为18 358 N。

(2)调整螺杆计算

数控加工中心加工箱体类零件时常需根据工艺要求多次更换主轴刀具，使得主轴上的松刀杆频繁工作。为保证松刀杆正常工作，有必要对松刀杆上的调节螺杆进行计算分析。初步选用合金钢作为螺杆材料，强度等级为8.8级，故螺杆的抗拉强度为800 MPa，屈服强度为640 MPa。由于换刀时主轴碟簧变形量最大，导致碟簧对松刀杆的作用力也最大，故此时松刀杆上的螺杆也承受最大的轴向载荷，其载荷量Fa=18 358 N。若采用6个螺杆均匀分布在松刀杆上，则单个螺杆所受的外力为

Fa1=Fa/6

(7)

由式(7)计算得Fa1=3 060 N，单个螺杆承受的总拉力为碟簧的轴向载荷力和螺杆的残余预紧力之和：

F2=Fa1+0.5σsA

(8)

螺杆危险截面的拉伸强度：

(9)

式中：F2为单个螺杆的总拉力；σs为螺杆的屈服强度；Fa1为单个螺杆所受的外载荷；d0为螺杆的底径。

由式(8)(9)计算得d0约为4.75 mm，选择螺杆底径大于4.75 mm即可，故选择6个M6的螺杆用于固定松刀杆。

4.2 主轴松拉刀机构仿真分析

(1)几何建模

由主轴松拉刀机构的优化方案可知：新型松拉刀机构主要由油缸、活塞杆、松刀杆、螺杆和法兰盖组成。主轴换刀时通过液压油驱动活塞杆向前移动，活塞杆通过法兰盖与松刀杆固定连接，从而带动松刀杆向前，推动拉杆完成松刀。根据主轴松拉刀的理论分析以及查阅相关资料得出松拉刀机构的主要设计参数如表3所示[3]。

表3 松拉刀机构的主要设计参数

利用SolidWorks软件的拉伸、旋转、扫描切除等功能对各部件进行建模并装配[13]，通过工具栏中的“干涉检查”命令对松拉刀机构进行检查，结果显示无干涉，判定该模型符合装配要求，其装配见图9。

图9 松拉刀机构优化设计模型

(2)有限元分析

松刀时主轴的轴向反力直接作用在松刀杆上，若松刀杆的强度和刚度不足则会影响主轴松刀，故对其进行静力学分析。首先定义松刀杆的材料为45钢，密度为7 850 kg/m3，弹性模量为2.1×105MPa，屈服强度为220 MPa。基于曲率进行网格划分，最大单元为10 mm，最小单元为2 mm。在松刀杆的前端面设置固定约束，松刀杆的大径右端面处施加轴向力18.4 kN进行仿真计算，结果如图10、11所示。可知：松刀杆在左端面约束条件下最大的应力为45.24 MPa，小于材料的屈服强度；最大变形量靠近载荷处，约为6.995 μm，变形量小，符合结构设计要求。

图10 松拉杆应力分布

图11 松拉杆位移分布

4.3 松拉刀机构试验研究

(1)试验指标及方法

根据上述优化方案，制作了新型松拉刀机构并安装在卧式加工中心主轴上，如图12所示。分别将主轴拉力计、主轴松刀量具安装在加工中心BT50主轴上，通过调节液压站的液压力进行不同工况下的主轴松刀试验，如图13所示。

图12 松拉刀实物结构

图13 松拉刀测试

为验证主轴松拉刀机构的性能及工作可靠度，以松刀成功率为指标开展松拉刀试验，松刀的成功率是指松刀时未出现脱落和松刀力不足的概率。松刀的成功率u为

u=1-t/z-q/z

(10)

式中：t为脱落的刀具；q为松刀未到位次数；z为松刀试验总数。

试验采用正交试验法，选取具有3个水平的试验因素，分别为液压力、打刀量、拉刀力，见表4。松刀试验每组进行3次，共9次，具体方案见表5。

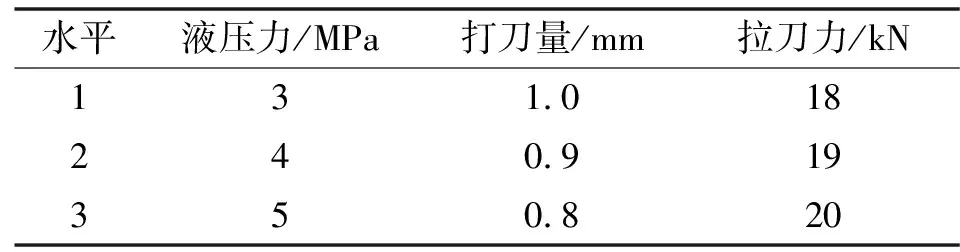
表4 因素水平

表5 松拉刀机构试验方案及结果

(2) 试验结果及分析

由表5可知，3种试验下的液压力因素A影响松刀成功率为72.33%、93.33%、95.67%；打刀量因素B影响松刀成功率为89.00%、85.67%、85.67%；拉刀力因素C影响松刀成功率为92.33%、86.33%、82.67%。为找出最优的试验方案，需对试验结果进一步进行方差分析，如表6所示。

表6 试验结果分析

由表6中的方差指标S可得：液压力A因素对松刀的成功率影响最大，打刀量B因素对松刀的成功率影响最小，其最优的因素组合为A3C1B1，即液压力5 MPa、拉刀力18 kN、打刀量1.0 mm。为验证最优组合的合理性，对松刀机构进行多次测试，统计各指标的平均值。结果表明：主轴在夹刀状态下，拉杆左端面与主轴端面的距离约为156 mm；松刀状态下，均能完成松刀，松刀的行程大于9 mm。