面齿轮车齿加工研究与试验验证

2024-03-14张新成曹雪梅韩正阳蒋闯

机床与液压 2024年4期

张新成，曹雪梅，韩正阳，蒋闯

(河南科技大学机电工程学院，河南洛阳 471003)

0 前言

面齿轮传动是一种与渐开线圆柱齿轮啮合的齿轮传动，具有体积小、质量轻、轴向安装误差敏感度低、传动比大[1-4]等优点。因其独特的分流-汇流传动结构，被广泛应用于直升机主减速器等传动系统中，应用前景广阔。

面齿轮的制造是面齿轮传动领域的一个关键技术问题。李政民卿等[5-6]设计并研制了国内第一台面齿轮插齿机，对面齿轮传动开展了大量研究，主要包括：面齿轮的几何设计、面齿轮加工基本原理及仿真分析等。YANG、TANG[7]提出了使用插铣组合的方法加工面齿轮，通过Vericut仿真与实验证明了该方法的可行性。郭辉等人[8-10]提出了面齿轮滚刀加工方法，设计了球形滚刀，并通过试验进行验证，同时还对面齿轮磨齿进行了大量研究。WANG等[11-12]分析了五轴数控铣床加工面齿轮的机制，推导了铣刀方程，研究了安装误差对加工精度的影响，提出了面齿轮加工参数的补偿方法。

面齿轮磨齿常用的加工方法有插齿、滚齿、铣齿，存在加工效率低、刀具制造成本高等问题，已经成为面齿轮推广应用的瓶颈。

车齿使用切削刃加工，可采用较高的切削速度且齿面连续展成，具有较高的加工效率和精度。圆柱齿轮车齿加工效率是插齿的3～5倍[13]。GUO 等[14]根据车齿刀与工件之间的相对位置和相对运动，建立了齿轮齿面计算模型，完成了直齿轮和斜齿轮的车齿加工算例分析。CHEN 等[15-16]以曲面共轭原理为基础，在无理论刃形误差的前提下提出了直齿圆柱齿轮车齿刀的结构设计方法。GUO 等[17]基于空间交错轴齿轮啮合原理研究了车齿加工机制，对加工直齿轮的斜齿车齿刀进行了设计。目前对车齿的研究主要集中在圆柱齿轮上。

本文作者分析面齿轮车齿加工原理，建立刀具数学模型以及面齿轮车齿加工数学模型，推导刀具与面齿轮的齿面方程。将渐开线齿轮共轭的面齿轮齿面作为基准面，构造车齿齿面的偏差齿面，分析车齿刀齿数、螺旋角和前角对齿面的影响规律。使用数控车齿机床加工面齿轮，使用齿轮检测中心检测齿面，验证车齿加工模型的正确性。

1 面齿轮车齿加工运动分析

图1所示为车齿运动示意，将车齿刀的回转轴线与待加工面齿轮回转轴线的公垂线方向定义为偏置调整方向，H为初始偏置距，β为刀具螺旋角。

H=NOg·sinβ

(1)

式中：NOg为切削点至工件轴心的距离。

图1中：N为切削点，vs为刀具线速度矢量，v1为工件线速度矢量，二者矢量之和vs1是沿面齿轮齿廓方向的相对速度。刀具与工件分别按照角速度ωt、ωg绕各自轴线旋转，并且满足齿数比。在此基础上，通过逐渐减小偏置距H，并使车齿刀沿其轴向同步进给。2种运动相互配合，保持车齿刀的切削刃与面齿轮的齿廓在加工点相切，并沿面齿轮齿线方向进给，直至加工完成。

图2所示为面齿轮车齿加工机床模型。调整B轴使刀具和工件轴交角为90°；C轴为刀具旋转轴，A轴为工件旋转轴，刀具与工件分别以角速度ωt和ωg旋转，转动速度满足传动比，以实现分齿运动；刀具沿X轴的进给实现齿深方向的加工，在切削过程中X轴位置保持不变，通过多次进给以达到实际切深位置；Y轴和Z轴的联动使刀具沿齿长方向移动。

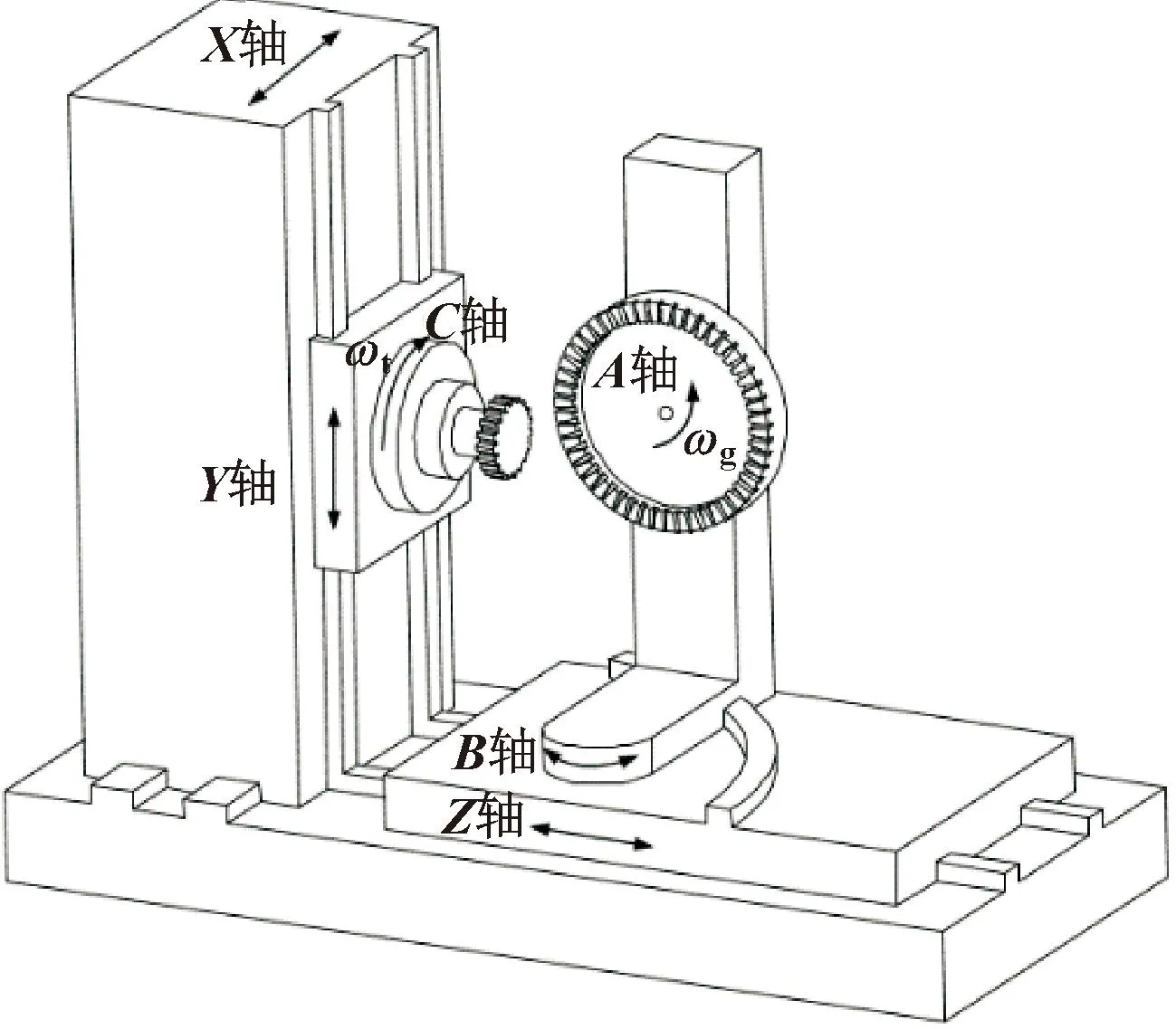
图2 面齿轮车齿机床示意

2 刀具数学模型

2.1 刀具方程

图3所示为车齿刀模型，其由前刀面、侧后刀面、顶面、侧刃和顶刃组成，刀具侧面为渐开螺旋面，切削刃为前刀面与渐开螺旋面的交线[14]4。

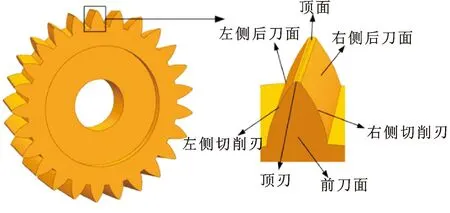
图3 车齿刀模型

图4所示为刀具渐开线齿廓，S1(o1-x1y1z1)为刀具运动坐标系，p1为渐开线起点。曲线p1p2为切削刃工作齿廓，展成面齿轮工作齿面；曲线p2p3为刀尖圆角，展成面齿轮过渡齿面。p2为工作齿廓与刀尖圆角分界点。

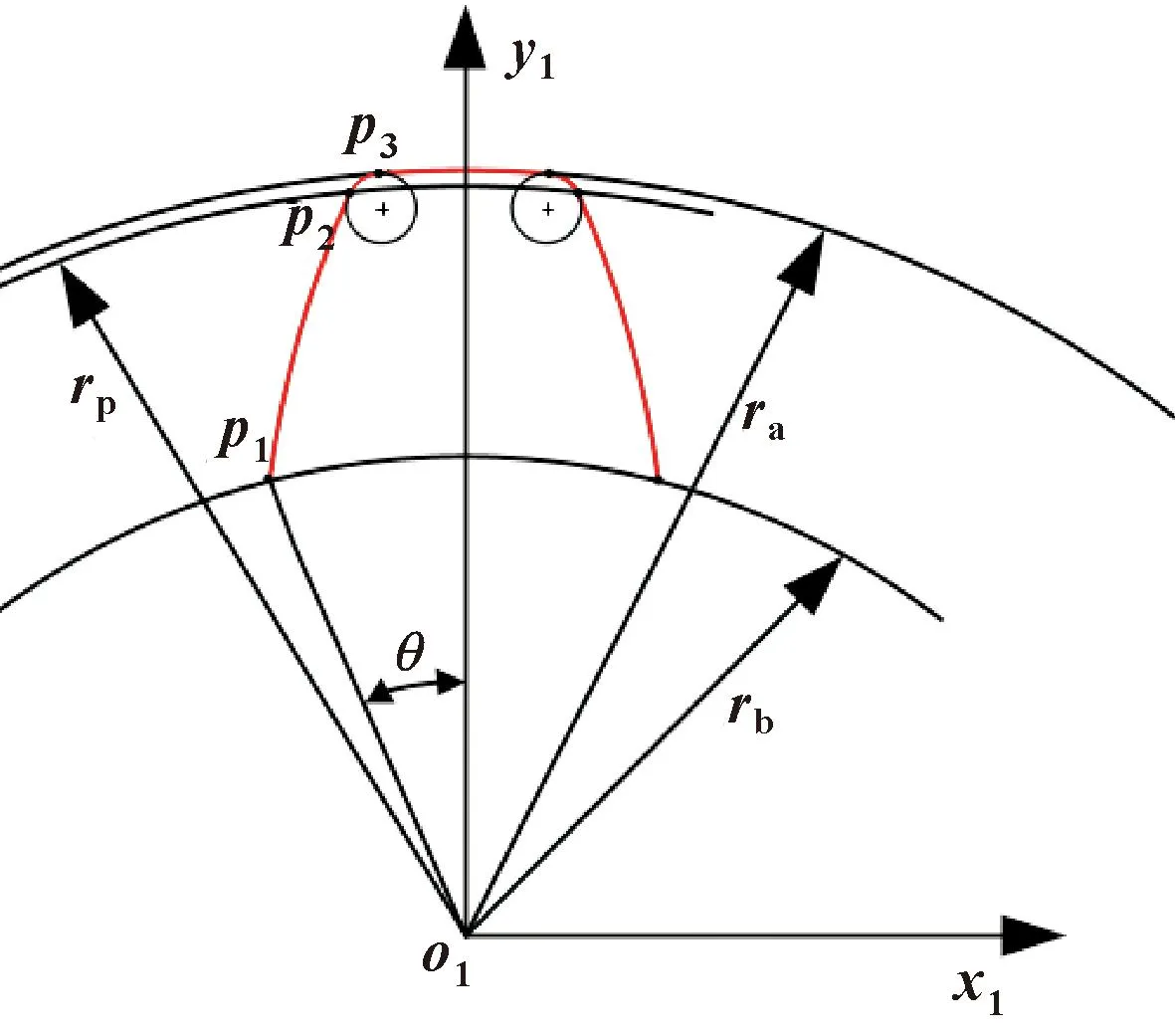
图4 刀具齿廓

在坐标系S1(o1-x1y1z1)中刀具工作齿面表示为

r1(φ，ψ)=

(2)

其中：

A=φ-θ

0≤φ≤tanαp

αp=arccos(rb/rp)

θ1=arcsin[rb/(ra-rc)]

P=rdcotβ

式中：φ为渐开线展角参数；ψ为平面齿廓沿轴线作螺旋运动的旋转角度；rp为o1p2之间的半径；ra为齿顶圆半径；rb为基圆半径；rc为刀尖圆角半径；αp为点p2处压力角；αt和zt分别为刀具压力角与齿数；P为螺旋参数；rd为分度圆半径；Sa=1为右侧齿面，Sa=-1为左侧齿面；Td=1为右旋刀，Td=-1为左旋刀。

2.2 刀尖圆角方程

刀尖圆角如图5所示，rc为刀尖圆角半径，oc为刀尖圆角圆心，左右两侧切削刃关于y1轴对称。

图5 刀尖圆角示意

在坐标系S1(o1-x1y1z1)中刀尖圆角表示为

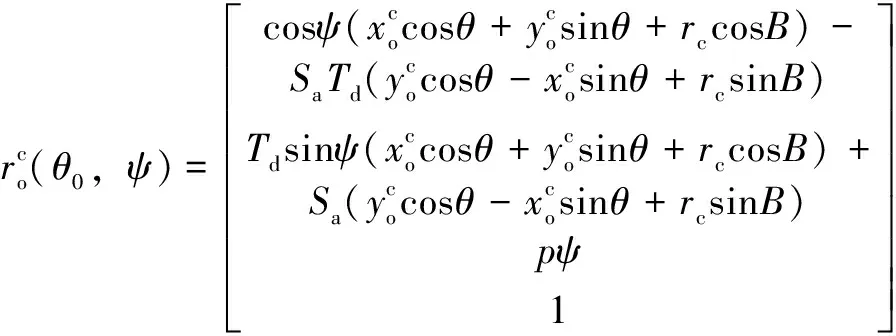
(3)

其中：

B=θ0+θ2-θ

θ2=tanαp-π/2

2.3 前刀面方程

与插齿、铣齿、磨齿等加工方法不同，车齿为刀具切削刃展成齿面，切削刃为前刀面与刀具齿面的交线。图6所示为刀具轴截面，z1轴为刀具旋转轴，在坐标系S1(o1-x1y1z1)中前刀面方程为

(4)

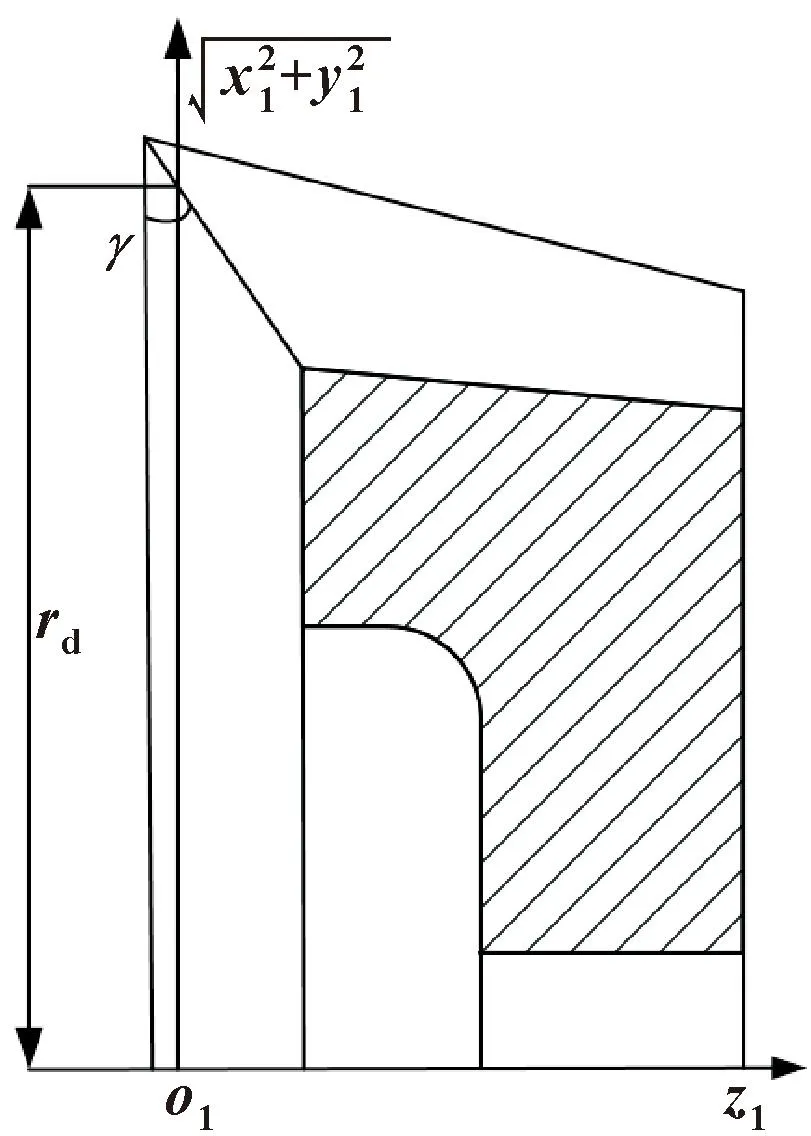
图6 刀具轴截面

式中：(x1,y1,z1)为刀具面位矢；γ为刀具前角；rd为刀具分度圆半径。

3 面齿轮车齿加工模型

3.1 面齿轮车齿展成运动

根据刀具与工件的相对运动关系，建立图7所示的车齿运动模型。S1(o1-x1y1z1)为与刀具固连的动坐标系，绕刀具轴线z1旋转，当前转角为φt；Sn(on-xnynzn)为刀具固定坐标系，与刀具初始位置重合；S2(o2-x2y2z2)为与工件固连的动坐标系，绕工件轴线z2旋转，当前转角为φg；Sm(om-xmymzm)为工件固定坐标系与工件初始位置重合。

图7 车齿展成运动模型

在展成过程中，刀具与工件不仅绕各自轴线转动，刀具还应沿面齿轮径向移动，运动方向与其轴线夹角为β。rg为刀具与工件的相对位移，rd为刀具与工件之间的轴间距。

工件转角与刀具转角关系为

φg/φt=zt/zg

(5)

式中：φg、φt分别为工件与刀具转角；zg、zt分别为工件与刀具齿数。

根据面齿轮车齿刀具与工件的运动关系，刀具齿面在工件坐标系S2(o2-x2y2z2)中表示为

r2(φ,ψ,rg,φt)=M2mMmnMn1r1(φ,ψ)

(6)

式中：

3.2 面齿轮齿面方程

啮合方程有微分几何解法和工程解法2种，文中选择微分几何法构建啮合方程。

偏导矢∂r2/∂φ和∂r2/∂rg表示在工件动系S2(o2-x2y2z2)齿面上的2条不同方向的切线[1]106-107，二者的向量积为齿面法矢N1，φt为广义运动参数。对三变量(φ，rg，φt)求偏导矢，建立啮合方程：

(7)

如图8所示，在工件旋转投影面上划分网格节点，X为工件的轴向，H为工件的径向。沿齿长方向取m个节点，齿高方向取n个节点，节点在旋转投影面位置方程为

(8)

图8 旋转投影

式中：(x2(ij)，y2(ij)，z2(ij))为工件齿面点坐标。

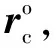
表1为面齿轮基本参数，图9所示为计算得到的齿面网格点。

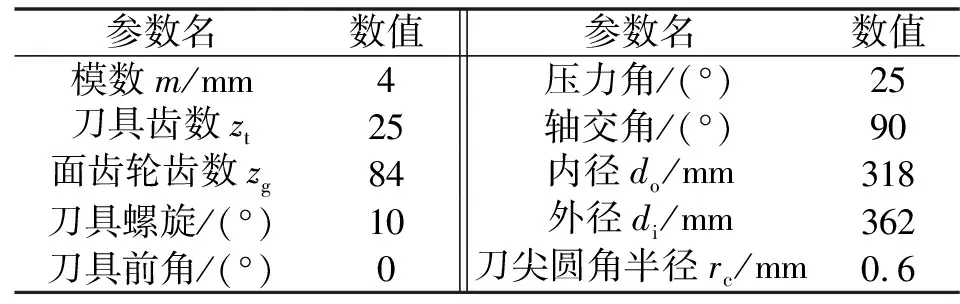
表1 齿轮参数

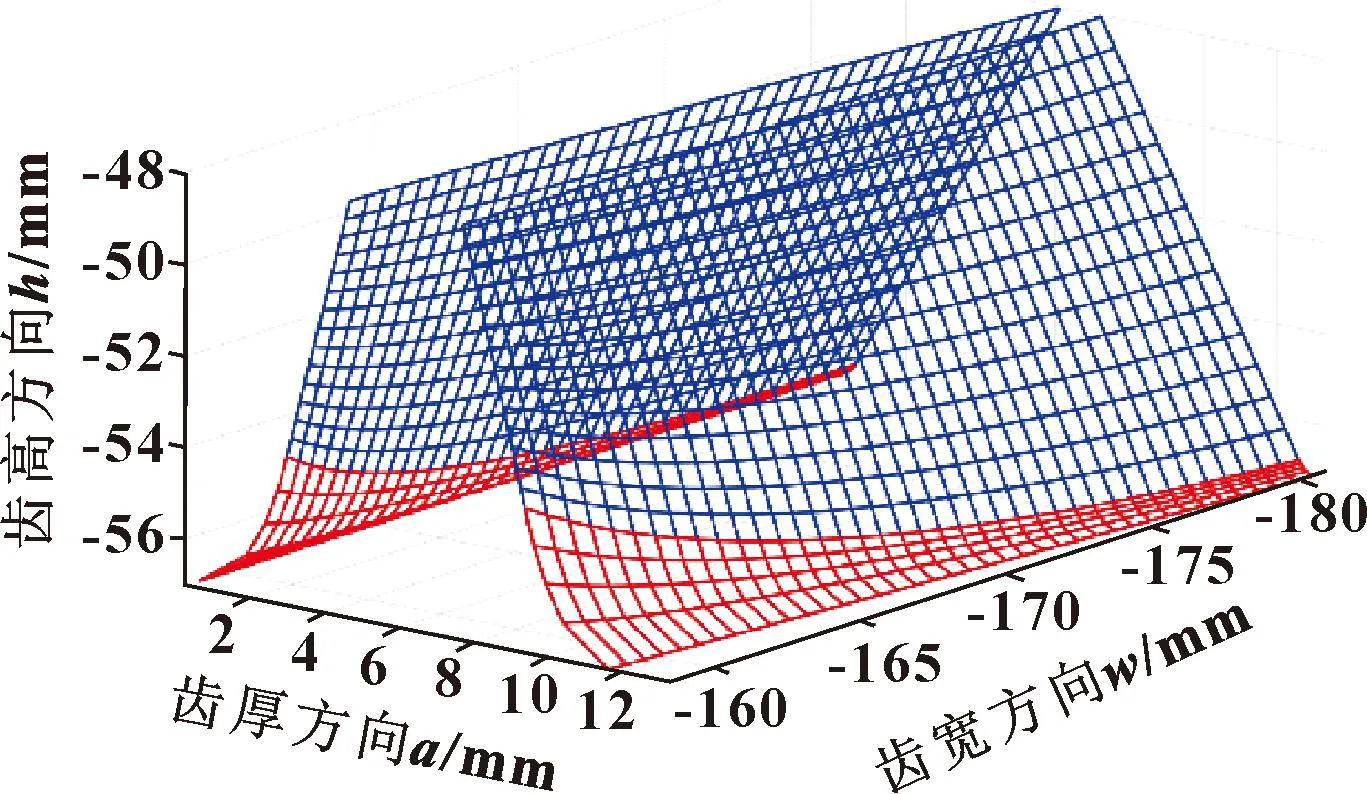
图9 齿面网格

4 刀具对齿面拓扑结构的影响

4.1 齿面偏差

渐开线圆柱齿轮共轭的面齿轮齿面作为基准齿面Σ0，车齿加工的面齿轮齿面为Σ2，Σ0与Σ2在轴截面上对应点的法向距离定义为偏差齿面[16]。齿面对应点的偏差为

e(i，j)=(r2(i，j)-r0(i，j))·n0(i，j)

(9)

式中：r2为Σ2的齿面位矢；r0为Σ0的齿面位矢；n0为基准齿面点的单位法向量；i和j表示轴截面上齿面点所在的行数和列数。

4.2 车齿刀螺旋角对齿面的影响

正交直齿面齿轮左右齿面对称，文中选择右侧齿面构建齿面偏差拓扑图。车齿刀齿数为22、螺旋角分别为5°和12°的齿面拓扑偏差如图10所示。

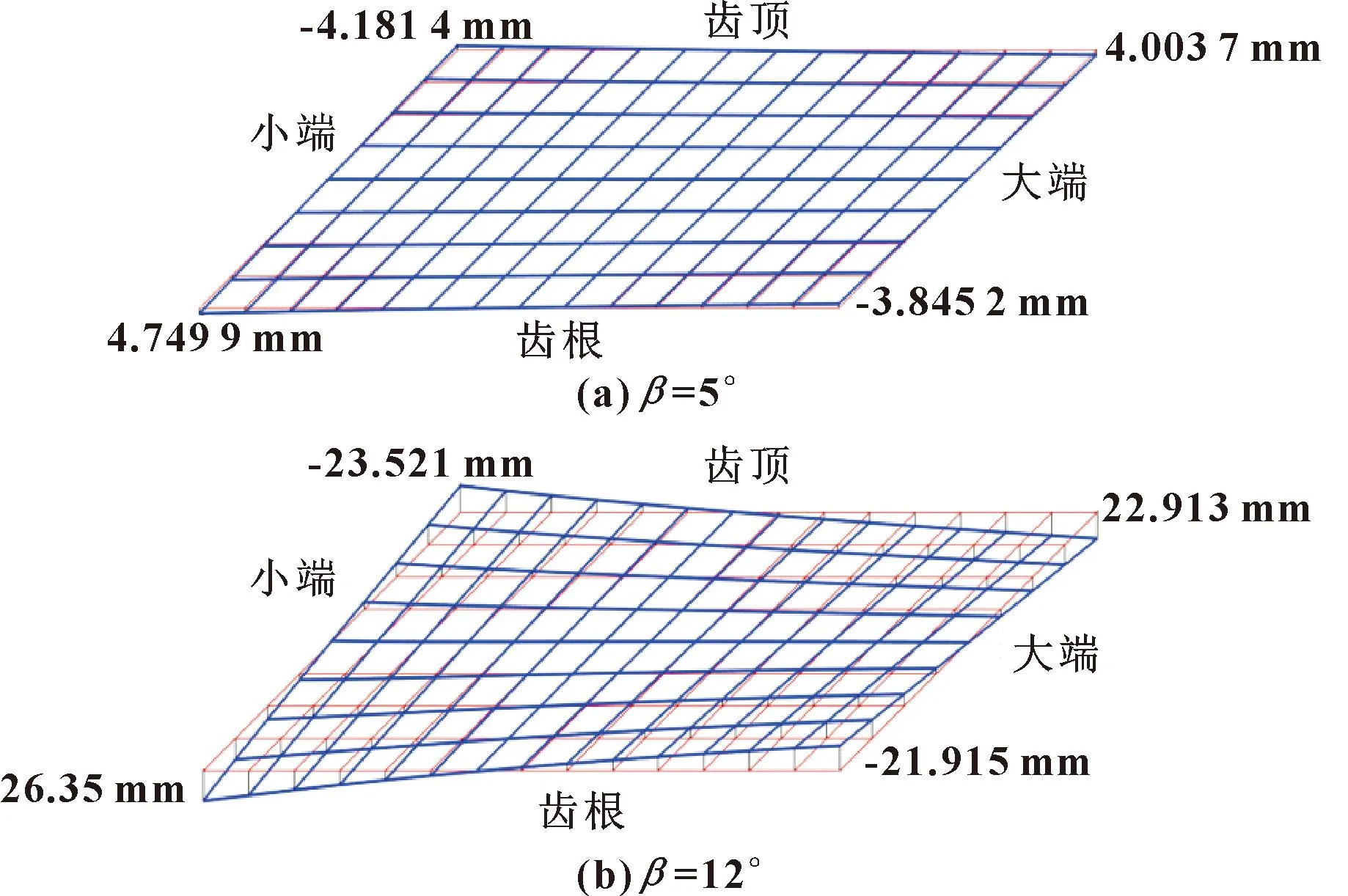
图10 车齿刀螺旋角对齿面的影响

由图10可知：小端齿根和大端齿顶高于基准面，而小端齿顶和大端齿根低于基准面，齿面拓扑偏差为马鞍形，当与配对小轮啮合时，小端齿根和大端齿顶会出现干涉现象。随着螺旋角的增大，偏差值增大，干涉愈加严重。

图11所示为小轮施加30 N·m转矩，刀具螺旋角为5°和12°时对应的面齿轮从啮入到啮出的承载印痕图。当螺旋角为5°时，在小端齿根和大端齿顶出现应力集中，即边缘接触；当螺旋角为12°时，在小端齿根和大端齿顶啮合时出现严重的干涉现象，齿面工作区没有承载印痕，与齿面偏差分布一致。综合图10、11可知，随着螺旋角的增加，齿面干涉程度增加，瞬时接触线即接触区变小，接触迹线与齿顶的夹角减小。

4.3 车齿刀齿数对齿面的影响

保持车齿刀螺旋角为12°不变，车齿刀齿数分别为23、25的齿面偏差如图12所示。

图12 车齿刀齿数对齿面的影响

对比图10(b)和图12可知：随着刀具齿数的增加，小端齿根和大端齿顶的干涉程度降低，小端齿顶和大端齿根偏差值增大。

图13所示为小轮施加30 N·m转矩，车齿刀螺旋角为12°，刀具齿数分别为23、25时对应的面齿轮从啮入到啮出的承载印痕。对比图11(b)和图13可知：随着刀具齿数的增加，齿面干涉程度减小，由于小端齿顶和大端齿根偏差值增大，接触迹线与齿顶线夹角增加，瞬时接触线长度减小。通过增加刀具齿数可以有效增加齿面的鼓形修正量，修正齿顶和齿根的干涉。