碟簧装置恢复力模型及其在自复位RC剪力墙中的应用
2021-09-23徐龙河肖水晶
陈 曦,徐龙河,肖水晶
(北京交通大学土木建筑工程学院,北京 100044)
传统的钢筋混凝土(RC)剪力墙结构满足“大震不倒”的设防要求,但在强烈地震作用下,RC剪力墙底部会产生严重的损伤,结构残余变形较大[1],从而导致震后结构的修复难度大,甚至需要推倒重建,造成巨大的社会经济损失[2]。为了减小结构在震后的损伤和残余变形,使其功能快速恢复,国内外学者对具有自复位性能的结构及构件进行了广泛的研究,恢复力一般可通过预应力筋、形状记忆合金(SMA)、碟形弹簧等提供。预应力筋在自复位RC剪力墙中具有广泛的应用,Kurama等[3 − 4]首先提出了一种无粘结后张预应力自复位剪力墙,放松墙板与基础之间的连接,通过结构自重和预应力筋为墙体提供恢复力,研究表明这种自复位剪力墙具有较好的变形能力,且基本没有残余变形,但耗能能力差;Lu等[5]提出了在两侧墙脚处设置水平缝、墙体内设置预应力钢绞线提供恢复力的自复位剪力墙,试验和模拟结果均表明其自复位性能良好。SMA材料由于其具有良好的形状记忆效应、超弹性及高阻尼性,在自复位领域受到了较高的关注,Qiu和Zhu[6 − 7]提出了一种使用新型SMA支撑的自复位钢框架结构,通过振动台试验和数值研究表明其自复位效果显著,结构残余变形及损伤较小。基于碟形弹簧使用灵活、承载力高、占用空间小等特点,徐龙河等[8 − 10]和Xiao等[11 − 12]提出一种自复位RC剪力墙,在两侧墙脚处设置碟簧装置提供复位能力,并通过墙体自身变形或附加摩擦耗散地震能量;试验和模拟结果表明自复位RC剪力墙具有良好的自复位能力和延性,可减小墙体的残余变形和墙脚的损伤程度。
碟簧装置主要由复位系统和耗能系统两部分组成,装置构造如图1所示。耗能系统包括内外摩擦板、内焊挡板、外管和预紧螺栓;复位系统包括内管、组合碟簧和碟簧挡板[12]。碟簧装置的试验结果表明,当无附加摩擦且无预压时,叠合的碟簧间存在接触摩擦,使得碟簧装置受压的力-位移关系呈三角形,当有附加摩擦和预压时,碟簧装置受压的力-位移关系呈旗形,受拉呈矩形,而在现有的分析模型中,无法直接模拟碟簧装置的这种特性。为了精确地模拟碟簧装置和自复位RC剪力墙的力学性能,本文对碟簧装置的工作原理和力学特性进行分析,提出了一种适用于描述碟簧装置力学特性的恢复力模型,利用MSC.Marc平台对其进行二次开发,并与碟簧装置在往复荷载作用下的试验结果进行了对比,验证了恢复力模型的有效性。基于碟簧装置的恢复力模型,建立了自复位RC剪力墙的数值模型,对其在低周往复荷载下的滞回性能进行模拟分析,结果表明,自复位RC剪力墙的滞回性能与试验结果吻合较好,并进一步分析了碟簧装置参数对其滞回性能的影响。

图1 碟簧装置构造图Fig.1 Configuration of the disc spring device
1 碟簧装置性能
1.1 复位系统力学特性
碟簧组合形式主要有叠合组合、对合组合和复合组合三种,改变叠合组合的数量可以控制组合碟簧的承载力,改变对合组合的数量可以控制组合碟簧的变形量[8 − 9]。为同时满足碟簧装置承载能力和变形能力的要求,组合碟簧采用复合组合形式。
组合碟簧在受压时,叠合碟簧锥形叠合面之间会产生摩擦力,摩擦力会改变组合碟簧的刚度[13]。当组合碟簧受压时,摩擦力阻碍变形增加,使碟簧实际刚度增大;卸载时,摩擦力阻碍变形恢复,使碟簧实际刚度减小。碟簧装置受压时,考虑摩擦力影响时,组合碟簧的荷载FR由式(1)确定:

式中:fM为碟簧锥面间的摩擦系数;fR为碟簧承载边缘处的摩擦系数;n为叠合组合碟簧片数;式(1)中,用于加载时取正号,卸载时取负号。FS为单片碟簧承受的荷载,FS与位移的关系为[14]:

式中:Ed、µ分别为碟簧材料的弹性模量和泊松比;t、h0分别为碟簧厚度和压平时的变形量;Δ为单片碟簧的变形量;M1为与碟簧内、外径比C=D/d相关的系数,D、d分别为碟簧的外径和内径;M1由式(3)确定:

单片碟簧刚度KS为:
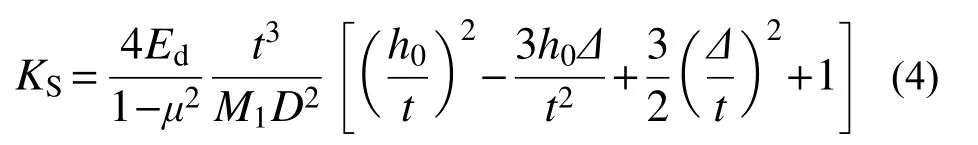
1.2 耗能系统力学特性
耗能系统主要通过内外管上的摩擦板发生相对滑动耗散能量,内外摩擦板分别固定在内焊挡板外侧及外管内侧,利用预紧螺栓连接内管和外管并挤压摩擦板,调节螺栓的扭矩可控制耗能系统提供的摩擦力F0。图2为耗能系统的滞回曲线,其形状近似为矩形。当外荷载F≤F0时,内外摩擦板相对静止。当外荷载F>F0时,内外摩擦板发生相对滑动,提供摩擦力F0且保持不变,系统刚度为0。

图2 耗能系统滞回曲线Fig.2 Hysteretic curve of the energy dissipation system
1.3 碟簧装置力学性能
当碟簧装置所受荷载较小时,其竖向变形主要为外管的弹性变形及各部件之间的接触变形。受压时,随着荷载增大,外管与内管之间发生相对滑动,外管推动碟簧挡板使组合碟簧压缩,卸载时,碟簧提供恢复力使碟簧装置复位。受拉时,碟簧装置内外管随着受拉加卸载发生相对滑动,若在碟簧装置中设置附加摩擦,其耗能系统被激活后,能耗散地震能量,因此,碟簧装置受拉时仅展现出摩擦耗能的特性。
图3为耗能系统和复位系统共同工作时碟簧装置的滞回模型。定义碟簧受压为正向,受拉为负向。由于碟簧只可承受压力,不承受拉力,因此,碟簧装置受拉和受压的力-位移关系曲线不对称。

图3 碟簧装置滞回模型Fig.3 Hysteretic model of the disc spring device
碟簧装置所受外荷载F为0时,由于组合碟簧中存在预压力P0,因此组合碟簧存在一定的初始压缩变形δ1,由式(5)确定:

式中:K1为组合碟簧受压加载刚度;K0为碟簧装置初始刚度,由式(6)确定:

式中:KO为外管轴向刚度;EO、AO和LO分别为外管的弹性模量、等效横截面积和有效长度。
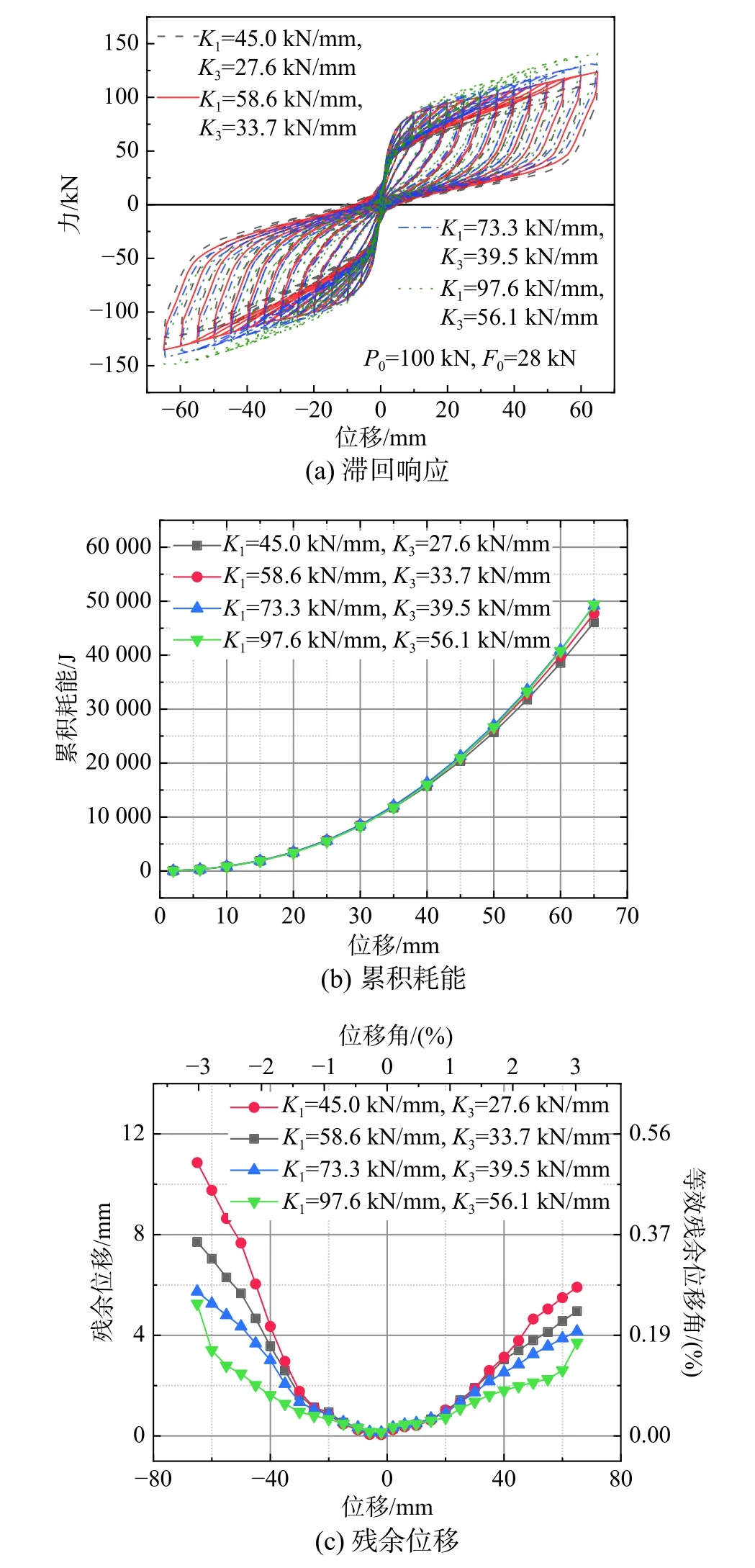
OA段,开始受压至内外管即将发生相对滑动。碟簧装置内外管之间未开始相对滑动,此时外荷载F AB段,受压后内外管开始发生相对滑动至最大变形阶段。此时碟簧装置所受外荷载F≥P0+F0,耗能系统和复位系统均处于激活状态。耗能系统中内外管相对运动通过摩擦片耗散能量,并提供与加载方向相反的摩擦力F0且保持不变。该阶段内外管发生相对滑动,此时碟簧装置的刚度主要为组合碟簧的刚度,考虑碟簧间摩擦力影响的碟簧装置整体刚度K1表示为: 式中,i为碟簧对合组数。 BC段,受压加载停止至即将卸载的过渡阶段。此阶段内外管之间无相对滑动,碟簧间的摩擦力与摩擦装置附加摩擦力由最大静摩擦力逐渐减小到0并反向逐渐增大到最大静摩擦力,碟簧装置变形主要为外管的弹性变形,碟簧装置过渡刚度为K2=K0。 CD段,受压卸载至碟簧恢复到初始状态阶段。卸载阶段碟簧装置受外力减小,组合碟簧提供恢复力挤压碟簧挡板,推动外管使内外管之间再次发生相对位移,耗能系统和复位系统处于激活状态,碟簧装置进入复位阶段。此时碟簧装置的刚度主要为组合碟簧的刚度,卸载过程中,碟簧间摩擦力反向使碟簧装置卸载刚度降低,考虑碟簧间摩擦力影响的碟簧装置整体刚度K3表示为: DA′段,碟簧恢复到初始状态至碟簧装置受拉内外管即将发生相对滑动阶段,此阶段组合碟簧已经恢复到初始状态,不再提供恢复力,内外管之间相对位移为0。碟簧装置由受压状态转变为受拉状态,内管与外管之间不发生相对滑动,此时受拉荷载F A'B'段,内外管开始发生相对滑动至受拉最大位移阶段。此阶段组合碟簧不提供恢复力,组合碟簧保持初始预压状态,碟簧装置受拉荷载F≥F0,内管与外管直接发生相对滑动,耗能系统通过摩擦耗能,摩擦力大小恒为F0,方向与加载方向相反,碟簧装置刚度为0。 B'C'段,受拉加载停止,碟簧装置进入受拉卸载阶段,摩擦力反向,内外管未发生相对滑动,变形主要为内外管的弹性变形,碟簧装置刚度为K0。 C'D'段,受拉卸载至初始位置阶段,内外管之间发生相对滑动,耗能系统摩擦力反向,大小为F0,碟簧装置刚度为0。 根据前文所述碟簧装置各阶段工作原理和滞回响应,碟簧装置各阶段恢复力F(t)与位移δ(t)对应关系归纳如下: 碟簧装置可能出现的三种滞回曲线如图4所示。当同时施加碟簧预压力和附加摩擦力时(P0>0,F0>0),碟簧装置受压的滞回曲线呈旗形,受拉呈矩形。当只施加碟簧预压力,无附加摩擦力时(P0>0,F0=0),碟簧装置受压的滞回曲线呈旗型,受拉时恢复力恒为0。当无碟簧预压力,无附加摩擦力时(P0=0,F0=0),碟簧装置受压的滞回曲线呈三角形,受拉时恢复力恒为0。 图4 碟簧装置不同情况的滞回曲线Fig.4 Hysteretic curves of the disc spring device under different conditions 为了更准确地模拟碟簧装置及自复位RC剪力墙,本文基于MSC.Marc平台,通过USPRNG用户单元对碟簧装置恢复力模型进行了二次开发。计算过程中,MSC.Marc主程序在当前增量步开始时,将上一增量步中弹簧单元两端节点的位移差值δ、速度dδ及其他标识属性传递给USPRNG,从而判定碟簧装置所处的加、卸载阶段,并计算更新后的弹簧单元恢复力F和刚度K。 Xiao等[12]对带有耗能系统的碟簧装置进行了拟静力试验,本文选取其中2个工况对碟簧装置恢复力模型的准确性进行验证,试验中碟簧装置预压力P0均为68.6 kN,耗能系统提供摩擦力F0分别为28.4 kN和34.3 kN。相同加载条件下,碟簧装置试验与利用恢复力模型模拟的滞回曲线对比如图5所示。由图5可知,碟簧装置模拟与试验结果吻合较好。卸载阶段模拟曲线与试验曲线存在一定误差,这是由于碟簧装置恢复力模型为分段式,未能很好考虑各阶段的平滑衔接,略高估了卸载阶段的碟簧承载力,略低估了碟簧装置的耗能能力。 图5 碟簧装置模拟与试验滞回响应对比Fig.5 Comparison of hysteretic responses between simulation and test of disc spring devices 表1为碟簧装置试验与模拟在不同加载位移下恢复力F和对应等效粘滞阻尼比ζeq对比及相对误差。与试验结果相比,附加摩擦力分别为28.4 kN和34.3 kN时,各级加载位移下恢复力模型模拟的恢复力最大相对误差分别为7.57%和2.95%,等效粘滞阻尼比最大相对误差分别为6.93%和13.99%。结果表明,碟簧装置恢复力模型可以有效预测碟簧装置的滞回响应和耗能能力。 表1 碟簧装置模拟与试验结果对比Table 1 Comparison of simulation and test results of disc spring devices 利用已开发的恢复力模型,分析设计参数碟簧预压力P0、附加摩擦F0、碟簧间摩擦系数fM和碟簧刚度KS对碟簧装置性能的影响,除特别注明外,其余设计参数固定,分别为:P0=100 kN、F0=28 kN、KS=42.75 kN/mm、fM=0.03、fR=0.15、i=5、n=5。图6给出了不同设计参数碟簧装置的滞回曲线。 图6 不同设计参数碟簧装置的滞回曲线Fig.6 Hysteretic curves of disc spring device with different design parameters 图6(a)为不同P0对碟簧装置性能的影响,可以看出,只增大P0不会改变滞回环的形状和面积,对构件的耗能能力无明显影响,碟簧装置加卸载刚度均不变,但会增加受压时组合碟簧的激活力及激活位移,同时增加相同加载位移下碟簧装置的承载力,减小残余位移,提高碟簧装置的自复位性能。但P0对碟簧装置设计行程有一定影响,当组合碟簧的规格、数量及组合方式不变时,增加碟簧预压力会降低碟簧装置设计最大压缩行程,但可通过改变碟簧规格和增加对合组数等方式提高碟簧装置的设计行程。图6(b)为不同F0对碟簧装置性能的影响,由图可知,只增加F0不改变碟簧装置各阶段的刚度,但可使滞回环的面积增大,提高碟簧装置的耗能能力,且显著提高碟簧装置在受拉状态下的承载力,同时使碟簧装置残余位移增大。fM对碟簧装置性能有一定的影响,如图6(c)所示,其他设计参数不变时,随着fM的增大,碟簧间摩擦力增大,组合碟簧耗能增大,同时碟簧装置卸载刚度减小,降低碟簧装置的自复位性能,可通过在碟簧间涂润滑油降低接触面的摩擦系数,从而调节碟簧装置的自复位性能及耗能能力。图6(d)为不同KS对碟簧装置性能的影响,由图可知,其他设计参数不变时,碟簧装置受压加载刚度K1和卸载刚度K3随KS的增大而增大,碟簧装置的承载力和自复位性能提高。 碟簧装置安装在自复位RC剪力墙两侧,通过上下连接板、高强螺栓及预埋件与墙体连接[9 − 10]。水平荷载作用下,剪力墙两侧碟簧装置一侧受压一侧受拉,卸载时,复位系统提供恢复力使墙体回到初始位置,碟簧装置在往复运动中通过耗能系统耗散地震能量。 在MSC.Marc中建立如图7所示的自复位RC剪力墙数值模型。混凝土材料采用Von Mises屈服准则和各向同性硬化准则,单轴受压本构关系采用修正的Kent-Park模型[15]以考虑箍筋对混凝土的约束作用。钢筋材料采用Von Mises屈服准则和随动硬化准则,单轴受拉本构关系采用汪训流模型[16]。 图7 自复位RC剪力墙有限元模型Fig.7 Finite element model of self-centering RC shear wall 墙体采用分层壳单元模拟,边缘约束区等关键部位纵筋采用桁架单元进行模拟,加载梁与地梁采用壳单元模拟,墙体与地梁及加载梁之间固接,模拟时通过连接处共用节点实现。碟簧装置采用弹簧单元模拟,并通过已开发的恢复力模型模拟碟簧装置的力-位移关系,其中关键参数K0、K1、K3由式(4)、式(6)~式(8)确定。 Xiao等[12]对自复位RC剪力墙进行了低周往复加载试验,本文在MSC.Marc中建立了与文献[12]中试件SC-SW3设计参数相同的有限元模型,试件SC-SW3中碟簧装置的F0为34.3 kN,P0为95.1 kN,材料参数及加载制度根据文献[12]中提供的试验数据确定。 图8为自复位RC剪力墙试验与模拟滞回曲线对比,整体吻合良好,数值模型能够比较准确模拟自复位RC剪力墙的滞回响应。表2为试件SCSW3试验和模拟在各级加载位移下承载力对比,可以看出,正向加载和负向加载的承载力最大相对误差分别为18.44%和7.41%。加载前期模拟曲线较试验曲线的承载力误差稍大,主要原因在于模拟中混凝土单元达到极限应变后完全失效,无法考虑试验中损伤未剥落的混凝土对墙体承载力的贡献,当加载位移大于35 mm后,误差均小于10%。试件正向加载与负向加载时的残余位移均能与试验吻合。 图8 试验和模拟滞回曲线对比Fig.8 Comparison of hysteresis curve between simulation and tests 表2 试验与模拟承载力误差Table 2 Bearing capacity error between test and simulation 图9为自复位RC剪力墙试验和模拟在每个加载位移下滞回耗能对比,可以看出,数值模拟与试验结果基本一致,由于正向加载时的承载力误差,导致加载位移为15 mm和20 mm时相对误差较大,其余加载位移下,滞回耗能相对误差均小于10%。因此,本文中的应用碟簧装置恢复力模型的数值模型可以有效模拟自复位RC剪力墙的滞回特性、自复位性能及耗能能力。 图9 试验和模拟滞回耗能对比Fig.9 Comparison of hysteretic energy dissipation between simulation and test 为了研究不同设计参数的碟簧装置对自复位RC剪力墙滞回响应,累积耗能和残余位移的影响,本文对10个不同工况的自复位RC剪力墙进行模拟分析。图10(a)为碟簧装置不同P0和F0对自复位RC剪力墙滞回曲线、累积耗能和残余位移的影响。可以看出,自复位RC剪力墙承载力随F0和P0的增大而增大。随着F0的增大,自复位RC剪力墙的滞回曲线越来越饱满,耗能能力增强。图10(b)为F0和P0对累积耗能的影响,可以看出,整体耗能受P0变化影响较小,整体累积耗能随F0的增大而显著增大。碟簧装置刚度一定,P0为100 kN时,F0分别为14 kN、28 kN、35 kN、42 kN时,自复位RC剪力墙最终累积耗能分别相比F0为0时提高25.0%、50.5%、62.9%、75.1%。F0和P0对自复位RC剪力墙残余位移影响明显,由图10(c)可知,在各级加载位移下,卸载后自复位RC剪力墙残余位移随F0的增大而增大,随P0的增大而减小,与附加摩擦力和碟簧预压力的比值F0/P0成正相关。F0为42 kN时,P0由100 kN增大到150 kN,F0/P0由0.42减小到0.28,自复位RC剪力墙的最大残余位移减小40%。因此可通过增大F0提高自复位RC剪力墙的耗能,并通过调节F0/P0控制构件的残余位移。 图11为碟簧装置不同K1和K3对自复位RC剪力墙滞回响应,累积耗能和残余位移的影响。可以看出,自复位RC剪力墙的承载力和第二刚度随碟簧装置刚度的增大而增大,而耗能能力基本不受碟簧装置刚度影响。由图11(c)可知,当构件最大加载位移角小于1.5%时,碟簧装置刚度对构件残余位移影响较小,当加载位移较大时,构件卸载后的残余位移随碟簧装置刚度的增大而减小。因此对于不同的工程需求,碟簧装置设计中可以通过调节碟簧预压力、附加摩擦力和组合碟簧刚度实现自复位RC剪力墙所需的承载力,自复位性能和耗能能力。 图11 K1和K3对自复位RC剪力墙性能的影响Fig.11 Effect of K1 and K3 on the performance of selfcentering RC shear wall 本文提出了一种适用于描述碟簧装置力学性能的恢复力模型,并对其进行二次开发,在低周往复荷载作用下,对自复位RC剪力墙的滞回性能进行模拟,分析不同设计参数的碟簧装置对其滞回响应,累积耗能和残余位移的影响,得到以下结论: (1) 利用所建立的碟簧装置恢复力模型模拟结果与试验结果吻合良好,恢复力最大相对误差为7.57%,等效粘滞阻尼比最大误差为13.99%,验证了恢复力模型的准确性。 (2) 自复位RC剪力墙数值模拟结果与试验滞回行为一致,两者承载力和滞回耗能误差较小,除个别加载幅值下误差较大,其余情况误差均小于10%,应用碟簧装置恢复力模型的数值模型可有效模拟自复位RC剪力墙的滞回特性、自复位性能及耗能能力。 (3) 自复位RC剪力墙的承载力随碟簧预压力、附加摩擦力及碟簧装置刚度的增大而增大;耗能能力随附加摩擦力的增大而增大;残余位移随附加摩擦力的增大而增大,随碟簧预压力和碟簧装置刚度的增大而减小。
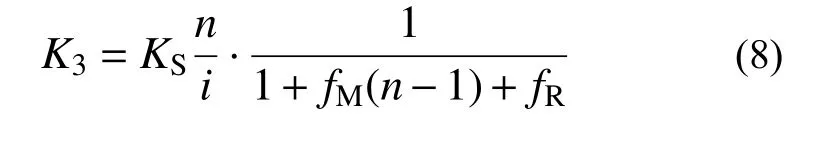
2 碟簧装置恢复力模型
2.1 恢复力模型的建立

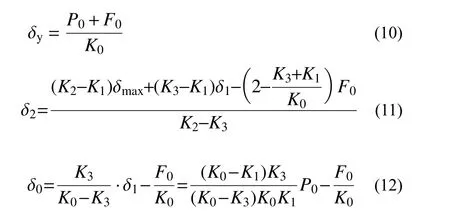
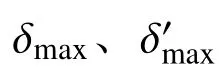

2.2 恢复力模型的二次开发
2.3 恢复力模型试验验证


2.4 碟簧装置设计参数分析

3 碟簧装置恢复力模型在自复位RC剪力墙中的应用
3.1 自复位RC剪力墙数值模型的建立
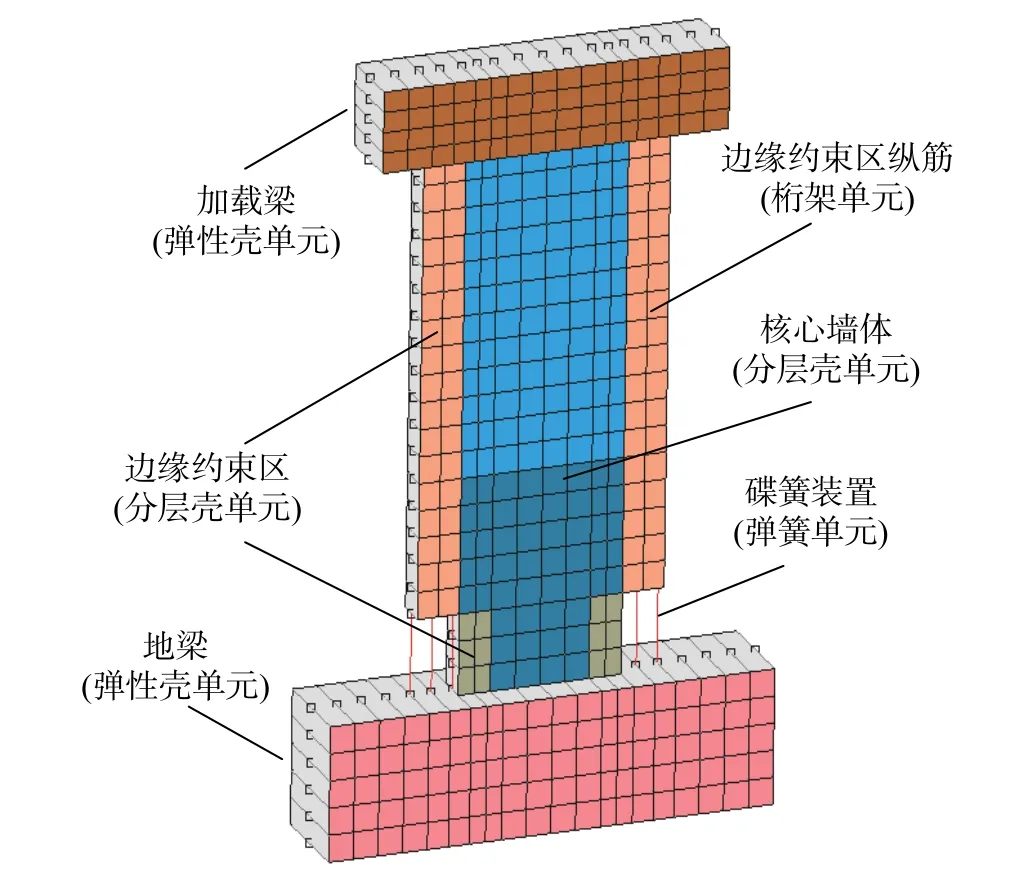
3.2 数值模型验证



3.3 碟簧装置对自复位RC剪力墙抗震性能影响
4 结论
