立式铣床直齿铣刀固有频率研究*
2015-11-28王天任张玲利闻邦椿
王天任 张玲利 李 鹤 闻邦椿
立式铣床直齿铣刀固有频率研究*
王天任 张玲利 李 鹤 闻邦椿
(东北大学 机械工程与自动化学院 辽宁沈阳110819)
铣床刀杆的振动情况直接影响零件的加工质量。将刀杆简化为欧拉梁模型,分别计算了刀杆在不考虑陀螺效应和考虑陀螺效应时的固有频率,并研究了不同的刀杆转速对固有频率的影响。同时考虑了刀杆的悬臂长度和刀杆直径对其固有频率的影响。研究结果表明,在不考虑陀螺效应时,悬臂刀杆的固有频率不会随着刀杆转速而变化。在考虑陀螺效应时,随着刀杆转速的增大,正进动的固有频率会变大而反进动的固有频率会降低。刀杆的各阶固有频率会随着刀杆悬伸长度的减小而增大,随着直径的变大而变大。
铣刀 固有频率 陀螺效应 刀杆悬伸长度 刀杆直径
伴随着制造业的快速发展,铣削成为一种越来越重要的加工方式。铣削加工已不断的被应用于航空、汽车、船舶及核电等工业领域[1]。但是在实际的铣削过程中,由于刀具和工件的刚性作用,实际的加工过程中会出现不稳定现象[2-3],这种不稳定性会严重影响加工的精度和效率。铣床在加工中出现不稳定现象主要指的是铣削过程中出现的刀具振动现象。因此对于铣床铣刀固有频率的研究意义可见一斑。
本文利用悬臂欧拉梁[4]简化铣刀刀杆,分别计算了在不考虑陀螺效应[5,6]和考虑陀螺效应时刀杆的固有频率。并研究了刀杆的悬伸长度和刀杆直径对其固有频率的影响。研究结果将为铣床刀具的使用和选择提供理论基础。
1 理论模型
1.1 不考虑陀螺效应时悬臂刀杆的固有频率
根据铣刀的几何形状和工作形态,将立式直齿铣刀刀杆简化成等径悬臂梁,将刀杆固定端定为坐标系原点,轴向为进给方向,轴为刀轴线,如图1所示。
在不考虑陀螺效应影响时,悬臂刀杆可以视为欧拉梁,它的振动齐次微分方程为:

式中:v(z,t)为悬臂梁的挠度函数;E为刀杆材料的弹性模量;I为刀杆截面惯性矩;A为刀杆截面积;ρ为刀杆材料密度。

悬臂梁的边界条件为:固定端:该端点被完全固定,因此有位移与转角为零,即:
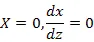
自由端:该端点可以任何方向的运动都不受限制,因此弯矩与剪力等于零即:
将()代入悬臂梁条件[7],得到悬臂梁的固有频率方程为:


根据式(3)求解式(1),得到悬臂梁的各阶固有频率为:
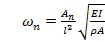
其中:为刀杆悬深长度。根据式(4)可知,在不考虑陀螺效应时,刀杆的各阶固有频率是定值,不随主轴转速的变化而变化。
1.2 考虑陀螺效应时悬臂刀杆的固有频率
当考虑陀螺效应的影响时,刀杆的振动齐次微分方程要加入陀螺力矩,加入陀螺力矩后刀具正进动微分方程为:

反进动微分方程为:
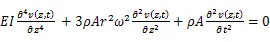
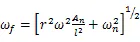
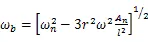
式中:为单位长度的刀杆关于直径的回转半径;为刀杆悬伸长度;E表示刀杆的杨氏模量;A为振型系数:
A1=3.515;A2=22.034;A3=61.7;A4=120.91;



2 刀杆参数对固有频率的影响
2.1 悬臂刀杆参数
表1中给出了悬臂刀杆参数,采用Matlab仿真的方法计算出在考虑陀螺力矩时,刀杆的每阶固有频率随着转速变化的关系。

表1 悬臂刀杆参数
2.2 刀杆的悬伸长度对固有频率的影响
刀杆的悬伸长度是其工作时的一项重要参数,它对刀杆的固有频率具有很大的影响。因此本文通过控制刀杆直径为Φ10 mm时,研究了悬伸长度分别为100 mm和80 mm时,刀杆的固有频率随刀杆转速的变化。通过MATLAB仿真,结果如图2和图3所示。结论表明,在刀杆直径固定时,对于相同的刀杆转速,刀杆的各阶固有频率会随着刀杆悬伸长度的减小而增大。

图2 前两阶固有频率与转速的关系曲线示意图
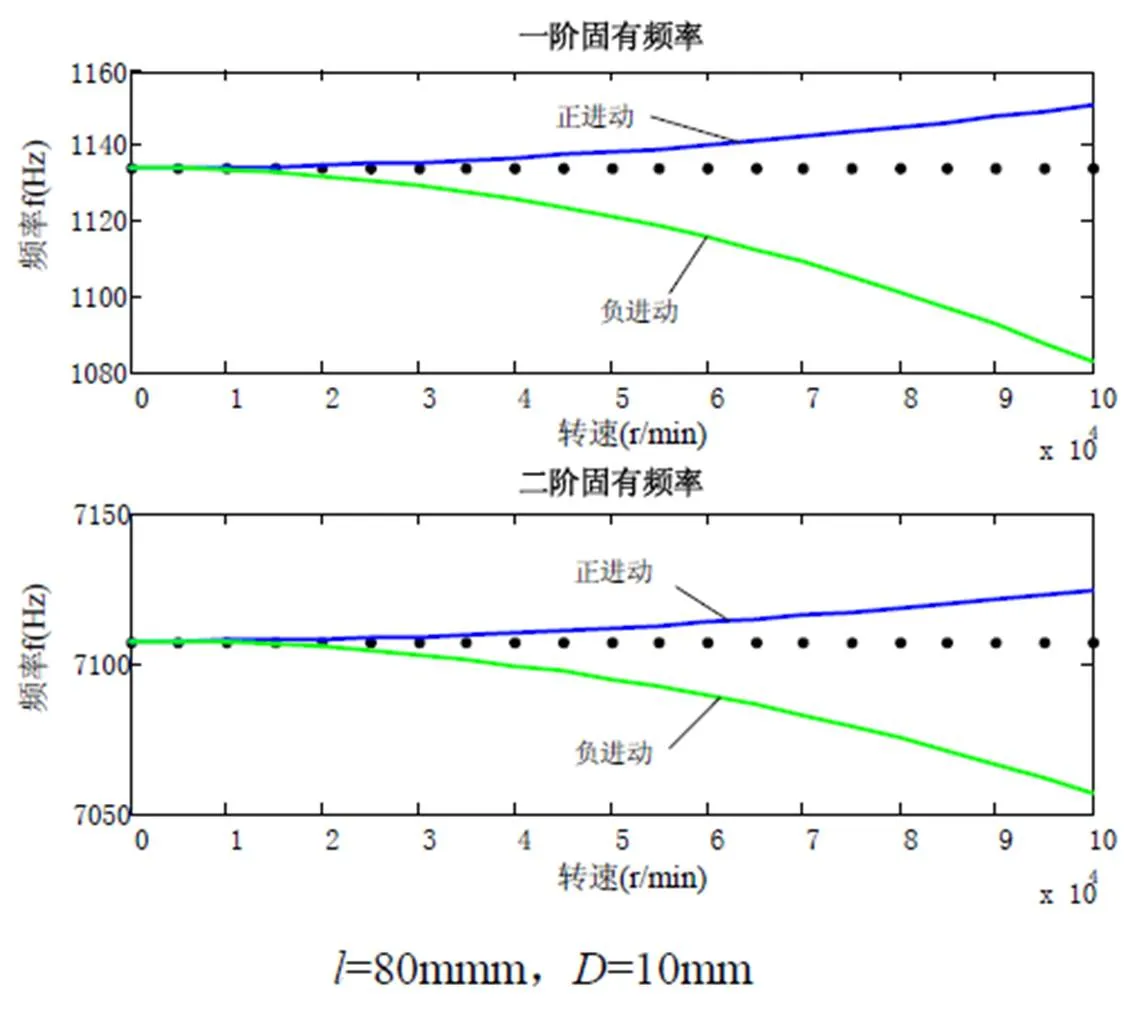
图3 前两阶固有频率与转速的关系曲线示意图
2.3 刀杆直径对固有频率的影响
刀杆直径影响加工前对工具的选择,因此研究刀杆直径对固有频率的影响也是非常必要的。本文通过控制刀杆的悬伸长度为100mm时,研究了刀杆直径分别为10mm和12mm时,刀杆的固有频率随刀杆转速的变化。通过MATLAB仿真,结果如图3和图4所示。结论表明,当悬伸长度一样时,对于相同的刀杆转速,刀杆的直径越大刀杆的各阶固有频率会越大。

图4 前两阶固有频率与转速的关系曲线示意图
3 结语
将刀杆简化为悬臂欧拉梁模型,分别建立了考虑陀螺力矩和不考虑力陀螺矩时刀杆的振动微分方程,并得到刀杆的固有频率。分别研究了转速、刀杆悬伸长度、刀杆直径对其固有频率的影响。研究结论为(1)在不考虑陀螺效应时,刀杆的各阶固有频率是定值,不随主轴转速的变化而变化。(2)考虑陀螺力矩时,在刀杆转速相同的情况下,刀杆的各阶固有频率会随着刀杆悬伸长度的减小而增大,随着刀杆直径的变大而变大。这些将为铣削系统刀杆的使用和选择提供理论依据。
[1] Tlusty.J.ManufacturingProcessanEquipment[M].Engle -wood Cliffs, Upper Saddle River, NJ: Prentice Hall, 2000.
[2] 李欣,李亮等.过程阻尼对铣削系统稳定性的影响[J].振动与冲击,2014.9(33):16-19.
[3] 曹自洋等.考虑犁切力的微铣削颤振稳定域建模与分析[J]制造技术与机床,2003(1):132-136.
[4] 刘彦,周进华.基于欧拉梁理论的管路纵向波功率流简化模型误差分析[J].中国舰船研究,2012.2(5):13-16.
[5] 胡腾,殷国富等.基于离心力和陀螺力矩效应的“主轴-轴承”系统动力学特性研究[J].振动与冲击,2014.8(33):100-108.
[6] 刘伟佳.陀螺效应对转子临界转速的影响[J].吉林师范大学学报,2012(3):47-49.
[7] 屈维德,唐恒龄.机械振动手册[M].北京:机械工业出版社,2005:147-150.
*国家自然科学基金资助项目
编号:51175071
