基于流固耦合的静压转台底部支撑优化

高凌宇，洪荣晶

(南京工业大学机械与动力工程学院，江苏南京 211816)

0 前言

液体静压转台具有摩擦因数低、刚度高、承载能力大等特点，被广泛应用于各种机加工设备中[1]。由于液体静压转台的油膜厚度极小，油腔的微小变形就会引起油膜的较大变化，从而影响静压转台的承载能力；而且，静压转台的底部支撑点处会发生微小应变，影响静压转台的加工精度，因此有必要深入研究静压转台底部支撑布局对油腔变形和底部支撑点应变的影响规律。KOZDERA和 DRBKOV[2]利用Fluent软件研究了环形腔静压轴承的油膜厚度对油膜承载力和油腔压力的影响规律。ZHANG等[3]运用动网格技术，针对双矩形油腔进行了数值模拟。HU 和LIU[4]提出了一种针对液体静压转台的流-固-热耦合模型，研究了不同工作参数对静压转台润滑性能的影响。DHANDE和 PANDE[5]根据流固耦合原理研究了轴承的变形情况。QIN等[6]提出了一种用于解决箔片推力轴承的双向流固耦合模型。张庆锋[7]设计了一种扇形油腔并基于流固耦合模型验证了其可行性。王长飞和周焕林[8]基于萤火虫算法对不同螺栓数量下的结构进行布局优化，优化后结构的孔周应力集中现象均得到明显改善。肖文耀等[9]提出了单亲混沌遗传算法，对螺栓布局进行了优化，克服了传统遗传算法在工程应用上的局限性。王晓婷和刘文光[10]研究了螺栓组布局对承载能力和刚度的影响。

在大型重载静压转台加工过程中，毛坯工件可达上百吨，工件质量通过油膜传递到静压转台的油腔内导致油腔变形，从而对油膜厚度产生影响，降低油膜的承载能力和刚度。在加工重型工件时，底部支撑点附近也会产生微小应变，导致转台加工精度降低。

针对以上问题，本文作者通过建立静压转台流固耦合模型，以得到静压转台在额定负载下油腔的变形量和底部支撑点处的应变量，分析底部支撑点半径和间距对变形和应变的影响规律，确定转台底部支撑布局最佳参数并进行重构。

1 静压转台工作原理及有限元建模

文中研究对象为南京某公司大型静压转台，如图1所示，其工作原理为：通过液压泵将一定压力的润滑油从液压站输送到多个静压油腔内，油液经过封油边回流到回油槽中，再从回油槽排到液压站中完成循环。在导轨与封油边之间形成厚度大约几十微米的油膜，使运动导轨面浮起，保持导轨面与封油边之间为纯液体摩擦状态，可以大幅度降低摩擦阻力和动力消耗。

图1 静压转台外观

静压转台底座如图2所示，在三维建模软件中对转台底座进行建模，模型如图3所示，底座设计了3圈静压导轨，2圈主导轨用于主要外载荷，副导轨起到辅助支撑作用。但由于重载时图3中A区域较薄弱所以不通油，为了保持转台的平衡B区域的3个油腔也不通油，即副导轨起支撑作用的为18个恒压油腔。转台底部支撑结构如图4所示。

图2 静压转台底座

图3 底座建模

图4 底部支撑结构

2 静压转台流固耦合仿真

2.1 流固耦合模型建立

首先建立油膜的模型，为提高网格质量，节约计算时间，利用ICEM CFD将油膜划分成结构化网格后导入Fluent进行仿真，油膜的厚度为0.028 mm，黏度为0.03 Pa·s，油膜网格整体如图5(a)所示，进油口处采用O形剖分如图5(b)所示。

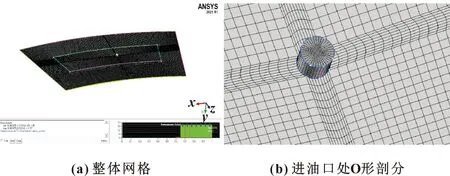
图5 油膜网格

静压转台的油腔由22个恒流式供油油腔和32个恒压式供油油腔构成，因此恒压式供油油腔入口边界设置为压力入口，入口压力值为0.3 MPa，恒流式供油油腔入口边界设置为速度入口，设置为0.1 L/min，2种油腔出口边界条件皆为压力出口，出口压力值为0，其余边界设置为壁面。其中恒流式供油油腔的压力分布如图6所示。

图6 油腔压力分布

2.2 静压转台流固耦合分析

静压转台底座材料为铸铁，密度为7 300 kg/m3，弹性模量为130 GPa，泊松比为0.25，最大外负载约为2×106N(含工作台自重)，通过油膜和油腔之间的流固耦合交界面直接作用在静压转台的主导轨和副导轨上。边界条件设置如图7所示。

图7 底座边界条件设置

油腔的变形云图和底部支撑的应变云图如图8所示，从图8(a)中可知变形区主要集中在主导轨处，最大变形量为8.729 μm。从图8(b)中可知底部支撑点处应变最大为4.926 3×10-5。

图8 静压转台流固耦合分析结果

3 底部支撑结构分析及重构验证

3.1 支撑点半径对静压导轨变形和底部支撑处应变的影响

支撑点半径是影响静压导轨变形和底部支撑处应变的关键因素之一，由于转台一共有4圈支撑点，但是第一圈支撑点处的静压导轨变形较小且分布均匀，所以只考虑后3圈支撑点，分为R2、R3和R3、R4两种不同情况进行分析。s为静压导轨变形量，ε为底部支撑处应变量，表1所示为参数的描述、初始值以及变化范围。

表1 距离参数变量

当保持R4=2 190 mm不变时，静压导轨的变形量s随半径R2、R3的变化如图9(a)所示，当R2在1 280～1 320 mm、R3在1 650～1 700 mm时，静压导轨变形较小；当保持R2=1 340 mm不变时，静压导轨的变形量s随半径R3、R4的变化如图9(b)所示，当R3在1 650～1 700 mm、R4在2 170～2 185 mm时，静压导轨变形较小。

图9 底部支撑半径对变形量的影响关系

当保持R4=2 190 mm不变时，底部支撑处最大应变量ε随半径R2、R3的变化如图10(a)所示，当R2在1 300～1 330 mm、R3在1 670～1 700 mm时，底部支撑处最大应变量ε较小；当保持R2=1 340 mm不变时，底部支撑处最大应变量ε随半径R3、R4的变化如图10(b)所示，R3在1 650～1 700 mm、R4在2 170～2 185 mm时，底部支撑处最大应变量ε较小。

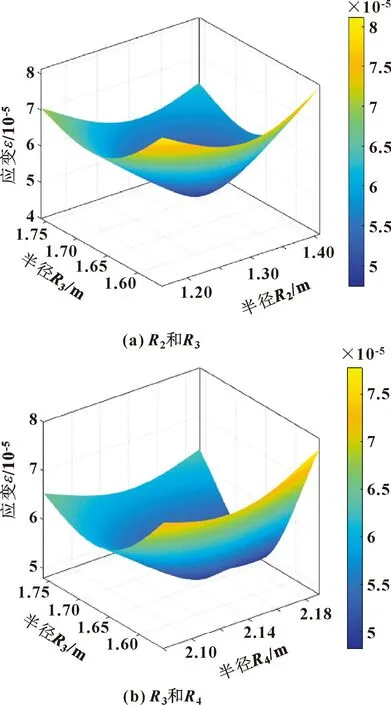
图10 底部支撑半径对应变量的影响关系

综合上述分析，考虑静压导轨变形量和底部支撑处应变量，取R2=1 300 mm、R3=1 680 mm、R4=2 180 mm。

3.2 相邻支撑点夹角对静压导轨变形和底部支撑处应变的影响

相邻支撑点夹角也是影响静压导轨变形和底部支撑处应变的关键因素之一，θ的取值会直接影响底部支撑点的个数。由于第一圈相邻支承点间夹角θ1对静压导轨变形的影响极小，所以分为θ2、θ3、θ43种不同情况进行分析，表2所示为θ的描述、初始值以及变化范围。

表2 角度参数变量

静压导轨的变形量s随θ的变化如图11所示，可知：第二圈相邻支承点间夹角θ2、第三圈相邻支承点间夹角θ3和第四圈相邻支承点间夹角θ4对静压导轨变形的影响显著。

图11 θ对变形量s的影响关系

底部支撑处最大应变量ε随θ的变化如图12所示，可知：当3圈的相邻支承点间夹角取值θ为18°～25°时支撑点处的最大应变量较小。

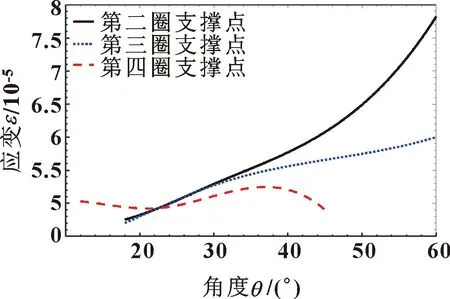
图12 θ对应变量ε的影响关系

综合上述分析，考虑实际加工和现场装配条件等因素，θ值不可过小，且要均匀布置，所以θ2、θ3保持初值不变，取θ4=12°。

3.3 转台重构及验证

根据第3.1、3.2节中优化后的参数，利用SolidWorks三维建模软件重新对转台底座进行建模，并建立流固耦合模型，所有边界条件与重构前一致，重构后的静压导轨变形云图如图13(a)所示，重构后的支撑点应变云图如图13(b)所示。

图13 重构后的结果

对比重构前后的静压导轨变形量云图，发现静压导轨的最大变形量从8.729 μm减小到7.049 μm，降低了约19.25%；对比重构前后支撑处应变量云图，发现应变量从4.926 3×10-5减小到3.458 3×10-5，降低了约29.80%，且应变量分布更加均匀。

4 实验验证

为了验证有限元分析结果的可靠性，以该转台为实验对象，在承载1.6×106N(含工作台自重)的工况下，搭建试验台底部支撑处应变测试系统，如图14所示。

图14 应变测试系统

测试点1、2设置在转台外立面，测试点3、4设置在转台底部平面，每个测试点设置2个垂直分布的应变片，测试2个方向上的应变量。每个测点对应的方向如表3所示。具体布置如图15所示。

表3 应变测点分布

图15 应变片布置

由表4可知：仿真结果和实测结果基本一致，证明了转台底座模型建立的正确性和底部支撑结构优化结果的可靠性，但是也存在一定的偏差。造成偏差的原因有：

表4 底部支撑应变实测值与仿真值对比

(1)应变测量系统存在一定的误差，如应变测试仪精度误差、外部干扰、应变片粘贴不当等因素；

(2)仿真时忽略了油温上升产生的影响，但实际转台工作过程中，即使转台没有转动，油液流经管路和阀门也会导致油温略微升高。

5 结论

文中基于流固耦合的方法对静压转台底部支撑布局进行了重构，重构后油腔变形降低了约19.25%，底部支撑点处应变降低了约29.80%，并通过试验验证了仿真的可靠性。此研究为大型静压转台的底部支撑布局的设计和实际生产提供了理论参考。