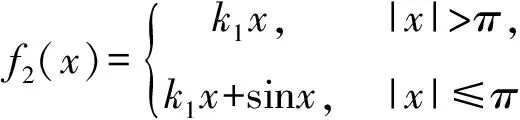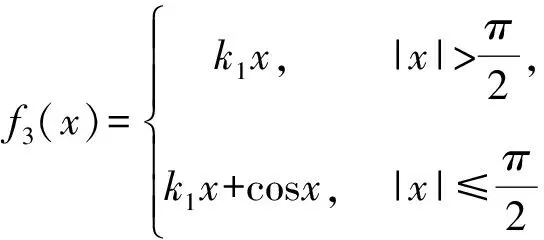问题与征解
2023-01-14
大学数学 2022年6期
问题

(i)证明:PA(m)是以m为变量的多项式;
(ii)证明:PA(m)的阶数degPA(m)是A的相似不变量;
(iii)计算degPA(m),用A的若当块的阶数表示.
问题22(供题者:吉林大学 周鸣君) 设n≥2,Ω∈n是有界区域,
p(x)=xTAx+bTx+c,
其中,A=(aij)是n×n阶实矩阵,x和b是n维列向量,c是常数.若a11a22 解答 问题11(供题者: 复旦大学 严金海) 设f为上的非线性连续函数, 称x0∈为f的严格凹支撑点, 若存在k∈,使得f(x)>f(x0)+k(x-x0), ∀x∈{x0}.类似地, 称x0∈为f的严格凸支撑点, 若存在k∈,使得f(x) 解本解答由张神星(合肥工业大学副研究员,E-mail: zhangshenxing@hfut.edu.cn)提供. (i)当k1 (ii)当k1>k2时,f必有严格凸支撑点, 无严格凹支撑点; (iii)当k1=k2时, 各种情形都有可能. 不难看出,x0是f的严格凹支撑点当且仅当存在k使得 f(x)-kx>f(x0)-kx0,∀x≠x0. 换言之,x0是函数gk(x)=f(x)-kx的唯一最小值点.凸的情形类似. (i)设k1 由于gk是连续函数, 因此它存在最小值. 我们断言, 存在k1 于是k′(dk-c)f(dk)-f(c)k(dk-c),故cdk.因此ck (ii)此时-f满足(i)中的条件, 从而易证. (iii)由(i)最后一段论述可知若f有严格凹或凸支撑点, 则对应的k只能是k1=k2.由此不难得出: f1(x)=k1x+arctanx, 无严格凹和凸支撑点. 供题者点评解答正确, 其将单调性与可列性结合得到唯一性的方法非常巧妙.