不同截面形状的油腔振荡冷却的流动和传热分析

董小瑞，李 达，张 翼，崔 楠，李海鹰

(1. 中北大学 能源动力工程学院，山西 太原 030051； 2. 中国北方发动机研究所，天津 300400)

活塞振荡冷却是一个复杂的传热过程，其流动和换热性能受多种因素影响，如油腔位置[2]、 内流道形状[3]、 机油流量[4]、 机油温度[5]等. 国内外学者对此进行了很多研究，Bush等[6]在管流振荡传热公式的基础上提出了油腔壁面对流换热系数的理论公式，并作为经典公式被用于求解对流换热系数； Yi等[7]设计了振荡冷却数值计算的计算流体动力学(CFD)模型，并得出了机油填充率和换热系数随曲轴转角的变化情况； 张卫正等[8]提出了一种基于动网格和流体体积(VOF)多相流的简化模型，降低了计算难度； 朱海荣等[9]比较了RNGk-ε、 Realizek-ε和SSTk-ω3种振荡冷却湍流模型的计算结果, 得出使用SSTk-ω仿真准确性更高的结论； 邓晰文等[10]提出了一种基于相对位移法的瞬态分析方法，将整个流体域看作运动的刚体进行计算，降低了计算成本； 吴志明等[11]提出了非惯性坐标系的分析方法，并使用该方法进行数值分析，得出了冷却油腔的周向流动和换热特性.

以往的研究往往只针对一种固定截面形状的冷却油腔进行数值分析，并没有考虑不同形状截面的油腔在相同条件下的机油流动和换热的差异. 基于此，本文给出了3种常见截面形状的环形冷却油腔，采用计算成本较小的相对位移法计算了不同截面形状的冷却油腔内部的流动和传热特性，并对比了不同截面形状的冷却油腔的壁面机油分布、 填充率和各壁面换热系数随曲轴转角的变化规律，对活塞冷却油腔的形状设计、 快速验证、 效果对比有一定的参考意义.

1 振荡冷却传热的数学模型

1.1 VOF模型

振荡冷却是一个复杂的流动和换热过程，在分析时需要对分析模型进行简化，将整个计算域简化为仅含机油和空气的计算域，且互不相混. 使用VOF模型进行求解，其控制方程如下

(1)

ρgi+Fi,

(2)

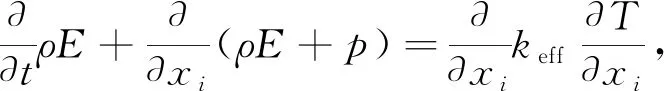
(3)

式中：αq为第q相的体积分数；t为时间；u为速度；ρ为密度；p为单元中的压力；gi为重力加速度；Fi为单元的体力；keff为有效热导率；E为能量；T为温度.

一方面，教师应当正确认识自身角色定位，充分发挥其引导作用和辅助作用，在二胡演奏教学和训练的过程中制订科学合理的训练意志目标，层层递进；另一方面，教师应当引导学生根据训练效果的反馈信息正确分辨技巧的正确有效与否，明确自己的优势及应当改进完善的缺陷，有针对性地进行训练，从而攻克一个个技术难点。

每个控制单元内第q相流体的体积分数有以下3种情况： ①αq=0，即单元内不存在第q相流体； ②αq=1，即单元内只有第q相流体； ③ 0<αq<1，表示单元内有第q相流体，也有其他流体，第q相流体与其他流体之间互不相混，有明显的分界.

1.2 相对位移法

考虑到活塞做规则的往复运动，本文采用文献[10]提出的相对位移法进行活塞振荡冷却的瞬态分析，将整个计算域看作一个刚体作往复运动来模拟振荡效果，将动网格法中固定的入口边界条件(即机油入口和空气入口)转化为随曲轴转角变化的边界条件. 机油在入口处的实际速度为

v=voil-vp,

(4)

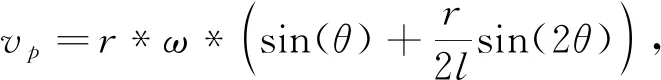
(5)

式中：v为机油在喷嘴处的出口速度，即机油实际相对速度；voil为机油在喷口处的喷射速度；r为曲柄半径；l为连杆长度；vp为活塞瞬时速度；ω为活塞曲轴角速度；θ为曲轴转角，θ=ωt，t为运动时间. 则在标定工况下，机油入口处的机油相对瞬时速度分布如图 1 所示.

图 1 标定工况下的机油瞬时速度Fig.1 Instantaneous speed of oil calibration conditions

2 仿真模型的建立

2.1 几何及网格模型

本文以某高强化柴油机的活塞冷却油腔为分析原型，其具体参数如表 1 所示. 活塞模型如图 2 所示，机油由喷嘴喷出，经油腔入口进入冷却油腔进行周向振荡运动，最终由油腔出口流回到曲轴箱. 本文分别建立了如图 3 所示的水滴形、 椭圆形和卵形3种常见截面形状的冷却油腔，为保证油腔面积不会对振荡冷却效果产生影响，在建模时保证3种油腔的截面积相同，由于冷却油腔结构相对规则，因此采用六面体网格进行模型的网格划分，并对近壁处的网格细化且设置边界层，冷却油腔计算模型如图 4 所示.

表 1 发动机主要技术参数Tab.1 Main technical parameters of the engine

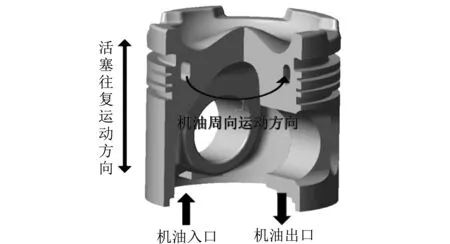
图 2 活塞模型及振荡冷却示意图Fig.2 Piston model and oscillation cooling schematic diagram

图 3 冷却油腔及截面形状Fig.3 Cooling oil chamber and cross-sectional shape

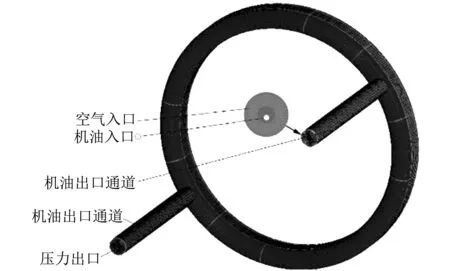
图 4 冷却油腔计算域模型Fig.4 Calculation domain model of cooling oil chamber

2.2 边界条件

使用相对位移法对活塞振荡冷却进行模拟计算时，需要将整个流体域视为刚体运动，将机油入口边界条件转变为随曲轴转角变化的边界条件.

在进行数值模拟时，空气入口处与曲轴箱相通，采用压力入口边界条件，其值为相对静压； 机油入口采用速度入口的边界条件，机油喷嘴出口流量与入口速度的换算公式如下

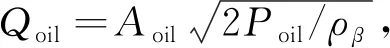
(6)

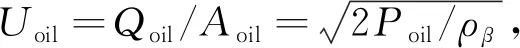
(7)

式中：Qoil为机油流量；Aoil为机油喷嘴出口面积；ρβ为机油密度.

由于冷却油腔出口与曲轴箱相连通，因此假设曲轴箱内部的气压几乎不变，采用压力出口条件，其值为标准大气压.

冷却油腔的壁面边界条件，首先通过Bush提出的管流换热经验公式获得冷却油腔的壁面传热系数[12]，内冷油腔的壁面温度采用文献[8]所提出的壁面边界条件，将内冷油腔的壁面分为如图 5 所示的4个区，各区的壁面温度如表 2 所示.

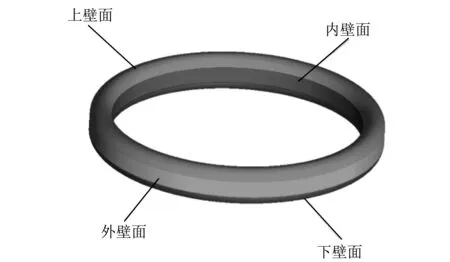
图 5 冷却油腔壁面分区图Fig.5 Cooling oil chamber wall surface partition

表 2冷却油腔壁面边界条件

Tab.2Cooling oil chamber wall boundary condition

壁面名称上壁面内壁面外壁面下壁面温度/K553533498476

2.3 初始化及求解

初始时刻，假设流体域内充满空气，因此设定机油的体积分数为0，且流体域内所有节点速度为0，当相邻两个发动机循环的各个曲轴转角下对应的冷却油腔壁面换热系数和机油填充率的数值相差不超过5%时，即可认为计算收敛.

3 计算结果分析

以该机型的怠速工况作为初始条件，采用SSTk-ω湍流模型进行求解，压力速度耦合采用PISO算法，同时计算了连续性方程、 能量方程和湍流方程.

3.1 截面形状对振荡冷却机油流动特性和机油填充率的影响

图 6 显示了3种不同截面形状的冷却油腔在发动机转速为2 200 r/min时，半个循环周期内不同曲轴转角下的壁面机油分布状态. 通过观察可知，在活塞下行加速时，油腔内大部分机油聚集在油腔顶部，且几乎没有机油流出； 在下行减速过程中，由于活塞速度降低，部分机油从顶部经过侧壁面流下，由机油入口和出口流出； 在上行加速过程中，随着活塞速度的增加，机油聚集在油腔下壁面，且随着曲轴转角的增加而增加； 而在上行减速过程中，机油仍保持一定的惯性，随着活塞速度的减小，部分机油脱离油腔下壁面向油腔顶部运动.

图 6 不同截面形状内冷油腔壁面机油分布Fig.6 Oil distribution in the wall of cooling oil chambers with different shapes

对比3种不同截面形状的冷却油腔壁面机油分布情况可知： 在活塞下行加速过程中，椭圆形和卵形油腔顶部的机油聚集量要远大于水滴形油腔，而在活塞下行减速过程中，水滴形油腔由顶部沿壁面流下的机油量大于其他两种油腔，这是由于椭圆形油腔和卵形油腔的顶部体积大于水滴形油腔，较大的顶部体积有利于油腔在下行过程中顶部机油的聚集； 在活塞上行加速过程中，水滴形油腔底部的机油聚集量要多于其他两种油腔，而在上行减速过程中，水滴形油腔的侧壁面和卵形油腔的外壁面因惯性作用分布的机油较多，这是由于水滴形油腔和卵形油腔的底部体积较大，在活塞上行过程中能在底部聚集更多的机油，同时，倾斜的侧壁面更有利于机油在上行过程中到达油腔的侧壁面.

图 7 为发动机转速为2 200 r/min，3种不同截面形状的内冷油腔机油填充率随曲轴转角的变化情况. 3种油腔的机油填充率变化趋势相似，且填充率在30%～60%的范围内. 活塞在下行加速过程中，由于活塞与机油入口的相对速度不断增加，进入冷却油腔的机油不断增加，当进入下行减速过程中时，一部分上壁面的机油由于惯性脱离上壁面流出油腔，致使油腔机油填充率在150 ℃A 前后达到最大值； 而在活塞上行加速过程中时，由于活塞与机油入口的相对速度不断增加，冷却油腔的内部机油量在不断流失，当进入活塞上行减速过程中时，更多的机油由于惯性作用脱离油腔上壁面向上运动，减小了机油的流失，在330 ℃A前后机油填充率达到最小值.

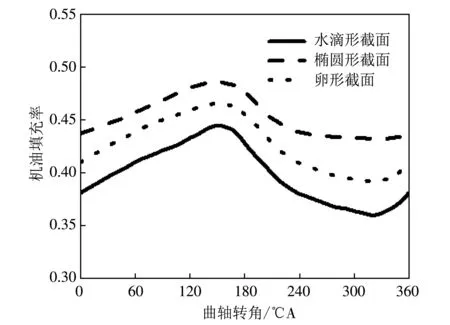
图 7 不同截面形状的油腔机油填充率Fig.7 Oil filling rates of different shapes of oil chamber

通过对比可知，椭圆形油腔的机油填充率最大，水滴形油腔的机油填充率最小，而水滴形油腔的填充率变化幅度要大于其他两种油腔，这是由于水滴形油腔的顶部空间较小，在活塞下行过程中无法在上壁面聚集更多的机油，同时在上行过程中，倾斜的侧壁面对上行的机油有一定的减速作用，进一步加大了机油的流失，降低了机油填充率.

3.2 不同截面油腔振荡冷却的换热特性对比

图 8 为发动机转速为2 200 r/min时，3种形状的内冷油腔壁面平均换热系数随曲轴转角的变化情况.

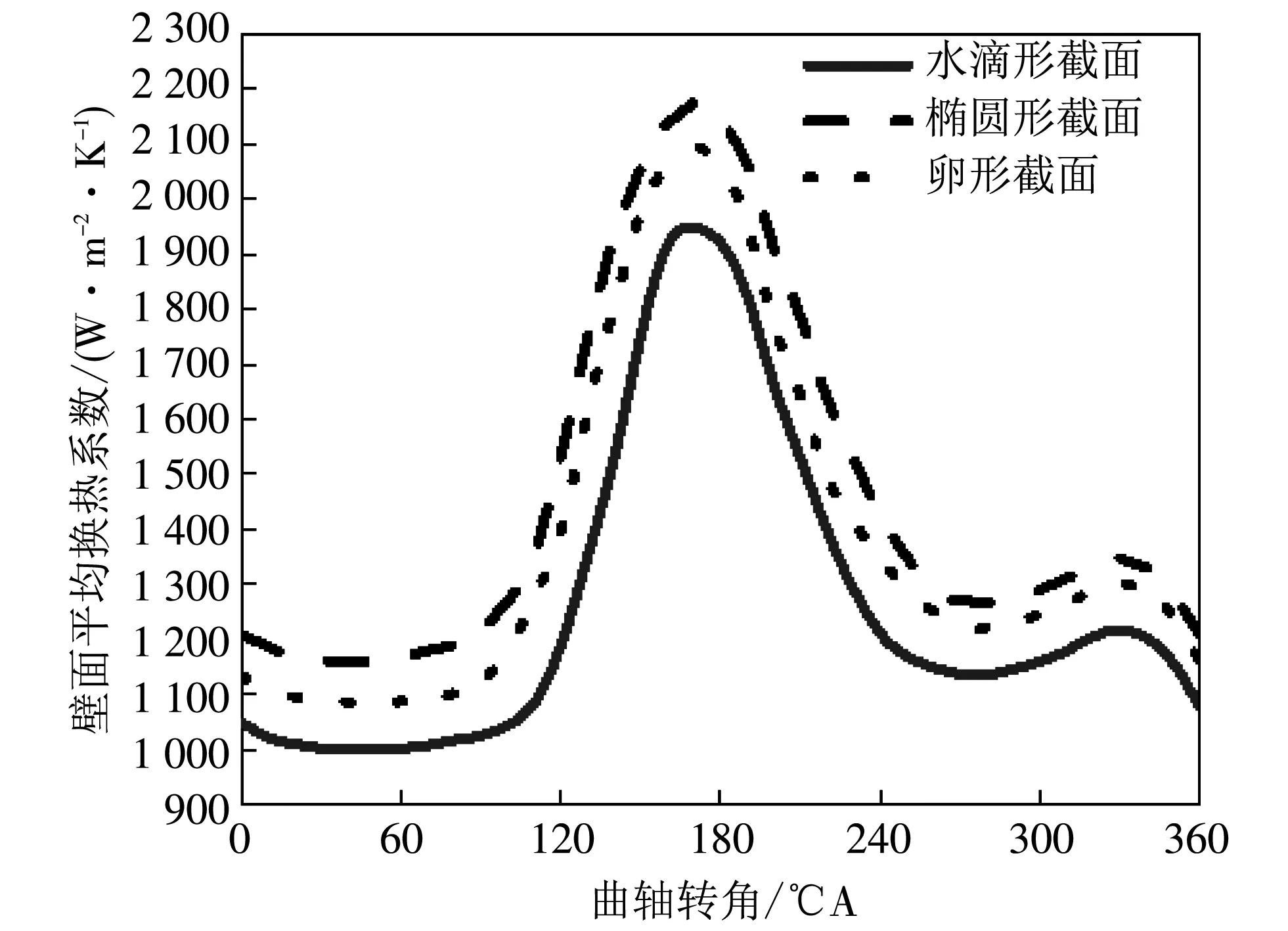
图 8 不同截面形状冷却油腔壁面平均换热系数Fig.8 Average heat transfer coefficient of wall of different cooling oil chamber shape

由图 8 可知，3种油腔的壁面平均换热系数随曲轴转角变化都呈现先增加后减少的趋势，与上文中油腔机油填充率的变化趋势相近，但相对滞后. 其中椭圆形油腔的平均壁面换热系数最高，而水滴形油腔的壁面平均换热系数最低： 由 3种油腔机油填充率的变化可知，椭圆形油腔和卵形油腔的机油填充率相对于水滴形油腔有明显优势，而由于水滴形冷却油腔的顶部空间较小，因此其在活塞下行阶段与另外两种油腔的换热差距要大于在活塞上行阶段的差距，且在下止点前达到最大.

图 9 为3种截面形状的冷却油腔各壁面瞬时平均换热系数随曲轴转角变化的情况. 不同形状的油腔的相同壁面平均换热系数随曲轴转角的变化趋势基本一致，其中上壁面和下壁面由于活塞往复运动而造成的振荡作用，使上壁面和下壁面的湍流混合加强，其壁面换热系数的变化幅度远大于内壁面和外壁面. 通过对比可知，油腔上壁面和下壁面的平均换热系数均是椭圆形油腔最高，水滴形油腔最低； 而对于油腔内壁面的换热系数，水滴形油腔要明显高于其他两种油腔； 对于油腔外壁面的换热系数，卵形油腔最高，且与水滴形油腔相近，大于椭圆形油腔的上壁面换热系数，这是由于侧壁面的倾斜加大了机油与侧壁面的接触，从而提高了侧壁面的换热能力.

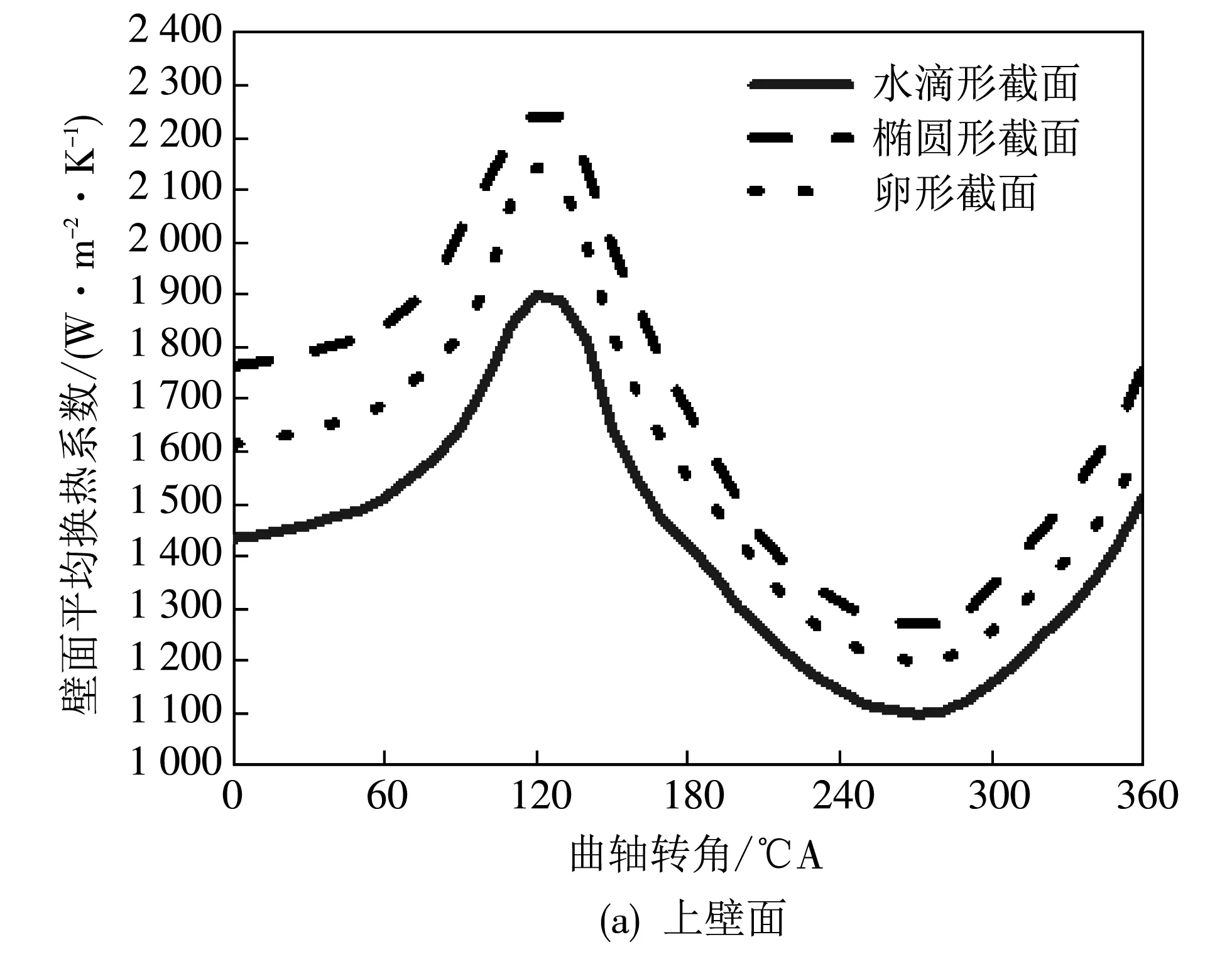
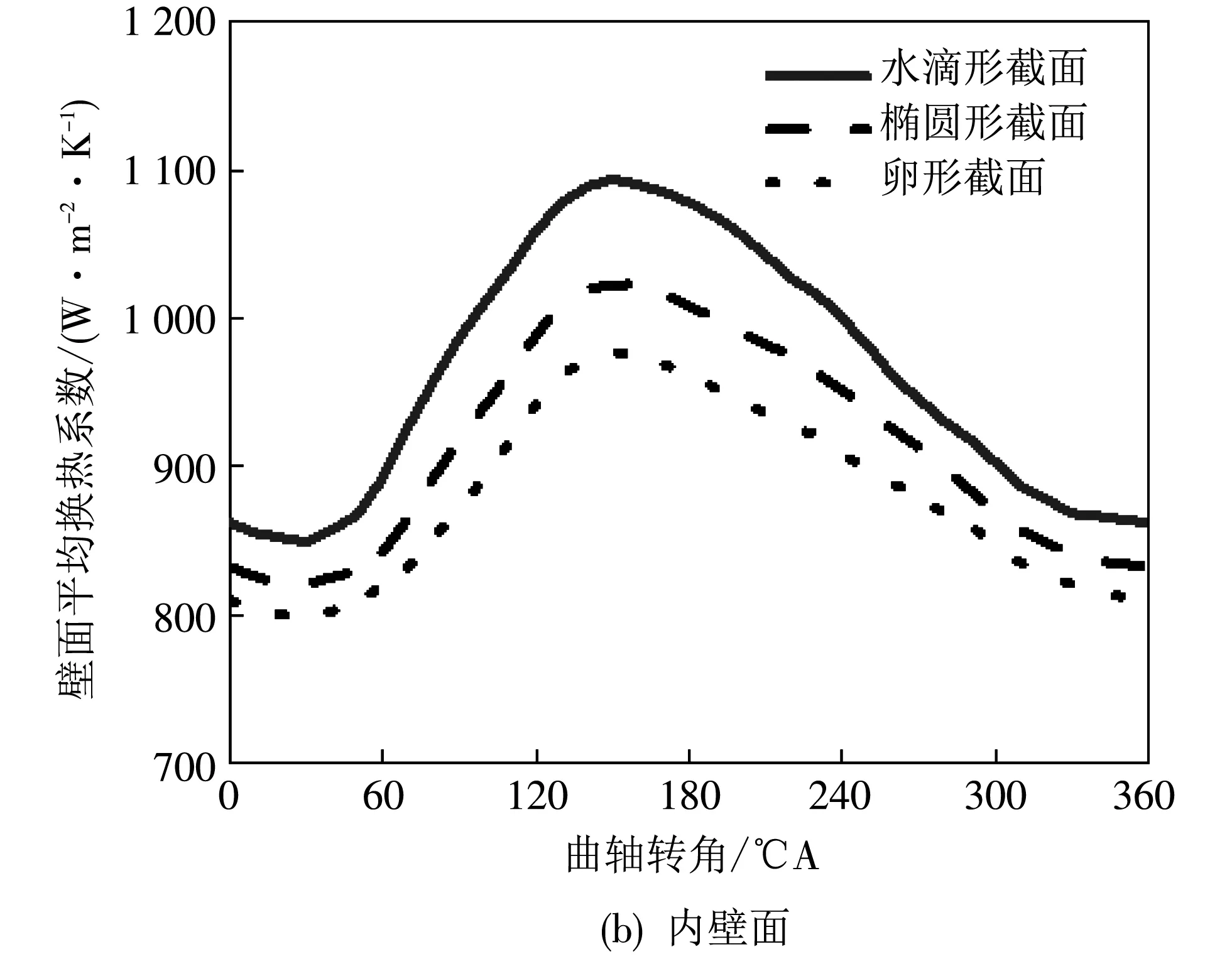
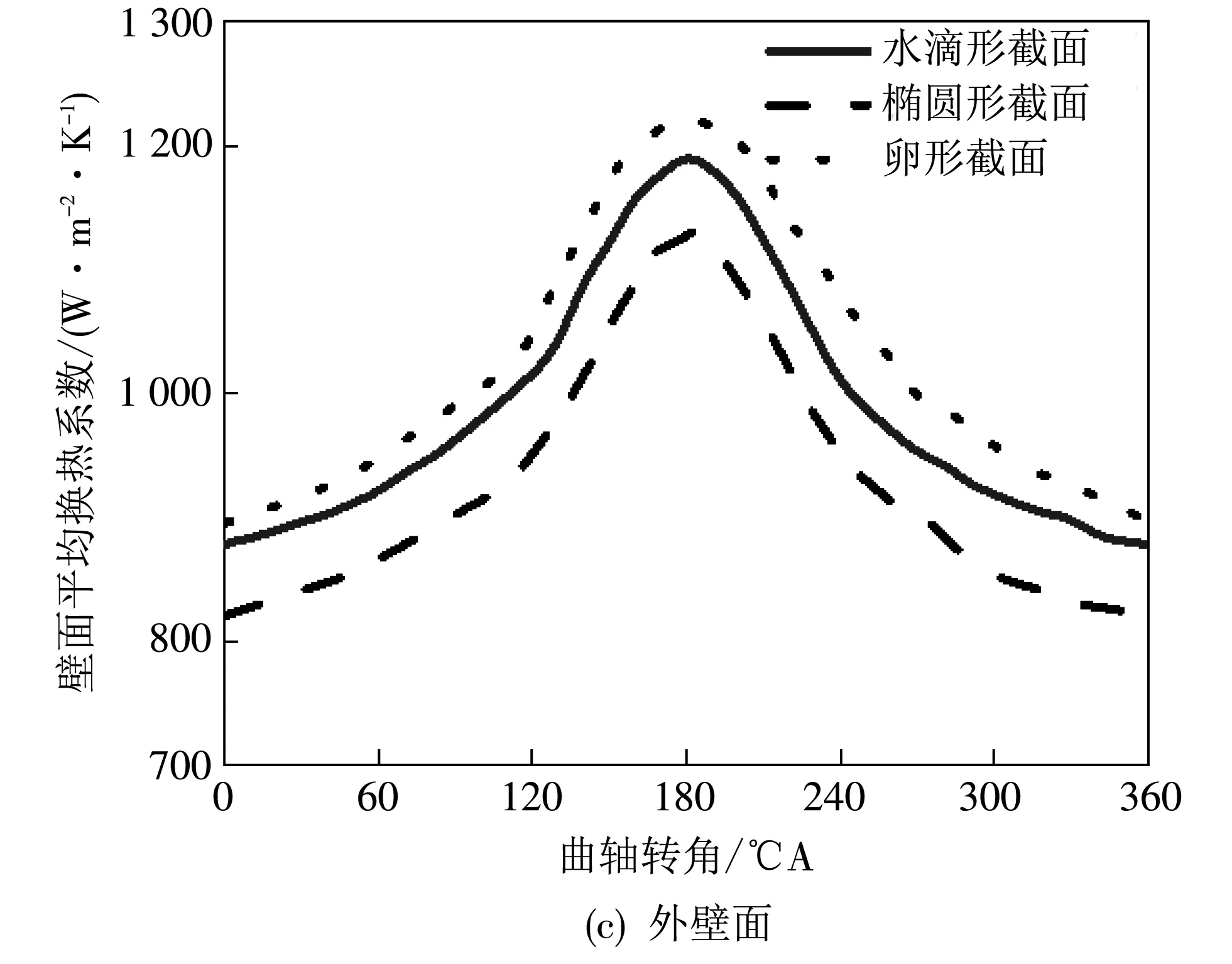
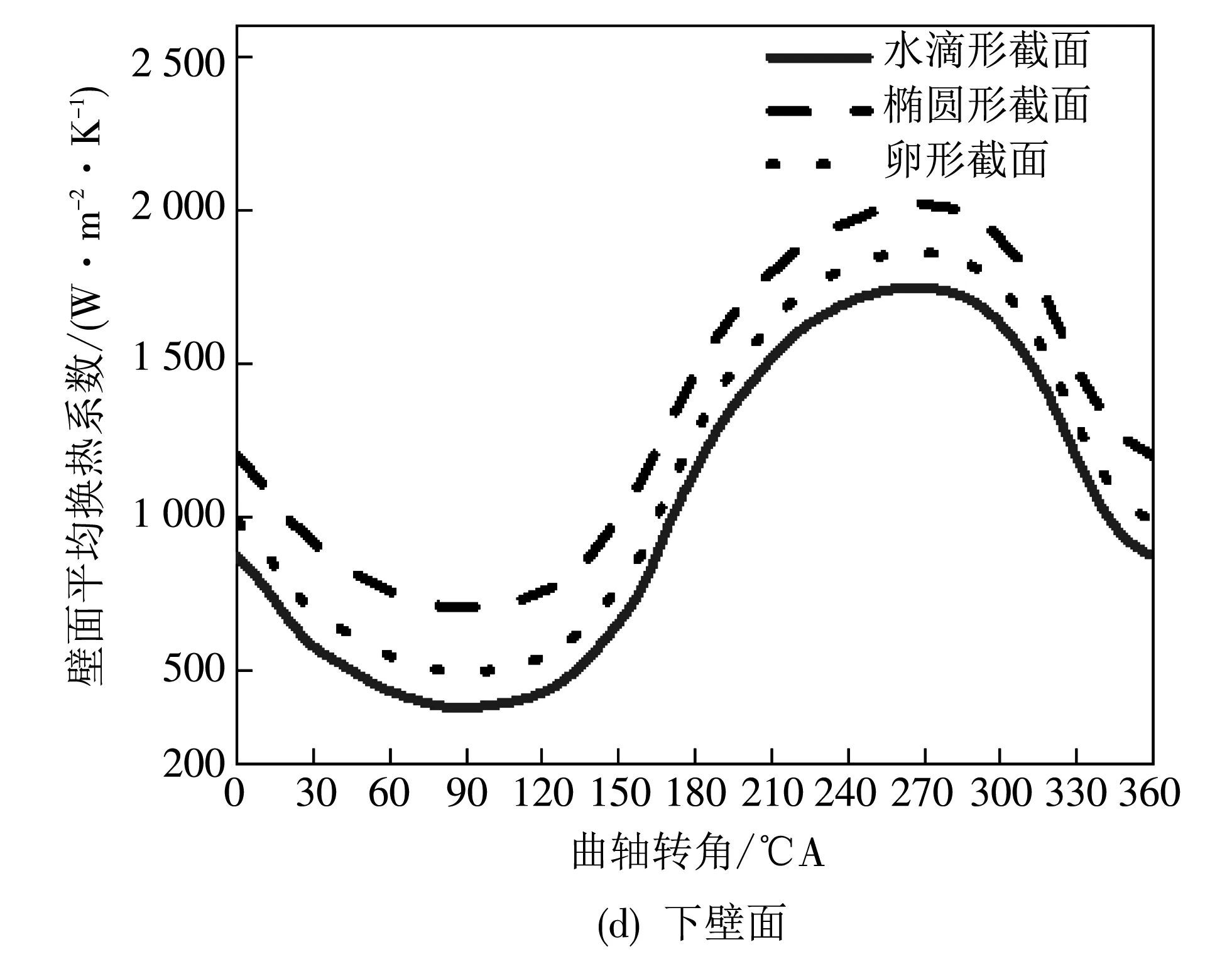
图 9 不同截面形状冷却油腔壁面平均换热系数

3.3 不同转速下不同截面油腔振荡冷却的换热特性对比

为分析不同转速下3种油腔的振荡冷却换热效果，本文计算了发动机转速在1 400～3 000 r/min之间的振荡冷却算例，每隔 400 r/min 取一个算例计算并记录，壁面换热系数随转速的变化情况如图 10 所示.

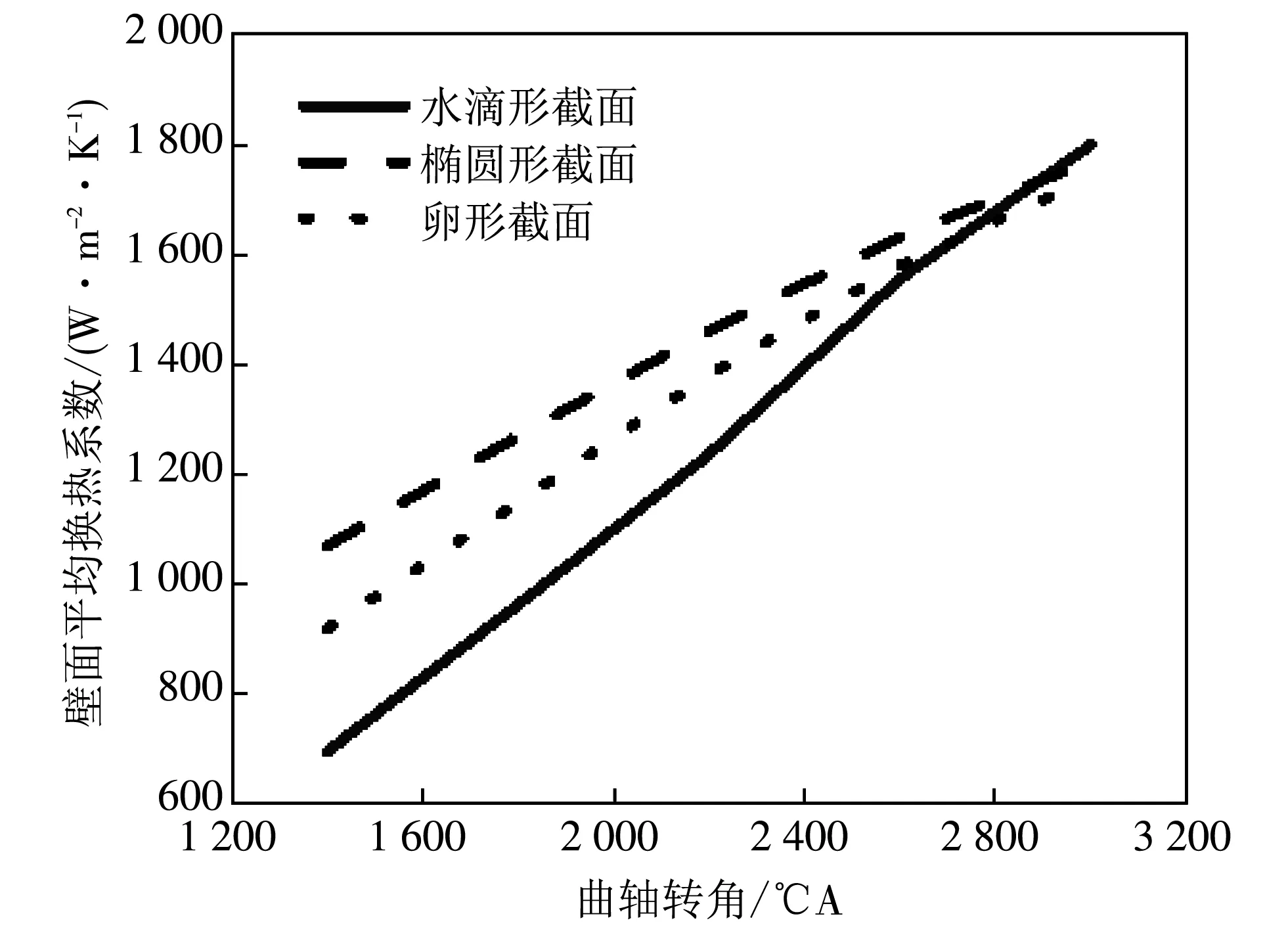
图 10 不同截面形状冷却油腔壁面在不同转速下的平均换热系数Fig.10 Average heat transfer coefficient of different cooling oil chamber shape wall at different speeds

由图 10 可以看出，不同截面形状的冷却油腔平均换热系数都是随转速增大而增大的，在额定转速前，椭圆形油腔的平均换热系数是要高于水滴形油腔和卵形油腔，但随着转速的提高，3种油腔的平均换热系数差别越来越小，并且水滴形油腔在曲轴转速为 2 800 r/min后成为换热性能最好的油腔. 由此可见，在中低转速时，椭圆形油腔的换热性能最好，但在高转速时，水滴形油腔的换热性能最好，这是由于随着发动机转速的提高，3种截面形状油腔的机油填充率差别在不断减小，此时水滴形油腔的细长空间可以更好地形成紊流，从而体现出更强的换热性能.

4 结 论

1) 对比3种油腔在2 200 r/min转速下的机油填充率随曲轴转角的变化情况可知，椭圆形油腔的机油填充率最大，而水滴形油腔的机油填充率最小，且水滴形油腔的机油填充率在整个周期内的变化是最大的.

2) 对比3种油腔各壁面在2 200 r/min转速下平均换热系数随曲轴转角的变化情况可知，椭圆形油腔的换热性能最好，水滴形油腔的换热性能最差，但是水滴形油腔的侧壁换热性能要强于其他两种油腔，一定程度的倾斜有利于冷却油腔侧壁的换热.

3) 对比3种油腔在不同转速下的平均换热系数可以得出，在中低转速下，由于椭圆形油腔的机油填充率明显高于其他两种油腔，其换热性能有明显的优势； 而在高转速下，在机油填充差距不明显的情况下，水滴形油腔由于其狭长的形状能更好地形成紊流，其换热性能优势明显.