装盒机成品输出机构关键参数设计与分析

刘 滨，刘建春，刘智超，范 达

（锦州万得包装机械有限公司，辽宁锦州 121000）

0 引言

盒包装具有加工成本低、储运方便以及适用于各种印刷方式的特点，广泛应用于食品、药品等行业［1-2］。全自动装盒机集机、光、电、气于一体，除了向盒坯料仓内放置盒坯外，其余工序如取盒、开盒、放盒、产品入盒、字码压印、关舌、封盒、输出等操作均由机器完成［3-4］。目前，国内的全自动装盒机与国外相比，在技术方面还有一定的差距［5-6］，对于装盒机的研究多集中在取盒和开盒成型机构［7-12］，还未见关于装盒机成品输出机构的报道。成品输出机构作为装盒机的最终输出端口，主要用于承接由纸盒输送链传递过来的关闭完好的成品纸盒，并向下游设备输出。对于成品输出机构的设计，过去通常依据经验以及试验结果，缺少理论计算分析。本文在分析成品由输盒链过渡到输出机构过程中输盒链夹指和纸盒运动规律的基础上，研究输出机构的横向位置eb和速比ivbc这2个关键参数对包装盒与夹指间距变化规律的影响。

1 包装盒成品输出过程分析

在目前应用最多的卧式装盒机中，纸盒传送装置通常采用输送链的形式。打开成型的纸盒在纸盒输送链上夹指的夹持下做水平方向的直线运动，依次完成被包装物入盒、关小舌、压印、关大舌后，传送至位于输送链末端的成品输出机构。图1为某型全自动装盒机的主要部件一览图。

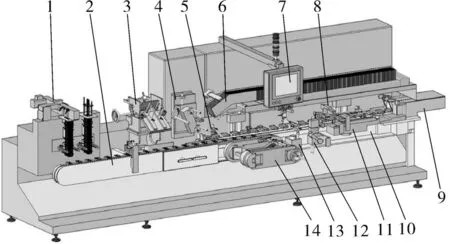
图1 装盒机的主要部件一览图Fig.1 Overall structure diagram of main functions of cartoning machine

图2 输盒链结构示意图Fig.2 Schematic diagram of the structure of the carton conveying chain

在纸盒输送链的链节上，按一定的节距间隔安装夹指，纸盒被位于其两侧的夹指约束，并随之运动，如图 2所示。在纸盒四角处共有4个夹指限位，保证纸盒准确可靠定位。为适应不同宽度和长度的纸盒，夹持夹指在纸盒宽度和长度方向的间距均可调。4个夹指分别安装在各自的滚子链上，由对应的链轮驱动。在纸盒长度方向上，将外侧的夹指固定，作为定位基准，里侧夹指可调，即链轮3，4一同沿轴向移动，带动里侧的滚子链和夹指改变位置，以适应不同长度的纸盒。在纸盒宽度方向上，将左侧夹指固定，作为定位基准，右夹指可调，故在驱动机构中设有离合器，在需要调整夹指间距时将离合器脱开，盘动链轮1，4改变右侧夹指位置，调整完毕后再将离合器接合锁紧。4条输盒链并排同心布置，由同一根花键轴驱动。正常工作时，离合器处于闭合状态，这4条输盒链保持同步运动。

纸盒被夹指夹持，随输送链水平移送，进入成品输出机构，随即被1对竖直安装的输出输送带夹持，输送至下一个工位，过程如图3所示。其中，w为纸盒宽度；h为纸盒高度；c1为纸盒右边沿下顶点；c2为纸盒左边沿下顶点；p1为右侧夹指右边沿与纸盒底边轨迹的交点；p2为左侧夹指右边沿上顶点；rsp为链轮的平均半径；rbottom为链轮中心至纸盒底边的距离；rtip为链轮中心至夹持夹指顶点的距离；eb为带轮轴心与链轮轴心的横向距离。

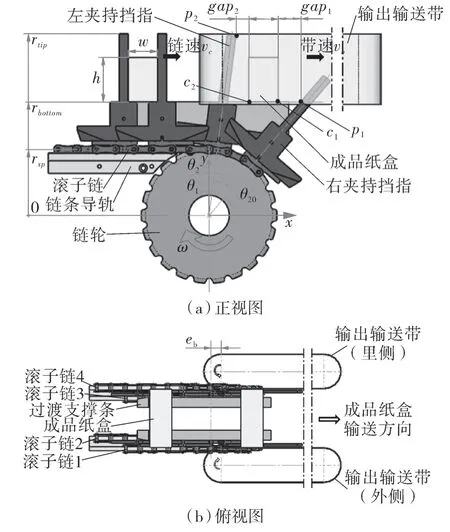
图3 包装盒成品由纸盒输送机构过渡到输出机构的过程Fig.3 The process of transition of the finished packaging box from the carton conveying mechanism to the output mechanism

夹指固定在链节上，随滚子链节一起运动。在纸盒输送链的水平段设置有上下导轨，对滚子链进行支撑和限位，防止夹指发生倾斜，保证纸盒向右运动过程中姿态稳定。在纸盒输送链的尾端，链节将逐渐脱离导轨并与驱动链轮啮合，之后便随链轮一起做圆周运动，这个过程中，固定在链节上的夹指也随链节一同由水平运动过渡到绕链轮中心的圆周运动。

在水平段，纸盒随夹指一同水平向右匀速运动。运动到纸盒输送链的尾端，右侧夹指转变为圆周转动后，因其切向线速度增大，将逐渐远离其所夹持的纸盒，且夹指因转动而向前倾斜，直至完全退出纸盒的输送路径。在接触输出输送带之前，纸盒在左侧夹指推动下随之一同以链速vc水平向右匀速运动。当纸盒运动至内外输出输送带之间时，便被这2条输送带夹紧并随之以带速vb向后输送，直至从输送带上落下，完全脱离装盒机。

在包装盒成品由输盒链过渡到输出机构过程中，纸盒与其两侧的夹指的间距实时变化。有2个参数直接影响纸盒与其两侧夹指间距的变化，一是输出输送带与纸盒输送链的相对位置，即在纸盒运行方向上，输出输送带的带轮轴心与纸盒输送链的链轮轴心的距离eb；二是输出输送带的带速vb与纸盒输送链的链速vc之速比ivbc。前者决定纸盒与输出输送带发生接触的时间，即开始增速输出的早晚，后者则确定纸盒的输送速度，这2个参数若取值不合理，则可能导致纸盒与夹指发生干涉。

2 纸盒与夹指的间距变化规律

2.1 夹指的运动规律

尽管链传动存在多边形效应，其瞬时链速和瞬时传动比不是常数，但由于能保持准确的平均链速和平均传动比，且运行转速较低，故不会对纸盒输送链的正常工作造成明显影响。为简化分析和计算，假定链节以平均链速匀速运行。设链轮的节距为p，齿数为z，则链轮的平均半径：

设链轮转速为ω，则在水平段，夹指的速度即输送链的平均链速：

当夹指所在的链节与链轮发生接触并逐步完全啮合后，夹指便随链轮以角速度ω转动。以链轮中心O点为原点，建立平面坐标系xOy，如图4所示。设右侧夹指所在链节与链轮刚接触时（即链节右侧滚子进入链轮齿槽的中心时）为起始时刻，则右侧夹指和其所在链条的驱动链轮相对于各自起始位置的转角分别为θ1和θ2。

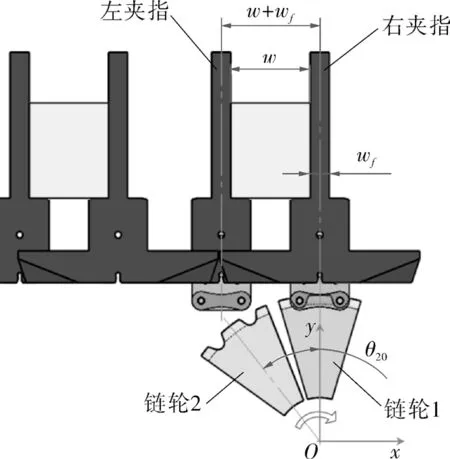
图4 起始时刻夹指的位置Fig.4 The position of the clamping finger at the starting moment

设夹指宽度为wf，则水平段两侧夹指的间距为w+wf，由运动关系可知，两侧夹指所在链轮的转角差值：

即左侧夹指相对于右侧夹指角度落后θ20，左侧夹指所在链轮2的转角：

2.2 纸盒的运动规律

在水平段，纸盒接触输出输送带之前，随夹指一同水平向右匀速运动，其速度为输送链的平均链速vc。

当纸盒运动至内外输出输送带之间时，便被这2条输送带从纸盒长度方向上夹紧，并随之以带度vb向后输送。为简化传动机构，常将输出输送带与纸盒输送链设计成共用同一根驱动轴作为动力输入，所以vb和vc成比例关系。设此驱动轴至输出输送带带轮的传动比为ib，带轮半径为rb，则带速：

可进一步变换为：

其中，ivbc=rb/（rspib），即vb和vc之比。在进入输出输送带之前，纸盒以速度vc水平向右匀速运动。纸盒质量较轻，且内外侧输送带能给纸盒足够大的夹紧力和摩擦力，认为纸盒在与输送带最先接触于两者的切点处时，速度瞬间与之达到同步，即vc瞬间变化为vb，纸盒的输送速度随位移的变化规律：

其中，xc1为纸盒右边缘的横坐标；eb为输出输送带带轮中心的横坐标。

纸盒由初始位置运动到刚与输出输送带接触时，链轮转过角度：

纸盒右边缘横坐标：

因此左边缘横坐标：

2.3 纸盒与夹指的间距变化规律

（1）右侧间距gap1，即纸盒右边缘与其右侧夹指的间距。

夹指为圆周运动，则夹指上最靠后的位置为图3中P1点，由几何关系可计算出其横坐标：

于是可得右侧间距：

（2）左侧间距gap2，即纸盒左边缘与其左侧夹指的间距。

左侧夹指与链轮进入啮合后，便由水平运动变为转动。夹指右顶点P2的水平坐标：

为简化问题，左侧夹指与纸盒的最小距离可用其右顶点与纸盒左连缘的距离近似表示，即

经初步设计，已经确定相关变量的数值为p=25.4 mm，z=22，rsp=88.9 mm，rb=30.0 mm，wf=12.0 mm，rbottom=154.0 mm，rtip=246.0 mm。在此基础上，取eb=20 mm，ivbc=2.5，w=40 mm时，点P1，P2，C1，C2的水平坐标以及gap1，gap2随链轮1转角的变化曲线分别如图5，6所示。

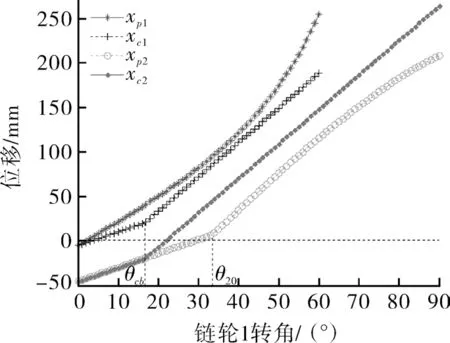
图5 点p1，p2，c1，c2水平坐标的变化Fig.5 Change of horizontal coordinates of points p1，p2，c1，c2

图5中，xp1为1条平滑曲线；xc1和xc2均由2段直线构成，纸盒在链轮转角为θcb时接触输送带，速度从vc突变为vb；xp2由2段直线构成，在链轮转角为θ20时，左侧夹指由水平段转变为圆周段。

图6中，gap1的曲线由2段构成，第1段为0＜θ1＜θcb时，纸盒还未接触输送带，gap1匀速单调增大；第2段为θcb＜θ1时，纸盒接触输送带后以带速vb运动，gap1先减小后增大。根据几何关系，当θ1＞60°时，右侧夹指已完全退出纸盒的行径范围，不会发生干涉，故不再绘出。gap2的曲线由3段构成，第一段同样为0＜θ1＜θcb时，左侧夹指位于水平段以链速vc向右运动，且纸盒还未接触输送带，纸盒与左侧夹指保持接触呈相对静止状态，故gap2=0；第二段为θcb＜θ1＜θ20时，左侧夹指仍位于水平段以链速vc向右运动，但纸盒接触输送带后以带速vb运动，gap2单调增大，增大速率即速度差vb-vc；第三段为θ20＜θ1时，左侧夹指由水平段转变为圆周段，因此gap2先减小后增大，同样根据几何关系，当θ1＞90°时，左侧夹指已完全退出纸盒的行径范围，故不再绘出。

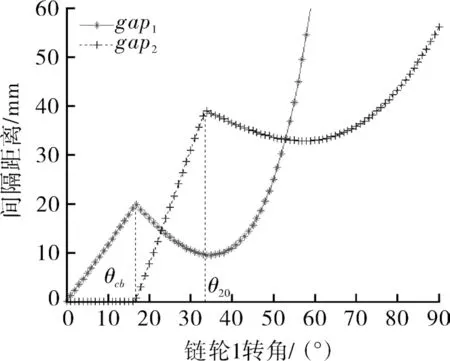
图6 gap1和gap2的变化（eb=20 mm，ivbc=2.5）Fig.6 Change of gap1 and gap2 （eb=20 mm，ivbc=2.5）

根据式（12）（14）可知，gap1与纸盒宽度w大小无关，而gap2则随w的增大而增大。说明纸盒越宽，其左侧越不容易发生干涉。故以最不利的情况为例进行分析，即纸盒宽度取最小值w=30 mm时，不发生干涉，则当w＞30 mm时，将更安全。

3 eb和ivbc的取值

观察过渡过程中gap1和gap2的数值变化，可发现gap1在θ1＞θcb之后，以及gap2在θ1＞θ20之后，均有先减小后增大的特性，因此计算此过程中gap1，gap2的极小值gap1min，gap2min，以此作为评价值研究eb和ivbc的影响。

初步计算可确定eb和ivbc的取值范围分别为-5～40 mm和1.5～4，进一步遍历该范围内两者的一系列取值组合，计算出对应的gap1min和gap2min，并作三维曲面图如图7，8所示。

图7 gap1min的三维曲面图Fig.7 3D surface plot of gap1min

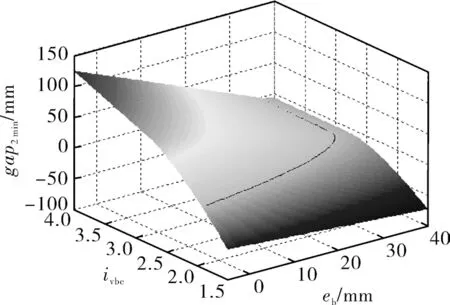
图8 gap2min的三维曲面图Fig.8 3D surface plot of gap2min

当eb增大时，gap1min随之增大，而gap2min随之减小；当ivbc增大时，gap1min随之减小，而gap2min随之增大，说明eb，ivbc对gap1，gap2的影响完全相反。

图7，8中的黑色交线分别代表gap1min=0和gap2min=0，位于该交线上方的区域才不会发生干涉。若要求纸盒左右两侧均不发生干涉，eb和ivbc应选在两曲面各自交线上方重叠的区域内。

为更直观地同时观察gap1min和gap2min，作等高线图如图9所示，gap1min=0和gap2min=0对应的2条等高曲线所围区域即eb和ivbc可选的范围［13-14］。

图9 gap1min和gap2min的等高线图Fig.9 Contour diagram of gap1min and gap2min

在确定eb，ivbc，gap1min，gap2min参数中任意2个的大小后，即可用图9确定另外2个的数值。

从安全的角度，应使整个过渡过程中gap1，gap2的最小值尽量大，若两处的安全距离同等重要，则要求gap1min=gap2min。此时，eb=26.8 mm，ivbc=2.7，对应图9中A点。gap1，gap2的变化规律如图10所示，两者同时到达15.0 mm，此为gap1min，gap2min所能同时达到的最大值。

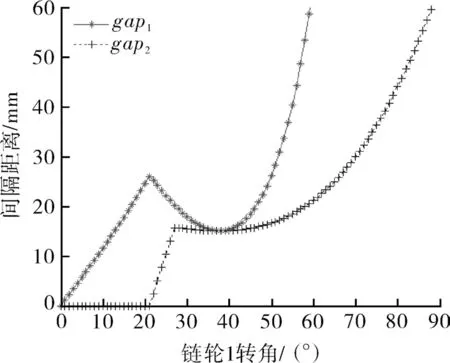
图10 gap1和gap2的变化（eb=26.8 mm，ivbc=2.7）Fig.10 Change of gap1 and gap2 （eb=26.8 mm，ivbc=2.7）

若为降低功耗和振动噪声且保证运行平稳，应使输出输送带的带速vb尽量低。根据分析已知ivbc，eb对gap1，gap2的影响相反，因此可以在减小ivbc的同时减小eb，以尽量使ivbc取得最小值。但为保证不发生干涉，gap1min，gap2min的下限均为0，即2处均达到干涉的临界值，ivbc，eb达到最小值，对应于图9中B点，其坐标为eb=-0.5 mm，ivbc=1.9。此时gap1，gap2的变化规律如图11所示，gap1，gap2先后在不同时刻到达0 mm，纸盒左右均处于干涉临界值。

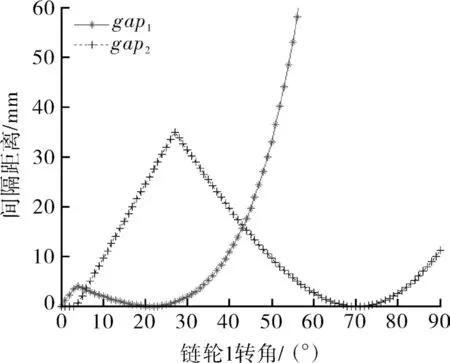
图11 gap1和gap2的变化（eb=-0.5 mm，ivbc=1.9）Fig.11 Change of gap1 and gap2 （eb=-0.5 mm，ivbc=1.9）

实际设计中还应结合具体情况进行分析，使各参数取值合理。以某型装盒机为例，最终确定eb=20 mm，ivbc=2.3，对应图9中C点，此时gap1min=14.5 mm，gap2min=5.5 mm。

经过样机的实际试验，测量结果见表1，实测值与理论计算值基本一致，达到预期要求。

表1 gap1min 和gap2min的实测结果Tab.1 Measured results of gap1min and gap2min mm

最终的成品输出机构如图12所示。

图12 装盒机的成品输出机构Fig.12 Finished product output mechanism of the cartoning machine

4 结语

在装盒机中纸盒由输盒链过渡到输出机构过程中，通过对输盒链夹指和纸盒的运动分析，得出包装盒成品与其两侧夹指间距的变化规律，以水平位置eb和速比ivbc这2个关键参数为设计变量，分析其对间距的影响。在确定eb，ivbc，gap1min，gap2min参数中任意2个的大小，就可以利用计算得出的过渡过程中两侧间距极小值的等高线图，确定另外2个的数值，极大方便于参数的设计。实际样机试验，验证了方法的正确性。研究为装盒机中成品输出机构设计提供理论依据。