焊接结构随机振动疲劳分析方法研究与应用

周晓坤,裴宪军,董平沙,贺茂盛,谢素明,付婷婷

(1.大连交通大学 机械工程学院,辽宁 大连 116028;2.中车齐齐哈尔车辆有限公司大连研发中心,辽宁 大连 116052;3.东南大学 机械工程学院,江苏 南京 211189;4.密歇根大学 船舶与海洋工程学院,美国 安阿伯市 48109;5.北京交通大学 机械与电子控制工程学院,北京 100044;6.中车齐车集团有限公司货车研究院,辽宁 大连 116052)

0 引言

振动疲劳是机械产品在正常服役过程中最易发生破坏的模式。轨道车辆运行过程中,车体结构往往因道路颠簸、动力系统运行而受到不同频率的外部激励,当外部激励的频率与车体结构固有频率接近时,车体结构会发生疲劳破坏,传统的基于单轴静载荷的疲劳分析方法会因忽略共振效果低估车体的疲劳损伤[1],导致结构发生疲劳破坏。

随机振动疲劳分析既可以在时域进行,也可以在频域进行。在时域分析中,通过有限元动态分析得到应力历程,然后应用循环计数程序计算累积疲劳损伤[2],白春玉等[3]研究了多轴应力响应下结构振动疲劳寿命预估的时域方法,赖韬[4]研究了线弹性结构时域动态荷载识别方法。然而,当处理复杂结构时,由于计算成本极高[5],这些方法很难应用于工程研究。在频域分析中,可以很容易地通过频响函数(Frequency Response Function,FRF)计算疲劳易发部位的应力谱,频响函数通过估计周期振幅分布来计算疲劳损伤[6]。因此,频域疲劳分析也称为谱疲劳法,其计算效率较高,在结构设计早期阶段应用较多[7-8]。朱涛等[9]用频域法研究了转向架的疲劳寿命;马国茂等[10]基于频域法的随机振动载荷对结构进行疲劳分析;赵霞军等[11]采用频域法对机载电子设备的随机振动进行了疲劳分析;谢敏捷等[12]基于时域法和频域法对车身动态疲劳进行分析;高博等[13]开展了疲劳损伤谱时域、频域计算方法及其等效性验证,证明了疲劳损伤谱的时域算法与频域算法具有等效性。产品设计初期可以用频域法指导方案设计,产品详细设计期可用时域法详细计算单元和焊点损伤。

对于单轴应力主导的疲劳损伤,有几种谱疲劳方法[14-16]可以用线性损伤模型(如Miner’s规则)估计循环振幅分布,进而估计疲劳损伤。BRACCESI等[17-18]对常用的分析谱进行了对比研究,其中Dirlik的方法[19]以及Benasciutti和Tovo谱矩方法[20]被研究和工程界广泛接受。当处理多轴疲劳时,上述方法引入一个等效的单轴应力准则,而且计算采用的应力谱、频域等效von Mises判据在特定点已知[20]。目前多轴疲劳问题虽然已有大量研究,但是绝大多数研究关注材料的时域多轴疲劳问题,比较常见的频域多轴疲劳准则是等效von Mises多轴疲劳判据[20],然而该判据并不能有效反映多轴疲劳非比例应力分量效应,而且鉴于焊接接头疲劳行为的特殊性,目前针对整体焊接接头的多轴疲劳研究相对较少,尤其是焊接接头频域非比例多轴疲劳研究。因此,现有研究缺乏能够有效处理焊接结构非比例多轴疲劳损伤的方法。

由于焊接接头的材料非均质特性、几何不连续性及存在残余应力3个显著特点,焊接接头的设计和分析更加复杂,决定了其疲劳破坏机理的特殊性[21]。

本文提出一个基于路径依赖的最大范围法(Path-Dependent Maximum Range,PDMR)的时域疲劳准则[22]评估焊接结构的多轴随机振动疲劳方法。PDMR多轴疲劳准则是专门针对焊接接头的多轴疲劳准则,可以有效描述多轴应力分量的非比例效应[22]。该方法采用稳健的网格不敏感结构应力方法和模态分解方法来确定焊接接头法向和剪切应力响应,通过小规模数据驱动方法获得刻画非比例应力分量效应的相关函数[22],将法向正应力和剪切应力的功率谱密度(Power Spectral Density,PSD)和与其交叉的功率谱密度(Cross Power Spectral Density,CPSD)相关联,建立频域PDMR应力功率谱,并将某高速货车整车常用速度范围内的振动加速度试验数据作为输入,利用本文提出的随机振动疲劳方法,对160 km快捷货车的关键接头进行疲劳寿命分析。另外,根据各个模态对疲劳的贡献分量,提出车体的疲劳优化改进方案,并对比了改进前后车体关键接头的疲劳寿命。

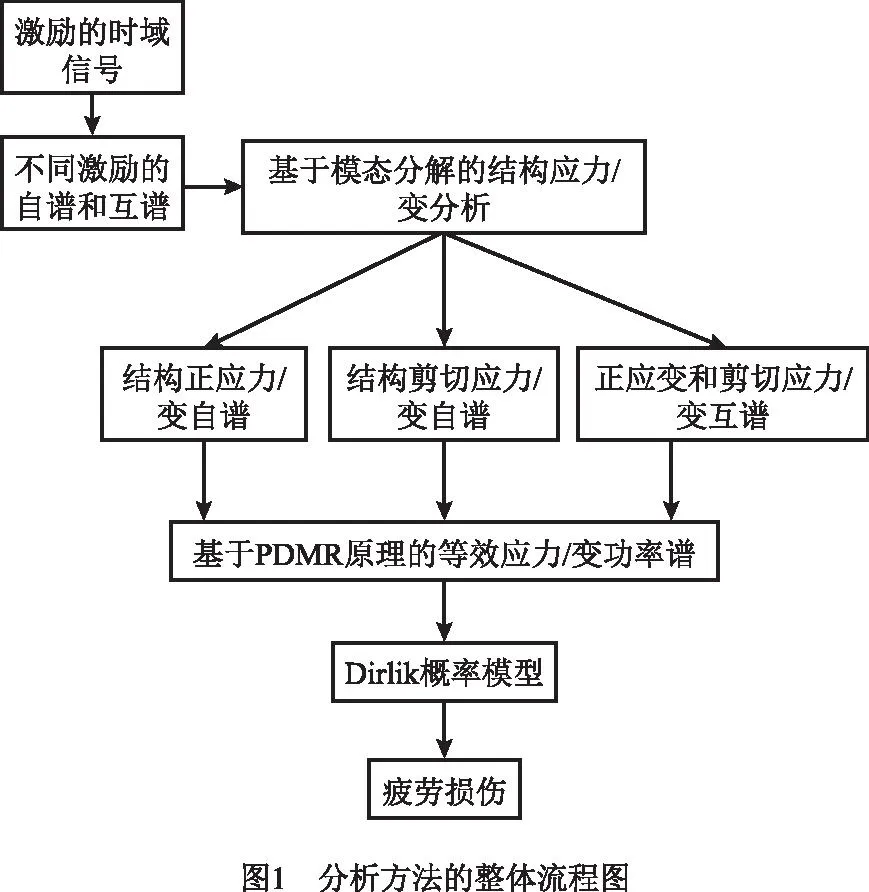
1 基于结构应力的焊接结构随机振动疲劳分析方法

基于模态分解的结构应力频域疲劳分析方法流程如图1所示。对于给定外载荷的时间信号,首先通过快速傅里叶变换及相关操作求得不同激励载荷的自谱和互谱;然后将载荷的自谱互谱作为输入,通过模态分解与结构应力方法得到接头结构应力(包括正应力和剪切应力)的自谱和互谱;再利用各分量结构应力信息,计算得到基于PDMR原理的等效结构应力功率谱;最后通过Dirlik概率模型计算结构的损伤[23]。

1.1 模态结构应力

结构动力学方程的一般形式为

(1)

式中:M,C,K分别为质量、阻尼和刚度矩阵;{u(t)},{f(t)}分别为位移和载荷向量。根据结构系统的各阶固有频率和各阶主振型(模态),利用线性代数理论,可以将向量构成一个维空间的向量基。多个自由度系统时间历程上的位移响应可以表示为该正交主振型的线性组合

(2)

式中:qj(t)为模态坐标;φj为模态振型。基于上述模态叠加概念,对结构关键焊缝处的结构应力进行类似处理。针对每种振型,通过传统结构应力分析方法计算对应振型下关键焊线处结构应力的向量。如果在振型φΨ下,计算得到的焊线处结构正应力和结构剪切应力分别为σφ和τΨ,则利用模态叠加原理[23],焊线处的结构应力为:

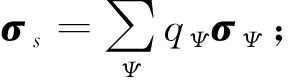
(3)

1.2 结构应力功率谱

对于频率为Ω的简谐激励(向量)f,激励可以写成复数形式

f=eiΩtf*,

(4)

其结构的稳态响应通过下式计算:

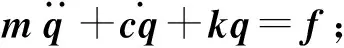
(5)

整理得

-Ω2mq*+icΩq*+kq*=f*。

(6)

求解得到简谐激励下模态坐标的解,其中q*为复数,其模为响应的幅值,幅角为与激励的相差。假定系统质量、阻尼、刚度不随时间变化,系统可简化为线性系统,计算得到结构多点激励位置的频率响应矩阵H(f)。利用傅里叶变化,通过结构多点激励位置的时域激励信号得到激励的输入功率谱矩阵Sxx(f)。结构的模态坐标功率谱矩阵

Sqq(f)=H*(f)Sxx(f)HT(f)。

(7)

式中:H*为频率响应矩阵的共轭;HT为频率响应矩阵的转置。

得到结构模态坐标功率谱矩阵后,计算焊线上第i个节点的功率谱

(8)

式中σi为焊线上第i个节点在不同模态(振型)下的应力向量,即σi为矩阵∑T的第列:

(9)

式中N为系统的总振型数。

结构正应力与结构剪切应力的互谱为

(10)

1.3 基于PDMR的结构应力功率谱

将结构所受的多轴疲劳应力状态分为比例多轴应力和非比例多轴应力。试验表明,非比例多轴应力对结构的疲劳破环比较严重。为更好地描述非比例载荷破坏情况,DONG等[22]提出PDMR方法,基于该方法提出了等效结构应力功率谱概念。

结构所受的剪切结构应力和正应力有固定的比例关系时,可以定义等效结构应力

(11)

对于一般材料,β=3,等效结构应力功率谱的计算公式为

Seq(f)=Φ[Sσσ+βSττ]。

(12)

式中Sσσ,Sττ为结构正应力和结构剪切应力的功率谱,是待定修正参数。结构正应力与结构剪切应力成比例程度较高时,两个应力分量的相关系数ρ趋近于±1;而当两者接近非比例状态时,其相关系数几乎为0。因此,可以用相平面上结构正应力/剪切应力的相关系数ρ表征应力分量之间的成比例关系。式中的Φ可以表达为相关系数ρ的函数Φ(ρ)。

在时域信号中,结构正应力和结构剪切应力的相关系数

(13)

式中:cov(σ,τ)为结构正应力和结构剪切应力的协方差;STD(σ),STD(τ)分别为结构正应力和结构剪切应力的标准差。为了减少计算工作量,推导出等效于时域相关系数ρ′στ的频域相关系数ρστ[23-24],

(14)

关于修正函数Φ(ρ),初步采用小规模数据驱动方式实现:首先在ρ∈(-1,1)范围内等距生成不同的ρk(k=1,2,…,61)。不同的ρk生成100组相同相关系数的信号,每个信号都可以求解出不同的Φi(ρk)(i=1,2,…,100),从而得到6 100组不同的数值。将这些数据进行多项式拟合,得到Φ(ρ)的修正函数表达式,公式对应的系数如表1所示。

表1 式(15)对应的系数

Φ(ρ)=c8ρ8+c7ρ7+c6ρ6+c5ρ5+c4ρ4
+c3ρ3+c2ρ2+c1ρ+c0。

(15)

1.4 疲劳损伤估计

利用式(12)计算获得等效结构应力谱后,通过Dirlik公式求得等效结构应力的概率密度分布函数

(16)

(17)

(18)

(19)

(20)

D3=1-D1-D2。

(21)

(22)

(23)

(24)

式中:Z为归一化幅值,Q为质量因子,R为Dirlik定义的参数;xm为平均频率,m0,m1,m2,m4为功率谱密度函数的第i个矩;γ为最大应力与抗拉强度之比;D1,D2为破坏强度。

相应的疲劳损伤可以通过式(16)和式(18)计算得到。

(25)

式中C,h为主S-N曲线参数。对于给定的时间跨度T,对应的等效结构寿命为

(26)

2 某高速铁路货车随机振动疲劳寿命预测

本章基于整车振动试验台开展整车振动试验,将整车多通道试验台速度激励作为输入,同时完成整车模态和模态结构应力分析,求出频域响应与模态坐标,完成结构应力功率谱和等效结构应力功率谱计算,估计疲劳损伤与寿命[25]。

2.1 车辆结构与载荷试验

2.1.1 车辆结构

该铁路货车运行时速160 km,主要由钢结构车体、活动侧墙、转向架、车钩缓冲装置和制动装置等组成。该车车辆长度为24 136 mm,轴重18 t,自重为38 t,载重为34 t,车辆容积为205 m3。

2.1.2 载荷试验

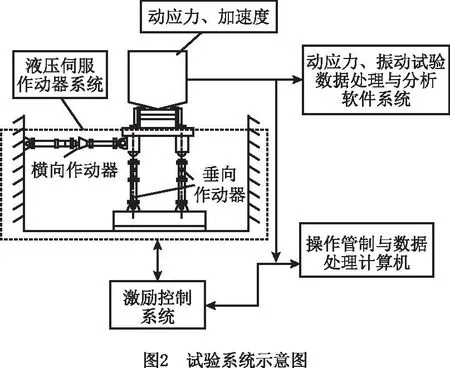
将整备状态车辆放置于试验台的4条轮对支撑梁上,通过试验台铰接装置连接车辆的一端车钩,另一端车钩与试验台不铰接,呈自由状态。每条轮对支撑梁下部连接2个垂向作动器,支撑梁一端连接1个横向作动器,作动器通过轮对支撑梁激励整备车辆在垂、横方向振动,激振信号采用实际的轨道谱或相应的待用谱模拟不同速度条件下受到不同轨道不平顺激励时的响应。测取车辆在不同线路激励条件下的车体振动加速度、动应力和悬挂的动挠度,计算平稳性数值/最大振动加速度和动应力等,试验系统如图2所示,振动试验如图3所示。

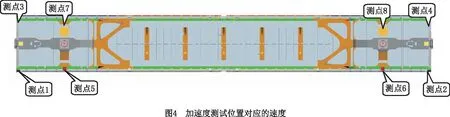
依托整车振动试验平台,振动试验模拟了90 km/h,100 km/h,110 km/h,120 km/h,130 km/h,140 km/h,150 km/h受到的激励。测试时,在车辆的每个轮子下方设置一个支撑梁,每个支撑梁有两个垂向和一个横向的电液激振器进行激振,用于模拟不同车速的轨道不平顺激励的情况。为了更好地进行仿真模拟,将问题简化为在测试点施加对应的测试加速度信号,即1,2,5,6位置施加横向和垂向加速度,3,4,7,8位置仅施加横向加速度,加速度测试位置如图4所示。

90 km/h～150 km/h的加速度信号在不同行驶速度的总采样长度如表2所示。

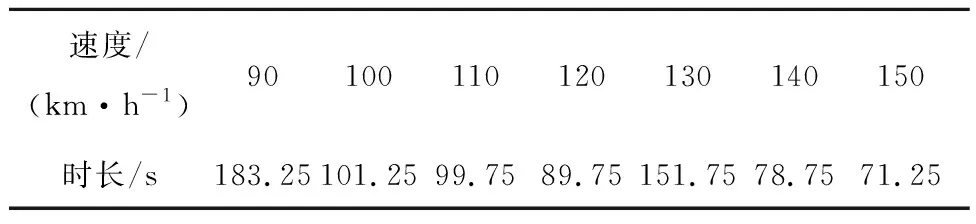
表2 不同行驶速度车辆加速度历史信号时长

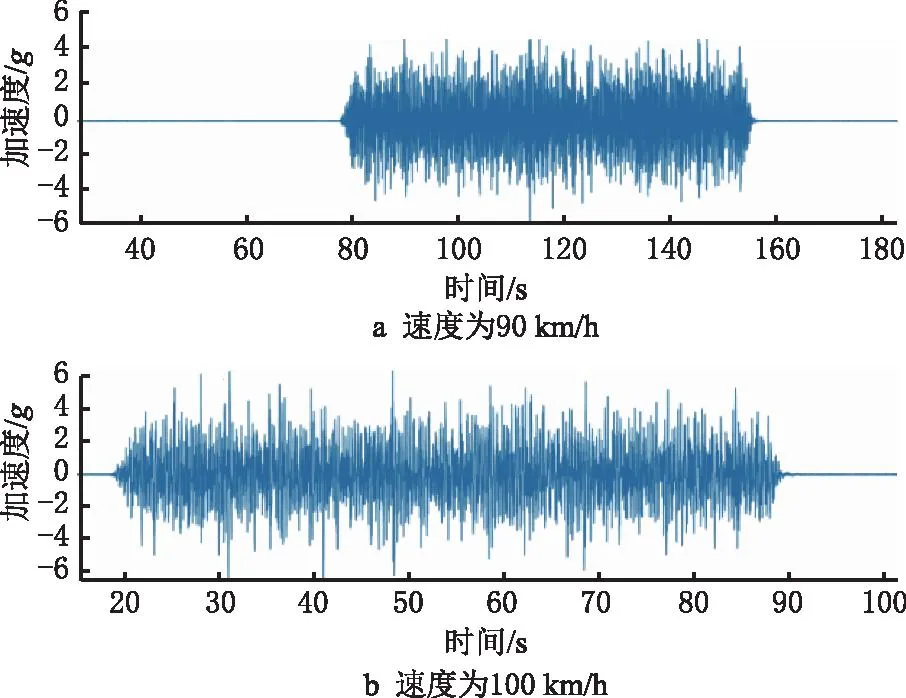
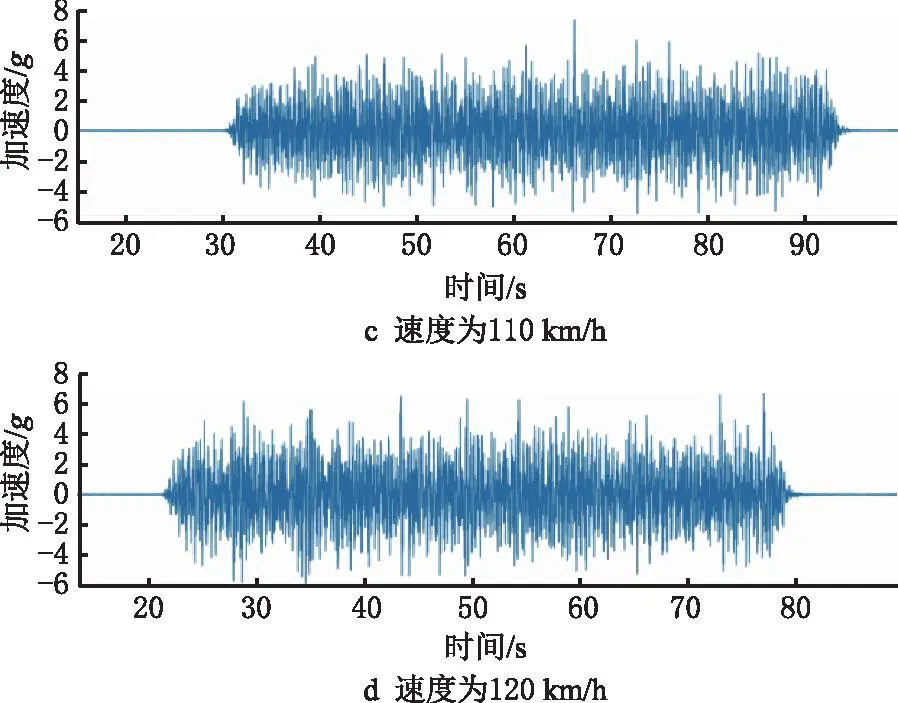
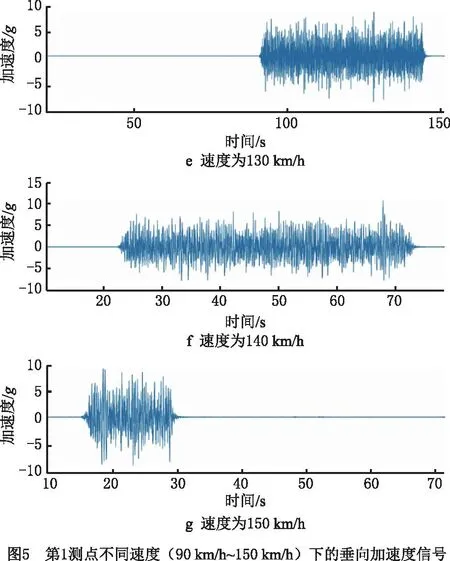
图5所示为不同行驶速度(90 km/h～150 km/h)对应的测量点1加速度信号,可见不同行驶速度的测量加速度信号不仅在记录时间上不同,激励所占的比例也不尽相同。

通过对上述信号进行频域分析,得到信号对应的频域功率谱信号,如图6所示。

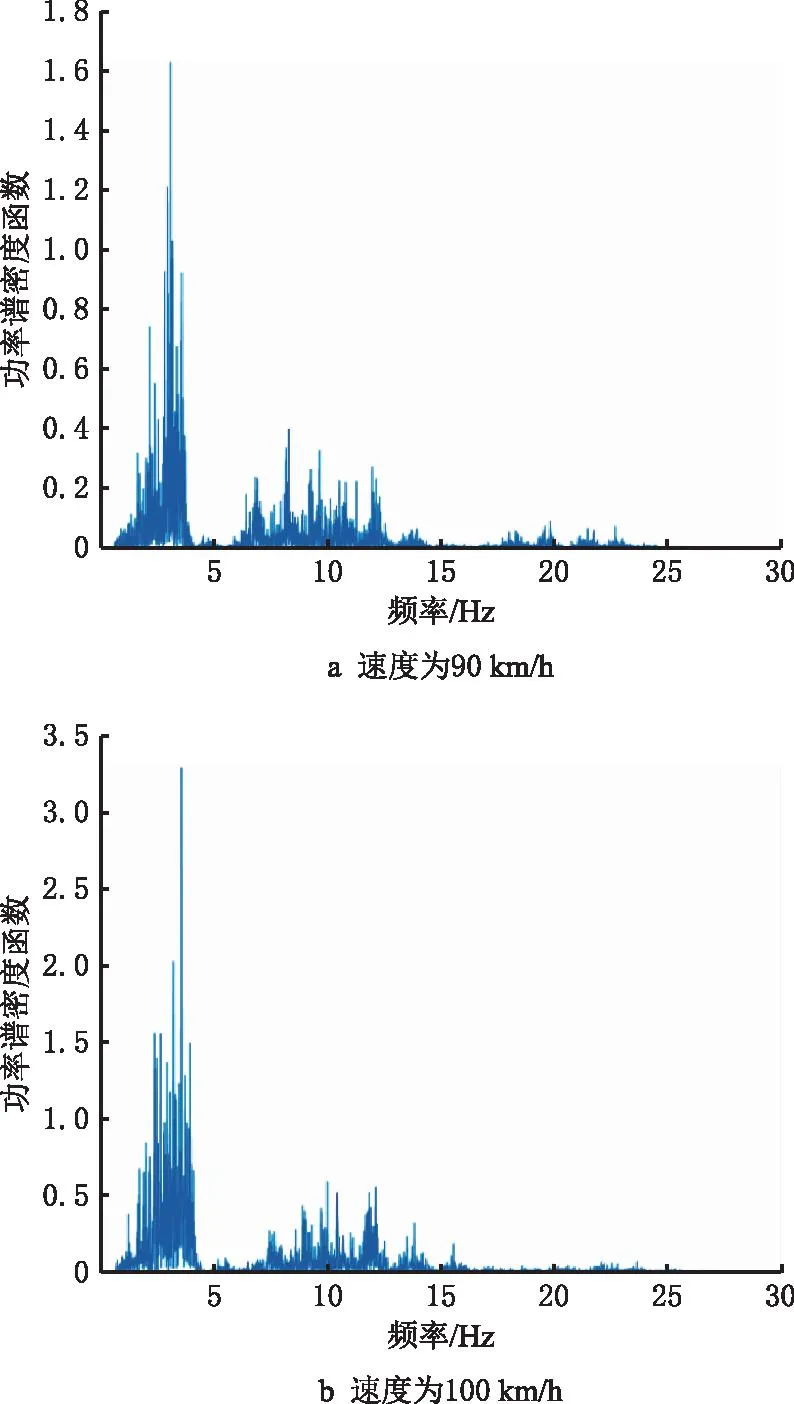
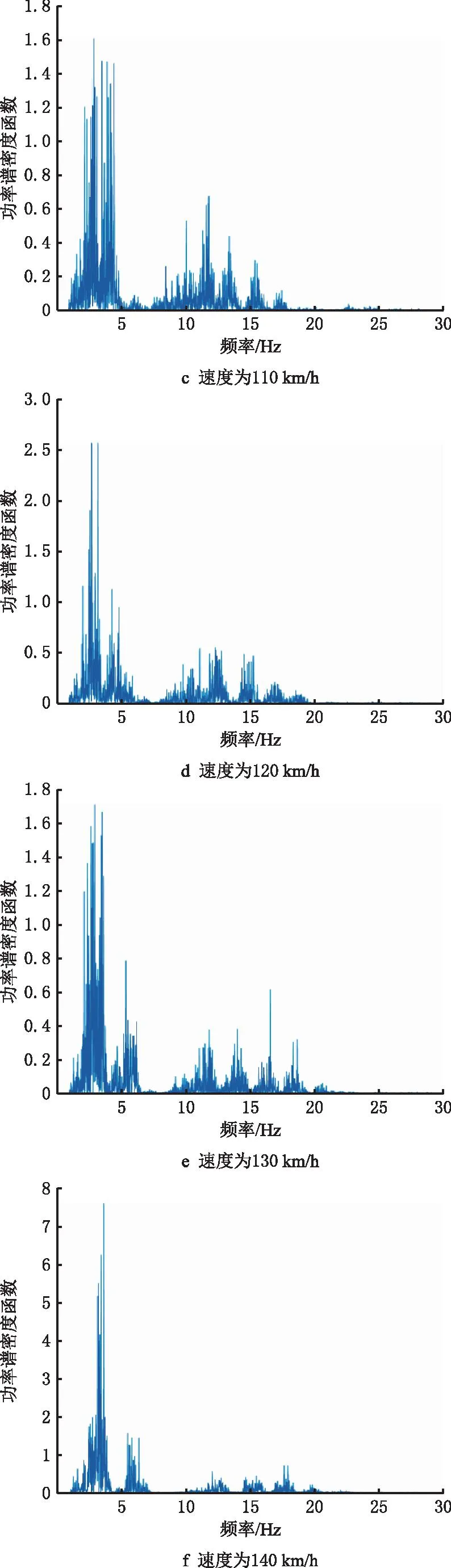
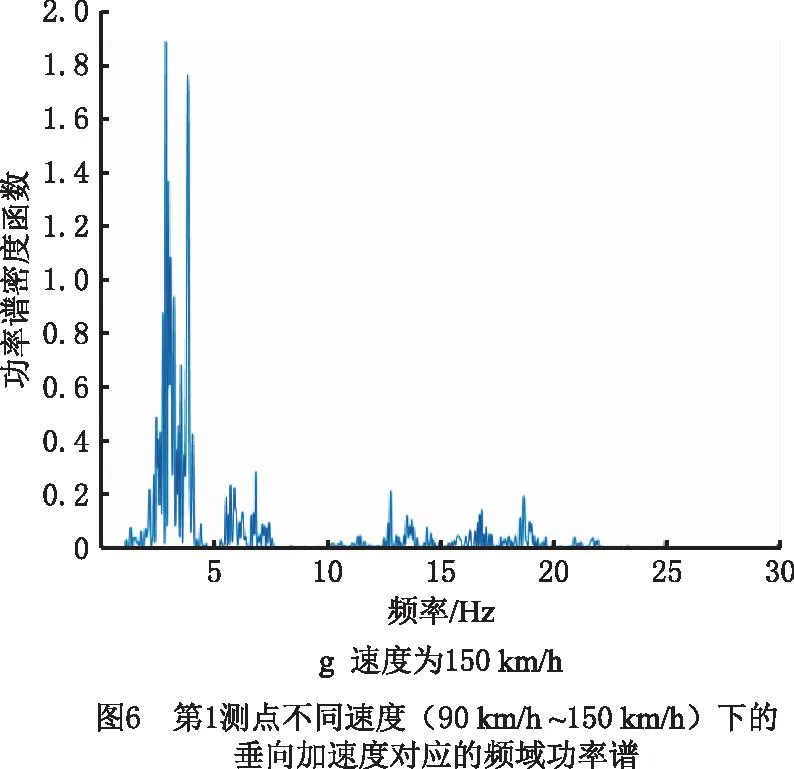
图6中不同载荷的功率谱即为式(8)中的Sqq,将其代入式(8)即可求解各焊线的结构应力功率谱。由频域谱可见,车体在不同行驶速度下均受到频率在2.5 Hz～5 Hz的较强激励,但在110 km/h,120 km/h,130 km/h工况下,在10 Hz～20 Hz也受到较强的激励;对于130 km/h,140 km/h工况,载荷在5 Hz～7 Hz受到的激励也达到一个小峰值;在140 km/h,150 km/h工况下,激励在10 Hz～20 Hz所占份额较小。通过图6f和图6g可以看出,上述两种速度运行下所测的时间较短,影响不明显。

2.2 模态分析与模态结构应力

基于整车频域试验分析结果开展模态和模态结构应力分析。首先对模型进行模态分析,截取其中14阶模态,模态频率如表3所示。

表3 车体前14阶模态

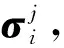
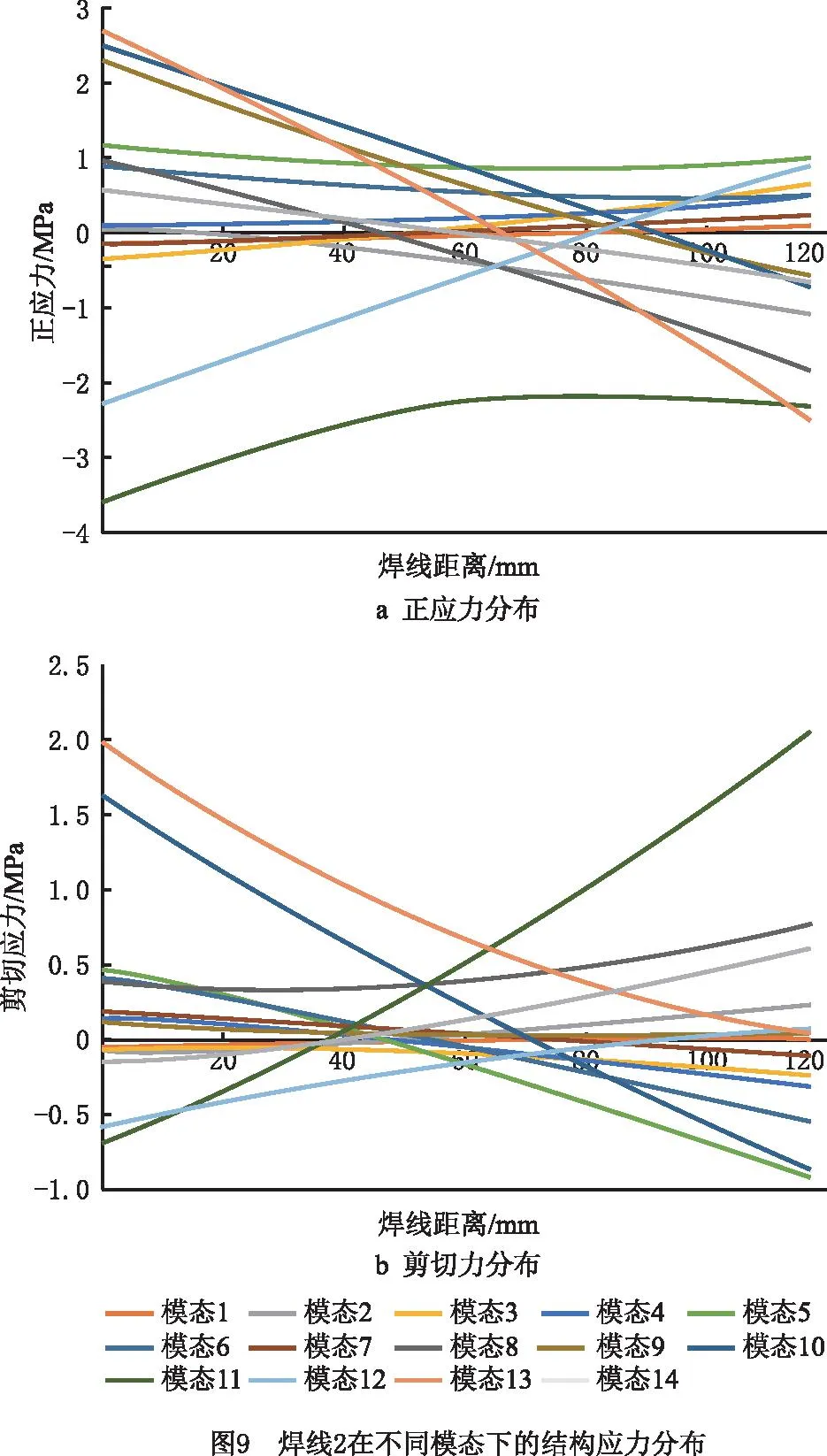
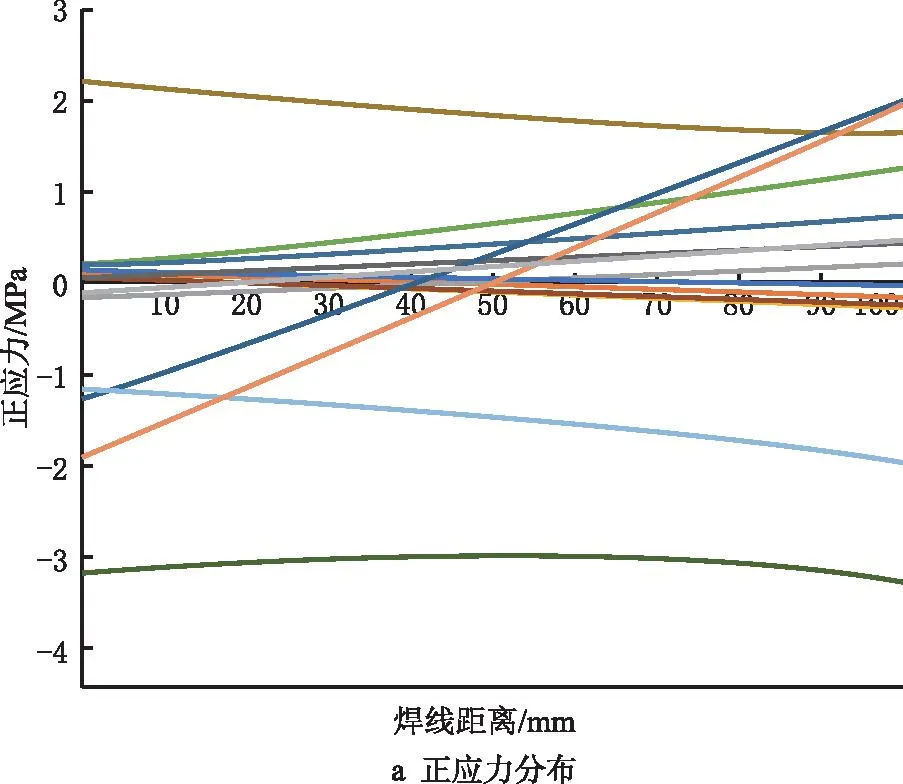
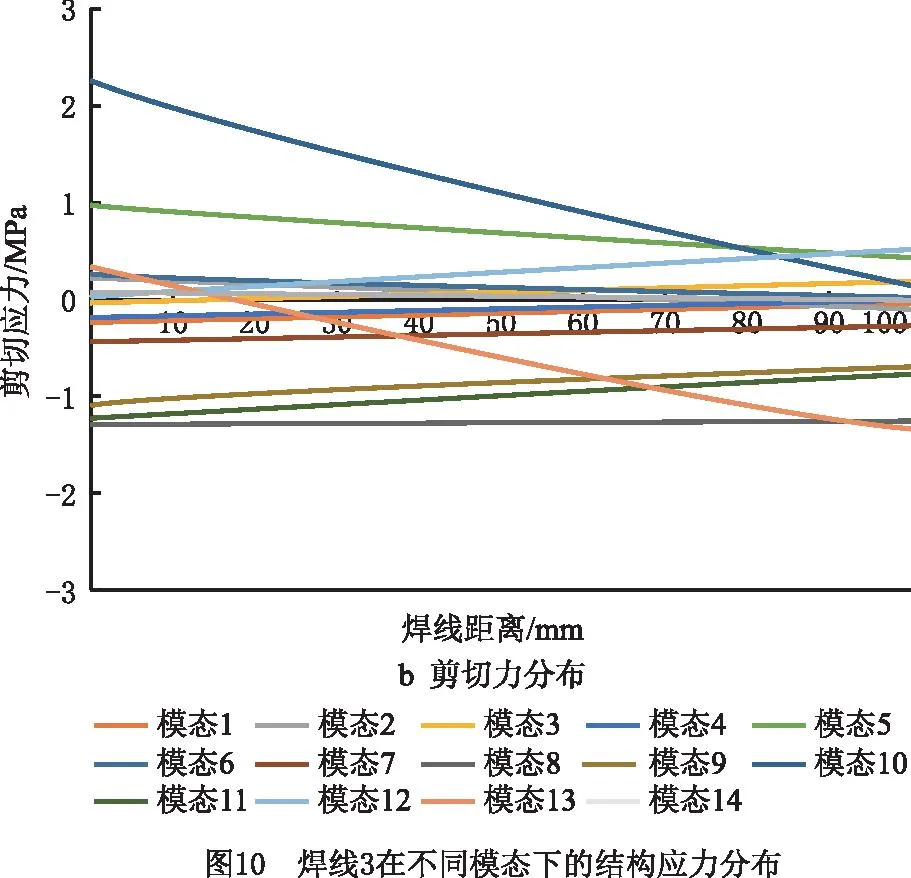
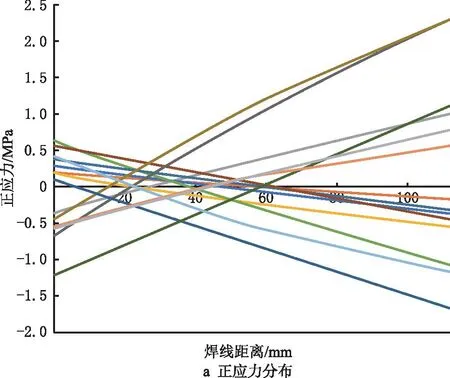
2.3 频域响应与模态坐标

前14阶模态坐标在不同行驶速度下的上述12组激励信号作用时的频率响应如图13所示,模态坐标在不同速度激励下的频率响应如图14所示。

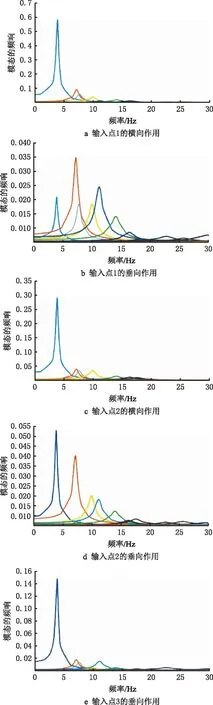
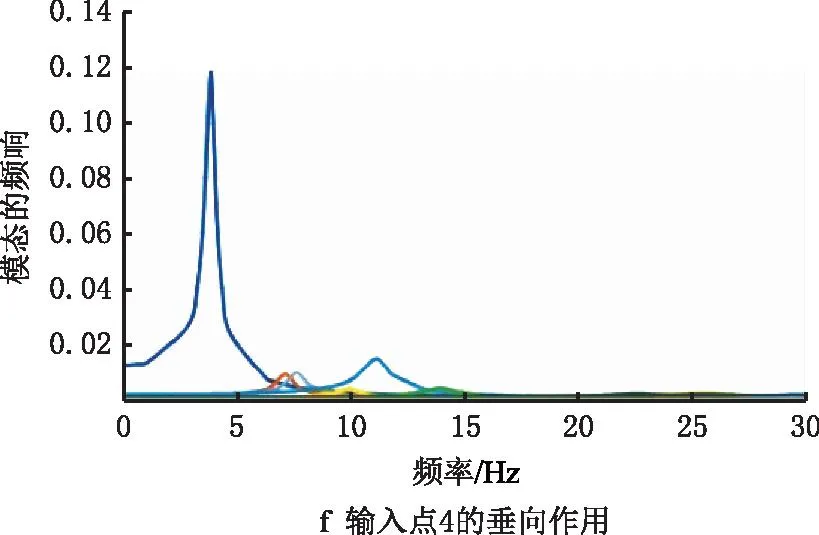
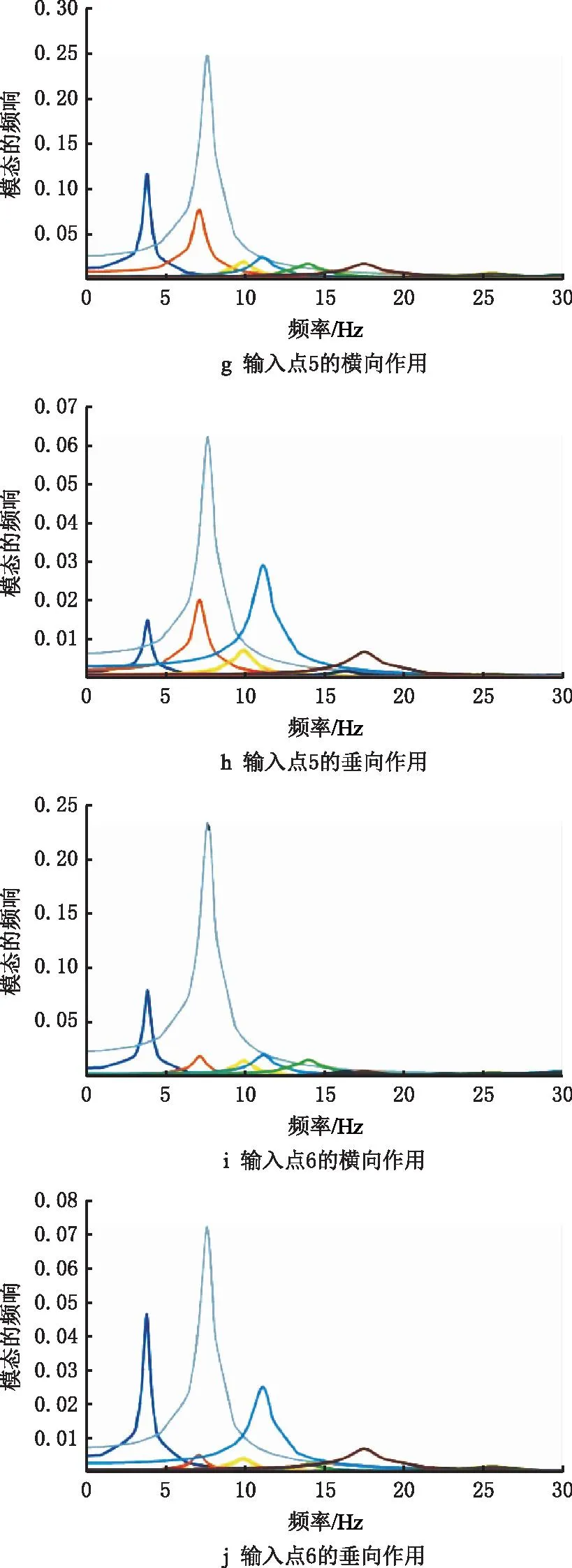
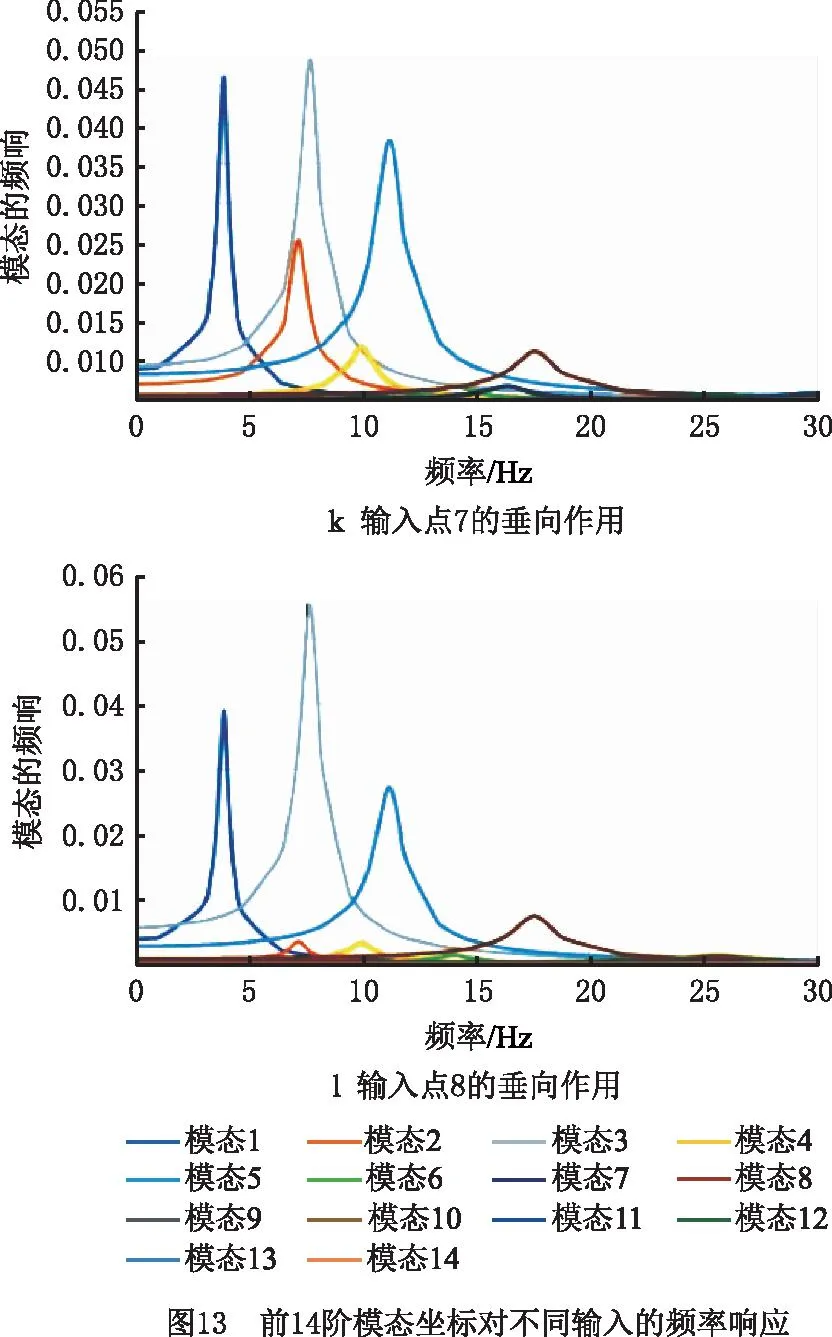
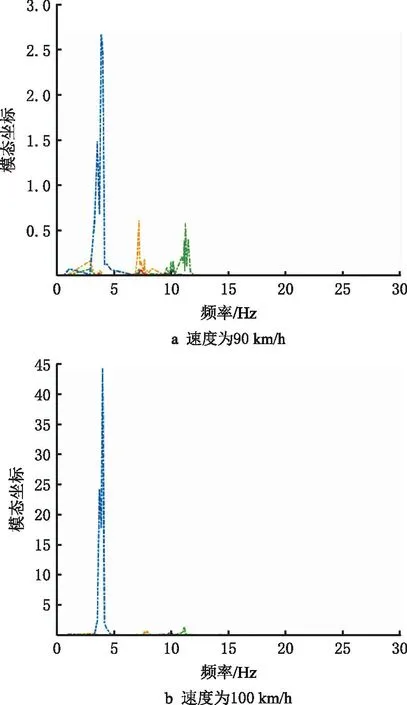
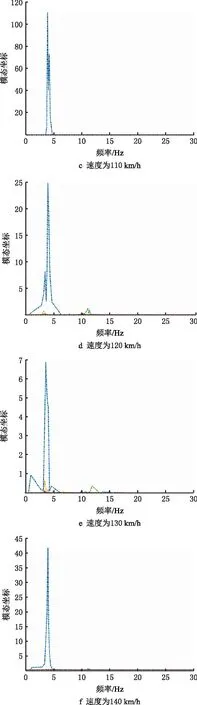
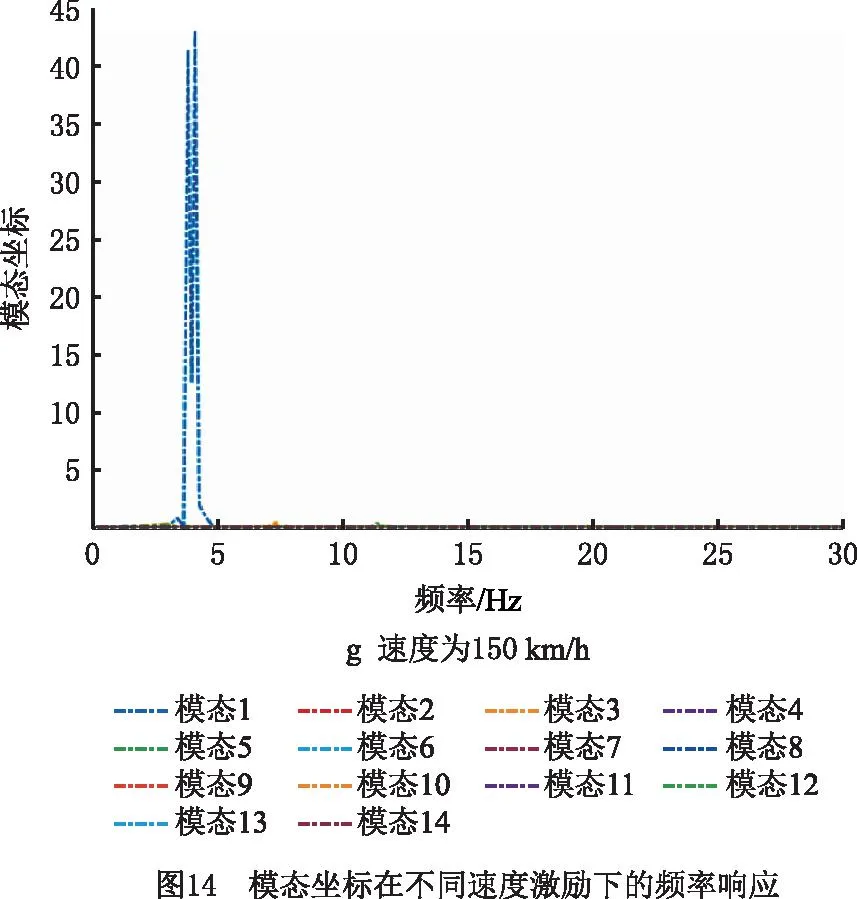
由图14可见,无论在哪种载荷作用下,结构第1阶段振型的模态坐标均为最大值。在90 km/h运行速度下,结构的第3阶段和第5阶段模态响应也比较突出。

2.4 结构应力功率谱与等效结构应力功率谱

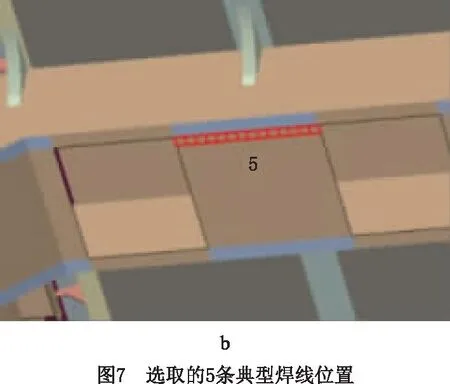
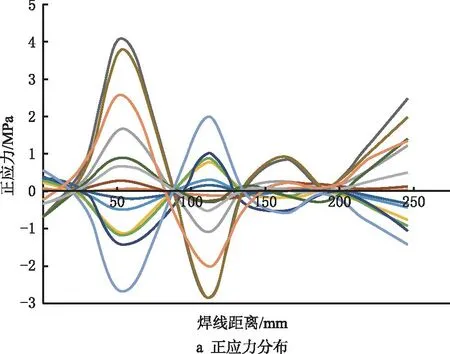
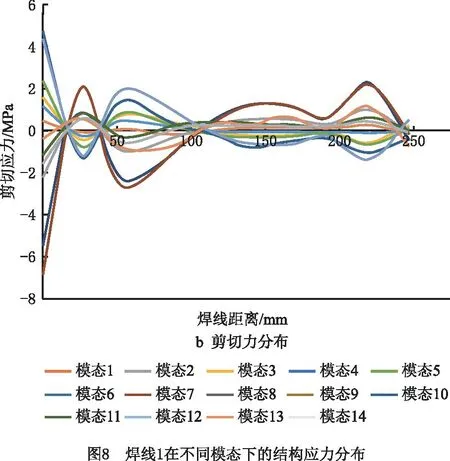
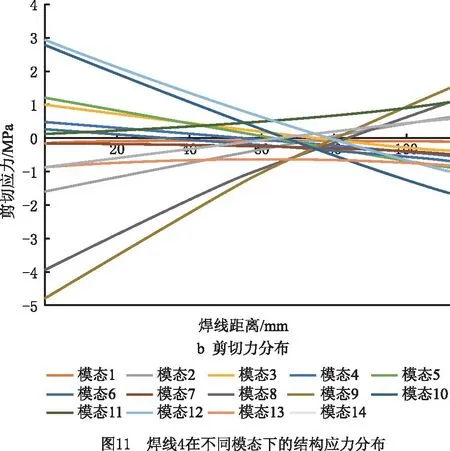
分析不同模态下正应力和剪切应力的大小后,为保证车辆可靠性,取消焊缝1处的内凹结构,以应力最恶劣的焊线4为例,计算焊线上不同节点(节点1和节点5)的结构正应力于结构剪切应力的功率谱(对应120 km/h的行驶速度载荷)。从图15可见,对于节点1,其结构正应力和结构剪切应力的功率谱在3 Hz和11 Hz取得峰值,对应车体结构的第1阶和第5阶振型。相对而言,结构的剪切应力功率谱更高,然而相对于节点5,节点正应力和剪切应力都在11 Hz取得峰值,值得注意得是,虽然从图13可以看出模态1的模态坐标远大于模态5,但是结合图15结构在不同模态下的结构应力分布可见,模态5下焊接的结构应力高于模态1。因此,评估各个模态对疲劳损伤的影响应结合模态坐标和各模态下焊线的结构应力分布情况综合考虑。

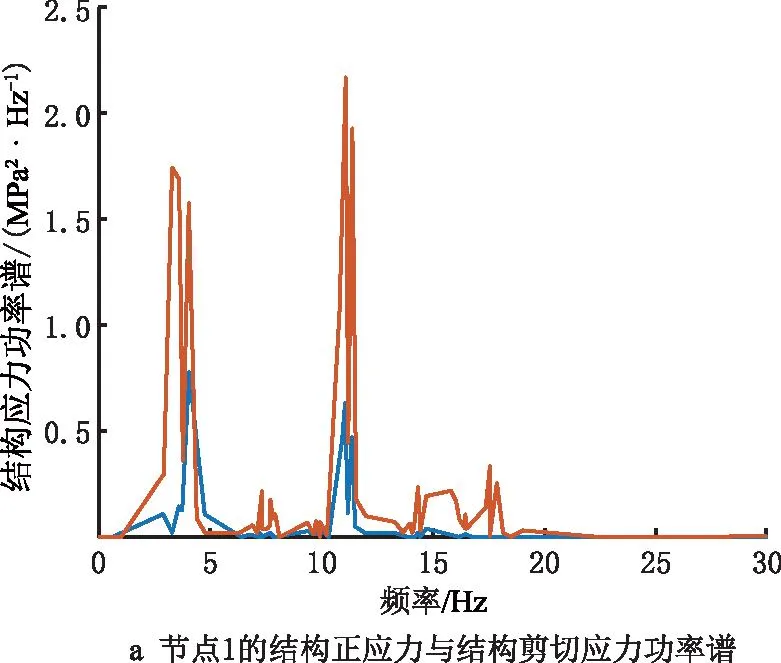
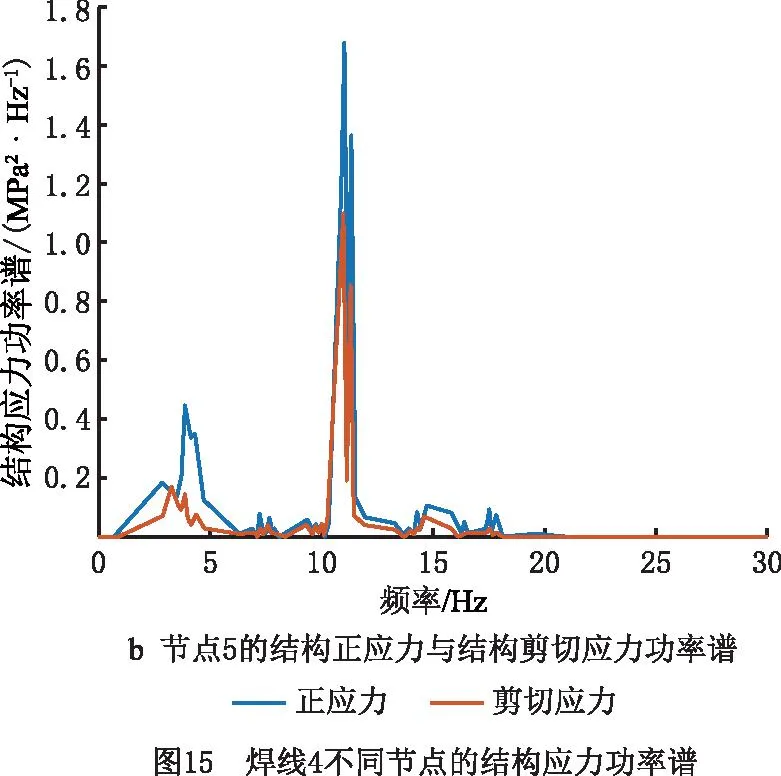
在得到焊线上各个节点的结构正应力与结构剪切应力的基础上,根据正应力与剪切应力的相关程度计算结构的等效结构应力功率谱,如图16所示。

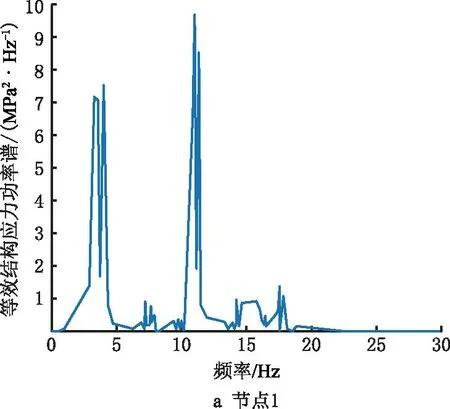
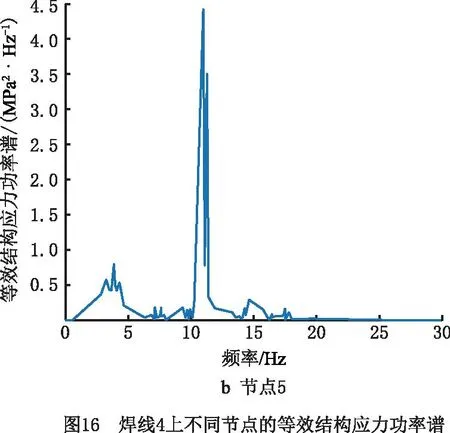
2.5 疲劳损伤与寿命估计

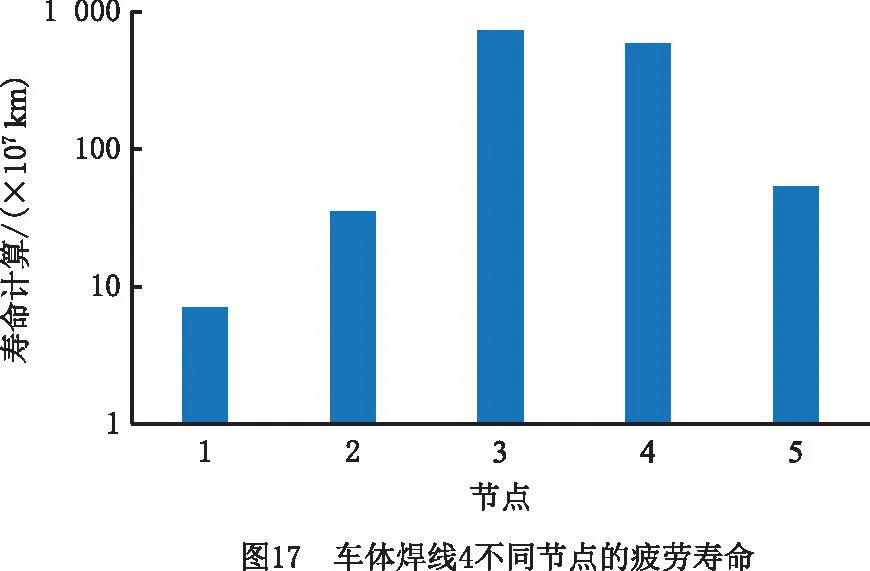
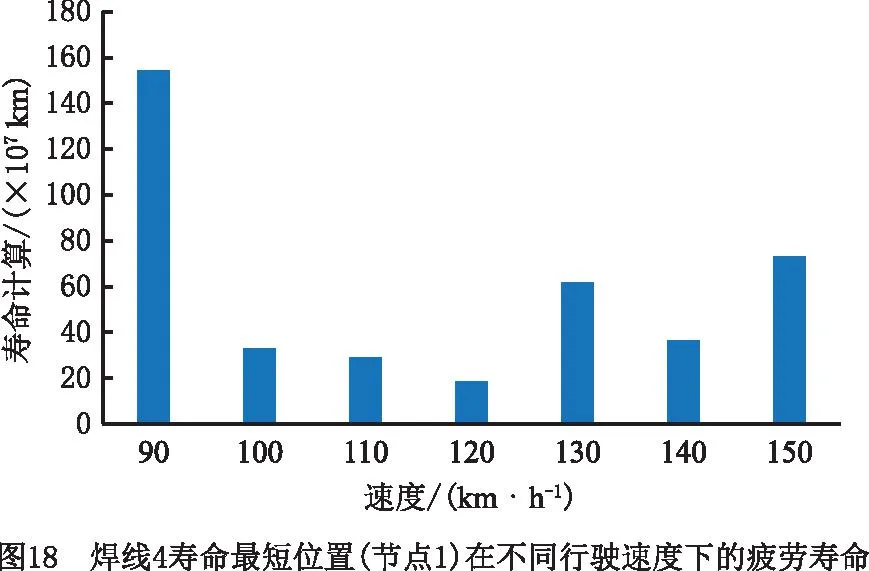
利用计算得到的等效结构应力功率谱及其概率密度分布函数求出等效结构寿命。车辆5个焊线上的节点在模拟行驶过程中的疲劳寿命情况如图17所示,图中的寿命根据车辆在90 km/h～150 km/h行驶历程均相同的情况下估算得到。从图中可见,焊线2,3,5均相对安全,按照铁路货车25年500×104km运行里程考核,焊线上所有节点的疲劳寿命均满足运营要求。图18所示为焊线4上寿命最低点在不同行驶速度下的疲劳寿命。可见90 km/h时车辆的行驶寿命最长,120 km/h时行驶寿命最短,这一现象可能由不同行驶速度下产生的激励频率与车体固有频率不同导致。

根据以上分析,降低焊线4中节点1在3 Hz和11 Hz时的正应力和剪切应力,具体将结构的端部加强座的高度增加10 mm,加强座宽度增加5 mm,消除应力集中点,降低应力功率谱,采用上述方法重新校核,该位置的疲劳寿命提高至510×104km,计算结果满足铁路货车运行要求。

3 结束语

本文在研究既有疲劳分析方法的基础上,针对大型复杂焊接结构多轴随机振动疲劳问题,提出基于结构应力的多轴疲劳频域分析方法。该方法将模态分解和结构应力有效结合,通过模态叠加方法高效计算出焊线的结构应力,并得到各模态对结构应力的贡献。考虑焊线受到的正应力和剪切应力,结合PDMR多轴疲劳准则,计算基于等效结构应力的功率谱,最后通过Dirlik概率模型求得结构的疲劳损伤,完成结构的疲劳寿命评估。该方法充分兼顾频域的高效性与时域载荷的完整性和准确性,针对焊接结构振动疲劳问题,快速确认优化方案的可行性,并在工程实际中进行了应用。

为充分验证该方法在轨道车辆上的可行性和准确性,后期将进一步开展整车线路试验,完成振动疲劳仿真分析与试验的对比,开展产品的剩余使用寿命预测[26],并结合拓扑优化等技术[27],在提高产品使用寿命的同时进行准确评估。