波浪条件下小型回转体高速入水动力学特性研究

李江昊，王光越，郭林祥

（1.清江创新中心，湖北 武汉 430076；2.中国船舶集团有限公司第七一〇研究所，湖北 宜昌 443003；3.中国特种飞行器研究所，湖北 荆门 448035）

0 引言

随着现代战争的发展，为了提高突防能力，水中武器多向高速迈进，高速入水过程涉及的瞬态冲击、自由液面破碎、流固耦合等问题存在强非线性特征，一直是海军装备研究的热点和难点[1]。同时未来海战也不可避免地会在波浪环境中发生，波浪的存在改变了入水自由液面的形态，而流场特性与物体运动呈强耦合影响，波浪环境会影响鱼雷等跨介质武器入水时所受水动力载荷和弹道稳定性，因此探明波浪条件下跨介质武器入水载荷及运动姿态特性具有重要的实际意义[2]。

针对回转体高速入水的问题，国内外学者开展了大量的研究[3]。顾建农[4]等人研究了不同头型以不同速度水平入水的空腔发展以及入水弹道。施红辉[5]等人用高速摄影仪拍摄了回转体高速入水过程中的空腔演化形态以及空气夹带等非线性流动现象。TRUSCOTT[6]等人采用试验手段，并运用高速摄影技术，对弹体斜入水的过程进行了捕捉，得到了弹体斜入水下的运动轨迹。SHI[7]等人采用任意欧拉-拉格朗日（ALE）方法研究了弹性水下机器人入水过程中头部形状参数、壳体厚度、入水速度对弹性水下机器人入水冲击过程中加速度、压力、应力和结构变形的影响。LYU[8]等人在三维多分辨率光滑粒子（SPH）的框架内进行了自由落体救生艇的入水动力学分析，结果表明SPH 模型与基于网格的求解器相比能更好的捕捉飞溅射流和散射液滴的能力。但以上高速入水研究均在静水中开展，未考虑波浪环境的影响。

对于波浪环境下回转体入水，李治涛[9]基于流体体积法（VOF）模拟了高速旋转射弹波浪中入水过程，分析了波面不同位置入水弹体空泡形态和载荷特性变化规律。储慧林[10]基于商业软件Fluent建立了二维数值水槽，实现了规则波的模拟并实现波浪中鱼雷垂直及倾斜入水过程，得到了鱼雷波浪条件下入水砰击压力及弹道特性。杨晓光[11]等人开展了平静水面，遭遇波面不同位置和不同波高下的入水试验，得到了回转体入水加速度和姿态角，结果表明由于波面的存在改变了回转体入水的实际入水角度，且实际入水角度越小，入水冲击载荷越小。以上波浪环境下入水的相关研究多基于网格方法进行模拟，其处理大变形和快速移动的自由表面相较于无网格粒子法略有不足。

本文基于多级分辨率SPH 方法，并结合周期性边界技术，建立了回转体波浪环境下高速入水模型，进而研究了不同相位下的回转体高速入水空腔发展及回转体动力学特性，为波浪条件下跨介质武器的低载稳定入水提供基础性技术支撑。

1 数值计算方法

1.1 SPH 方法基本理论

本文采用了ANTUONO[12]等人提出的δ-SPH方法，该方法在模拟剧烈自由液面流动时足够准确和稳定。由于其密度扩散项的增加，其可以在很大程度上减少由弱可压缩假设引起的非物理压力噪声，δ-SPH 方法的主要控制方程如下：

式中：连续性方程和动量方程右侧最后一项分别为密度耗散项和人工粘性项[15]，其中的符号i和j表示粒子编号，D Dt表示跟随流体微团运动的导数；r , v,p,ρ ,V,m分别代表流体的位置、速度、压力、密度、体积和质量；g为重力加速度；系数α，δ根据不同问题取相应的值；W为核函数；h为光滑长度；c0，ρ0分别为流体声速和流体密度。

1.2 SPH 数值造波技术

为了探究波浪条件下回转体高速入水的动力学特性，本文基于有限水深波浪理论建立了波浪数值造波模型[15]。其中，x方向上波面方程为

式中：ω=2π/T，T为波浪周期；k= 2 π /L，L为波长；δ为初始相位，取0 到2π 之间的值。其中L可以根据色散方程得到：

式中，d为静水深度。速度势函数为

本文在三维波浪数值水池中，对波浪的入口和出口区域采用了周期性边界技术[15]。当流体粒子流出计算域并进入右侧的出口区域时，粒子携带着所有的物理信息，立刻转移到流体区域的最左侧，作为计算域的流入粒子。出口区域和入口区域的虚粒子由流体域两侧的粒子复制生成，作为计算域的边界条件。采用周期性边界后，可以模拟波浪的稳定流动，出口边界和入口边界的流量可以保持守恒。

1.3 入水数值模型验证

为了验证数值模型的计算精度，本文对小型回转体高速入水进行数值模拟，通过与论文结果[16]对比，验证了小型回转体高速入水的数值计算精度。数值模型中回转体与水面的夹角为20°，入水速度为70 m/s。水域尺度为10 m×5 m×2 m，小型回转体模型如图1所示，实验模型转动惯量

图1 实验模型图Fig.1 Experimental model diagram

本文采用SPH 数值方法进行模拟，图2 为实验[3]与仿真不同时刻流场对比示意图，图中上半部分为实验流场，下半部分为仿真流场，可以看到在实验中，回转体在高速入水初期处于超空泡状态，回转体入水后被超空泡包裹，在SPH 模拟的结果中也可以得到同样的水动特性。将仿真结果与实验结果对比，发现同一时刻，仿真与试验的流场特性、空泡形态、回转体入水深度能够较好吻合，结果表明模拟中使用的SPH 数值模型可以捕捉空腔的发展情况从而验证了SPH 模型在模拟回转体高速入水上的可靠性和预测能力。

图2 不同时刻实验与仿真入水流场与弹道对比Fig.2 Comparison of flow field and trajectory of experimental and simulated inlet water at different time

由于该实验模型关于纵平面对称，因此轴向加速度是影响回转体运动状态的重要力学特性，为了进一步验证仿真模型的载荷预测精度，本文对轴向加速度实验结果[3]与轴向加速度仿真结果进行对比，如图3所示。图中红色曲线代表SPH 仿真结果，黑三角代表实验结果，通对比过可以得出，实验结果与仿真结果曲线变化规律一致，且实验与仿真轴向加速度峰值相对误差约为2.1%。

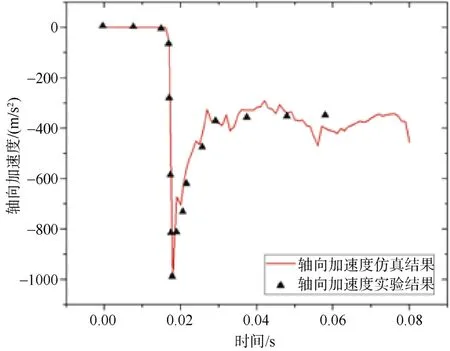
图3 实验与仿真轴向加速度对比Fig.3 Experimental and simulated axial acceleration

2 数值模型建立与典型工况模拟

2.1 数值模型的建立

为了探究波浪条件下小型回转体高速入水动力学特性，首先要建立三维数值水槽。本文生成的波浪水槽，如图4所示，波浪参数为波幅为0.5 m，波长为6 m，波浪周期为2.8 s。为了探究波浪条件下回转体高速斜入水动力学特性，挑选了回转体波浪条件下某一入水时刻作为典型工况分析，此刻高速入水的回转体与水平面的夹角为20°，速度为70 m/s，为了方便理解，我们将回转体入水速度与水平面的夹角叫做名义入水角。

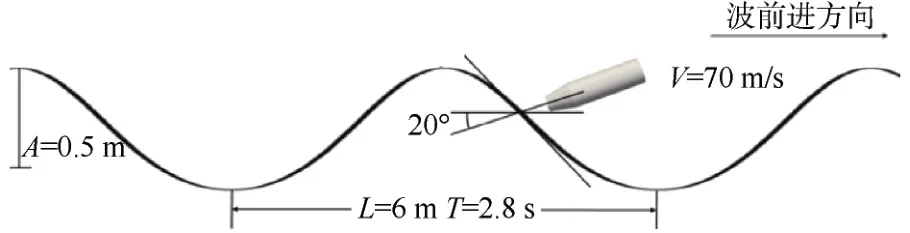
图4 回转体波浪入水典型工况示意图Fig.4 Schematic diagram of typical working conditions of wave entry of a rotary body

基于SPH 模型的波浪条件下小型回转体高速入水仿真结果图如图5所示，从三维速度云图中可以看出，当回转体以70 m/s 入水时，回转体撞击波节，头部周围水域速度增大，并以椭圆形形状进行速度传递，直到波节自由面流体速度与波峰处速度一致。

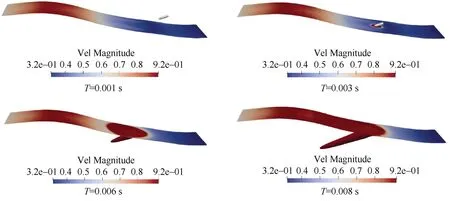
图5 回转体波浪条件下高速斜入水速度云图Fig.5 Velocity cloud diagram of high-speed oblique entry under wave conditions of a rotary body

图6 给出了波浪条件下回转体高速斜入水过程中的空泡发展历程，通过自由液面提取程序，将SPH 粒子图转化为清晰光顺的自由液面云图，并提取了处于工作区域内的波面，并成功捕捉到了回转体高速入水空腔发展情况。由图6 可以看出，在初始阶段，回转体撞击波节形成空泡雏形，在侵入阶段，回转体与流场不断作用，空泡逐渐形成，包裹在回转体周围，可以看出空泡壁比较光滑且尺寸不断增大，并且在回转体入水前端波面造成液面隆起的现象[17]。

图6 回转体波浪条件下高速斜入水空泡示意图Fig.6 Schematic diagram of high-speed oblique water cavitation under wave conditions of a rotary body

2.2 波浪对回转体动力学特性影响

图7 给出了静水条件下入水角20°与波浪条件下名义入水角20°时的无量纲轴向加速度对比图，由图可以看出，当回转体分别在静水和波浪条件下入水时，波浪条件下回转体入水载荷曲线与静水条件下回转体高速入水载荷曲线趋势一样，但峰值比静水条件大。分析原因，波面的存在改变了回转体与水面的实际夹角，我们将波面与回转体的夹角定义为实际入水角，此刻回转体波浪条件下实际入水角大于静水条件下实际入水角，因此，回转体轴向载荷峰值波浪条件较静水条件大，当回转体完全入水后，其轴向载荷趋于相等。

图7 静水与波浪条件下回转体加速度对比Fig.7 Comparison of the acceleration of a rotary body in still water and wave conditions

图8 给出了静水条件下入水角20°与波浪条件下名义入水角20°时的回转体俯仰角对比图，由图可以看出，此刻波浪条件下回转体俯仰角变化较静水条件下俯仰角变化小，即弹道稳定性越高。分析原因，波浪条件下回转体实际入水角大于静水条件下实际入水角，而实际入水角越大，弹体转动角速率减小，运动稳定性强[18]，因此波浪条件下回转体弹道较稳定。

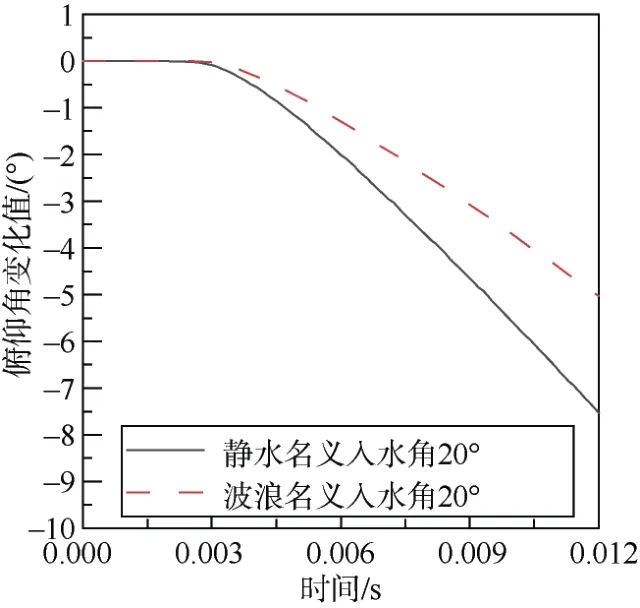
图8 静水与波浪条件下回转体俯仰角对比Fig.8 Comparison of the pitch angle of a rotary body in still water and wave conditions

3 波浪条件下不同相位高速入水

3.1 不同相位高速入水工况分析

为了进一步分析波浪对回转体高速入水动力学特性影响，本节将在上一节的基础上，进一步探索回转体在不同波浪相位下回转体高速斜入水模型，通过分析不同相位下高速回转体斜入水的轴向合力与偏转角，掌握波面环境下回转体高速入水的载荷特性与运动姿态，回转体入水示意图如图9所示。

图9 不同波浪相位回转体斜入水示意图Fig.9 Schematic diagram of oblique entry of different wave phases

波浪参数与上节一样，回转体模型与速度大小也保持一致，回转体入水速度与水平面的夹角为20°。入水点相位分别为波峰、波谷、1 号波节、2号波节。由上一节规律可知回转体不同波面条件下入水，发生改变的是波面的波倾角的大小，从而改变了回转体的实际入水角。由计算可知，波峰处和波谷处的波倾角为0°，1 号波节处的波倾角为14°，2 号波节处的波倾角为-14°。回转体正在波峰、波谷、1 号波节、2 号波节处的实际入水角分别为20°、20°、34°、6°，具体入水特征参数如表1所示。

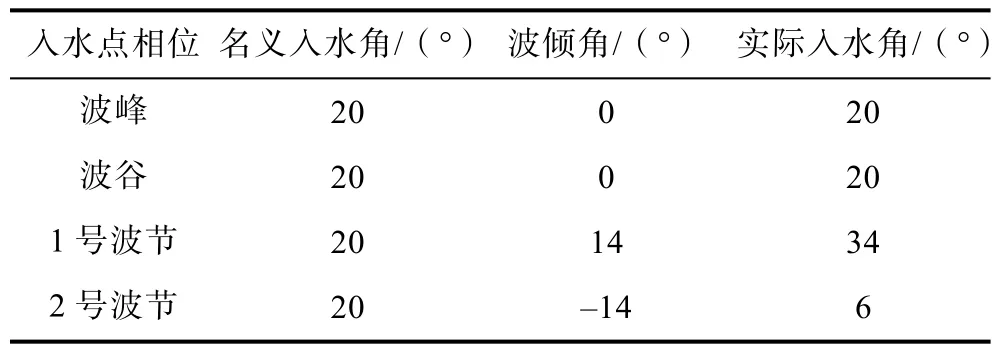
表1 回转体波浪条件下不同相位入水特征参数Table 1 Characteristic parameters of water entry of different phases under wave conditions of a rotary body

3.2 不同相位高速入水弹道特性分析

图10 为SPH 三维入水模型模拟的1 号波节处回转体高速入水模拟图，从图中可以看到回转体在1 号波节处入水，入水后产生的空腔包裹在回转体周围，且1 号波节处回转体入水初期弹道较为稳定，未发生偏转。

图10 1号波节处回转体高速入水模拟图Fig.10 Simulation diagram of high-speed water entry of rotary body at the No.1 wave joint

图11 为2 号波节处回转体高速入水模拟结果图，从图中可以看出，当T=0.008 s 时回转体弹道发生失稳，发生“跳弹”现象，回转体头部冲出水面。由表1 可知回转体2 号波节处入水实际入水角等于名义入水角20°与入水点波倾角-14°的差值。由静水条件下入水角度与回转体动力学特性关系可知，随着入水角度减小回转体俯仰角变化增大，弹道失稳概率增加。由于波倾角的存在，此时回转体高速入水实际入水角为6°，极容易发生俯仰角变化过大，而发生“跳弹”现象。

图11 2号波节处回转体高速入水模拟图Fig.11 Simulation diagram of high-speed water entry of a rotary body at the No.2 wave joint

图12 为波谷和波峰处回转体高速入水示意图，由图可知，波峰处入水较波谷处入水，回转体运动姿态更加稳定。分析原因：由表1 可知回转体波峰处入水实际入水角等于波谷处实际入水角，但波峰处入水回转体更接近自由液面，受到水体的上下压强差较波谷处小，因此姿态较波谷处稳定。

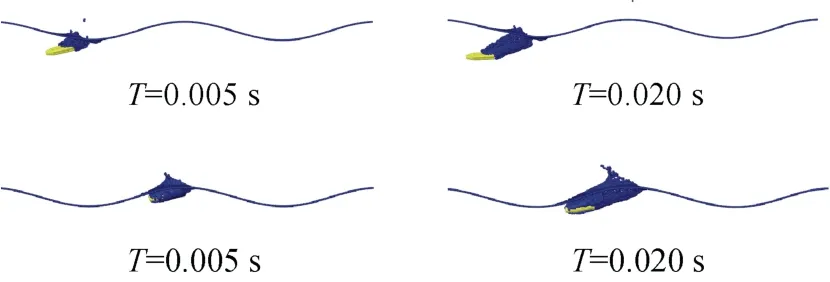
图12 波谷波峰处回转体高速入水模拟图Fig.12 Simulation diagram of high-speed water entry of a rotary body at trough and crest

为了更好地分析不同相位下回转体运动姿态变化情况，本节给出了不同相位下回转体俯仰角和偏航角随时间变化曲线图。由图13 可以看出，1号波节入水俯仰角变化最小，波峰和波谷俯仰角变化次之，2 号波节俯仰角变化最大，即2 号波节下回转体入水姿态最不稳定，易发生失稳情况。分析原因，1 号波节回转体实际入水角最大，在轴向载荷受力增大的情况下，入水稳定性得到了增加。2号波节回转体实际入水角最小，虽然所受到的轴向载荷最小，但回转体姿态却变得不稳定，最容易发生失稳。

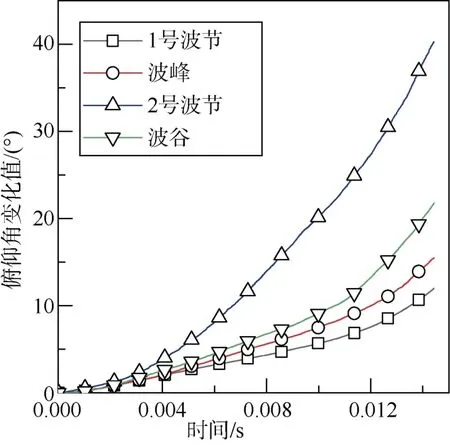
图13 不同相位入水俯仰角变化值Fig.13 Variation of pitch angle in different phases of water entry

3.3 不同相位高速入水载荷运动特性分析

入水相位的改变不光影响了回转体入水弹道，也影响入水初期轴向加速度峰值。图14 为SPH 三维入水模型模拟的不同相位下回转体高速斜入水的轴线加速度时历曲线。由图中可以看出不同相位下入水轴向加速度峰值不同，但入水后期入水轴向加速度值大致相同，说明波面的存在对回转体入水载荷的影响主要体现在入水初始时刻，从曲线中可以看出波峰与波谷相位下回转体轴向加速度峰值相同。分析原因在于波峰与波谷的回转体实际入水角相同，而1 号波节相位下回转体轴向加速度最大，2 号波节相位下回转体轴向加速度最小，分析原因在于1 号波节回转体实际入水角最大，2 号波节回转体实际入水角最小。

图14 不同相位回转体斜入水加速度对比Fig.14 Comparison of oblique water entry acceleration of different phased vehicles

4 结束语

本文基于光滑粒子流体动力学（Smoothed Particle Hydrodynamics，SPH）方法，建立了基于SPH 法多分辨率刚体入水的六自由度响应模型，实现了波浪环境下小型回转体高速入水过程的数值模拟，对波浪环境中回转体入水特征参数、运动姿态以及波浪相位对回转体入水动力学特性影响规律进行探索，得出以下结论：

1）波面的存在改变了回转体入水冲击载荷和运动姿态，主要原因是波浪改变了回转体与自由液面的夹角。由于波倾角的影响，回转体1 号波节处实际入水角大于名义入水角，2 号波节处实际入水角小于名义入水角，波峰与波谷处实际入水角与名义入水角相等。

2）入水点相位对回转体载荷和弹道特性有直接影响，1 号波节处入水载荷最大，但入水弹道更稳定；2 号波节处入水载荷最小，但弹道更易发生失稳；波峰波谷处载荷与弹道相近。

针对波浪条件下跨介质武器高速入水过程的水动力载荷预报和初始姿态变化预测等难题[19]，通过开展波浪条件下回转体高速入水过程的数值模拟，对波浪环境下回转体入水过程中的运动姿态、冲击载荷及流场演变特性等进行研究，为波浪条件下跨介质武器的低载稳定入水提供基础性技术支撑。