基于 ANSYS Workbench异型臂架模态及谐响应分析*

王雪虎,谭勇军,邓阳光

(湖南兵器轻武器研究所有限责任公司, 湖南 益阳 413000)

0 引 言

悬架是决定汽车舒适性和控制性的关键部位,它是汽车的车架(或承载式车身)与车桥(或车轮)之间的一切传力连接装置的总称,其作用是传递作用在车轮和车架之间的力和力扭,并且缓冲由不平路面传给车架或车身的冲击力,以减少由此引起的震动,保证汽车能平顺地行驶。悬架能保证车身和车轮同步运动,同时能够过滤车轮接触到的地面颠簸,使颠簸尽量少地传递到车内。因此,悬架是决定汽车舒适性和操控性的关键部位。悬架结构一般包括弹簧、减震器以及连接车轮和有导向作用的各种连杆。连杆也就是常见的各种摆臂。

随着汽车的高速化和大功率化发展,因振动所引发的弯曲裂纹、疲劳断裂、振动剧烈等导致结构破坏的问题时有发生,而传统的静态特性分析不具备分析上述动态结构破坏的能力,因此静态特性分析已不能满足生产需要。而模态分析和谐响应分析能够方便地了解结构的振动情况和薄弱环节,能为结构的优化设计和加工工艺的设计提供技术指导。因此,研究悬架关键结构件的动态特性已成为现代悬架设计的重要环节。

笔者以X型车的异形臂架为研究对象展开分析。异形臂架的振动根源主要是机械振动,此振动包括X型车在不平地面行驶时的冲击振动以及车身通过减振弹簧传递过来的振动。首先借助ANSYS软件对异形臂架进行模态分析,找出低阶固有频率和振型,通过振型找出异形臂架振动剧烈的区域,即结构刚度较小的区域;再通过振动谐响应分析,给异形臂架加载正弦载荷,频率范围为低阶固有频率。通过结构系统动响应参数位移、加速度、应力、应变找出具体影响结构动响应强度的频率,同时找出响应最为剧烈的区域,为以后的结构强化和实验监测提供有力的依据,也为国内异形臂架的设计研究提供技术支持。

1 有限元模型建立

文中所述异形臂架结构主要由钢板焊接而成,其前端装有和减震弹簧、液压缸连接的接口;中间4个安装孔,用来连接前车桥及轮胎;后端通过2个销轴、销轴安装座与车架连接。模型建模通过三维建模软件SolidWorks完成,因实际模型较为复杂,直接分析对计算机性能要求较高,计算所需时间较多,因此需要对用于仿真计算的模型进行简化,去除倒角、圆角及无关紧要的小孔等不影响整体结构性能的细小结构,以保证计算准确性,同时兼顾计算效率。异形臂架的材料主要为结构钢,质量密度ρ=7 890 kg/m3, 弹性模量E=206 000 MPa,泊松比μ=0.3,屈服强度为315 MPa,三维模型网格划分如图1所示。

图1 有限元模型网格划分

该模型结构较为复杂且为异形,而四面体网格适应性高,因此采用四面体网格进行划分,最终得到异形臂架网格单元总数为74 251个,节点数量为143 824个。

2 模态分析

2.1 模态分析理论

模态分析是结构件振动分析的关键步骤,通过模态分析可以计算出结构的固有频率和振型。将结构件的固有频率与外界激励频率进行比较分析,以避免因二者模态相近而引发共振现象,同时可根据振型结果所显示的薄弱环节,进行结构的优化设计。异形臂架作为车辆悬架的关键结构件,应尽可能避开可能存在的激振力固有频率范围,以保证车辆运行的稳定性。

对于一般结构而言,其动力学方程可表示为:

(1)

式中:[M]为质量矩阵;[C]为阻尼矩阵;[K]为刚度矩阵。

对于模态分析而言,{F(t)}=0,[C]=0,因此模态分析的运动方程可表示为:

(2)

由振动力学可知,结构的自由振动为简谐振动,其位移x可采用式(3) 进行表示:

x=Xcos (wt-ψ)

(3)

将式(3)代入式(2),可得:

[M]+w2[K]{x}={0}

(4)

通过对式(3)进行求解,得出自然角频率wi,自然频率为f=wi/2π 。每一个wi对应的向量{x}i为自然频率f=wi/2π对应的阵型[1]。

2.2 模态分析结果

有限元模型边界条件约束的合理性直接关系到模态分析求解的准确性。通过对异形臂架实际安装方式的综合分析,最终对异形臂架的螺栓安装孔及销轴安装孔进行固定约束。零件间靠焊接固定,焊缝强度足够,焊缝连接按绑定约束处理。经过求解可得出异形臂架的前6阶模态,振型如图2所示,对应的振型分析如表1所列。

表1 前6阶振型特征分析

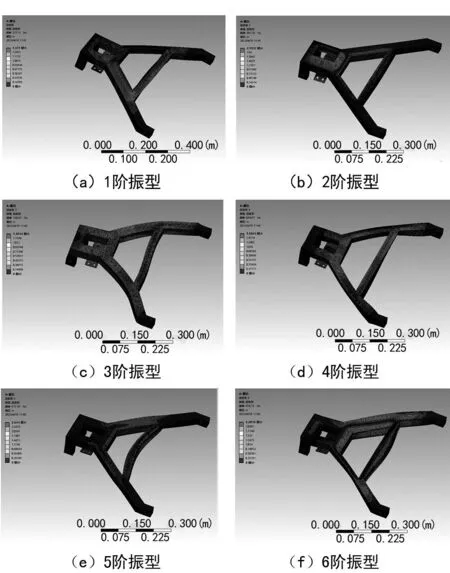
图2 前6阶模态振型图

根据前6阶振型及分析发现,异形臂架除刚体模态外,最小频率为371.12 Hz,最大频率为956.75 Hz,发生变形的位置均接近几何中心处,有摆动、扭转等变形。异形臂架刚度较好,模态频率较高。在设计类似臂架时,可考虑增加几何中心附近处的刚度、强度,这样效果会更好。

3 谐响应分析

3.1 谐响应分析理论

谐响应分析以模态分析为基础,通过谐响应分析可以确定部件、机构在承受正弦(简谐)规律变化的载荷时的稳态响应规律,可以反映出结构件在受到不同频率简谐载荷作用下自身的运动特性[1]。而异形臂架在工作模式下会受到来自车架的激振力、轮胎通过前车桥传递过来的激振力以及车架通过减震弹簧和液压缸传递过来的激振力作用。当这些激振力和异形臂架的频率一致或接近时,就会出现共振现象。这不仅会使悬架系统的振动噪声突增,影响关键零件、部件的寿命,还会影响到车辆行驶的平稳性。为了避免类似情况发生,有必要进行异形臂架的谐响应分析,以为异形臂架的性能优化提供依据。

结构在简谐载荷作用下的受迫振动的微分方程可表示为:

(5)

式中:{F}为简谐载荷的幅值向量;θ为激振力频率。

而节点位移响应为:

x={A}sin(θt-ψ)

(6)

式中:{A}为位移幅值向量;ψ为位移响应滞后激励载荷的相位角度。

将式(6)代入式(5),即可得到位移和频率之间的关系式,如式(7)所示。然后在有限元软件中设置异形臂架的频率范围和间隔,便可求解得到曲线的峰值频率[1]。

{A}=

(7)

3.2 谐响应分析结果

模态分析结果发现,异形臂架的固有频率范围在370～960 Hz。因此,此次谐响应分析所定义的频率范围为370～960 Hz,分析间隔为20 Hz。在异形臂架薄弱处添加激励力,幅值为 10 000 N,边界约束设定与模态分析一致,求解完毕后对零件进行频谱图提取。异形臂架是某型车悬架系统的关键结构件,其结构性能会影响悬架的性能,进而影响到整车的驾驶及行驶稳定性。根据模态分析前6阶振型,将力施加在异形臂架较薄弱的地方,对异形臂架x、y、z方向上的应力、变形频谱图进行提取,结果如图3～4所示。

图3 三个方向上的变形频谱图

图4 三个方向上的应力频谱图

对图3～4进行分析可以发现,应力、位移幅值基本出现在540 Hz、670 Hz、720 Hz附近,其主要峰值点主要集中在700 Hz附近,与模态分析中的第2阶以及第3阶的固有频率相近,该现象表明采用文中所用的模态以及谐响应分析方法是可靠的。

经过分析发现,就应力频谱图而言,异形臂架最大应力幅值均出现在y方向,该方向最大幅值出现在720 Hz。因此,该异形臂架在使用时应避免在720 Hz附近的激振力载荷下运行,整机工作频率不宜过高,以避免发生共振现象[2-4]。

4 结 论

文中以X型车的异形臂架进行振动特性分析,在对模型进行前处理的基础上依次进行了模态分析和谐响应分析,通过后处理,对计算结果及云图进行分析,所得结论如下。

(1) 经计算得出异形臂架有限元模型固有频率最小值为 371.12 Hz。异形臂架前段有前车桥、液压缸支撑,其后边两端和车架联结,因此,在高阶频率下,异形臂架容易出现摆动和扭转变形;根据前6阶振型可知,如想提高异形臂架的固有频率,可在异形臂架几何中心附近进行加强。

(2) 谐响应分析中,在370～960 Hz范围内且有激振力作用下,共振频率主要出现在异形臂架第2阶和第3阶固有频率附近,这表明仿真结果是合理的。由于应力、变形频谱图均在整机第1阶、第2阶、第3阶固有频率附近出现最大幅值,在实际运行中需要避免异形臂架在370 Hz、580 Hz、720 Hz附近以及更高频负载下进行工作,以防止发生共振。

(3) 因X型车属于重载,所以异形臂架的刚度、强度都要比较高,才能满足使用条件。而异形臂架自身的固有频率较高,需要较高的激励才会发生共振,且异形臂架有减震弹簧、液压缸等进行隔振,因此要使异形臂架不发生共振,可避开较为敏感的频率即可。文中研究结果可为后续同类型低速重载车辆设计提供一定的理论依据,也为异形臂架进一步优化减重提供理论依据。