低碳钢Q345多尺度疲劳断裂行为研究*

陈 鑫,童小龙,刘玉启,郭华泾

(1.湖南理工学院 土木建筑工程学院,湖南 岳阳 414006; 2.中原环保股份有限公司,河南 郑州 450000)

0 引 言

现如今,钢结构已经成为土木工程最重要的结构形式之一。而大多数钢结构失效是裂纹扩展引起的断裂,其结构服役周期远未达到其设计寿命。低碳钢Q345具有高强度、高韧性等优点,是最重要的钢结构制材之一[1-2]。含缺陷低碳钢Q345的疲劳断裂行为是钢结构失效研究的焦点,也是土木工程领域的前沿问题。

迄今为止,已经有不少学者基于断裂力学理论研究钢Q345的疲劳断裂行为。罗云蓉等[3]研究了Q345的低周疲劳性能,论证了其疲劳断裂是裂纹萌生与扩展引起的。刘刚等[4]基于能量等效原理和有限元方法提出了长条形试样小冲杆试验方法,并估算了Q345R钢的单轴本构关系。苏翰等[5]基于疲劳试验和显微技术研究了腐蚀环境下Q345qDNH钢的疲劳破坏机理,并分析了其对接焊缝疲劳性能。李明等[6]利用高周旋转弯曲疲劳试验分析了Q345FCA的疲劳断裂机理及其对接焊缝的高周疲劳性能。Dong等[7]结合疲劳试验数据研究了Q345低周疲劳裂纹扩展的机理,并建立了其疲劳断裂数理模型。Liao等[8]通过夏比冲击试验和疲劳试验研究了低温环境下Q345qD桥钢的疲劳裂纹扩展行为及其对接焊缝的疲劳性能。

断裂力学理论通常采用一条具有几何属性的主裂纹表征材料的受损状态,而忽略材料内部的微、细观缺陷,即认为存在主裂纹控制区,而其他区域仍然满足连续性和均匀性假设[9]。然而,相关研究表明[10-11],材料内部的微、细观缺陷是客观存在的,且这些微、细观缺陷的存在本身就是几何不连续性的,微、细观缺陷的萌生和扩展以及缺陷之间的相互作用等群体行为会较大程度地影响宏观裂纹附近的应力、应变场的分布。

尽管已有较多研究聚焦于Q345钢的疲劳断裂行为,但还是忽略了材料内部微、细观缺陷行为及其影响。因此,Q345钢的疲劳断裂问题仍未解决。笔者基于应力等效原理和有限元数值模拟技术,考虑材料内部微、细观缺陷对宏观裂纹的影响,模拟了带中心裂纹有限宽平板Q345钢的疲劳裂纹扩展过程,表征了考虑损伤的裂纹尖端场,并分析了其疲劳裂纹扩展行为。

1 疲劳损伤与断裂基本理论

根据断裂力学理论[9],应力强度因子K是表征弹性裂纹尖端场的断裂参量,对于I型裂纹,可以表示为:

(1)

式中:p为均布外荷载;F为修正系数。

根据Paris准则[12],疲劳裂纹扩展速率da/dN与应力强度因子幅值ΔK之间的关系为:

(2)

式中:C和m为材料常数。

J积分是描述弹塑性裂纹尖端的断裂参量,具有与路径无关等性质。对于任意一条按逆时针方向的曲线Γ,起始点和终止点分别为裂纹的下表面和上表面。J积分计算公式为:

(3)

式中:W为应变能密度(非线性);Ti代表在曲线Γ的弧度dΓ上的面力矢量;ui为该处的位移矢量。

裂纹尖端附近客观存在一定数量的微、细观缺陷,且微、细观缺陷的萌生和扩展行为会较大程度上影响宏观裂纹附近的应力、应变场的分布,导致宏观裂纹尖端存在塑性区,裂纹尖端构造如图1所示,图中①区和②区分别是损伤区和塑性区[13]。

图1 裂纹尖端构造图

根据损伤力学[14]可知,损伤是微、细观缺陷行为引起的结构性能的劣化。Miner准则是工程中使用最为广泛的损伤演化规律,其表征n次循环引起的损伤D的公式如下:

(4)

对于平面应力状态,考虑微、细观缺陷的影响,裂纹延长线(q=0)上塑性区半径R可以表示为[13]:

(5)

根据之前建立的应力等效原理[13]进行分析,即无损体在有效荷载作用下产生的应力等效于受损体在名义荷载作用下产生的应力,如图2所示。材料内部微、细观缺陷引起的损伤对宏观裂纹场的影响为:

(6)

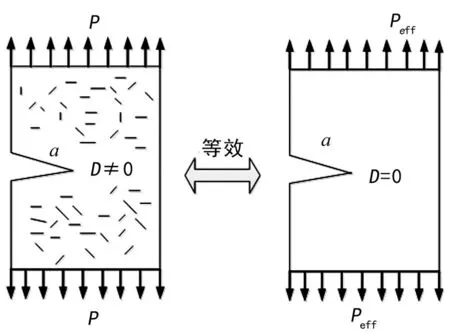
图2 应力等效原则

2 有限元数值模拟模型及其有效性验证

文中研究带中心裂纹的有限宽平板,其几何尺寸如图3所示,制材为Q345钢,屈服强度σs=345 MPa,泊松比μ=0.3,弹性模量E=206 GPa。平板承受单轴循环拉力,应力幅值σa=100 MPa,根据结构的对称性,利用有限元软件ABAQUS建立了1/4结构,假设初始裂纹a0=2 mm,有限元模型如图4所示,网格类型采用CPS8,结点总数为4 003,单元总数为1 284。

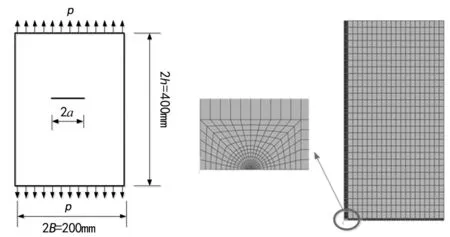
图3 带中心裂纹的有限宽平板

根据断裂力学[9],令p=100 MPa,将初始裂纹a0=2 mm带入计算公式(1),对应的应力强度因子修正系数F=1.002 5,则可得裂纹尖端应力强度因子KI=251.3 MPa.mm1/2;对应的数值模拟结果为KI=249.7 MPa.mm1/2,相对误差为0.6%,这说明此次研究建立的有限元模型是可靠的。

3 有限元数值模拟结果及其分析

文中采用Miner定律表征材料内部微、细观缺陷引起的损伤,基于应力等效原理将损伤引入裂纹扩展过程并进行多尺度有限元数值模拟,应力强度因子和J积分均可以直接从ABAQUS软件中提取。

3.1 裂纹尖端场分析

基于有限元数值模拟结果,分析裂纹扩展过程中的尖端塑性区和J积分变化规律。不同损伤程度下的裂纹尖端塑性区的分布云图、裂纹扩展过程中尖端J积分变化规律、裂纹延长线(q=0)上塑性区半径增长过程分别如图5～7所示。

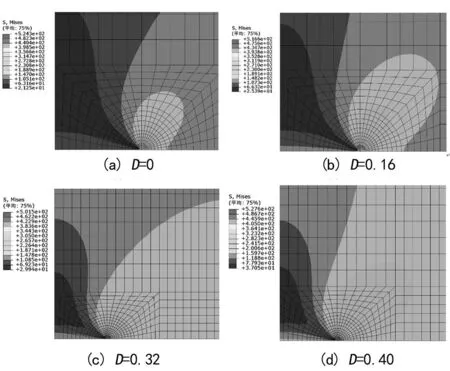
图5 裂纹尖端塑性区云图

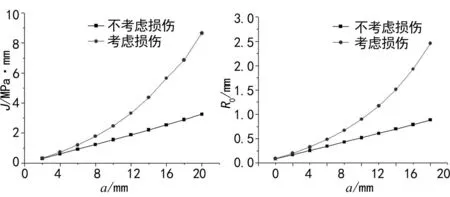
图6 裂纹尖端J积分变化图

由图5～7可得出如下结论。

(1) 随着材料内部损伤累积,裂纹尖端塑性区不断增长,说明材料内部微、细观缺陷对宏观裂纹尖端塑性区分布具有较大影响。

(2) 材料内部微、细观缺陷对宏观裂纹尖端的J积分的影响显著,且会导致其非线性增长。

(3) 宏观裂纹扩展过程中,材料内部的损伤对裂纹延长线(q=0)上塑性区的影响逐渐显著。

3.2 多尺度疲劳裂纹扩展分析

在小范围屈服条件下,K仍可以用于表征裂纹尖端场,文中采用Paris准则研究裂纹扩展行为,Q345钢的材料疲劳参数可取为[2]:C=1.3×10-13,m=2.2。结合数值模拟结果,裂纹扩展分析结果如图8、9所示。由图可得:在裂纹扩展过程中,结构内部微、细观缺陷引起的损伤会较大程度地影响裂纹尖端应力强度因子幅值变化,且较为明显地加速宏观裂纹扩展。

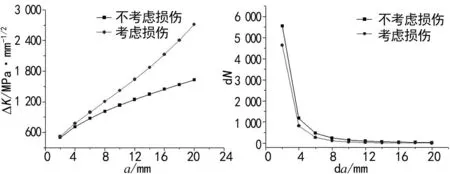
图8 应力强度因子幅值变化曲线

4 结 论

文章采用Miner准则表征材料内部微细观缺陷引起的损伤,进而利用ABAQUS建立考虑损伤的多尺度有限元模型,分析了含损伤的Q345钢疲劳断裂行为及其影响,得到以下主要结论。

(1) 材料内部微、细观缺陷引起的损伤对宏观裂纹尖端塑性区分布具有较大影响,且裂纹达到一定长度后,影响更为显著。

(2) 材料内部微、细观缺陷对宏观裂纹尖端的J积分的影响较为显著,且会导致其非线性增长。

(3) 在裂纹扩展过程中,材料内部微、细观缺陷引起的损伤会较大程度影响裂纹尖端应力强度因子幅值变化,且较为明显地加速宏观裂纹扩展。

通过文中的研究,可更好理解低碳钢Q345断裂机理及其断裂过程中裂纹尖端场特征,为Q345制材的钢结构疲劳断裂失效问题预防和诊断提供了理论基础,对于钢结构的广泛安全应用具有十分重要的战略性意义。