基于ANSYS的一种悬臂结构抗冲击优化设计*

王光越,张 炜

(1.中国船舶集团有限公司第七一〇研究所,湖北 宜昌 443003; 2.中国人民解放军92578部队,北京 100161)

0 引 言

目前,随着舰船领域的快速发展,船用设备的需求越来越多。船的设备中,悬臂结构的作用十分重要。悬臂结构通过焊接的方式固定在舰船的甲板上,在船体受到爆炸冲击时,悬臂结构会直接承受船体传过来的冲击力。因此,为避免设备损坏,需要对悬臂结构进行抗冲击仿真分析。

目前用于舰船设备的抗冲击分析方法包括动力学设计方法(DDAM)和时域分析法[1]。动力学设计方法是基于模态叠加的设计分析方法,它可以将设备简化为多个弹簧质量系统,通过对各阶模态解的合成得到设备的位移和应力,但此方式不能得到设备的瞬态响应。时域分析方法是通过一定的方法将冲击谱转换成加速度时间历程曲线并将其加载在设备上,此方法虽然计算时间较长,但能对设备在时域上进行瞬态分析,分析精度更高。基于此,笔者采用时域分析方法重点对设备上的悬臂结构进行抗冲击仿真分析[2-3],得到了悬臂结构各个部位的冲击应力云图;再通过对悬臂结构上的薄弱部位进行改进优化设计,使设备上的悬臂结构满足实际使用情况下的冲击性能要求。这对提升设备的环境适应性和增强设备的使用寿命具有实际效益,同时该分析结果对其它悬臂结构的抗冲击设计也具有一定的参考意义。

1 设计方案

悬臂结构主要功能是实现设备搭载,它主要由悬臂杆、支撑圆环、支撑底板和设备固定支架组成。悬臂结构上安装有设备A、设备B和设备C,整个悬臂结构通过螺钉固定在设备本体上,设备本体与基座相连固定在舰船的甲板上。悬臂结构材质采用不锈钢,该材质具有较好的防腐性能。通过UG建立悬臂结构的三维模型如图1所示。UG是机械工程常用的三维设计软件,具备模块丰富、操作简单等优点[4]。

图1 悬臂结构三维模型

2 冲击载荷分析设计

目前,冲击载荷多以三折线谱或冲击输入谱的形式来描述。三折线谱可以看做是冲击输入谱的图形表达形式。冲击输入谱主要包含等加速度谱、等速度谱和等位移谱三个参数。这三个参数描述了设备在不同频段的冲击载荷信息。冲击输入谱不可以直接作为载荷信息施加在设备上,需要通过一定的方式将输入谱信息转化为正负三角波或组合半正弦波的加速度信息。文章采用正负三角波对悬臂结构进行抗冲击性能分析。

对于设计初级阶段的设备而言,其冲击环境一般并不能完全明确。因此,在没有具体的冲击谱规定时,一般采用国军标GJB 1060.1 中的相关公式进行计算。文中设备抗冲击等级为A级,根据GJB 1060.1中水面舰艇用的设计值给定冲击方向上的冲击设计加速度。根据上述要求,不同方向冲击时,其设计值如表1所列,其中加速度和速度计算如式(1)、(2)所列。

(1)

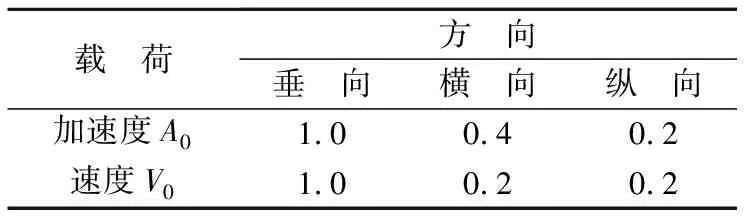
表1 甲板部位冲击输入表

(2)

根据德标BV043/85定义的正负三角波如图2所示。根据规定,第一个三角形的加速度峰值约为最大加速度A的3/5,第一个正三角形的面积约为最大速度V的3/4,第二个负三角形面积与第一个正三角形面积相等,此加速度历程经两次积分后得到位移,使t2=0.4t3,t4-t3=0.6(t5-t3)。

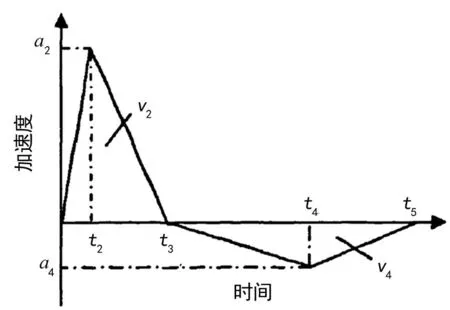
图2 三角波形输入

各主要参数计算为:

a2=0.6A

(3)

(4)

(5)

(6)

(7)

(8)

t4=t3+0.6(t5-t3)

(9)

根据已知设备重量,通过公式估算的方式得到设备冲击谱如表2所列。

表2 冲击输入谱

经过拟合计算可得垂向加速度函数如式(10)～(13)所列,拟合后的加速度时间历程曲线如图3所示。

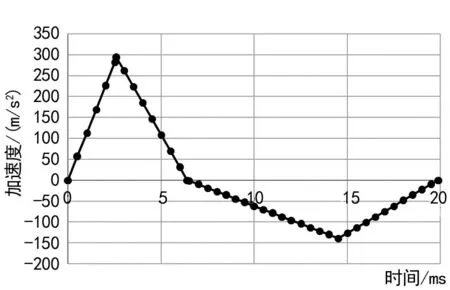
图3 加速度时间历程曲线

y=113.1×t(0≤t<2.6)

(10)

y=294-77.4×(t-2.6)(2.6≤t<6.4)

(11)

y=-17.2×(t-6.4)(6.4≤t<14.5)

(12)

y=-139.16+25.77×(t-14.5)(14.5≤t≤19.9)

(13)

3 抗冲击分析

3.1 分析方法

设备通过螺栓连接的方式固定在舰船甲板上,当舰船受到冲击时,冲击波通过船体传至设备。ANSYS是美国PTC公司开发的一款集强度分析、热分析、流体分析及电磁分析于一体的有限元分析软件,在机械行业中有着广泛的应用[5]。而ANSYS中的加速度载荷信息是整体加载在设备上,不符合实际受力情况。文章利用ANSYS中瞬态分析模块,根据牛顿第二定律,将加速度载荷信息转换为力的载荷信息,再将其施加在基础底面上,对悬臂结构进行抗冲击仿真分析,得到悬臂结构的各部位的应力情况。通过分析可知,垂向冲击载荷最恶劣,也是发生次数较多的方向,文章将根据垂向冲击的结果对悬臂结构进行优化设计。

3.2 网格划分

悬臂结构上设备A质量是15 kg,设备B质量是1.5 kg、设备C质量是2 kg。由于此次不对这些设备的冲击性能进行考核,因此将设备A、B、C以质量点的形式加载在悬臂结构的安装位置上。根据实际的装配关系,设置好各部件的接触类型,并将材料设置不锈钢,然后通过控制网格尺寸的方式对悬臂网格进行细化处理。细化后的整体结构一共划分210 777个网格单元。划分网格之后的设备的有限元模型如图4所示。

图4 网格模型

3.3 结构仿真

经过软件分析可知,整个设备质量为1 200 kg。根据牛顿第二定律F=ma,在设备的垂直方向上施加相关的位移约束和力学函数。仿真分析后的结果如图5、6所示。

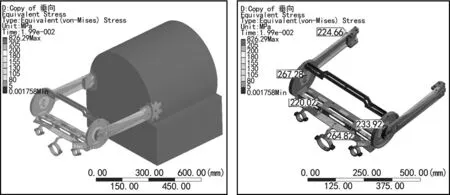
图5 垂向冲击应力云图图6 垂向冲击应力云图

从图5、6中可以看出,悬臂结构等效应力最大值为826.29 MPa,远远超出了材料的屈服极限。应力较大的部位包括悬臂杆的根部、支撑圆环的中心及支撑底板与设备支架连接的部位,这些部位的零件均需要进行结构加强处理。

3.4 结构优化

(1) 悬臂杆结构优化

从仿真结果可以看出,悬臂杆的最大应力集中在悬臂杆安装的根部,并且沿着悬臂杆长度方向逐渐减小。优化后的悬臂杆在原来两侧边加强筋的基础上增加一段长度240 mm、高度10 mm的加强筋;同时,在悬臂杆的根部设置宽度10 mm的竖筋,以增强整个悬臂杆的强度。优化前后的悬臂杆结构如图7所示。

图7 悬臂杆结构优化模型图8 支撑底板优化模型

(2) 支撑底板结构优化

支撑底板的超过不锈钢屈服应力的区域集中在底板平面上,呈大面积分布状态,因此底板强度需要整体加强。优化后的支撑底板将加强筋的数量由4个增加到11个,同时加强筋的厚度由3 mm增加到6 mm。优化前后的支撑底板结构如图8所示。

(3) 支撑圆环结构优化

支撑圆环的最大应力集中在圆心附近平面上,该平面中心通过转轴与悬臂杆连接。优化后的支撑圆环将圆板的厚度由3 mm增加到5 mm,以提升支撑圆环的整体强度。优化前后的支撑底板结构如图9所示。

图9 支撑圆环优化模型图10 优化后结构冲击应力云图

3.5 优化后结构仿真

将优化的模型导入到ANSYS中进行力学分析,仿真结果如图10所示。

从图10可以看出,经过优化后的悬臂结构等效应力最大值为202.64 MPa,低于材料的屈服极限,结构上的冲击应力明显下降,满足使用要求。

4 结 论

利用UG建立了悬臂结构的三维模型,利用德标BV043/85定义的正负三角波设计了悬臂结构的冲击加速度时间历程曲线,利用有限元分析软件ANSYS 对悬臂结构抗冲击强度进行了仿真分析,根据仿真分析结果对悬臂结构进行了优化设计,结论如下。

(1) 悬臂结构在垂向受到的冲击等效应力最大值为826.29 MPa,超过了材料的屈服极限,在冲击力的作用下是易损结构。

(2) 优化后悬臂结构仿真结果最大等效应力为202.6 MPa,结构优化有效,设备的抗冲击使用性能得到提升。