折臂式举高消防车臂架系统振动特性研究

李 　 圣，　滕 儒 民，　王 　 欣，　王 殿 龙*，　李 　 杰

( 1.大连理工大学 机械工程学院， 辽宁 大连　116024；2.大连益利亚工程机械有限公司， 辽宁 大连　116024 )



折臂式举高消防车臂架系统振动特性研究

李 圣1，滕 儒 民1，王 欣1，王 殿 龙*1，李 杰2

( 1.大连理工大学 机械工程学院， 辽宁 大连116024；2.大连益利亚工程机械有限公司， 辽宁 大连116024 )

举高消防车臂架系统多采用折叠臂形式，控制其末端平台工作过程中的动响应是提高举高消防车使用性能的重要途径，而臂架系统弯曲振动方程求解是研究此类问题的基础．为此，以百米级折臂式举高消防车臂架系统为研究对象，基于哈密顿原理推导了各节臂架的弯曲振动方程，并求解出了一号臂架和二号臂架前三阶振型函数挠度曲线及对应固有频率．通过实例在Simulink环境下模拟一号臂架和二号臂架在已知二号臂架仰角变化条件下的末端动挠度响应特性曲线，为大高度折臂式举高消防车末端平台振动抑制提供了理论准备．

折臂式；举高消防车；振动特性；动挠度

0　引　言

随着中高层及高层建筑越来越普遍，大高度举高消防车的市场需求呈上升趋势．百米级举高消防车为确保其整车尺寸满足道路通行条件，其臂架系统多采用折臂形式．因而，控制臂架末端平台的动响应是提升举高消防车使用性能的重要途径．

针对折臂式臂架系统，国内外学者研究了其运动学以及动力学特性．例如运用拉格朗日方程建立了高空作业车折臂式臂架系统的动力学方程并进行了数值仿真[1]；分析了折臂式举高消防车臂架系统的末端速度，为折臂式臂架系统的运动学分析提供了参考[2-5]．Kharitonov等在直臂式云梯消防车臂架系统的主动减振控制方面有着深入的研究并取得了显著的成果，为实现举高消防车主动减振提供了重要的参考[6-7]．柔性机器人双连杆机械臂动力学方面的研究和折叠式举高消防车臂架系统振动特性的分析具有相通的方法，该领域的学者或采用拉格朗日方程和假设模态方法对机械手臂进行动力学建模；或基于哈密顿原理推导其动力学模型，利用自适应边界条件控制方法实现了对双连杆柔性臂架末端的控制[8-10]．本文通过推导折臂式举高消防车臂架系统一号臂架和二号臂架的振动特性方程，并使用仿真软件Simulink 对一号臂架和二号臂架末端动挠度进行计算仿真．

1　臂架系统的弯曲振动模型

本文研究的折臂式举高消防车臂架系统主要包括由6级伸缩臂组成的一号臂架、由末端工作平台和3级伸缩臂组成的二号臂架，以及各节臂架的变幅油缸三部分．如图1所示，变幅油缸1分别铰接于一号臂架和底盘，变幅油缸2分别铰接于一号臂架和二号臂架．臂架全伸工况时，一号臂架不进行变幅动作．本文研究的重点在于分析一号臂架与二号臂架之间的耦合关系并得到各节臂架的弯曲振动特性方程，将一号臂架和二号臂架考虑成等截面的欧拉-伯努利梁．

运用混合坐标建模方法中的切线法，建立臂架系统简化模型(图2)．X0、Y0为笛卡尔坐标系；坐标轴X1相切于一号臂架根部，坐标轴X2相切于二号臂架根部，坐标轴X3平行于坐标轴X1．

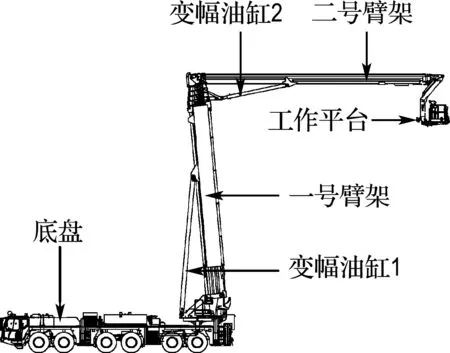
图1　折臂式举高消防车结构形式

图2　臂架系统简化模型

一号臂架在工作时不作变幅运动，折臂式臂架系统作如下简化：变幅油缸1和2连同对应的根部铰点简化为具有转动惯量的驱动轮毂O1、O2．由于铰点位置为简化的驱动轮毂，一号臂架可简化为根部固支在驱动轮毂O1上的等截面悬臂梁L1，二号臂架可简化为带有末端质量块M的根部固支在驱动轮毂O2上的等截面悬臂梁L2．轮毂O2处变幅油缸2的等效转动惯量为J2，作用力矩为M2，二号臂架末端质量块等效转动惯量为Je．文中所涉及的其他参数为Li：各节臂架长度；ρAi：各节臂架线密度；EIi：各节臂架抗弯当量刚度；θ1：坐标轴X1与坐标轴X0的夹角；θ2：坐标轴X2与坐标轴X3的夹角；w1：一号臂架的挠度；w2：二号臂架的挠度；w′：臂架挠度对臂架轴线方向的导数．

根据哈密顿原理[11]和简化后臂架系统模型，有

(1)

式中：T为臂架系统的动能，V为臂架系统的势能，W为臂架系统非有势力的虚功．且

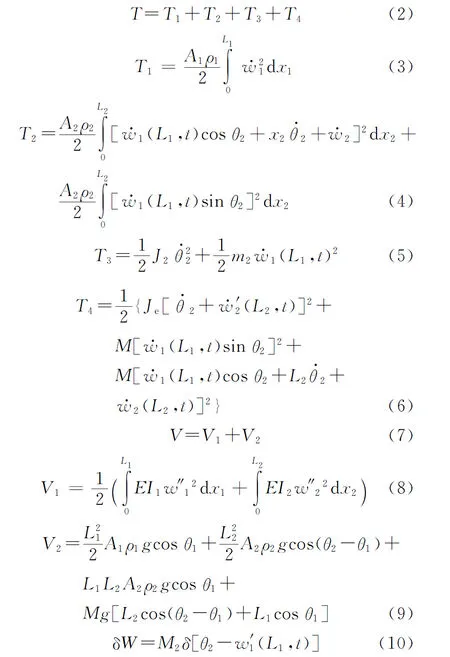
式中：T1为一号臂架的动能，T2为二号臂架的动能，T3为驱动轮毂O2的动能，T4为二号臂架末端平台的动能；V1为臂架系统的弹性势能，V2为臂架系统的重力势能；δW为系统非有势力做功的变分处理．将方程(2)～(10)代入系统方程(1)中，进行变分以及积分处理，得到系统偏微分方程(11)、(12)以及对应的边界条件(13)～(18)．

式(11)～(20)为两节柔性折臂式臂架系统的振动微分方程．根据系统偏微分方程(11)、(12)与边界条件(13)～(20)，两节臂架之间存在着明显的柔性耦合关系，即一号臂架的末端响应影响着二号臂架的系统偏微分方程(12)与二号臂架的边界条件(15)、(17)、(18)，二号臂架影响着一号臂架的边界条件(13)．由于二号臂架并未影响到一号臂架的系统偏微分方程，暂时不考虑二号臂架动挠度，可以先求解出一号臂架的振动特性方程，进而求得二号臂架的振动特性方程．

2　一号臂架振动特性方程

两节臂架全伸工况时，一号臂架固定于某一角度不作变幅运动而将其简化成根部固接的悬臂梁模型．根据系统边界条件(18)，二号臂架对一号臂架末端的激励作用为力矩M2，为求解方便将其转化为变幅油缸2对一号臂架的作用力F，有

(21)

(22)

式(22)中，l为一号臂架末端铰点至变幅油缸2的垂线距离．根据一号臂架的系统偏微分方程(11)，一号臂架弯曲振动具有与时间无关的确定振型的特性，采用分离变量的方式对其进行求解．并且通解的形式可以表示为

(23)

式中：Y1r(x1)是一号臂架弯曲振动方程关于空间解的函数，T1r(t)是其关于时间解的函数．把式(23)代入一号臂架的系统偏微分方程(11)中可以得到

(24)

(25)

关于空间解的函数Y1r(x1)，其具体形式为

Y1r(x1)=C1sinβ1rx1+C2cosβ1rx1+C3shβ1rx1+C4chβ1rx1

(26)

C2=-C4，C1=-C3

(27)

(shβ1rL1+sinβ1rL1)C3+

(chβ1rL1+cosβ1rL1)C4=0，

(chβ1rL1+cosβ1rL1)C3+

(shβ1rL1-sinβ1rL1)C4=0

(28)

式(28)有解的条件是

(29)

上述方程属于超越方程，无法求出解析解，运用Matlab作出方程(29)的图形并且对其寻根以精确得出其关于β1rL1的前三阶根，分别为1.895、4.694、7.855，一号臂架各阶振型函数为

Y1r(x1)=chβ1rx1-cosβ1rx1+ξ1r(shβ1rx1-sinβ1rx1)

(30)

(31)

一号臂架末端受激励F的作用时系统运动偏微分方程可以表示为

(32)

上述方程第r个主坐标系下的运动微分方程可以表示为

T 551r(t)+2μ1rT.1r(t)+μ21rT1r(t)=F*1r(t)M1r

(33)

(34)

(35)

综合式(26)、(33)可以求得一号臂架受末端激励作用下振动特性方程的解为

(36)

3　二号臂架振动特性方程

根据系统方程(12)，二号臂架含有一号臂架挠度的耦合项，而这一部分的耦合项根据方程(36)可以求出．令

R(x2，t)=x2θ2+w2(x2，t)+

∫t0[w.1(L1,ξ)cosθ2]dξ

(37)

则方程(37)满足二号臂架的系统偏微分方程(12)以及二号臂架的系统边界条件(14)～(18)，重新整理二号臂架系统偏微分方程以及边界条件得

变幅油缸2及其动力学响应在本文研究中不做考虑，且把二号臂架的仰角u(t)=θ2(t)作为系统的输入．

3.1通解分解

根据重新整理的方程(38)～(42)，可知二号臂架弯曲振动的边界条件使得二号臂架弯曲振动微分方程不再是齐次方程组．文献[12]求解高空作业车直臂系统振动微分方程的思路对本文二号臂架振动特性方程求解具有重要的借鉴意义．针对二号臂架振动特性方程组，其解可以考虑成齐次部分Rh以及非齐次部分Ri的和．即

R(x2，t)=Rh(x2，t)+Ri(x2，t)

(43)

其中Ri(x2，t)符合二号臂架系统的非齐次边界条件(39)～(42)，Rh(x2，t)需要满足系统偏微分方程(38)．

3.2非齐次边界条件求解

令Ri(x2，t)=f(x2)u(t)，u(t)=θ2(t)，则有

(44)

把上式代入系统边界条件(39)、(40)中有

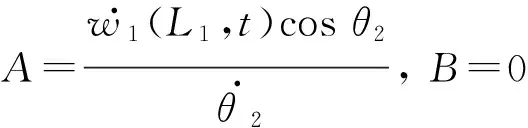
A=w.1(L1,t)cosθ2θ.2,B=0

(45)

考虑到二号臂架弯曲振动方程非齐次解的可行性以及在后期方程处理时迭代方法的使用，此时A作为常数项处理．把式(44)代入式(41)、(42)中：

(46)

将方程组的通解代入系统偏微分方程(38)以及边界条件(39)～(42)中可以得到

(47)

Rh(0，t)=R′h(0，t)=0

(48)

(49)

(50)

3.3齐次方程组部分求解

二号臂架齐次方程组的解描述为

(51)

二号臂架振动方程空间解与时间解的形式为

Y2r(x)=C1sinβ2rx2+C2cosβ2rx2+C3shβ2rx2+C4chβ2rx2

(52)

(53)

把二号臂架振动方程的解(51)代入系统边界条件(47)～(50)中可以得到

Y2r(0)=0，Y′2r(0)=0

(54)

(55)

(56)

二号臂架关于空间的解(52)代入边界条件(54)中可以求得C2=-C4，C1=-C3，且有

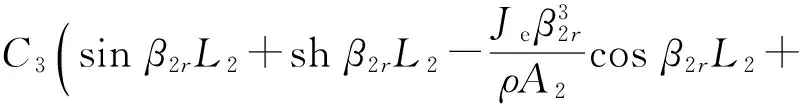
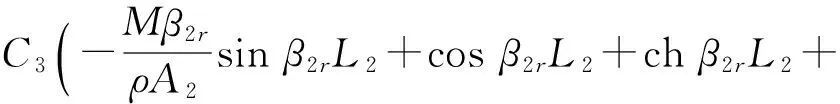
(57)

运用Matlab绘制上述超越方程组(57)的图形并寻根，可以得到关于β2rL2前三阶根的精确解分别为1.703、4.615、8.015，且二号臂架系统的振型函数可以表示为

Y2r(x2)=chβ2rx2-cosβ2rx2+ξ2r(shβ2rx2-sinβ2rx2)

(58)

(59)

3.4主坐标下二号臂架振动特性方程的表达

3.4.1二号臂架振型函数正交性关系为了使二号臂架振动微分方程解耦，需要找到二号臂架振型函数特有的正交性关系．对于不同阶数的振型函数Y2r(x1)和Y2s(x1)，对应阶数下的固有频率为w2r和w2s．根据方程(46)可知

(60)

分别用Y2s(x1)和Y2r(x1)乘以上述方程组的两端，同时在二号臂架全长上积分处理，之后两方程相减可以得到

(61)

由于w2r≠w2s，有

(62)

二号臂架的振型函数关于上式具有正交性．

3.4.2主坐标系下振动微分方程的表示根据3.4.1节证明的振型函数正交性的形式(62)，对于任意函数q1(x)和q2(x)，定义

〈q1(z)，q2(z)〉=Mq1(L2)q2(L2)-Jeq′1(L2)q′2(L2)+

(63)

(64)

二号臂架系统各个位置的动位移可以表示为主坐标平面内的振型函数与权函数的乘积．根据方程(63)和(64)可以定义任意函数广义傅里叶级数的展开形式如下：

(65)

(66)

把二号臂架振动微分方程通解在主坐标形式下进行傅里叶展开可得

(67)

对上式进一步整理，可以得到二号臂架振动微分通解时间函数的第r项的展开形式：

(68)

二号臂架振动微分方程的通解以及二号臂架的动挠度可以表示为

(69)

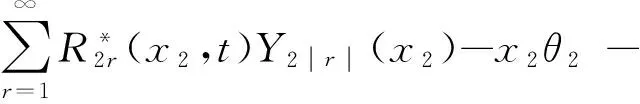
∫t0[w.1(L1,ξ)cosθ2]dξ

(70)

3.5二号臂架振动特性方程状态空间表述形式

针对3.4.2节得出的二号臂架振动微分方程(69)与动挠度方程(70)，借助软件Simulink中状态空间模块对二号臂架振动特性进行仿真．第一阶振型函数对整个振型函数起主导作用，现只考虑二号臂架弯曲振动方程的前两阶振型函数．令x=(x1x2x3x4)，并且

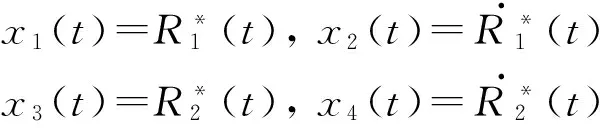
x1(t)=R*1(t),x2(t)=R.*1(t)x3(t)=R*2(t),x4(t)=R.*2(t)

(71)

由振动微分方程解(69)的方程形式，可以构造如下形式的状态空间方程：

x.=A·x+B·uy=C·x+D·u

(72)

(73)

(74)

式(73)中的κi为二号臂架的阻尼系数．根据不同需求的输出，矩阵C、D取不同的值，为了得到二号臂架根部的位移，C、D取以下值：

(75)

4　实际算例

本文以某一型号110 m举高消防车臂架实际结构为研究对象，利用前文所得一、二号臂架振动特性方程进行实际算例的求解计算．其中，一、二号臂架结构的具体截面形状如图3(a)、(b)所示．

一号臂架和二号臂架长度及截面属性、二号臂架末端作业平台和简化轮毂O2处的具体参数见表1．其中，作业平台质量为平台自身质量；一号臂架末端转动惯量为简化轮毂O2的转动惯量；二号臂架末端转动惯量为工作平台相对二号臂架末端的转动惯量．

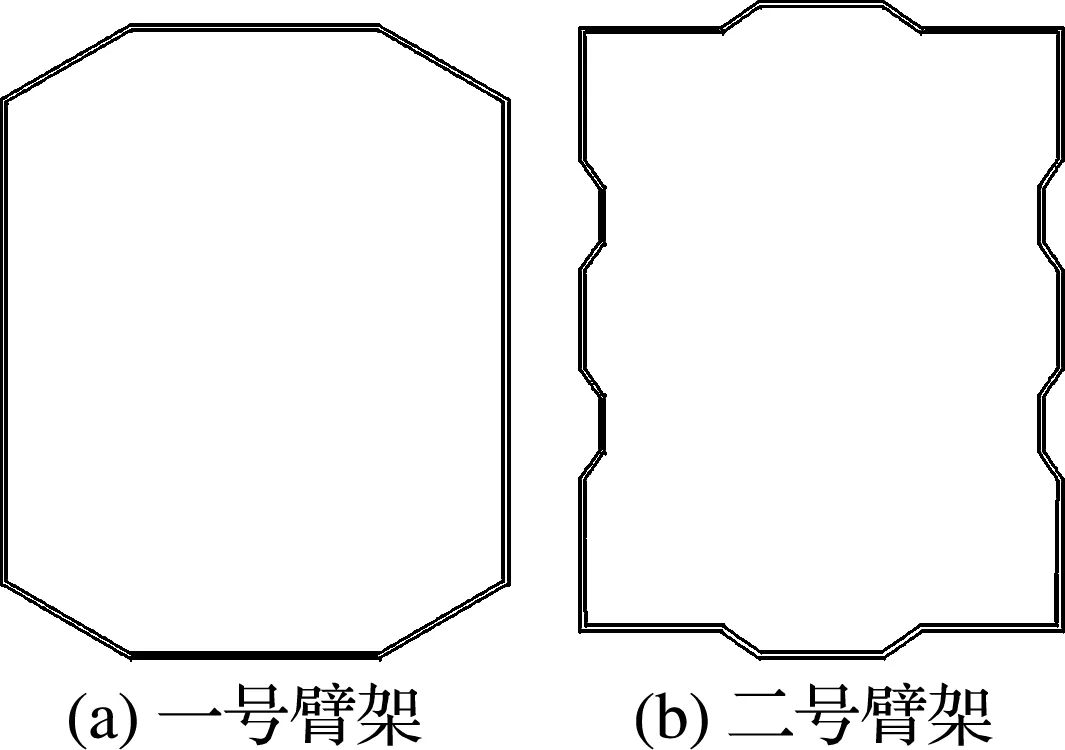
图3　一号和二号臂架截面

表1　臂架系统参数

将表1中具体参数代入各节臂架弯曲振动特性方程(30)、(58)，借助Matlab可以得到一号、二号臂架的前三阶归一化振型函数曲线，分别如图4和图5所示．

通常低阶振型对臂架结构动态特性的影响较大，取一号臂架的前三阶振型函数及固有频率、二号臂架的前两阶振型函数及固有频率．图6空白处为举高消防车实际的作业区间，位置2至5是举高消防车主要的高空作业区间．

分析一号臂架位置对一号臂架和二号臂架末端动挠度的影响，一号臂架选择如图7所示的3种位置，即θ1为5°、15°和25°；对于3种不同位置的一号臂架，θ2变化一致并且如图8所示，其中θ2的0°对应于图6中位置1；27°对应于位置2；73°对应于位置3．

图4　归一化的一号臂架前三阶振型函数

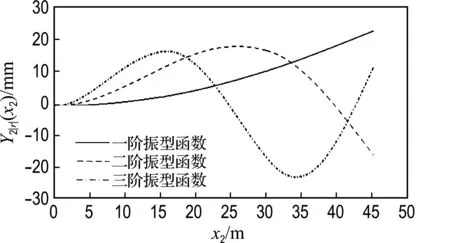
图5　归一化的二号臂架前三阶振型函数

图6　臂架作业区间

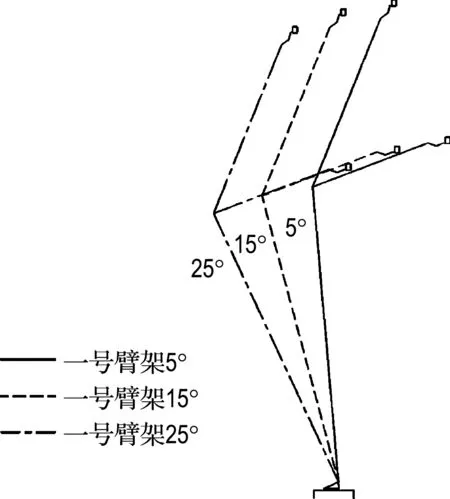
图7　一号臂架角位置

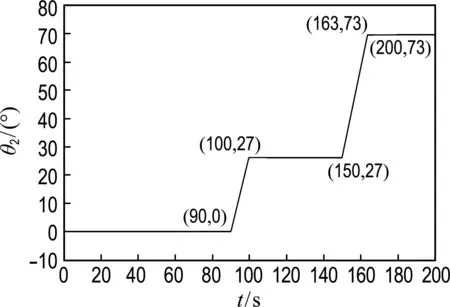
图8　二号臂架角度变化曲线1

图9中，仿真初期一号臂架处于自由振动状态，一号臂架末端振动稳定之后其动挠度随着θ2增大而增大；随着θ1增大，其末端动挠度在自由振动阶段幅值增大，而之后动挠度出现减小的趋势；图10为二号臂架末端动挠度，其在二号臂架启、制动时存在剧烈高频振动现象；随着θ1值逐步增大，末端动挠度减小．

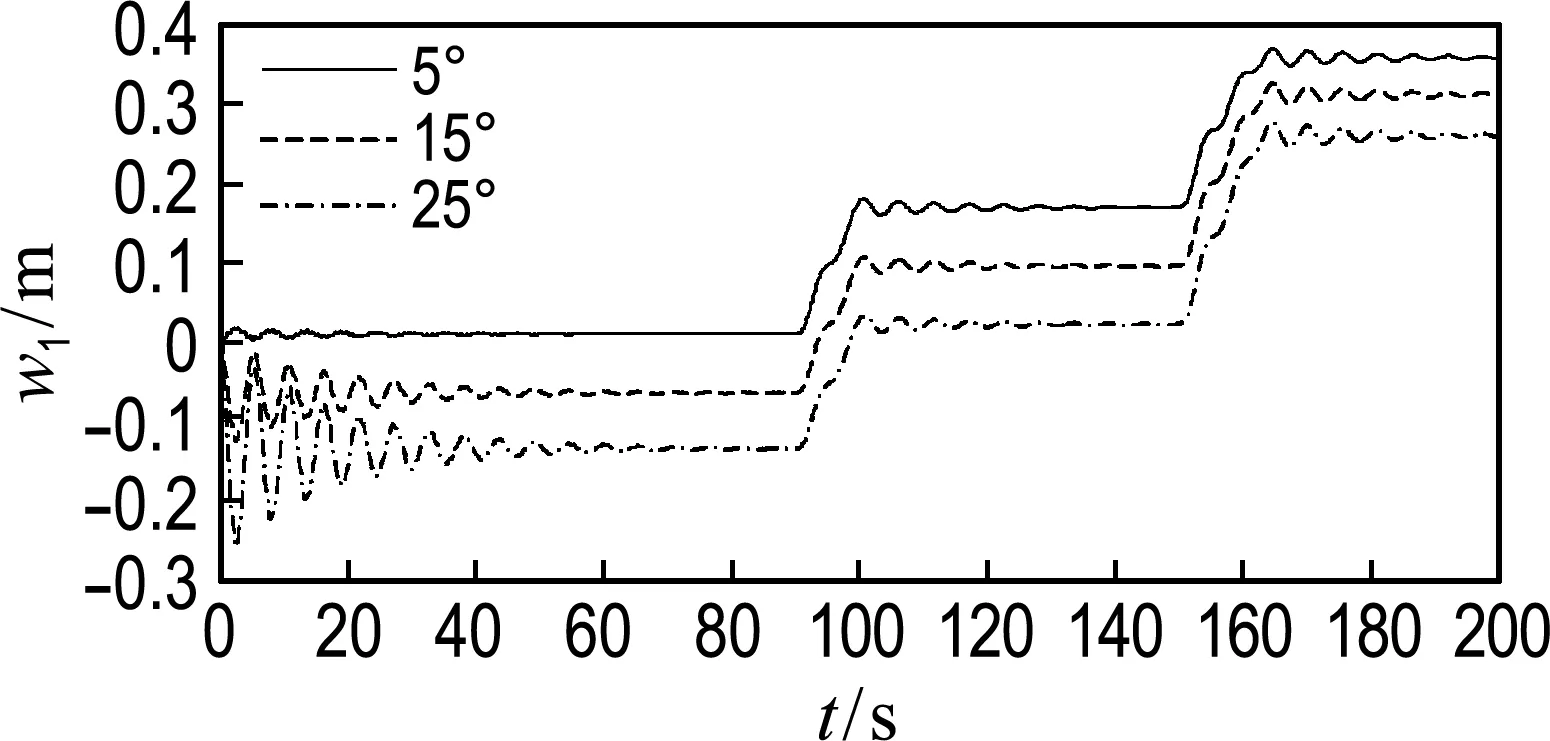
图9　一号臂架末端动挠度1

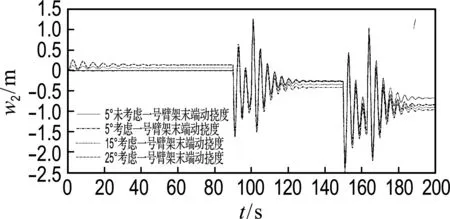
图10　二号臂架末端动挠度1

现分析二号臂架在不同作业区间对一号臂架和二号臂架末端动挠度的影响，θ1固定在5°，θ2的变化如图11中信号1和信号2所示．也即选择图6中二号臂架作业区间2-3和作业区间4-5进行对比．

根据图12，当二号臂架在图6中位置4，也即水平位置时，其对一号臂架力矩的作用达到最大值；二号臂架从水平位置继续向下运动后，一号臂架的动挠度逐渐减小．图13中，信号1和信号2中二号臂架同时进行变幅运动，因此二号臂架的动挠度变化一致；并且，二号臂架在输入信号2下，也即图6中区间4-5作业时，其末端动挠度增大，且其振动相对信号1更加剧烈．

图11　二号臂架角度变化曲线2

图12　一号臂架末端动挠度2

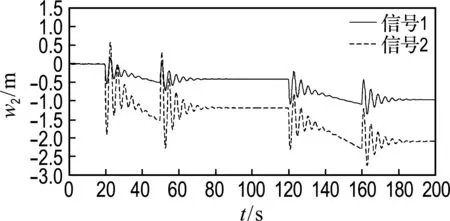
图13　二号臂架末端动挠度2

5　结　语

本文基于哈密顿原理，推导了二号臂架具有末端质量的折叠式举高消防车臂架系统的弯曲振动微分方程，得出了某型号百米级折臂式举高消防车一号臂架以及二号臂架的前三阶固有频率和对应的振型函数．根据一号臂架和二号臂架末端的振动特性方程，利用软件Simulink仿真得到了已知二号臂架仰角变化条件下一号臂架和二号臂架末端动挠度响应特性曲线；对比分析了一号臂架和二号臂架在不同的区间作业对一号臂架和二号臂架末端动挠度的影响．上述研究为实现折臂式举高消防车臂架系统振动主动控制提供了理论准备．

[1]蒙树立,熊静琪,吕志刚. 折叠式高空作业车臂架系统的动力学建模[J]. 噪声与振动控制, 2012, 32(4):63-67.

MENG Shu-li, XIONG Jing-qi, LV Zhi-gang. Modeling of arm system of folding-boom aerial platform vehicle [J]. Noise and Vibration Control, 2012, 32(4):63-67. (in Chinese)

[2]石鹏飞,周小辉,夏益民. 举高类消防车折叠臂架机构运动分析[J]. 建筑机械, 2015(1):70-77.

SHI Peng-fei, ZHOU Xiao-hui, XIA Yi-min. Motion analysis on boom system of fire truck for high-class [J]. Construction Machinery, 2015(1):70-77. (in Chinese)

[3]高 云,李建涛,张 涛,等. 混凝土泵车操纵性特性研究[J]. 中国工程机械学报, 2012, 10(3):369-373.

GAO Yun, LI Jian-tao, ZHANG Tao,etal. Controllability study on concrete pump trucks [J]. Chinese Journal of Construction Machinery, 2012, 10(3):369-373. (in Chinese)

[4]滕儒民,屈福政,张志刚,等. 高空作业车轨迹控制设计研究[J]. 大连理工大学学报, 2012, 52(4):522-528.

TENG Ru-min, QU Fu-zheng, ZHANG Zhi-gang,etal. Study of control trajectory design for aerial working platform vehicle [J]. Journal of Dalian University of Technology, 2012, 52(4):522-528. (in Chinese)

[5]杨 萍. 冲击载荷作用下登高平台消防车动态响应研究[D]. 大连:大连理工大学, 2012.

YANG Ping. Research on dynamic response of aerial platform fire truck under impact load [D]. Dalian:Dalian University of Technology, 2012. (in Chinese)

[6]Kharitonov A, Zimmert N, Sawodny O. Active oscillation damping of the fire-rescue turntable ladder [C] // Proceedings of the IEEE Conference on Control Applications 2007. Singapore City:IEEE, 2007.

[7]Zimmert N, Pertsch A, Sawodny O. 2-DOF control of a fire-rescue turntable ladder [J]. IEEE Transactions on Control Systems Technology, 2012, 20(2):438-452.

[8]谭珍珍,张 泉,刘伟健. 双柔性臂机器人的建模和主动振动控制[J]. 机械制造与自动化, 2014, 43(1):166-170.

TAN Zhen-zhen, ZHANG Quan, LIU Wei-jian. Dynamic modeling and active vibration control of two cooperating flexible robotic manipulator [J]. Machine Building & Automation, 2014, 43(1):166-170. (in Chinese)

[9]Zhang X P, Xu W W, Nair S S,etal. PDE modeling and control of a flexible two-link manipulator [J]. IEEE Transactions on Control Systems Technology, 2005, 13(2):301-312.

[10]ZHANG Lin-jun, LIU Jin-kun. Adaptive boundary control for flexible two-link manipulator based on partial differential equation dynamic model [J]. IET Control Theory and Applications, 2013, 7(1):43-51.

[11]谢官模. 振动力学[M]. 北京:国防工业出版社, 2011.

XIE Guan-mo. Vibration Mechanics [M]. Beijing:National Defense University Press, 2011. (in Chinese)

[12]高凌翀. 高空作业车直臂系统振动抑制研究 [D]. 大连:大连理工大学, 2015.

GAO Ling-chong. Study on vibration suppression for telescopic boom system of aerial work vehicle [D]. Dalian:Dalian University of Technology, 2015. (in Chinese)

Research on vibration characteristics of folding boom system for aerial work fire-truck

LISheng1,TENGRu-min1,WANGXin1,WANGDian-long*1,LIJie2

( 1.School of Mechanical Engineering, Dalian University of Technology, Dalian 116024, China；2.Dalian YILIYA Construction Machinery Co., Ltd., Dalian 116024, China )

The folding boom is widely used in aerial work fire-trucks (AWFs). In order to improve AWFs′ working performance, an important way is to control the dynamic response of the tip platform during operation, whose foundation is how to solve the bending vibration equation of the boom system. As an example of folding boom system of 110 m AWF, the bending vibration equations for each boom are established, and then, the first three-order deflections curves of vibration shape function and corresponding natural frequencies of the first and second booms are obtained by the Hamilton principle. According to the elevation angle of the second boom, response curves of the dynamic deflections of the first and second booms tip are simulated in Simulink with this actual case. This study provides theoretical preparation for vibration control of AWFs tip platform.

folding boom; aerial work fire-trucks (AWFs); vibration characteristics; dynamic deflection

1000-8608(2016)05-0457-09

2016-01-15；

2016-08-01．

国家自然科学基金资助项目(51475068).

李 圣(1991-)，男，硕士生，E-mail:lisheng_good@163.com；王殿龙*(1962-)，男，教授，博士生导师，E-mail:dlwang@dlut.edu.cn.

O326；TH113

A

10.7511/dllgxb201605004