基于混合协作NOMA的安全MEC能耗优化

余雪勇, 傅新程, 朱洪波

(1. 南京邮电大学江苏省无线通信重点实验室, 江苏 南京 210003;2. 南京邮电大学教育部泛在网络健康服务系统工程研究中心, 江苏 南京 210003)

0 引 言

随着网络信息时代的发展,人们对数据的处理和网络性能的提高提出了越来越高的要求。在物联网场景中,移动边缘计算(mobile edge computing,MEC)能够有效地解决计算延迟和网络拥塞问题。计算卸载是大多数利用MEC的用户的主要方式[1]。MEC通过边缘云的计算和存储资源为用户提供计算能力,解决了计算能力不足的问题[2]。而无线通信的广播性质可能会在卸载过程中将用户的隐私数据泄露给未经授权的窃听者[3]。此外,无线卸载功能使得许多现有的传统有线云计算系统的隐私保护技术效果较差。如果没有适当的保护机制,对隐私敏感的用户可能不会使用MEC[4]。同时,处理大量数据以及卸载过程中需要对数据传输的安全进行保障所花费的额外能耗是不可忽视的[5]。如何在安全传输中尽量降低系统能耗是研究中不可忽视的问题之一。

对于上述MEC中卸载隐私的问题,现有机制大多仍依赖于加密技术[6],但是这些机制并不是完全安全的,随着科技的进步,解密的代价将进一步降低。相比之下,可以从文献[7]中对于以信息论为基础的物理层安全中找到答案,这被认为是以更低的计算成本提供更强的隐私概念。实际上,在过去的几十年里,为了提高传统无线通信系统的安全性和私密性,人们对物理层安全技术(如人工噪声和接收端干扰[8])进行了广泛的研究。除了上层加密算法之外,物理层安全利用基于信道物理特性的窃听编码,可以提供完美的信息安全,而无需事先生成和分发密钥[9]。此外,非正交多址接入(non-orthogonal multiple access,NOMA)是第5代(fifth-generation,5G)无线网络实现低延迟、大规模连接和高吞吐量的关键技术。NOMA的关键思想是为同一资源块中的多个用户提供服务并可以集成到现有和未来的无线系统中,通过同时分配多个无线传输来进一步提高频谱效率[10]。

最近,针对上述技术结合的想法与实践越来越多。Yang等[11]提到在边缘计算卸载任务过程中,物理层安全是保证卸载数据安全传输的有效技术。He等[12]通过对窃听者解码过程的分析发现主动释放的干扰信号可以对窃听者的解码产生干扰,从而保证信息的安全传输。而Wu等[13]则考虑了一个实际的被动窃听场景,在保密中断概率和计算延迟的约束下导出了最优解半封闭表达式,并在安全卸载率、计算延迟和保密中断概率有限的情况下,实现了用户权重和能耗最小化问题。而Pan等[14]采用了NOMA功率复用技术,通过优化传输功率、传输时间分配和任务分配分区,实现多用户连接,最大限度地降低总能耗。文献[15]巧妙利用了NOMA用户对之间的协作来提高安全性。该方案利用保密中断概率和保密计算概率来衡量安全性能并列出了基本表达式。文献[16]在此基础上增加了安全速率约束问题,并提出一种基于差分凸算法来解决问题,同时还提出了低复杂度的KKT(Karush-Kuhn-Tucker)条件算法作比较,在一系列约束的情况下得到系统能耗的最优值。随着5G技术的逐渐普及,2019年,Lin等[17]研究了NOMA使MEC网络具有物理层安全性,并通过优化传输功率和中央处理器频率来优化资源分配,最终实现安全计算效率的最大化。在文献[18]中提出一种新的MEC系统的计算和通信用户协作方法,通过分割时间槽,在不同的时隙中进行不同的任务以提高延迟约束计算的能量效率。在现有的资料中,上行NOMA-MEC的优势已经在节能[19]、减小时延[20]和提高计算成功概率[21]等方面得到了证明,是未来通信发展中不可或缺的一项技术。

从以上讨论中可以看出,在物联网场景中对窃听者的防窃听手段大都采用自然噪声干扰以及合法中继干扰手段,从而忽视了互干扰的利用。并且,对于时隙动态分配更加丰富和智能的今天,利用NOMA的特性对用户多时隙能耗优化问题并没有得到研究。此外,同一个时隙下用户存在协作形式单一,参与协作的用户自身需要处理的数据量和效率不同以及对于系统的保密性能提升不明显等问题。鉴于此,本文在NOMA的边缘卸载场景中,围绕着部分卸载边缘计算的问题,通过改变模型和用户的协作模式,提出了一种在保证安全隐私前提下的多时隙系统能耗优化方案。在第1个时隙中通过用户卸载的互干扰来扰乱窃听者,第2个时隙则取消不包含信息量的干扰功率,将剩余数据量转成更为安全的本地计算进行处理。本文的主要贡献总结如下:

(1) 首先,考虑到每个用户对于时延的要求不同,提出了一种基于NOMA的多时隙混合协作方案。系统根据用户即时需要处理的数据量将处理时间通过比例参数动态划分为两个时隙。在第一个时隙里,用户通过卸载计算时的混合功率来干扰窃听者的同时保证信息安全;而任务数据量较多的用户在下一时隙,将无法按时计算处理的数据量转为本地计算。由此,减少配对用户终端因发送无信息的干扰信号而额外产生的能耗,并保护了信息隐私。

(2) 其次,在考虑用户优先级和保密度的前提下推导出了保密中断概率的闭合表达式,并提出了一个优化问题,使得系统用户在保证隐私的前提下实现能耗的最小化。

(3) 为了求解非凸优化问题,将其分解为3个子问题:① 数据量和卸载功率指标优化以及资源分配。② 数据量处理比例优化。③ 时隙分配比例优化。并通过块坐标下降算法循环迭代来联合求解这3个子问题。

(4) 最后,提出多时隙混合协作(multi-slot hybrid collaboration, MSHC)方案,仿真结果表明,与其他方案相比,该方案具有更大的优越性,可以进一步降低系统的能耗,同时也为NOMA未来的普及提供了新的思路。

1 系统模型

上行NOMA中边缘计算能耗优化及物理层安全隐私研究系统图如图1所示。此系统由k(k>1)个用户终端、1个窃听者、1台与基站相连的边缘服务器组成。所有的终端节点都配备了一根天线,而无线信道采用了非选择性准静态块衰落模型[22],使信道在给定传输时间T内保持不变。其中,用户终端数据处理采用部分卸载的方式,即一部分由本地处理,剩余部分卸载到边缘服务器进行处理。

图1 NOMA辅助的多用户安全卸载MEC系统Fig.1 NOMA-assisted multi-user secure offloading MEC system

由于NOMA的特性,系统会受到强干扰限制,虽然串行干扰消除(successive interference cancellation, SIC)可以用来抑制多用户NOMA的干扰,但当大量用户执行NOMA时,会对移动终端的硬件复杂度有很高的要求。此外,由于移动终端的干扰负担更重,信号处理延迟将进一步增加。因此,多用户NOMA方案的研究可以通过将两个用户分组在一起,并使用用户配对技术联合执行NOMA来完成[23]。此外,配对的两个用户在卸载的过程中,卸载信号的叠加会给窃听者造成干扰,有效地提高了NOMA系统的安全性,从而保证用户的隐私不被窃听。因此,在不失一般性的前提下,可以只关注两个用户的简化模型。通过信道状态条件来设置一个强用户和一个弱用户进行配对,分别命名为st和w。在用户卸载数据至边缘服务器时,因其广播的特点,会被恶意窃听从而产生信息的泄漏,而在物理层进行处理往往被证实是一种有效避免泄漏的好方法,因此本文从物理层的约束出发对系统能效进行优化。

由于每个用户要处理的数据量不同,所以不可避免地出现时间上的差异,规定系统的用户协作方式如图2所示。设处理计算任务时间较长的用户的截止时延为T,根据用户处理计算任务的时间不同设置截止时延的分配比例α(0≤α≤1)。假设用户st处理的时间要大于用户w,将总的处理时间分为两个时隙,第1个时隙的时长为αT,第2个时隙的时长为(1-α)T,这样设置的目的是为了使得用户能够根据自身需要计算卸载的数据量灵活调整时隙的宽度。

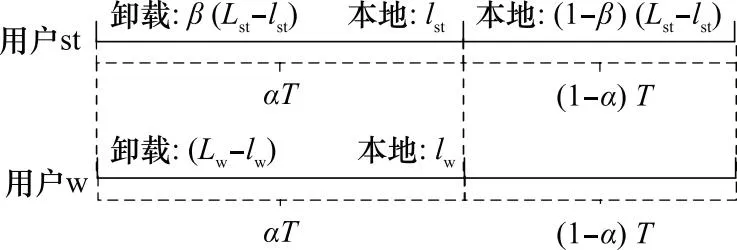
图2 NOMA用户对在卸载过程中的协作机制Fig.2 Cooperation mechanism between NOMA user pairs in the offloading process

MSHC方案的工作流程图如图3所示,可以看出,所提MSHC方案的工作流程分为3部分。首先需要根据用户的信道状态以及需求完成用户配对工作,将两个合适条件的强弱用户通过用户配对的选择算法[24]来匹配在一起;在第1个时隙中用户st与用户w同时进行卸载,此时可以依靠两个用户发射的混合卸载功率来干扰窃听者以保证信息安全,同时本地中央处理器(central processing unit, CPU)进行本地计算;在第2个时隙,出于公平性的考虑,已经完成卸载的用户w不再需要额外花费功率对用户st卸载过程中的安全性进行保障,处理计算任务量较多的用户只需将第一个时隙未完成卸载的剩余数据量转为本地计算即可,最后数据处理完成返回计算结果。

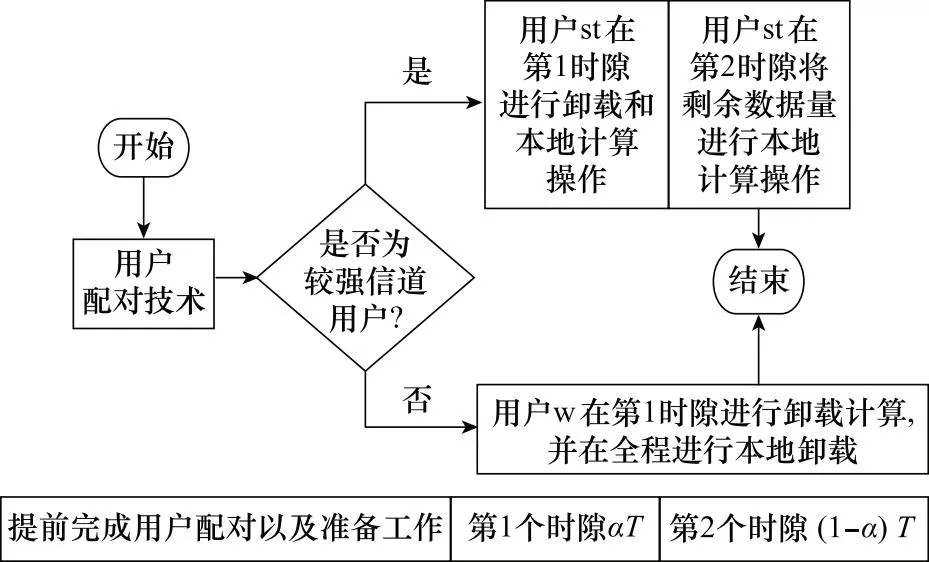
图3 MSHC工作流程图Fig.3 Work flowchart of MSHC

此外,两个用户在第1个时隙协作卸载时为了信息保密会产生额外的能耗,当卸载计算和保密的能耗总和大于本地计算的能耗时,显然绝对安全的本地计算是一个更好的选择,因此可将第2时隙用于原本需要卸载计算的数据量转为本地计算。这样通过改变st用户第2时隙的策略,达到兼顾公平性与安全性的目的。

设β(0≤β≤1)为第1个时隙的任务分配系数,可以依据能耗的指标动态调整用户卸载和本地计算的数据量,以此来实现能耗最小化的目的。用户st要处理的总数据量为Lst,第1个时隙卸载的数据量为β(Lst-lst),本地计算的数据量为lst,则剩余数据量(1-β)(Lst-lst)将在第2个时隙进行本地计算;用户w要处理的数据为Lw,在截止时延T内本地计算的数据量为lw,卸载只在第1个时隙进行,卸载的数据量为Lw-lw。因此,用户st的卸载速率(bits/s/Hz)为Rs,st=β(Lst-lst)/αBT,w用户的卸载速率为Rs,w=(Lw-lw)/αBT,其中B为信道带宽。

讨论用户st的卸载数据量大于等于用户w的情况,即在第1个时隙结束后,用户w完成卸载而用户st仍有剩余数据量没有卸载完成,数据量相反情况讨论类似。

1.1 基于NOMA-MEC的部分卸载

对于两个用户来说,在第1时隙均采用部分卸载策略,两个用户可以在相同的时间和频率资源上同时卸载其任务,此时基站b和窃听者e接收到的信号分别为

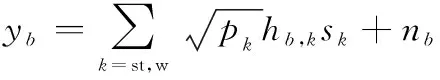
(1)

(2)

式中:sk∈C是用户k卸载时的任务承载信号,且E[|sk|2]=1;pk是用户的发射功率;nb和ne是零均值加性高斯白噪声(additive white Gaussian noise, AWGN)。

由于此前假设的|hb,st|2>|hb,w|2,基站会对收到的消息进行串行SIC解码,因此会先解码st用户的信息,此时w用户的信息会视为干扰,成功解码st用户信息后即可对w用户的信息户进行解码。因此基站接收到的用户st和w的解码信息的信号与干扰加噪声比(signal to interference plus noise ratio, SINR)分别为

(3)

(4)

窃听者接收到的解码信息的SINR分别为

(5)

(6)

需要注意,此处在构建SINR公式时,可以基于最坏情况假设的思想,假设窃听者在解码用户信息之前可以消除上行用户的干扰,使得窃听者信道SINR增加,更容易窃听,情况最坏,得到的结果保证在更加安全的情况下进行能耗优化,化简后的窃听者接收信号的SINR为

(7)

(8)

从合法接收方的角度来看,由于其既不知道窃听者的能力,也不知道瞬间的信道状态信息(channel state information, CSI),所以这种假设是为了确保任务的安全而进行的最坏情况[25]。在此假设下,可以得到由于对窃听容量不利的情况下可达到的系统保密率的下界。

此时,NOMA-MEC系统的部分卸载能耗可以表示为

(9)

1.2 基于NOMA-MEC的本地计算

设计算lk比特的数据所需的CPU周期为cklk,ck为本地计算每比特计算所需的CPU周期数,此时用户k进行本地计算消耗的能量可表示为CPU频率的函数,使得能耗最小的情况便是每个周期内CPU频率都是相同的,即fk=cklk/T[26]。

根据文献[27]中的结论,用户本地计算所消耗的能量与电容系数、处理1 bit数据所需的CPU周期数、本地计算任务量以及截止时延T有关,即

(10)

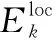
(11)

式中:ξk为电容系数;ck为计算1 bit任务所需的CPU周期数;lk为第一个时隙本地计算任务量且k∈{st,w}。

系统的总能耗为卸载能耗式(9)与本地计算能耗式(11)之和:

(12)

1.3 保密中断概率

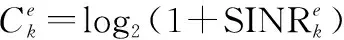
(13)

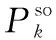
(14)

2 能耗最优化求解

在上述设置下,综合考虑系统中两个用户的通信安全可以将问题表示为最小能耗问题:

(15)

由于在文献[26]中已证得能耗最小的情况便是每个周期内CPU频率都是相同的即fk=cklk/T,因此可以取代式(15g)并给出化简后的优化函数表达式:

(16)

s.t. (15a)～(15f)

式(15a)、式(15d)和式(15e)分别对系统用户的本地计算任务量、发射功率以及时隙和任务分配比例做了限制;式(15b)和式(15c)表示的是用户卸载数据时的卸载速率,等于数据量与时间的比值;式(15f)则代表了保密中断概率的限制,使得系统能够在安全的条件下卸载数据。此时的目标函数和约束中的变量均为耦合形式,是非凸函数,难以直接求出最优值。因此,可以通过块坐标下降(block coordinate descent, BCD)算法循环迭代至收敛进行求解。先将α与β固定视为常数,通过调整lk和pk找到本次迭代的最小值后分别对α与β进行一维搜索,如此循环迭代直至收敛。将α与β的值固定视为常数得到的优化函数为

(17)

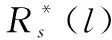
(18)

(19)

(20)

(21)

最后,将lst和lw进行遍历二维搜索,可以得到在固定α与β时的最优能耗值。

根据前文所述,固定l,p,遍历0≤β≤1求解最优能耗,则目标函数可以写为

(22)

利用式(13)对式(22b)进行推导可得

(23)

将式(23)与式(22a)合并后得到最终关于β的约束:

(24)

所以,在得到l,p的值以后,优化问题可以转换为固定α,l,p时求解关于β变量的能耗优化函数:

(25)

s.t. (24)

当α,l,p的值固定时,(1-β)3在[0,1]上进行最优搜索可以直接进行求解。

最后,将前两个子问题得到最优值时的变量β,l,p固定,从而对变量α的优化问题进行求解得到:

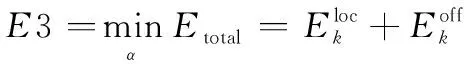
(26)

将式(26b)根据式(13)展开后可以分别得到st用户和w用户的截止时延分配比例α需要满足:

α≥c1

(27)

α≥c2

(28)

式中:

(29)

(30)

由于在系统中两个用户需要同时满足约束,故取两个约束的交集并与式(26a)结合可以得到化简后的优化问题与约束:

(31)

s.t. max{c1,c2}≤α≤1

(31a)

同理,对变量α进行遍历后可以得到固定β,l,p情况下的最优值。至此第一轮迭代已完成,将本轮搜索到的最优变量代入下一轮循环继续迭代直至收敛。根据以上的分析和结论,提出了基于BCD的能耗优化算法如算法1所示。

算法 1 基于BCD的能耗优化算法1: 设置 信道条件:hb,k,he,k,∀k∈{st,w} 分配比例:α,β2: 根据指定条件初始化lst,lw3: 根据式(18)～式(21)计算 pst,pw,Rs,st,Rs,w4: 第n次遍历式(17)后得到最优值E1(n)5: 初始化β6: 第n次遍历式(25)后得到最优值E2(n)7: 初始化α8: 第n次遍历式(31)后得到最优值E3(n)9: 重复步骤2～步骤8得到E1(n+1)、E2(n+1)、E3(n+1)10: 当|E3(n+1)-E3(n)|在设定精度ζ内时收敛11: 输出l*k,p*k,α*,β*,E*

BCD算法中,由于每个子问题在拆分后只与当前变量有关,其他变量均视为常数。显然,子问题函数为可微的凸函数,符合BCD求解函数全局最优的前提,当3个子问题的目标函数式(17)、式(22)、式(26)在每次迭代时均能得到最优解时,其数值在迭代过程中是单调非增的且优化变量有界[28]。综上所述,基于BCD的能耗优化算法收敛且可以通过子问题迭代优化得到最优值。

在以上分析的基础上,算法1在给常量赋值之后,将数据量lst,lw进行遍历循环计算,设输入用户st和用户w的数据量各为M和N,则MN为优化问题式(17)执行一次所代表的复杂度。优化问题式(25)与式(31)在每次确定了β的上限与α的下限之后可以直接进行凸函数的求解,在常量值已经确定且查找次数为L的情况下,复杂度均为1+log2L。至此一轮迭代已经结束,在此后的循环迭代过程中,每次结果都会利用上一次迭代结果的最优值进行计算,只要迭代的次数足够多,所得结果会无限接近于最优值并最终完成收敛,设迭代次数为K,则可以得到最终算法1复杂度为O[K(2+MN+2log2L)]

综合上述工作,在5G蜂窝网中,配对完成后的用户根据实时需要处理的计算量来动态调整两个时隙的长度以及卸载比例,以便于在每个时隙以最小化能耗为目标执行卸载策略。当用户间输入计算量差距较小时,可以延长第1个时隙持续时间,使其尽量在确保安全的情况下以更快速度和更低能耗完成卸载;当用户间输入计算量差距较大时,可以在第1个时隙适当增加功率尽量卸载一部分数据量,剩余计算数据量将以更安全的本地计算形式在第2个时隙完成计算。通过优化策略的动态调整和输入数据量的计算,最终将信息结果安全返回。

3 仿真结果分析

在本节中通过仿真软件对系统能耗进行性能分析和验证,并将提出的MSHC方案与其他基准方案的性能进行对比。考虑一个上行链路系统,并且依据参考文献[12]对常用参数常量进行设置,以此为根据进行仿真计算。在安全正交多址(orthogonal multiple access, OMA)-MEC方案中,用户在同一时间段只能存在一个用户进行卸载并且卸载速率要足够高以防止窃听,本地计算同步进行;在安全全卸载方案中,用户在数据处理的时间段同时进行数据的卸载,并不进行本地计算。

相关参数如表1所示,其中∀k∈{st,w},收敛精度ζ代表子问题结束循环迭代的条件。

表1 仿真参数Table 1 Simulation parameters

图4展示了用户输入的计算数据量与系统总能耗的关系,参考文献[16]提出的卸载方案设定了两个用户始终同时进行数据卸载的方案。由图4可知,本文提到的MSHC方案比起全卸载方案和OMA方案实现了更低的能耗水平,这是因为系统进行全卸载时,原来本地计算的数据也会进行卸载,此时系统会额外增加卸载功率从而保护用户的隐私。对于OMA-MEC方案,用户丧失了混合协作干扰的能力,因此需要额外增加卸载时的发射功率从而保证用户隐私。而文献[16]所提出的方案中,由于用户在每个时隙进行数据的卸载,会互相提供额外的干扰功率以保证用户的隐私不被窃听,由此带来的额外干扰功率增加了系统的总能耗。可以看出,在满足给定的保密中断概率的情况下,随着输入数据量的增加,系统处理数据的能耗也随之增加,同时类比于其他方案,MSHC卸载方案所降低的能耗也就越多,且在输入数据量达到4×105bits时,本文所提出的MSHC方案要比文献[16]中提出的方案降低30%能耗。

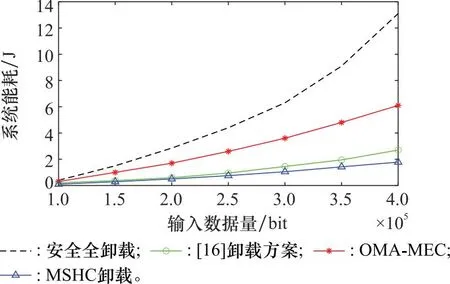
图4 用户输入数据量与系统总能耗Fig.4 Sum-energy consumption at users versus the number of computation input bits

图5展示了窃听者距用户的距离与系统的总能耗之间的关系,可以看出在保证保密中断概率的同时,所有方案都会随着窃听者距离的增加而能耗减小,这是因为窃听者距离用户越远,窃听者到用户的信道状态就会越差,干扰的增加使得窃听者更加难以辨别有效信息进行窃听。因此,维护信息安全所需的额外功率减少,使得最终系统能耗随窃听者距离的增加而降低。该图5中可以观察到,所提出的MSHC卸载方案相较于其他方案,能耗一直是最小的。并且窃听者距离越近,MSHC方案相较于文献[16]所提出的卸载方案降低的能耗就越多,随着距离的增加,二者之间的差值将基本不再变化。当窃听者距离用户超过110 m时,系统能耗将维持基本不变,此时可以看作系统中不存在窃听者,系统会实现完全保密的效果。

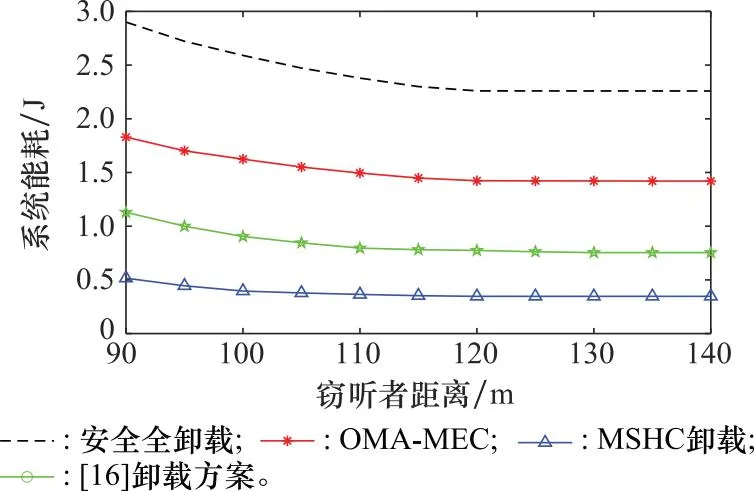
图5 窃听者距离与系统总能耗Fig.5 System sum-energy consumption versus the distance from the users to the eavesdropper

图6展示了用户保密中断概率与系统总能耗之间的关系,可以看出在输入数据量不变的同时,4种方案都会随着保密中断概率的增加而能耗降低。随着保密中断概率的提高,系统就越容易中断,对受到信息安全威胁时的容忍度越低,从而保证信息安全而额外消耗的能量就会越少。

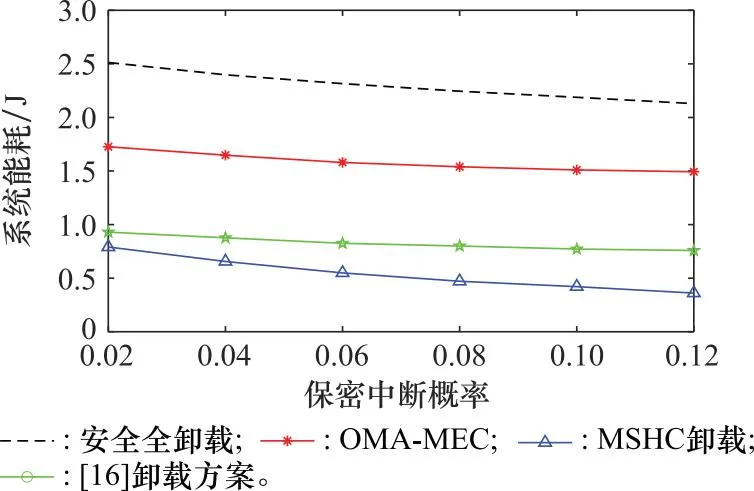
图6 保密中断概率与系统总能耗Fig.6 System sum-energy consumption versus the secrecy outage probability

此外,所有方案在保密中断概率较低时的能耗都是偏高的,因为每个方案都会为了更严格的保密而消耗更多的系统能量。且MSHC卸载方案在整个区间内相较于其他对比方案,其能耗都是最低的,随着保密中断概率的增加,MSHC方案降低能耗的速度更快。在保密中断概率为0.1时,本文所提及的安全MCHC卸载与OMA-MEC方案和文献[16]所提出的卸载方案进行对比,能耗分别下降了66%和40%。

图7展示了用户的总的执行时间与系统总能耗之间的关系,可以看出,随着截止时延的增加,能耗会逐渐减低并最终趋于稳定。这是因为截止时延较小时,对系统在短时间的计算处理速度和保密性能有较高的要求,因此能耗较高;而随着截止时延的增加,时间逐渐充裕,不需要消耗过高的能量在保密传输上,因此在输入数据量固定的情况下,后半段能耗会随着截止时延的增加逐渐趋于平稳。并且MSHC卸载方案在整个区间与其他方案相比都是最低的,即使在截止时延T=0.1 s时,MSHC卸载方案相较于全卸载和OMA-MEC方案的能耗都是最低的,这符合客观条件也印证了本方案相对于其他方案的优越性,为时隙资源缺乏和追求效率的低时延5G时代提供了借鉴。

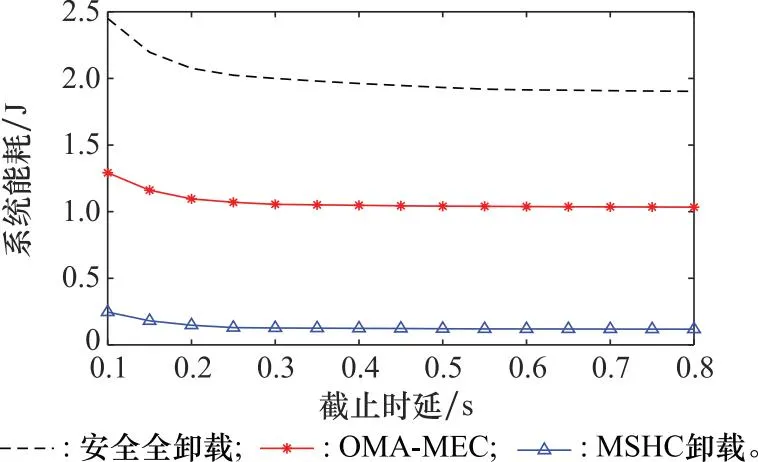
图7 时隙长度与系统总能耗Fig.7 System sum-energy consumption versus the time slot length

图8展示了不同变量参数下系统总能耗随输入的计算数据量的变化情况,并给出MSHC方案分别与3种不同参数卸载方案的对比结果。卸载方案①固定两个用户的本地计算数据量lst=1.8×105bits和lw=6×104bits;卸载方案②固定两个用户卸载时的发射功率pst=pw=300 mW;卸载方案③固定输入数据量较多的用户任务分配系数β=0.6。通过结果可以看出固定某些变量对系统能耗的影响。

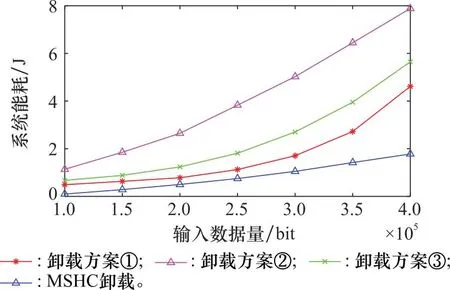
图8 固定不同卸载参数时系统总能耗随输入计算数据量变化图Fig.8 System sum-energy consumption versus the number of computation input bits by fixing the different offloading parameter

随着输入计算数据量的增加,系统的总能耗也会一直增加,卸载方案①设定了不同的用户本地计算数据量,可以看出虽然本地计算可以完全保证隐私安全,但并不能过度依赖本地计算,由于本地计算时的速度相比云服务器差距悬殊,短时间内的本地计算对计算机的性能提出了较高的要求,在有时延要求的前提下,本地计算数据量超出了合理的范围时,会额外调动更多资源与功率对数据进行处理,从而引起能耗的大幅增加;卸载方案②提升了卸载时用户的发射功率,可以看出,虽然较高的卸载功率可以降低时延和保护用户隐私,但功率过高会带来额外的能耗成本且卸载功率越高,系统的总能耗就会越大;卸载方案③则是固定了卸载计算数据量的分配比例β,在数据量较小时由于资源充足因此能耗差别并不大,而随着数据量的增加,一直维持这个分配比例不变则会导致本地计算的能耗增加,从而引起系统总能耗的增加,卸载计算的数据量需要根据输入计算的数据量而灵活调整。因此,图8很好地展示了MSHC方案在与多种参数设定方案结果对比的优越性。

4 结束语

本文研究了在恶意窃听者存在的情况下,保证卸载安全的两个用户在相同资源块上进行任务处理的能耗最优化。首先提出新的用户协作方式,并且根据已知条件对目标函数进行优化,通过BCD算法将复杂的目标函数分成3个容易处理的子问题,在保证保密中断概率的前提下采用BCD算法循环迭代得到用户的最佳卸载决策方案,实现了最小化能耗的目标。实验结果表明,与其他卸载方案相比,在截止时延合理的前提下,所提出的方案无论是能耗还是安全性能均优于其他方案,并为NOMA的发展与时隙的划分提供了新的思路。下一步将考虑计算密集型场景下,用户在不同时隙中依据时延和处理任务量等指标灵活选择计算卸载策略,研究平衡用户隐私安全与系统能耗的最优方案。