PCM信号间歇收发互补设计与回波重构方法

苏梦静, 刘晓斌, 吴其华, 艾小锋, 赵 锋, 肖顺平

(国防科技大学电子科学学院电子信息系统复杂电磁环境效应国家重点实验室, 湖南 长沙 410073)

sequence

0 引 言

在外场使用雷达信号进行试验时,存在难度大、成本高、周期长以及保密性差等问题[1-3],而室内场辐射式仿真则可以有效地规避这些问题,且相比于外场试验,室内场辐射式仿真具有灵活性好,可重复性高,逼真度高等优势。然而由于雷达信号脉冲时长对应的传播距离远大于暗室的尺寸,若直接将完整信号用于室内场辐射式仿真,会面临收发互耦的问题,以至于信号难以分离。而利用间歇收发思想[4],通过对信号发射和接收的间歇处理则可以有效地解决这一问题。

目前,利用间歇收发开展暗室仿真实验主要集中在线性调频(linear frequency modulation, LFM)信号。文献[5]利用间歇采样在时域上的间歇控制原理,将间歇采样理论与辐射式仿真技术相结合,提出了间歇收发处理方法,解决了辐射式仿真中脉冲雷达信号的收发互耦问题。文献[6]针对LFM雷达,结合压缩感知信号重构思想,提出一种抗间歇采样转发干扰的方法,准确地重构出目标一维高分辨距离像。文献[7]提出LFM信号经间歇收发后的高分辨距离像(high range resolution profile, HRRP)重构方法;与LFM信号相比,对相位编码的间歇收发处理与回波重构研究较少。脉冲编码调制(pulse code modulation, PCM)信号作为一种常用的脉冲压缩信号,具有较高的距离速度分辨率和较强的抗侦察、抗干扰能力,可以提高雷达系统的低截获能力,在现代雷达中得到了广泛的应用[8-9],但间歇收发会带来信号的损失,导致PCM信号距离像出现高旁瓣,因此研究PCM信号的回波重构很重要。

目前,针对LFM信号回波重构主要有两种方法:基于时频域滤波法[10]和基于压缩感知[11-16]的重构方法。时频域滤波法对LFM信号有效,但不适用于PCM信号。而基于压缩感知的重构方法则是将间歇收发的过程视为对雷达回波的随机观测,根据不同的雷达信号选择不同的稀疏变换域,最后选择贪婪迭代算法[17-23]、凸优化算法[24-26]、基于贝叶斯框架[27-29]等合适的算法从观测值中求解PCM信号,该方法有效地重构了PCM信号,但是计算较为繁琐复杂,重构性能与收发参数有关。所以,需要寻找一种操作更为简单的方法对间歇收发处理后的PCM信号回波进行重构处理。为此,本文提出间歇收发序列互补设计方法,即先利用一系列互补的序列对信号进行间歇处理,再对间歇后的信号进行重组拼接,依此来解决PCM信号间歇收发回波缺失问题,从而得到精确的目标距离像。

本文首先构建了PCM信号间歇收发回波模型,分析了PCM信号匹配滤波输出特性;然后给出了间歇收发互补序列设计方法,并通过回波拼接,实现PCM回波的精确重构;最后给出了仿真结果,验证了该方法的有效性和可行性。

1 PCM信号间歇收发处理方法

1.1 间歇收发流程

间歇收发流程如图1所示。PCM脉冲信号发射一段时间后,提前切换射频开关调至接收通道,开始接收目标回波信号,接收完成后,再次切换通道,切换至发射通道,继续发射信号,交替发射信号直至信号发射完毕。

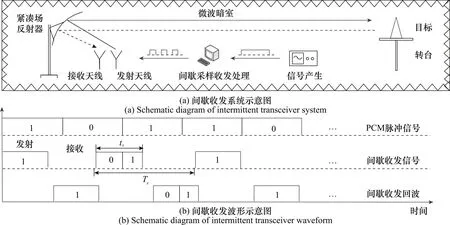
图1 间歇收发仿真场景Fig.1 Intermittent transceiver simulation scene

根据图1,通过间歇收发处理,雷达脉冲被截断为一系列子脉冲串进行发射,经过目标响应后回波信号仍为一系列子脉冲串。在实际系统中,通过精准的时延和波形控制能够保证发射信号的相位一致性和幅度连续性。

理想的信号表达式为单位幅度的矩形包络脉冲串信号,其时域波形如图1所示,可以写成

(1)

式中:rect(·)表示矩形脉冲;δ(t)表示冲激函数;n是脉冲数;τs为脉宽;Ts表示脉冲重复周期;*表示卷积运算。对PCM信号进行间歇收发等效于用雷达信号与p(t)做乘积。

假设雷达与目标之间的距离为R,目标尺寸为L,c为电磁波传播速度,子脉冲的宽度τs要小于回波往返时间,并且Ts不可以过大,不然会导致间歇采样收发之后PCM信号的部分码元无法被发射和接收,影响目标的测量性能,则PCM信号的间歇收发参数需要满足如下条件:

(2)

1.2 PCM信号脉压特性

设PCM信号为s(t),其时域可以表示为

(3)

(5)

(6)

对式(6)进行傅里叶变换得到信号频谱:

(7)

对其进行匹配滤波,得到脉压输出的频谱为

(8)

式中:

(9)

2 基于互补序列的PCM信号重构方法

2.1 构造互补序列

构造互补序列对PCM信号进行重构的思想为:通过设计一系列互补的收发控制序列,对相位编码信号分别进行间歇收发处理,再将间歇收发处理后的目标回波相加,实现对PCM信号回波在微波暗室中的精确重构。

基于原本的间歇收发流程,可以设置K组互补序列的间歇收发控制信号为pk(t),每组信号依旧为包络是矩形的脉冲串,每组信号间歇周期相同为Ts,脉冲宽度为τsk,要求K组的间歇收发控制信号满足包络彼此相邻且脉冲宽度相加为完整的间歇周期,示意图如图2所示。

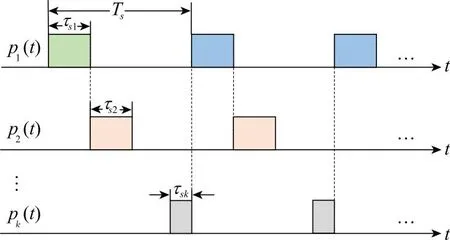
图2 K组互补序列间歇收发控制信号波形示意图Fig.2 K groups of complementary sequence intermittent transceiver control signal waveform diagram

则有以下关系:

(10)

对于K(K≥2,K∈N)组不同的间歇收发控制信号表达式则为

(11)

其频域形式为

(12)

式中:fs=1/Ts。

若要实现在一个发射周期内所有的信号全部可以接收,则子脉冲持续时间应满足τsk≤Ts/2。为了简化回波重构,可以设置前K-1组脉冲宽度都为τ1=τs1,则第K组脉冲宽度为

τ2=Tsmod(τs1)

(13)

式中:mod(·)为取余符号。则K组不同子脉冲宽度的间歇收发控制信号转换为子脉冲宽度为τ1和τ2的两组间歇收发控制信号。

2.2 PCM信号的回波重构与信息重构

在微波暗室环境中,回波的目标调制过程相当于将信号与冲激函数hT(t)=Aδ(t-Δt)进行卷积,其中A为目标对回波的幅度调制,Δt=2R/C,则完整的PCM信号回波y′(t)为

y′(t)=s(t)*hT(t)=

(14)

PCM信号经过k组间歇收发控制信号处理后,则为

(15)

那么,间歇收发处理后的回波xk(t)为

(16)

式中:N为脉冲Tp时长内间歇收发次数。

在实际间歇收发过程中,间歇收发周期Ts与脉冲宽度τsk不一定刚好是码元宽度τ的整数倍,导致经过间歇收发处理后的PCM信号进行匹配滤波处理后解析表达式难以获得。

对于PCM信号来说,模糊函数呈图钉形状,设PCM信号的频谱为S(f),则PCM信号的模糊函数为

(17)

式中:τ′和ξ分别为时延与多普勒频移。

间歇收发后,PCM信号的频域表达式为

S′(f)=S(f)*Pk(f)

(18)

Pk(f)为pk(t)的频域形式,则间歇收发后PCM的模糊函数为

χ(τ′,ξ+nfs)

(19)

在间歇收发中,一般取n=0阶作为目标的实际处,从而

χsk(τ′,ξ)=τskfsχ(τ′,ξ)

(20)

当τ′=0且ξ=0时为PCM信号的匹配滤波输出,由式(20)可知,经过第k个互补序列信号处理后的PCM信号目标处峰值幅度为完整信号的τskfs,仅存在幅度的差异,当ξ=0时,间歇收发后PCM信号模糊函数零点宽度与完整PCM信号回波相同。

根据式(10),则经过K组互补序列信号处理后的PCM信号相加之后得到的模糊函数在n=0处峰值幅度与完整信号峰值幅度相同,即

(21)

故设PCM重构回波为y(t),则重构回波为K组xk(t)相加的结果,即

(22)

从而实现PCM信号的回波重构。综上,结合图1和图2,具体的重构流程如图3所示。

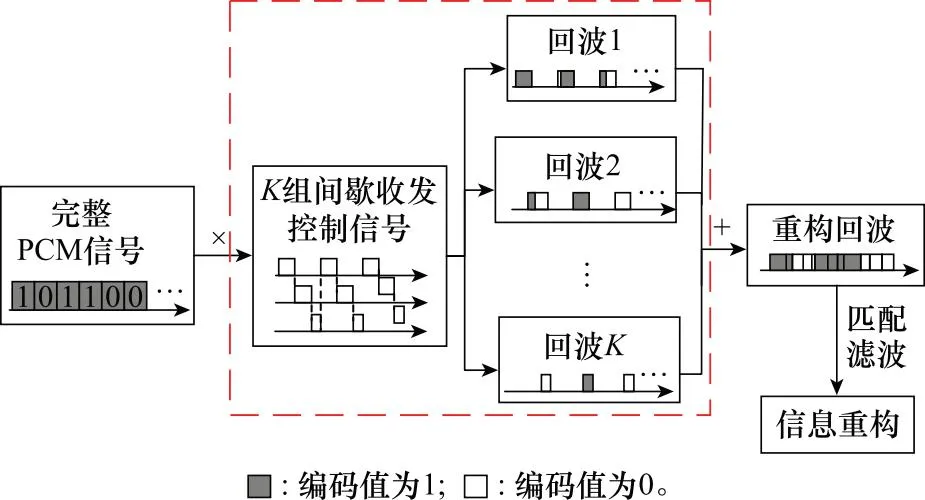
图3 PCM信号回波重构流程图Fig.3 PCM signal echo reconstruction flow chart

实现PCM信号重构的核心步骤如下。

步骤 1根据间歇收发参数设计互补序列间歇收发控制信号,同时与完整的PCM信号相乘,获得K组回波信号。

步骤 2将K组回波信号相加便可得到完整的重构回波。

3 仿 真

本文设计了一组互补序列解决间歇收发后的PCM信号在微波暗室中的回波重构,为验证其正确性,设置单个散射点目标进行计算机仿真验证,实验参数如表1所示。采用此参数进行PCM信号的间歇收发与回波重构,对其进行分析。

表1 实验参数列表Table 1 List of experimental parameters

间歇收发控制信号分别经过τsk=0.1 μs的时延,K=3时经过间歇收发控制信号处理后的PCM信号回波如图4所示。PCM信号回波的目标经过脉冲压缩后得到距离像,如图5所示,由于间歇收发周期大于码元宽度,部分码元未发射,导致间歇收发后得到的距离像旁瓣会高于完整回波得到的旁瓣。

图4 K=3时不同回波信号xskFig.4 Different echo signals xsk at K=3

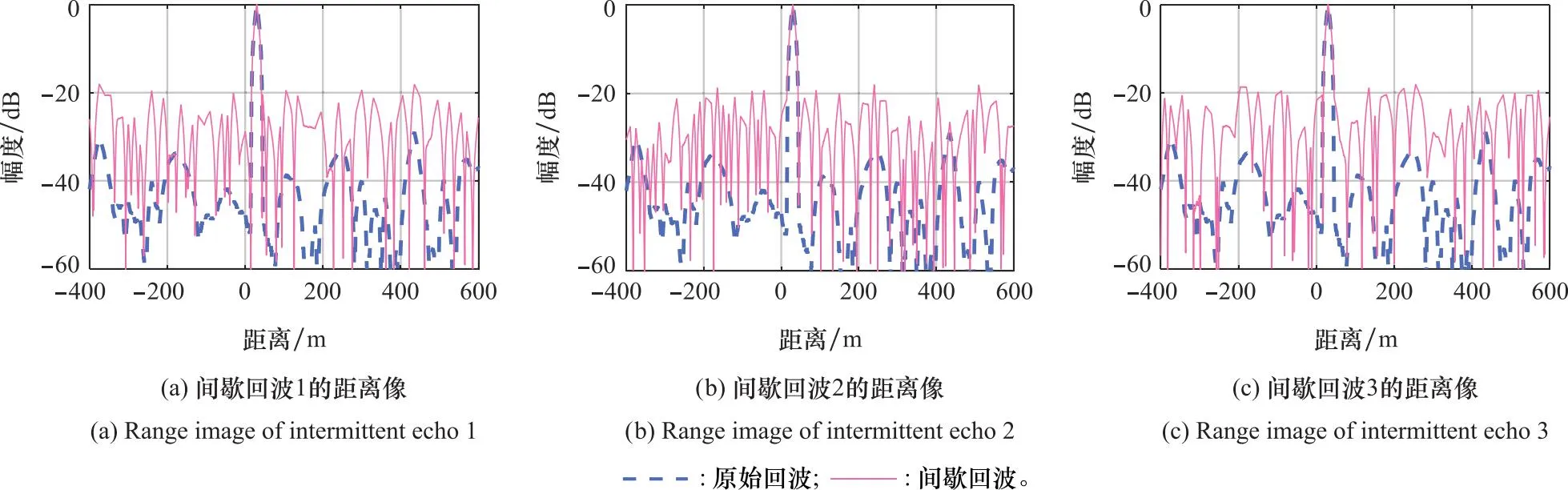
图5 间歇回波经过匹配滤波后与原始回波的对比Fig.5 Comparison between intermittent echo and original echo after matched filtering

图6(a)为间歇重构回波与原始回波的时域的对比,图6(b)为归一化脉压输出对比,重构回波匹配滤波输出结果与实际目标两侧的旁瓣与完整脉冲基本一致。

图6 间歇回波重构结果Fig.6 Results of intermittent echo reconstruction

针对多目标情况下,验证该方法对PCM信号回波重构的有效性,设目标径向距离上的3个散射点与天线距离为[15 m,25 m,30 m],对应的雷达散射截面(radar cross section,RCS)为[0.8,1.2,3.5],其参数与单个散射点目标一致,可得仿真结果如图7所示。

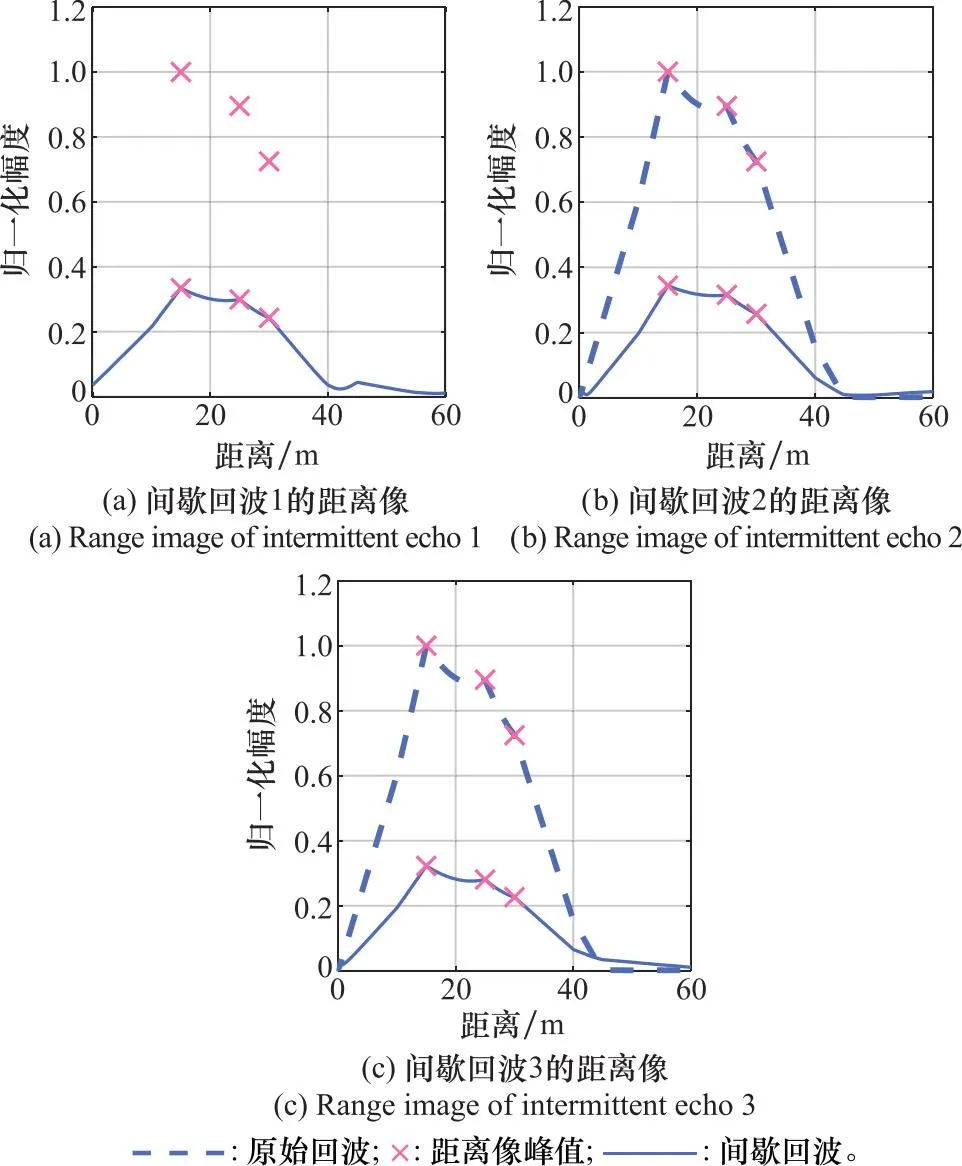
图7 距离像对比Fig.7 Range images comparison

从图7可以看出,3组不同的互补序列得到的脉压输出距离像中主瓣位置与完整脉冲相同,且峰值幅度大约为完整信号的τskfs。将3组经过互补序列间歇收发处理后的PCM信号相加之后可得到重构距离像,如图8所示,重构回波脉压距离像中主瓣位置和幅度与完整脉冲基本吻合,从而验证了采用互补序列对获取多目标高分辨一维像的有效性。为定量描述和比较重构的回波信号与完整回波之间的关系,更好的评估回波重构效果,可以用互相关系数来体现该方法重构回波的性能[30],即

(23)

式中:yr(t),y(t)分别表示重构回波信号和完整回波信号;Cov(·)表示互相关运算;Var(·)表示方差运算。互相关系数越接近1,回波重构效果越好。

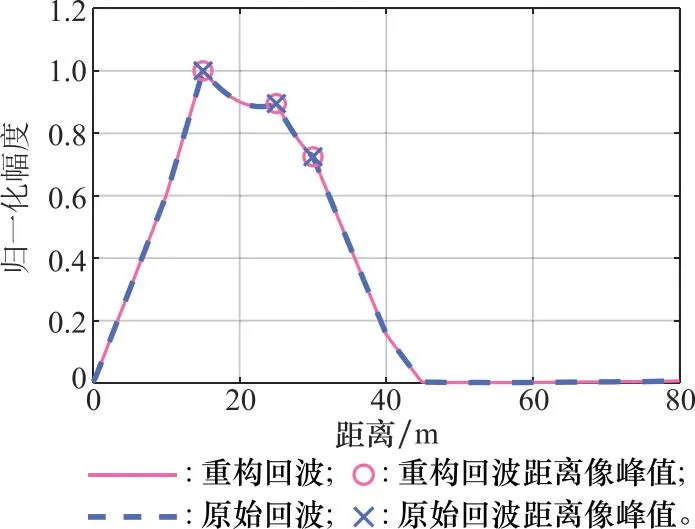
图8 重构距离像Fig.8 Reconstructing range image

根据间歇收发互补序列设计及回波重组方法,下面分析回波重构效果与接收机信噪比、间歇收发周期以及互补序列组数之间的关系,通过蒙特卡罗仿真实验,图9为仿真结果,互相关系数随着信噪比的增大而显著增大,当信噪比达到20 dB时,互相关系数达到90%以上,当信噪比为30 dB时,互相关系数接近1。对比不同曲线,在信噪比一定的情况下,间歇收发周期Ts越大,互补序列组数越大,互相关系数越小,由于低间歇收发周期与较小的组数对PCM信号的采样更加均匀,导致距离峰旁瓣幅度相对下降,改善了回波重构的性能。

图9 重构互相关系数Fig.9 Reconstruction of cross-correlation coefficient

将该方法与基于匹配滤波变换基的压缩感知重构方法[31]进行对比,设置码元个数为127,其余实验参数设置如表1所示。对比两者互相关系数,仿真结果如图10所示,可以发现在信噪比低的情况下,噪声对于基于压缩感知重构方法影响较大,而基于互补序列的方法互相关系数更高,重构效果更好;当信噪比达到10 dB后,两者重构互相关系数相似,均可达到95%以上。因此,本文提出的互补序列方法在对PCM信号回波进行重构中表现良好。

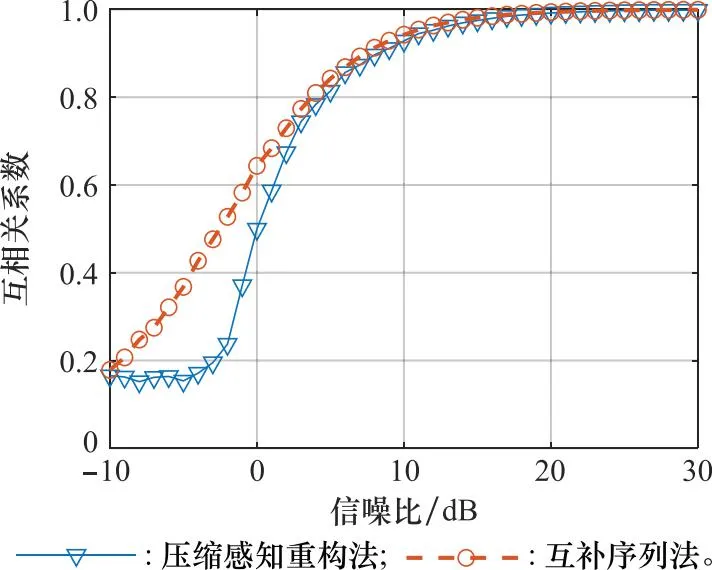
图10 不同重构方法互相关系数对比Fig.10 Cross-correlation coefficient comparison of different reconstruction methods

4 结 论

针对辐射式仿真中PCM信号间歇收发后回波重构问题,本文提出了基于互补序列回波设计方法。首先分析了PCM信号脉压之后的特点,接着给出了在微波暗室中重构PCM信号的具体方法,即用一组互补序列分别对PCM信号进行间歇处理,并对PCM信号回波进行重组拼接,实现对回波的精确重构。最后,实验仿真表明,该方法在单个散射点和多个散射点的情况下都具有良好的回波重构性能,所得到的重构回波与完整回波图像基本一致,并且在不同的间歇收发参数条件下,信噪比越高,间歇收发周期越大,互补序列组数越大,互相关系数越大,回波重构性能越好。与基于压缩感知的方法进行对比,该方法在低信噪比条件下互相关系数更高,回波重构效果更好。本文的方法对于PCM信号在暗室仿真中具有借鉴意义。