基于改进离散模拟退火遗传算法的雷达网协同干扰资源分配模型

尧泽昆, 王 超, 施庆展, 张少卿, 袁乃昌

(1. 国防科技大学电子科学学院, 湖南 长沙 410073;2. 国防科技大学电子信息系统复杂电磁环境效应国家重点实验室, 湖南 长沙 410073;3. 中国航空工业集团公司沈阳飞机设计研究所, 辽宁 沈阳 110035)

0 引 言

在信息化战场复杂的电磁环境中,雷达对目标的检测、识别、定位和跟踪对于战场情报的侦察获取有重要作用。雷达组网技术将多种体制,不同频段的雷达链接起来,形成了全方位、立体化、宽频带的探测体系[1],对突防导弹和战斗机的生存造成重大威胁。将干扰机进行组网协同是应对雷达网的措施之一,协同干扰机基于网内雷达的工作参数,判定雷达的威胁程度,结合现有的干扰资源,制定干扰分配方案,对干扰资源进行合理优化分配[2]。

协同干扰资源分配模型主要由干扰评估函数和函数最优解这两部分组成。文献[3]采用威胁等级作为干扰功率分配的依据,按照威胁等级的高低依次为目标分配干扰资源。文献[4-5]分别从时域、频域、空域、能量域以及对抗双方的工作体制、对抗样式等方面详细分析了雷达干扰效果影响因素,并结合各指标的隶属度函数完成干扰效果评估函数的构建,该方法现也被大多数研究者采用,但该方法构建干扰评估函数导致资源分配的效果过分依赖于隶属度函数各指标参数的设置,适用性较差。文献[6]以干扰机对雷达的压制概率公式为基础,构建雷达干扰资源分配目标函数,并用模拟退火(simulated annealin, SA)算法对目标函数寻优求解。文献[7]通过单雷达的测量误差,推导出组网雷达融合中心定位精度,并以此为目标函数,建立起组网雷达系统的干扰资源优化分配模型。文献[8-9]分别从干扰机的压制概率和雷达的检测概率出发,构建雷达干扰资源分配的目标函数,然而二者对不同恒虚警率(constant false alarm rate, CFAR)体制下雷达检测概率的变化差异没有深究。文献[10]通过将突防过程划分为搜索与定位两个阶段,分别以检测概率和定位精度作为各阶段的干扰评估指标,构建了自适应的干扰评估函数,并用粒子群算法对目标函数寻优,但是其检测概率模型对应于零均值白噪声的理想情况,运用在干扰的背景下效果不佳。

综上所述,本领域研究采用的算法大多是传统的群智能算法,运行效率较低。干扰评估函数的构建多是基于理想情况,缺乏适用性。针对以上这些问题,本文基于干扰信号脉压增益分析,推导出干扰作用下多种CFAR检测器雷达的检测概率,映射得到干扰后雷达网融合检测概率,并以此为干扰效果评估函数,建立干扰资源的分配模型。随后利用改进离散SA遗传算法(improved discrete SA genetic algorithm, IDSA-GA)对资源分配模型寻优求解,IDSA-GA在SA-遗传算法(genetic algorithm, GA)的基础上引入随机密钥,引入的随机密钥解决了子代可行性问题,显著减少了运算量,加快了算法的收敛速度;并在迭代的过程中增加记忆功能,克服了过早收敛的现象,提高了算法的搜索精度。仿真结果验证了算法的有效性。

1 干扰下不同CFAR体制雷达检测概率分析

本文以多机伴随分布式干扰为作战场景,战场环境模拟如图1所示。

图1 多机伴随分布式干扰Fig.1 Multi-aircraft adjoint distributed interference

本文考虑随机移频噪声、灵巧卷积噪声、间歇采样转发噪声这3种干扰样式,干扰信号由雷达发射信号经过调制得到,可以获得部分脉冲压缩增益,3种干扰信号脉冲压缩增益ej表达式如表1所示。

表1 干扰信号脉冲压缩增益Table 1 Pulse compression gain of interference signal

关于移频干扰与卷积噪声干扰信号的增益求解可参考文献[11-13]。对于间歇采样干扰信号,在采样占空比为0.5的情况下,本文将干扰信号脉压后的0阶与±1阶分量都纳入考虑范围[14],即可得到表1结果。基于干扰信号脉压增益ej,容易得到CFAR前信号的干噪比,回波信号信噪比的计算过程与干噪比类似,这里不再赘述。

本文将4种不同的CFAR检测器纳入研究范畴,其检测概率表达式Pd如表2所示。

表2 干扰下不同CFAR检测器的检测概率Table 2 Detection probability of different CFAR detectors under interference

表2中,Γ(x)为Gamma函数;S为回波信号的信噪比;I为干扰信号的干噪比;J是干扰信号占据的参考单元数;k为有序统计恒虚警率(ordered statistics constant false alarm rate, OS-CFAR)检测时选用的样本序号值;T为门限因子。

在均匀杂波噪声背景中,干扰情况下单元平均CFAR(cell averaging CFAR, CA-CFAR)和OS-CFAR的检测概率求解参考文献[15]。对于单元平均取小CFAR(smallest order CFAR, SO-CFAR)与单元平均取大CFAR(greatest order CFAR, GO-CFAR)体制的雷达,干扰情况下二者对应的检测概率表达式非常复杂,在干扰机主瓣干扰的情况下,干噪比I值很大,可近似看成无穷。在文献[16]中,Weiss给出了在I→∞时,二者检测概率Pd的表达式。

根据表2给出的检测概率计算公式,给定CFAR检测器种类和各项参数值,结合第2节中得到的信号信噪比和干噪比,可以得到单部雷达的检测概率Pd为

Pd=Pd(S,I,N,J,T,k)

(1)

2 干扰目标函数的构建

本文选用雷达网融合检测概率作为干扰目标函数对协同干扰效果进行评估。对干扰方而言,雷达网整体检测性能越低,证明干扰资源分配后达到的干扰效果越好。

分布式干扰机掩护目标遂行作战任务时,假设现有的干扰机集合为J={J1,J2,…,JN},可选择的干扰样式集合为Q={Q1,Q2,…,QL},需要干扰的雷达集合为R={R1,R2,…,RM}。干扰决策矩阵用Xnm表示,矩阵中的元素xnm=1表示第n部干扰机对第m部雷达进行干扰,若值为0,则表示未进行干扰。干扰样式矩阵用Ynl表示,矩阵内元素的表示原理与决策矩阵相同,干扰资源分配的模型如图2所示。

根据单部雷达的检测概率Pd,结合干扰资源分配模型,雷达网的检测概率矩阵可表示为E={P1,P2,…,PM},元素PM表示如下:

(2)

式中:Pmnl(xnm,ynl)表示第n部干扰机采用第l种干扰样式对第m部雷达进行干扰后的检测概率;PM为雷达网内第m部雷达在干扰环境下的检测概率矩阵,规模大小为M×N×L,矩阵中每个元素值可通过式(1)计算得到。

本文定义单次脉冲检测下,第m部雷达对目标的检测概率为Pdm,结合式(2),可以得到雷达m检测概率的表达式

(3)

组网雷达的融合检测概率是组网融控中心对目标的发现概率,雷达网采用不同的融合规则会导致融合检测概率有差别,具体的融合规则如表3所示。

表3 组网雷达融合规则Table 3 Netted radar fusion rules

组网系统内的雷达通过信息融合技术,将检测得到的目标点迹送往组网融控中心进行点迹的融合处理。当多部雷达同时对目标进行探测时,只要任意一位网内成员发现了目标,并将形成的点迹信息送往融控中心,都可以认为目标被雷达网检测发现。这种情况下组网雷达系统发现目标的融合概率为

(4)

后续的仿真验证以式(4)作为协同干扰资源分配模型待优化的目标函数。

3 IDSA-GA原理及流程

在第2节中,本文建立了干扰资源分配的0-1规划模型。在对干扰决策和样式矩阵进行编码的过程中,无论是采用二进制还是整数编码的形式,随着干扰机数目的增加,算法的搜索空间都会呈现几何倍的扩大。再者,干扰资源分配是在多约束条件下进行的离散组合优化问题,传统的GA一般用于连续函数的优化,如果将其运用在离散问题的优化上,算法得到的子代个体会出现超出约束边界的情况,这导致算法需要对每个子代的可行性进行求解,延缓了运行速度。

针对以上问题,本文提出一种引入随机密钥[17]的IDSA-GA。

Bean在文献[17]中提出了引入随机密钥解决算法离散化问题的方法。利用随机密钥对干扰决策矩阵和样式矩阵进行编码时采用实数码的形式,该实数编码由{1,2,…,l}的随机整数加上(0-1)的随机偏差两部分组成,如表4所示。

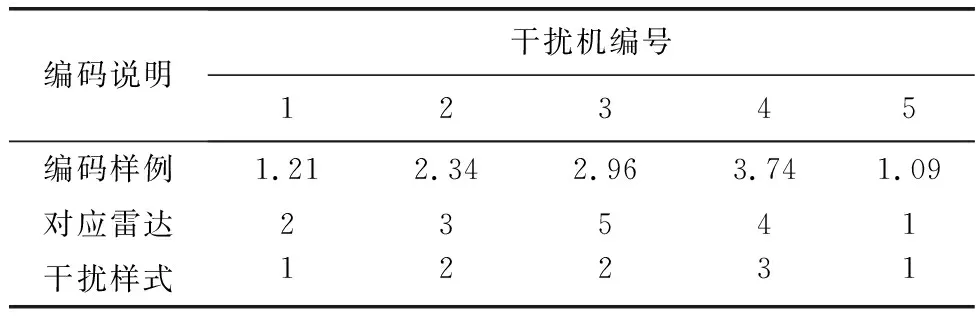
表4 随机密钥编码Table 4 Random key encoding example

表4中编码的顺序值代表干扰机的编号,编码的整数部分表示为干扰机选择的干扰样式,小数部分按照从小到大的排列顺序表示雷达的编号。对于编码1.21,顺序值和整数位值为1,小数位值排在第2位,表示干扰机1采用干扰样式1对雷达2进行干扰。引入随机密钥的实数编码形式简洁,有效解决了子代染色体基因可行性的问题,可以显著减少计算量。

文献[18]提出了一种SA-GA,本文在此基础上加以改进,在编码阶段引入随机密钥,并增加了记忆存储的功能,每次迭代时选取一部分高适应度个体,并将其存储起来,不进行交叉变异直接复制到下一代。

本文提出的IDSA-GA对干扰资源分配模型寻优流程如下。

步骤 1对种群进行初始化,随机产生50个引入随机密钥的实数编码序列表征干扰机对雷达的决策和干扰样式矩阵,这些实数编码构成了GA的初始种群。

步骤 2设置SA算法初温T_max,温度下限T_min,开始迭代时,温度T=T_max,设置交叉比例为p1,变异比例为p2。

步骤 3当T>T_min时,重复步骤4～步骤8。

步骤 4假设雷达网的融合检测概率为Pd,适应度函数值为1-Pd,将种群中的个体按适应度的高低进行排序,将适应度高的个体按一定比例直接复制到下一代,不进行交叉变异。

步骤 5从种群按照p1的比例选取n1对样本作为父代染色体。假设父代染色体为x1和x2,二者进行单点交叉后产生子代染色体y1和y2。如果y1的适应度大于x1,则用子代染色体y1替换掉种群中的父代x1。如果y1的适应度小于x1,则生成一随机数rand,当rand>exp{[f(y1)-f(x1)]/T},接受子代染色体y1,否则保留原来的父代染色体x1。

步骤 6按照p2的比例选取n2个染色体样本进行变异,父代染色体为x3,子代为y3,按照SA算法的规则对变异后的染色体进行选取,选择流程与步骤5相同。

步骤 7以公式T=αT对算法温度进行更新,本仿真取α为0.98,返回步骤3。

步骤 8当T≤T_min,满足终止条件,输出最优解。

4 仿真验证

本文仿真研究的作战场景为5部干扰机围绕着目标做伴随飞行,掩护其突防组网雷达系统。雷达网内有5部雷达,干扰机和掩护目标突防雷达网的轨迹如图3所示。图3中,实线代表掩护目标的航线,虚线代表干扰机的航线。选取航行某一时刻进行仿真,该时刻掩护目标与干扰机的位置坐标列如表5所示,雷达坐标和部分参数如表6所示。参考单元数数目N为16,OS-CFAR检测时选用的k值为6,干扰信号占据的单元数J为3。

图3 干扰机与掩护目标突防轨迹Fig.3 Penetration trajectory of jammers and the protected targets

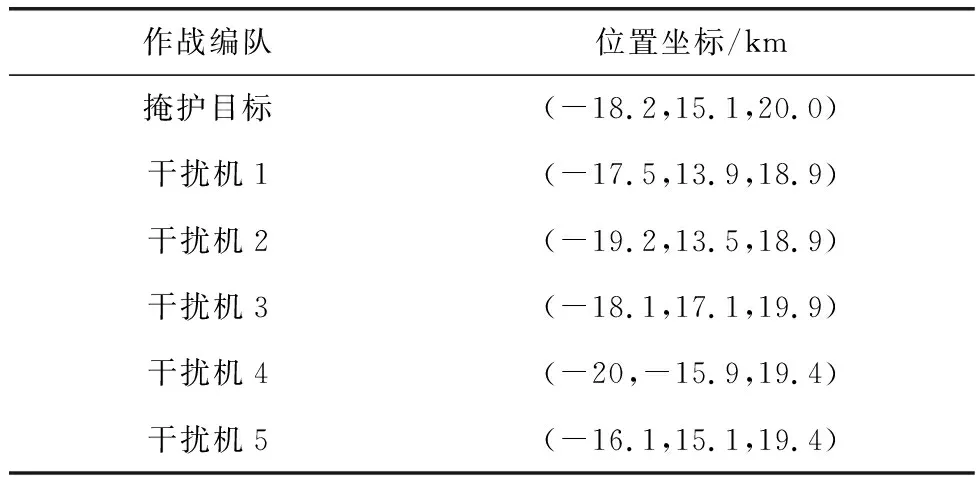
表5 掩护目标与干扰机的位置坐标Table 5 Location coordinates of protected targets and jammers

表6 雷达位置坐标,CFAR体制与接收机带宽Table 6 Position coordinates, CFAR systems and receiver bandwidth of radar

在进行干扰前,干扰机会对雷达信号进行侦查与分选,提取有用信息,并根据获取的先验信息制定合理的干扰资源分配方案。进行干扰时,干扰机可以采用随机移频干扰、灵巧噪声卷积、间歇采样重复转发干扰这3种干扰样式对雷达网进行协同干扰,雷达和干扰机及干扰信号的基本参数分别如表7和表8所示。

表7 雷达的仿真参数设置Table 7 Simulation parameter setting of radar

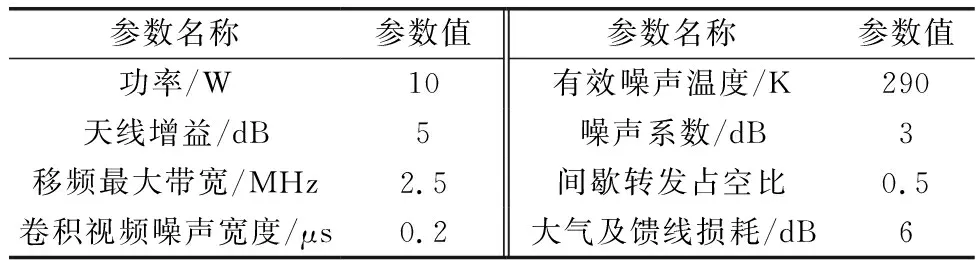
表8 干扰机工作及信号参数设置Table 8 Operation and signal parameters setting of jammer

使用本文提出的IDSA-GA对干扰资源分配模型进行求解,干扰资源的最优分配结果如表9所示。

表9 干扰资源最优分配结果Table 9 Optimal jamming resources allocation result

文献[19]提供了一种自适应的GA,加上文献[18]提出的SA-GA,使用这两种算法与本文提出的IDSA-GA算法共同对资源分配模型进行寻优求解。在下文对算法性能的分析中,雷达网融合检测概率作为干扰目标函数,函数值越小说明干扰效果越好。种群规模为50,进化代数为100,3种算法单次运行结果对比如图4所示。从图4中可知,相比于文献[18-19]算法,本文提出的IDSA-GA算法搜索能力更强,更易收敛到最优解。

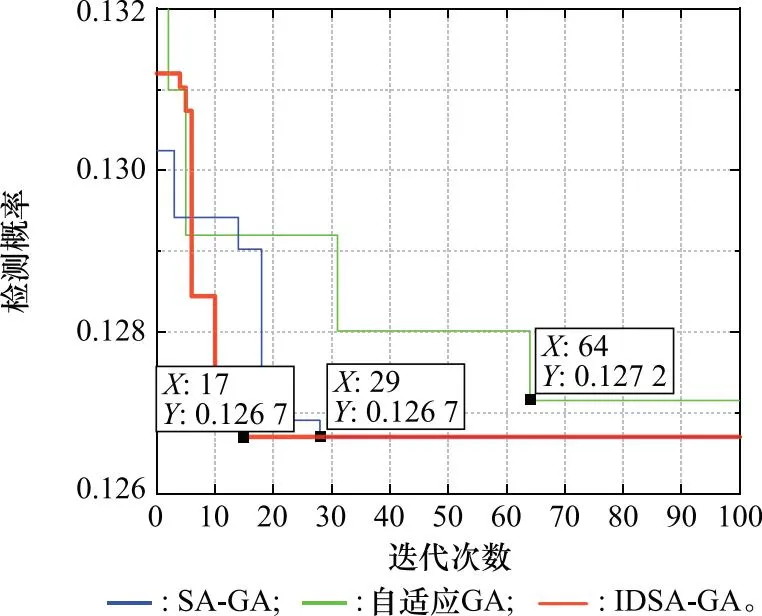
图4 单次运行结果对比图Fig.4 Comparison diagram of single run results

为了进一步对比3种算法的收敛稳定性和寻优能力,本文将每种算法各进行100次的蒙特卡罗仿真,记录每次运行的收敛代数,并对每次检测概率收敛值与全局最优解进行求差。算法各自独立运行100次后,收敛代数与收敛误差对比如图5所示,算法的总体性能对比如表10所示。

图5 算法性能对比Fig.5 Comparison of algorithm performance

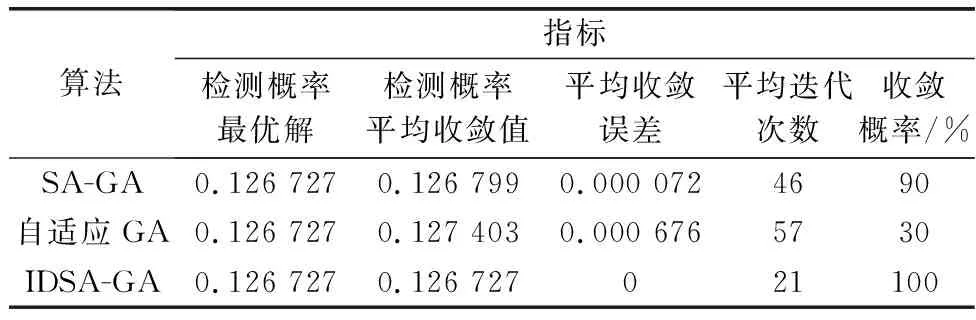
表10 算法总体性能对比Table 10 Overall performance comparison of algorithms

结合图5和表10来看,IDSA-GA相比于其他两种算法,达到收敛需要的迭代次数少,收敛的更快,收敛误差也更小。相比于其他两种算法,IDSA-GA有显著优势。

IDSA-GA算法优越性在于其编码时引入了随机密钥,大大减少了运算量;算法采用SA的方式接收交叉和变异的新个体,利用温度T对迭代次数进行控制。在进化初期T值很大,算法接收新解的概率很高,可以大大增强算法的搜索能力,解决过早收敛的问题。随着种群的进化,种群中最优个体不断增多,温度T以α的比例逐渐缩小,算法接收新解的概率下降,使得结果更易趋于收敛;算法还加入了记忆功能,将适应度高的种群个体有效的进行保留,增强了算法收敛到全局最优解的能力。

5 结束语

本文基于对几种典型干扰样式脉冲压缩增益和不同CFAR体制雷达检测概率的分析,创建了以融合检测概率为目标函数的干扰资源分配模型,提出一种引入随机密钥的IDSA-GA对干扰资源的最优分配进行求解,解决了子代可行性的问题,该算法收敛性好,寻优能力强,引入的随机密钥可以大大减少算法的运算量,有效加快了算法的运行速度。仿真验证了干扰资源分配模型与算法的有效性,为组网雷达的协同干扰提供了新思路。