计算Lyapunov指数的模糊C均值聚类小数据量法

高允报，孙玉泉

(北京航空航天大学数学科学学院，北京 100191)

Lyapunov指数(LE)可以判断动力系统的混沌状态，在研究混沌运动特性中起着非常重要的作用，是衡量动力学特性的一个重要定量指标，它表征了系统在相空间中相邻轨道间收敛或发散的平均指数率[1].系统的混沌状态可以通过LE的正负来判断，所以研究如何计算LE就非常必要.

近年来国内外学者对LE的计算方法做了很多研究.严雯等[2]利用定义法求解了Logistic模型的最大Lyapunov指数(LLE)；Wolf等[3]利用Wolf法计算出几种混沌系统的LLE；Rosenstein等[4]提出小数据量法来计算LLE.然而定义法只适用于计算已知系统的LE；Wolf法计算LLE时过程较为复杂且结果往往不精确；小数据量法在不知系统方程而仅可获得离散数据的情况下计算LLE时，对于线性区域的判断往往通过直观观察，导致结果误差较大.本文将模糊C均值聚类算法用于小数据量法线性区域的选择，提出了模糊C均值聚类小数据量法，提高了计算时间序列LLE的精度，且通过适当增加每次迭代的离散时间步长加快了计算LLE的速度.

1 预备知识

定义1.1Lyapunov指数：

(1)

经过n次迭代后，这两点的距离变为

δxn=|fn(x0+δx0)-fn(x0)|.

(2)

定义LE如下[5-6]：

(3)

对于一般的n维动力系统，定义LE如下：设一个n维动力系统xn+1=F(xn)(Rn→Rn)，将系统的初始条件取为一个无穷小的n维小球，半径取为ε(0)，由于演化过程中的自然变形，小球将变成椭球，见图1.将椭球上所有主轴按照其长度排列，那么第i个LE根据第i个主轴的长度εi(t)的增加速率[7-8]定义为

(4)

最大的λi称为LLE.系统的混沌状态可以通过LLE的正负来判断，当LLE大于零时系统处于混沌状态；当LLE小于零时系统稳定.

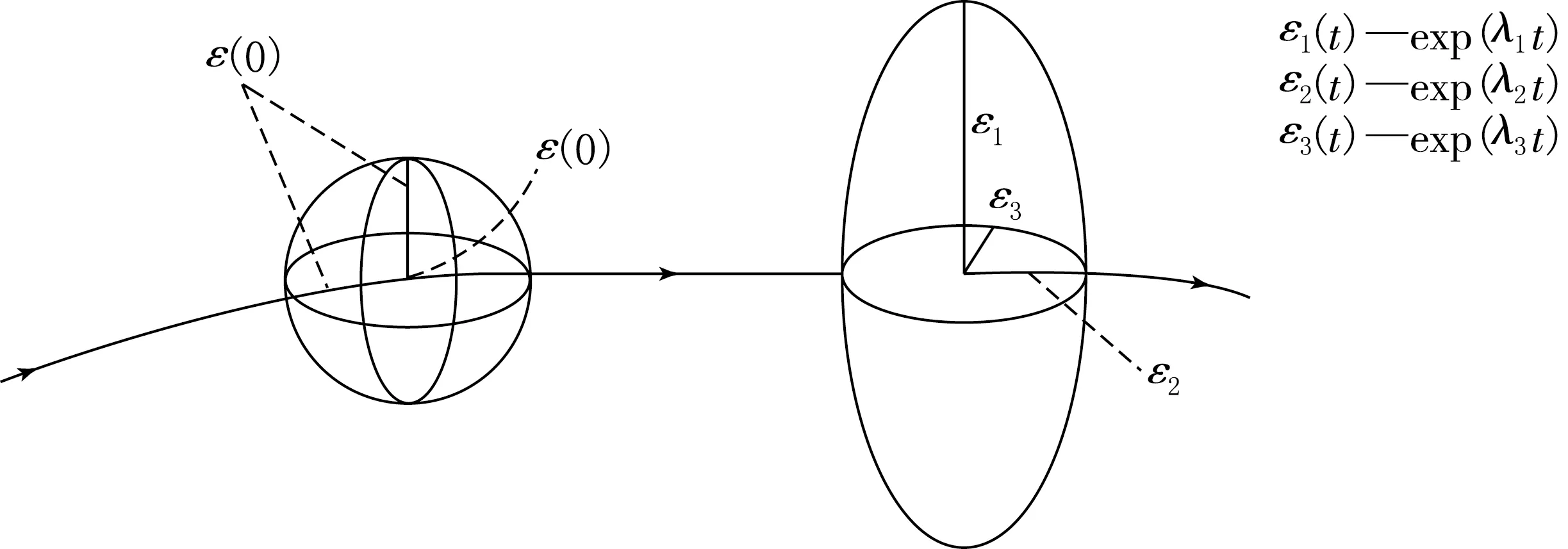
图1 3维球面随时间的演化

根据定义计算LE的方法称为定义法，由于定义法计算LE时只适用于给定的系统，不能求时间序列[7-9]的LLE，因此Rosenstein提出了小数据量法.

定义1.2小数据量法：

对于时间序列{x1，x2，…，xN}的LLE可以用小数据量法，对于时间序列通过计算得[10]：设嵌入维数m，时间延迟为τ，平均周期为P，则重构相空间为

Xi=[xi，xi+τ，…，xi+(m-1)τ]，i=1，2，…，M.

(5)

在重构的相空间中寻找每个参考点Xj的最近邻点Xj′，记

djj′(0)=min‖Xj-Xj′‖.

(6)

其中|j-j′|>P，P为时间序列的平均周期，可以通过基本轨道上每个点的平均发散速率计算.

对于每个参考点Xj，计算出其与最近邻点Xj′的第i个离散时间步长后的距离djj′(i)为

djj′(i)=min‖Xj+i-Xj′+i‖，i=1，2，…，min(M-j，M-j′).

(7)

假定参考点Xj与最近邻点Xj′的指数发散率为λ1，那么

djj′(i)=Cjeλ1(i·Δt)，Cj=djj′(0)，

(8)

上式两边取对数得

lndjj′(i)=lnCj+λ1(i·Δt).

(9)

由(9)式可以看出lndjj′(i)与变量i满足线性关系，其曲线斜率为λ1Δt.

因此固定i，对所有的lndjj′(i)求平均再除以Δt，得到平均发散程度指数

(10)

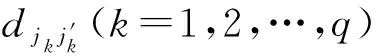
2 模糊C均值聚类小数据量法

2.1 模糊C均值聚类算法

在众多模糊聚类算法中，模糊C-均值算法通过优化目标函数得到每个样本点对所有类中心的隶属度，从而决定样本点的类属以达到自动对样本数据进行分类的目的.过程如下：

(11)

(12)

采用迭代的方法，通常情况下取初始隶属度矩阵为每行为随机单位向量的矩阵，b=2，最大迭代次数为100，隶属度最小变化量为10-6，求解(11)和(12)式，直至满足收敛条件，得到最优解.

2.2 模糊C均值聚类算法选择线性区域

在小数据量法计算LLE时将模糊C均值聚类算法用于选取线性区域，具体过程如下：

(1) 运用模糊C均值聚类算法将y(i)数据分为不饱和区域(y(i)达到基本稳定之前)和饱和区域(y(i)在一条水平直线附近做微小波动)两类，如图2所示.

(2) 对于不饱和区域需要选出线性区域，用二阶差分ddy(i)近似替代二阶导数，对于不饱和区域的二阶差分(i，ddy(i))将其分成3类，如图3所示.结合不饱和区域平均发散程度指数的图像与不饱和区域的二阶差分的图像可以看出，当i较小时离散程度较大，当i较大时线性化程度较低.因此将不饱和区域的y(i)-i分成3类，如图4所示，选取第2类作为最终选择的线性区域，其斜率就是LLE.

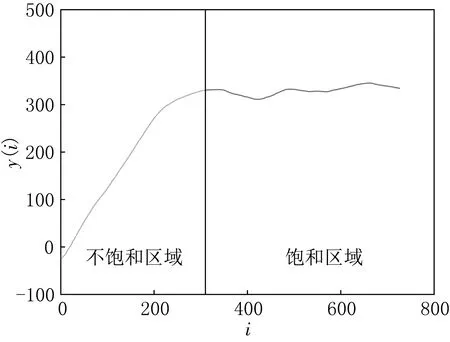
图2 平均发散程度指数

图3 不饱和区域平均发散程度指数二阶差分分类

2.3 模糊C均值聚类小数据量法

对于时间序列{y1，y2，…，yN}，嵌入维数my，时间延迟为τy，平均周期为Py，则重构相空间为

Yi=[yi，xi+τy，…，yi+(my-1)τy]，i=1，2，…，My.

(13)

在重构的相空间中寻找每个参考点Yj的最近邻点Yj′，有

Djj′(0)=min‖Yj-Yj′‖.

(14)

其中|j-j′|>Py，Py为时间序列的平均周期，可以通过基本轨道上每个点的平均发散速率计算.

对于每个参考点Yj，计算出其与最近邻点Yj′的第ni(n=1，2，3，…)个离散时间步长后的距离为

Djj′(ni)=‖Yj+ni-Yj′+ni‖，

(15)

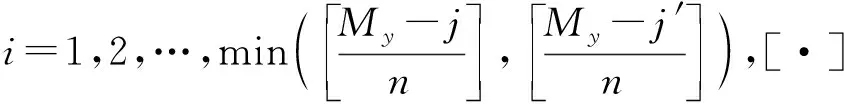
假定参考点Yj与最近邻点Yj′的指数发散率为λ，那么

Djj′(ni)=Ajeλ(ni·Δt)，Aj=Djj′(0)，

(16)

上式两边取对数得

lnDjj′(ni)=lnAj+λ(ni·Δt).

(17)

由(17)式可以看出lnDjj′(ni)与i满足线性关系，其曲线斜率为nλΔt.

因此固定i，对所有的lnDjj′(ni)求平均再除以Δt，得到平均发散程度指数

(18)

3 数值实验

为了验证模糊C均值聚类小数据量法的有效性，以典型的Lorenz系统[11]为例，选两组不同的系数进行数值实验.Lorenz系统为

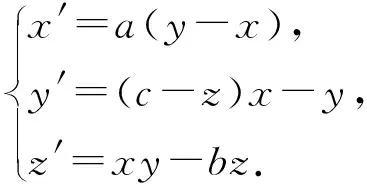
(19)

取4个不同的初始点A1=[0.046 2，0.097 1，0.823 5]，A2=[0.694 8，0.317 1，0.950 2]，A3=[1，4，10]，A4=[0.119 0，0.498 4，0.959 7]，取a=16，b=4，c=45.92，此时LLE理论值为1.501 5.取积分步长为0.01，演化点3 000个，用小数据量法和模糊C均值聚类小数据量法(重构维数为5，时间延迟为10，平均周期为40)计算LLE所得结果与误差率见表1，小数据量法简称AL1，模糊C均值小数据量法简称AL2.

取4个不同的初始点A1=[0.046 2，0.097 1，0.823 5]，A2=[0.694 8，0.317 1，0.950 2]，A3=[1，4，10]，A4=[0.119 0，0.498 4，0.959 7]，取a=16，b=4，c=45.92，此时LLE理论值为1.501 5.取积分步长为0.01，演化点5 000个，用小数据量法和模糊C均值聚类小数据量法(重构维数为5，时间延迟为10，平均周期为40)计算LLE所得结果与误差率见表2.

取初始点A1=[0.046 2，0.097 1，0.823 5]，取a=16，b=4，c=45.92，此时LLE理论值为1.501 5.取积分步长为0.01，分别演化3 000个点与5 000个点，用模糊C均值聚类小数据量法(重构维数为5，时间延迟为10，平均周期为40)每次分别演化i，2i，3i，4i(i的取值见上文)个离散时间步长，LLE计算结果与运行时间见表3.

取初始点A1=[0.046 2，0.097 1，0.823 5]，取a=10，b=8/3，c=28，此时LLE理论值为0.881 0.取积分步长为0.01，分别演化3 000个点与5 000个点，用模糊C均值聚类小数据量法(重构维数为5，时间延迟为25，平均周期为40)每次分别演化i，2i，3i，4i(i的取值见上文)个离散时间步长，LLE计算结果与运行时间见表4.

从表1与表2结果可以看出，对比于小数据量法，文中提出的模糊C均值小数据量法计算LLE可以提高计算精度；从表3与表4结果可以看出，模糊C均值小数据量法计算LLE时随着每次迭代的离散时间步长的增加，计算时间将缩短，但每次迭代的离散时间步长不宜过大.实验结果验证了算法是有效可行的.

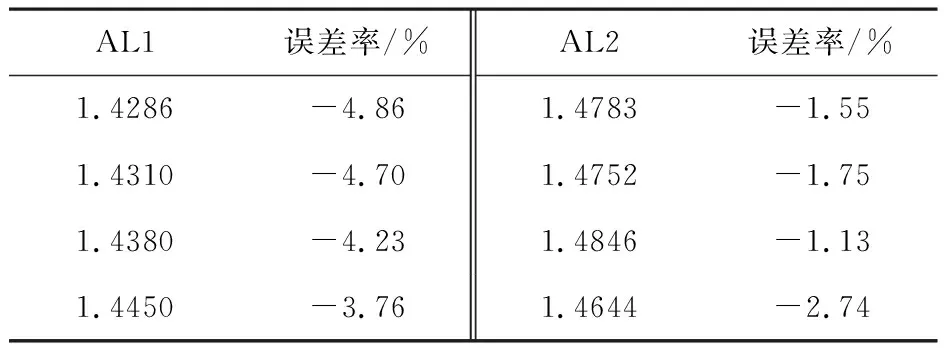
表1 3 000个演化点时小数据量法与模糊C均值小数据量算法的计算结果对比

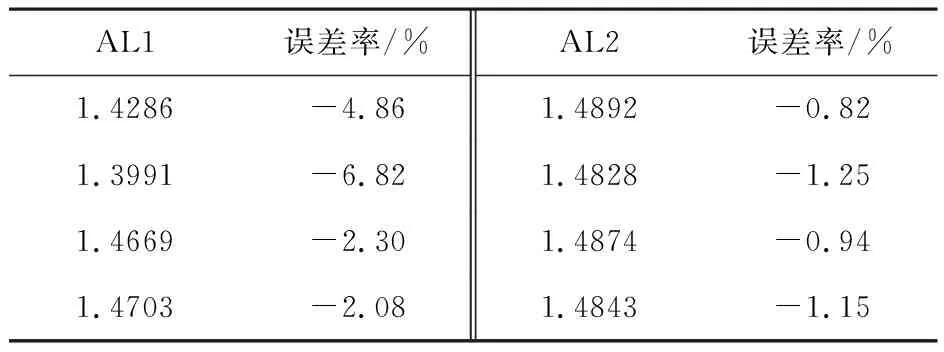
表2 5 000个演化点时小数据量法与模糊C均值小数据量法的计算结果对比

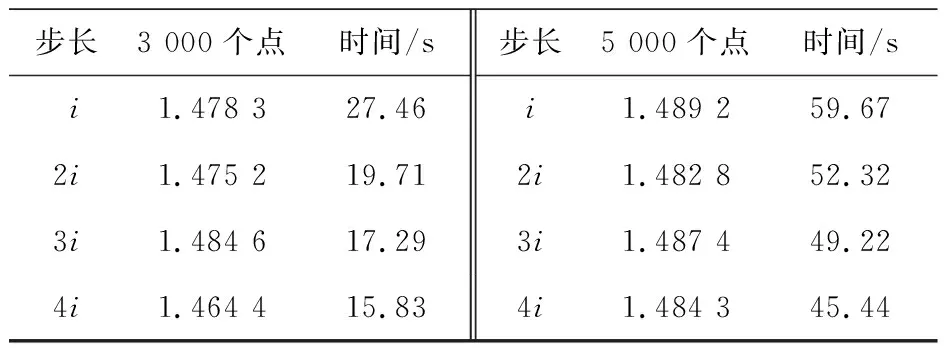
表3 模糊C均值小数据量法改变步长的计算结果1(LLE理论值为1.501 5)

表4 模糊C均值小数据量法改变步长的计算结果2(LLE理论值为0.881 0)

4 结论

将模糊C均值聚类算法用于小数据量法线性区域的选择而提出的模糊C均值小数据量法来计算LLE，通过选出小数据量法的线性区域，可以大大提高小数据量法的计算精度.实验表明，当每次迭代的离散时间步长增加时，计算时间将减少.接下来可以研究离散步长的选取对于实验精度和效率的影响，从而得到更为完善的模糊C均值小数据量法.