宽带相干信号DOA和极化参数联合估计方法

王栗沅, 何华锋, 韩晓斐, 何耀民, 李 震

(火箭军工程大学导弹工程学院, 陕西 西安 710025)

0 引 言

极化作为除时、频、空域外又一类重要的电磁特征,刻画了电场矢量的运动轨迹。利用矢量传感器进行波达方向(direction of arrival, DOA)和极化参数的联合估计,在雷达信号处理领域[1-3]受到广泛关注。均匀圆阵矢量传感器(uniform circular array vector sensor, UCA-VS)能够提供全空域范围内的方位信息和极化信息[4],因此长期以来被作为热点的研究对象。在均匀圆阵的结构下,旋转不变子空间(estimation of signal parameters via rotational inva-riance techniques, ESPRIT)[5-6]和多重信号分类(multiple signal classification, MUSIC)[7-8]等经典的子空间类估计算法因能够获取高精度的参数信息而得到推广应用。文献[9]针对具有交叉偶极子的线阵结构,首次将ESPRIT拓展至极化域。文献[10]利用四阶累积量,将ESPRIT应用在UCA-VS上,实现DOA和极化参数的联合估计。文献[11]提出了降维MUSIC(quaternion-MUSIC, Q-MUSIC) 算法,通过对极化域-空域联合导向矢量的解耦,分离信号的波达角和极化参数,将MUSIC算法中复杂的四维谱峰搜索问题转化为二维谱峰搜索问题,减小了算法的计算量。文献[12]则利用导向矢量和噪声子空间的正交关系估计信号的极化参数,提出了秩亏损MUSIC(rank loss MUSIC, RL-MUSIC)算法,进一步降低算法的复杂度。文献[13]通过构造DOA矩阵方法(DOA matrix method, DMM)估计入射信号参数,此过程无需谱峰搜索,以降低部分估计精度为代价换取计算量的大幅减小。在后续的研究中,学者在估计精度和算法的实时性上进行取舍,提出了许多性能优良的改进算法[14-17]。

以上研究方法多是针对窄带、信号不相关的条件。而在实际的电磁对抗环境下,具有更强的抗截获、抗干扰能力的宽带信号和由多径传播形成的高度相关或相干信号更为普遍。在信号高度相关或相干条件下,阵列接收数据协方差矩阵出现秩亏现象,导致以上估计方法不再适用。空间平滑(spatial smoothing, SS)[18-19]和极化平滑(polarization smoothing, PS)[20-21]等方法为解相干信号提供了有效的手段。文献[22]通过模式空间变化将圆阵变为虚拟线阵,而后进行空间平滑,拓宽了SS的应用范围,但仍无法处理具有极化信息的阵列数据。PS算法通过对阵列数据不同极化分量的加权平均,实现了信号的解相干,但此过程破坏了数据矩阵的极化域结构,无法进一步估计信号的极化信息[23]。文献[13]采用双圆阵的轴向虚拟平移估计二维相干信号,但此方法无法直接估计极化参数且存在阵元损失。另一方面,在宽带背景下,信号的导向矢量与瞬时频率有关,窄带的参数估计方法不再有效。为此,研究者将宽带信号分解为多个窄带信号,提出了基于相干信号子空间方法(coherent signal-subspace method, CSM)的参数估计算法。针对CSM算法中聚焦矩阵的构造问题,目前典型的方法包括双边相关变换[24]、旋转信号子空间[25]和信号子空间变化[26]等,然而以上方法均需要预估角度信息,预估误差对算法精度产生较大影响。文献[27]以阵列自相关矩阵的特征向量作为过渡矩阵,提出了一种不依赖于角度先验信息的聚焦方法,即特征向量信号子空间法(eigenvectors signal subspace, ESS),实现了宽带信号的空间测向。文献[28]则基于宽带循环平稳信号的特有性质,将循环互相关函数分离成独立的方向矩阵和极化旋转矩阵的乘积,以此构造DOA矩阵,进行空间定位和极化估计。

受以上方法启发,本文提出了具有低复杂度的极化DOA矩阵法(polarization DOA matrix method, PDMM),并联合ESS的空间聚焦方法,实现了宽带相干信号背景下DOA和极化参数的联合估计。本文主要做出了以下贡献。

(1) 与文献[13,16-17]不同的是,本文提出了在宽带背景下的轴向虚拟平移解相干方法。该方法将宽带信号分为若干窄频带信号,通过对单一圆阵进行轴向虚拟平移和平滑,有效达到解相干的目的,同时不存在阵元的损失。

(2) 相比于传统的DMM,本文充分利用了各频点下的数据矢量信息,提出了适用于宽带的PDMM。该方法根据聚焦和平滑的思想,将轴向虚拟平移后的自协方差矩阵变化到某一频点下并对互协方差矩阵进行平滑处理,以此构造极化波达方向矩阵。

(3) 对于DOA和极化参数的估计,本文充分利用了极化波达方向矩阵特征值和特征向量信息,通过闭合式求解,有效估计出信号的四维参数,所得参数自动配对。算法无需谱峰搜索,大大降低了计算复杂度,同时该方法最多仅需要3个阵元信息即可有效估计出DOA和极化参数,节约了硬件资源。

1 信号模型

考虑均匀圆阵由M个非完备的电磁矢量传感器组成,其沿切线方向等角度放置在以r为半径的圆周上。每个传感器由3个相互正交的电偶极子组成,电偶极子负责接收入射电磁波的电场分量信息。假定有K个远场、宽带的线性调频完全极化电磁波信号S(t)=[s1(t),s2(t),…,sK(t)]T入射至阵列。记第k个入射信号的俯仰角φk∈[0,π/2];方位角θk∈[-π/2,π/2];极化幅角γk和极化相位差ηk表示信号电场矢量的两个分量,γk∈[0,π/2],ηk∈[-π,π]。进一步地,假设阵元噪声是以0为均值、σ2为方差的高斯白噪声,且与入射信号互不相关。因此,第m个阵元上输出的信号矢量可表征为

(1)

式中:τm(θk,φk)表示第m个阵元接收第k个信号时相对于首个阵元接收的时延。对于宽带信号而言,信号的时延与瞬时频率有关,因此阵列导向矢量数据无法直接在时域上体现。现将一段在足够长的观测时间内采集到的信号分为L个子段,对每个子段的接收信号进行I点的离散傅里叶变换,得到阵列输出的频域模型X(fi)=[X1(fi),X2(fi),…,XL(fi)],其中L同时代表频域快拍数,第l个子段中频点fi处的阵列数据频域模型Xl(fi)可表示为

Xl(fi)=A(fi,θ,φ,γ,η)Sl(fi)+Nl(fi)

(2)

记i=1,2,…,I代表频率范围,Sl(fi)=[s1(fi),s2(fi),…,sK(fi)]T表示K维的相干信号矢量;Nl(fi)表示3M维的观测噪声矢量;A(fi,θ,φ,γ,η)表示频点fi处的导向矢量

(3)

a(fi,θk,φk,γk,ηk)=as(fi,θk,φk)⊗

ap(fi,θk,φk,γk,ηk)

(4)

式中:as(fi,θk,φk)=[as,1,as,2,…,as,M]T表示第k个信号的空域导向矢量;ap(θk,φk,γk,ηk)表示第k个入射信号的极化域-空域导向矢量;⊗表示Kronecker积。

(5)

ap(θk,φk,γk,ηk)=HE=

(6)

式中:λk表示第k个信号的波长;ap表示三通道的极化域-空域导向矢量,由坐标转化矩阵H和极化相位描述子E组成。

2 模型预处理

2.1 平滑和降噪

在实际复杂的电磁环境中,空间多径效应的存在往往导致接收信号的自相关矩阵出现降秩情况,难以有效进行后续参数的估计与分析。为此,采用轴向虚拟平移对阵列接收信号进行解相干处理[16]。

假设阵列以d=λ/2为移动间距沿载体运动方向虚拟平移P次,如图1所示。

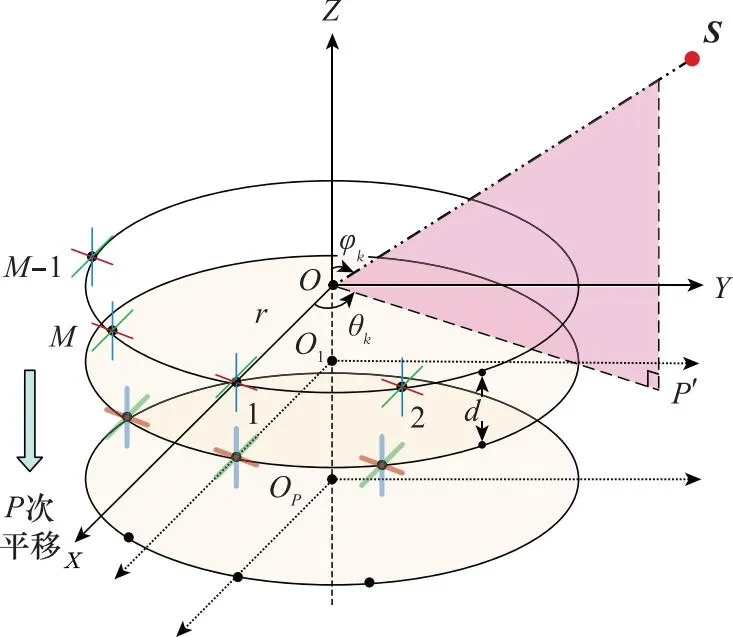
图1 阵列虚拟平移示意图Fig.1 Schematic diagram of array virtual shift

平移后,在每个频点fi下可得到一组虚拟阵列接收数据X(p)(fi):

X(p)(fi)=A(fi,θ,φ,γ,η)Φ(p)(fi,φ)S(fi)+N(fi)

(7)

式中:p表示虚拟平移的次数,满足0≤p≤P;Φ(p)(fi,φ)为空间相位差矩阵。

(8)

该频点处的自协方差矩阵和互协方差矩阵可表示为

(9)

式中:RS(fi)=S(fi)SH(fi)。对式(9)进行空间平滑,得到平滑后的协方差矩阵为

(10)

(11)

在此基础上,对自协方差矩阵和互协方差矩阵进行降噪处理,得到在单频点下的去噪协方差矩阵:

(12)

2.2 空间聚焦

经上述分析,得到了各频点下接收数据的自协方差矩阵和互协方差矩阵,这其中蕴含着信号的方位信息和极化信息。但如果直接使用各频点下的协方差矩阵进行DOA和极化参数估计,由于其并不是在同一个参考点上测量的,因此计算结果会有偏差。为了解决这一问题,需要将各频点下的信号空间“聚焦”到同一参考频点上[29]。

经平滑和降噪处理后,各频点下的自协方差矩阵为Hermitian矩阵,对其进行特征分解:

(13)

(14)

s.t.T(fi)TH(fi)=I

(15)

文献[27]证明T(fi)满足以下关系:

T(fi)=U(f0)UH(fi)

(16)

从式(16)可以看出,聚焦矩阵的求解只需要对各频点接收信号自协方差矩阵进行特征分解,利用其对应的特征向量即可实现。经聚焦和平滑处理后的自协方差矩阵可表示为

(17)

3 所提算法

本节提出了一种低复杂度的DOA和极化参数估计方法——PDMM。算法在模型预处理基础上,首先利用聚焦后的自协方差矩阵和平滑后的互协方差矩阵构造极化波达方向矩阵,然后利用该矩阵特征值估计俯仰角,利用特征向量和导向矢量的关系进一步估计方位角和极化角,算法总体流程如图2所示。

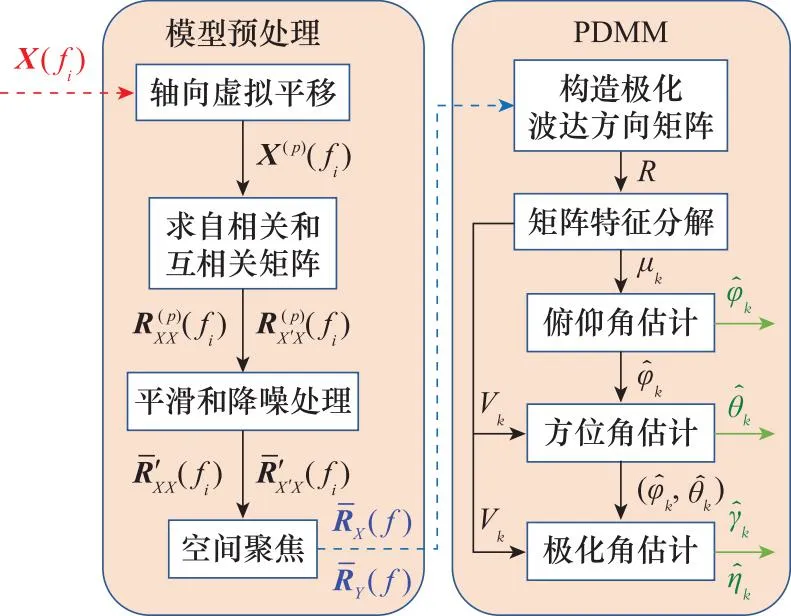
图2 算法总体流程Fig.2 Overall flowchart of the proposed algorithm

3.1 波达方向估计

经聚焦后得到参考频率f0处的自协方差矩阵。进一步,对各频点处的互协方差矩阵进行平滑处理:

(18)

定义极化波达方向矩阵:

(19)

(20)

文献[30]证明R满足以下关系:

RA(f,θ,φ,γ,η)=A(f,θ,φ,γ,η)Φ(f,φ)

(21)

分析式(21),R的K个较大特征值与Φ中对角线元素相对应。另一方面,通过式(8)可知,Φ又是由俯仰角φ唯一确定的。因此,通过R的特征值可以估计出目标信号的俯仰角:

(22)

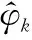
另一方面,极化波达方向矩阵R同时满足:

RV1:K=V1:KΦ

(23)

式中:V1:K表示R的K个较大特征值所对应的特征向量矩阵。比较式(21)和式(23)可以看出,特征向量矩阵V1:K与导向矢量A线性相关,V1:K中包含入射信号的方位信息和极化信息。

(24)

(25)

因此,对于第k个信号3M×1维的导向矢量Ak,满足:

(26)

由式(26)可知,不同阵元间同一极化通道上导向矢量数据的差异源于空域导向矢量as,m的差异。由式(5)可知,这个差异来源的本质是由俯仰角和方位角共同决定的。因此,在估计出俯仰角的基础上,利用相邻阵元间空域导向矢量的差异即可实现对方位角的估计。考虑到阵元2和阵元1存在2π/M的角度差,阵元M和阵元1存在-2π/M的角度差。根据式(5),定义中间变量t:

(27)

(28)

由式(28)估计的方位角,能够保证[-π/2,π/2]上的无模糊估计。

3.2 极化参数估计

在得到俯仰角和方位角参数的基础上,空间旋转矩阵H可表示为

(29)

(30)

(31)

(32)

经上述分析,相干信号的DOA和极化参数能够依据极化波达方向矩阵的特征值和特征向量计算得到,参数一一对应。下面给出本文算法的具体步骤。

步骤 1对原阵列进行轴向虚拟平移,得到平移后各频点下的阵列接收数据X(p)(fi)。

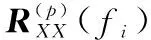
步骤 5对各频点处的互协方差矩阵进行平滑,根据式(19)构造极化波达方向矩阵R。

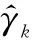
4 实验分析

仿真实验从算法复杂度、有效性和稳健性3个层面来考察所提方法的性能。

4.1 复杂度分析

所提的PDMM充分利用极化波达方向矩阵的特征值和部分特征向量信息,通过闭合式求解得到DOA和极化参数的估计值,此过程无需进行谱峰搜索,因此具有较低的计算复杂度。为了充分说明所提算法的优势,将与3种子空间类超分辨经典算法Q-MUISC[11]、RL-MUISC[12]和ESPRIT[10]进行比较分析。

宽带相干信号条件下的DOA和极化参数估计算法主要分为3个步骤:一是信号的解相干处理;二是矩阵的聚焦,将宽带各频点的接收矢量聚焦到参考频点处;三是利用不同算法实现参数估计。本文中所对比的算法采用了相同的矩阵聚焦方法,不同之处在于信号解相干的实现算法和参数估计算法。

现假设两类算法阵元个数为M,相干信号个数为K,快拍数为L,谱峰搜索个数为N。本文算法在信号解相干处理过程中的运算量主要集中在求解自相关、互相关矩阵上,此计算量为O{2L(3M)2},进行矩阵特征分解的计算量为O{(3M)3},估计DOA和极化参数的计算量为O{9K}。因此,算法总计算量为O{2L(3M)2+(3M)3+9K}。

下面对3种对比算法的复杂度进行分析。

Q-MUSIC算法[11]首先利用极化平滑[20]进行信号的解相干处理,该过程计算量主要集中在自相关矩阵的求解上,此计算量为O{3LM2};然后利用子空间降维的思想,构造二维空间谱,实现DOA和极化参数分步估计,该过程计算量集中在矩阵特征值分解和谱峰搜索上,计算量分别为O{M3}和O{N2(8M3+1+K(M3+1))},因此文中Q-MUSIC算法的总计算量为O{3LM2+M3+N2(8M3+1+K(M3+1))}。

RL-MUSIC算法[12]与Q-MUSIC算法的区别在于极化参数的估计,在DOA参数的基础上,利用导向矢量和噪声子空间正交的关系估计信号的极化参数。该过程计算量集中在广义特征分解上,计算量为O{K(27M3+2)},因此,RL-MUSIC算法的总计算量为O{3LM2+M3+N2(8M3+1)+K(27M3+2)}。

ESPRIT算法[10]首先构造四阶累计量,需要进行27L·(M2+2)次复数乘法;然后基于旋转不变子阵列构造旋转不变矩阵,此过程复杂度集中在矩阵的奇异值分解上,计算量为O{14(M2+2)(K+2)+(M2+2)2(K+2)/2};最后利用总体最小二乘法求解该矩阵,并进行波达角和极化角的参数配对,此计算量为O{14K2+(M2+2)K2/2+3K2(K+2)+2K3}。

为更直观地展示对比结果,以柱状图的形式描述不同阵元数条件下算法的计算复杂度。在仿真中,假设有3个相干信号入射至阵列,信号的频域快拍数为1 024,MUSIC算法进行的二维DOA谱峰搜索假定以1°为步长在(0,90°]范围内进行,结果如图3所示。从图3能够直观地看出,本文所提算法相比经典MUSIC算法在计算复杂度上具有显著优势,与ESPRIT算法相比,本文算法也具有更低的计算复杂度。这在对导弹武器测向定位这类实时性要求较高的应用场景中具有一定参考价值。

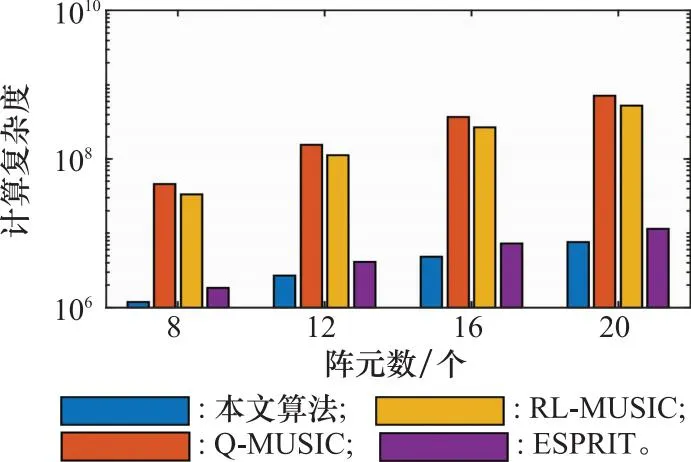
图3 不同算法计算复杂度对比示意图Fig.3 Comparison diagram of computational complexity of different algorithms

4.2 有效性分析

文中算法的有效性是检验在相干信号条件下算法的正确性。仿真中,阵列阵元数M=10,均匀圆阵的半径r=λ/2,轴向平移间距d=λ/2,信号采样频率fs=24 GHz,快拍数L=1 024,假设三正交偶极子中的噪声遵从高斯分布且信噪比SNR=15 dB。

仿真 1平滑和聚焦的有效性

图4 模型预处理结果Fig.4 Model preprocessing results

仿真 2参数估计的散点图

此部分实验验证的是所提PDMM参数估计的有效性。实验参数同仿真1所设置参数保持一致。200次独立蒙特卡罗仿真实验结果如图5所示。从图5可以看出,本文方法能有效分辨两个相干信号的来波方向。这一方面进一步说明了轴向虚拟平移技术能够实现相干源的解相干处理;另一方面也验证了所提参数估计算法能够有效估计出信源的DOA和极化参数。

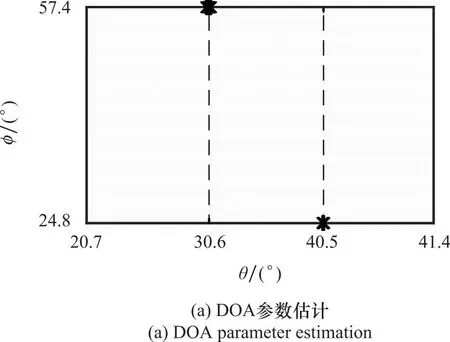
图5 两个相干信号参数估计散点图Fig.5 Scatter points diagram of parameter estimation of two coherent signals

4.3 稳健性分析

算法的稳健性是指在不同指标下所提算法性能的稳定性。仿真从信噪比、快拍数、阵元数3个维度来考察算法的稳健性,通过均方根误差(root mean square error, RMSE)来定量刻画3类指标的变化对算法性能的影响。RMSE定义如下:

(33)

式中:N表示蒙特卡罗仿真的次数;zk表示第k个信号的某一角度参数的真实值;znk表示第n次蒙特卡罗仿真中第k个信号某一角度参数的估计值。

为更好地描述与分析,对信号和阵列做出如下设定:不失一般性地,假设有两个相干信源入射到UCA-VS中,两个入射信号载频f=1 GHz,带宽B=0.5 GHz,脉宽T=12 μs,两个信号的波达方向参数(θ,φ)分别为(20°,60°)和(30°,40°),极化参数(γ,η)分别为(10°,20°)和(50°,10°);阵列由M个三正交的电偶极子组成,圆阵的半径R=Md/2π,其中d=λ/2表示阵列轴向虚拟平移的间距,信号采样率fs=24 GHz,快拍数为L。

仿真 3不同信噪比下算法稳健性

DOA参数和极化参数的RMSE随信噪比变化的曲线如图6所示。仿真中,假定M=8,L=1 024,SNR=5∶3∶23,进行200次独立的蒙特卡罗实验。从整体上看,相干信号DOA参数估计的RMSE要小于极化参数的估计误差,测向精度在低信噪比环境下仍能取得较准确的结果,基本满足雷达导引头在复杂电磁环境下的测向要求。从单个参数着手,俯仰角的估计值是通过极化波达方向矩阵的特征值计算得到的,因此具有较好的稳健性;方位角的估计是在俯仰角估计的基础上进行的,误差存在一定的累积。这种积累伴随着空间旋转矩阵H作用到了极化参数的估计上。因此,在低信噪比下误差积累相对较大。

为更全面掌握算法在不同信噪比下的性能,将本文算法与Q-MUSIC、RL-MUSIC和ESPRIT这3种超分辨算法进行对比分析,进行200次独立的蒙特卡罗仿真实验,结果如图7所示。由图7可以看出所提算法与Q-MUSIC、RL-MUSIC算法DOA参数的估计精度相仿,但极化参数估计误差较大。这是由于本文算法的极化估计是经闭式求解得到的,这种方式虽然大大减小了计算复杂度,但在估计过程中存在一定的误差累计,导致估计精度稍差。此外,基于ESPRIT算法的DOA和极化参数估计精度都呈现出较大的动态变化,尤其在低信噪比条件下,性能急剧恶化。显然,对比之下,本文算法较ESPRIT算法更具优势。

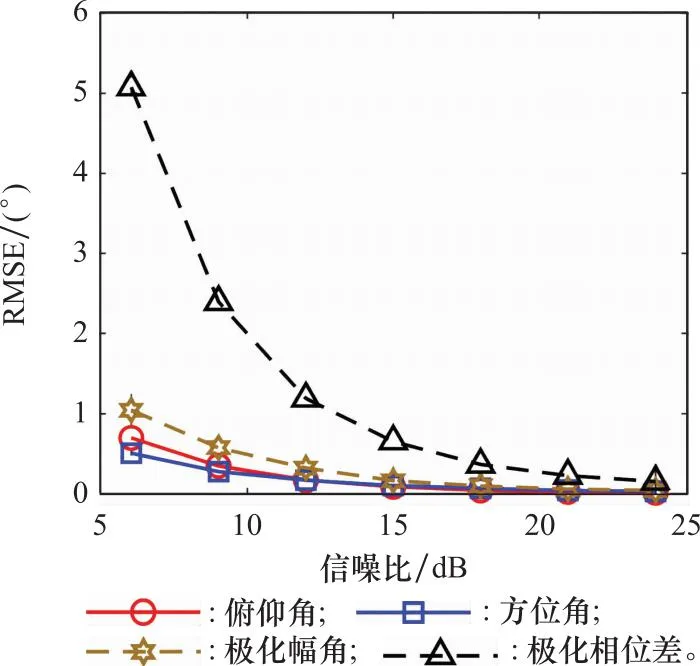
图6 RMSE随信噪比变化曲线图Fig.6 Variation curve of RMSE with SNR

图7 不同算法随信噪比变化性能曲线Fig.7 Performance curves of different algorithms with SNR variation

仿真 4不同快拍数下算法稳健性

从前文分析可知,RL-MUSIC算法相比Q-MUSIC算法具有更低的计算复杂度,相比ESPRIT算法具有更高的估计精度。因此,在下面的仿真中,着重将本文算法与RL-MUSIC算法进行对比分析。

两种算法的RMSE随快拍数变化的性能曲线如图8所示。仿真中,M=8,SNR=15,L=128∶128∶1 024,利用MUSIC进行谱峰搜索时设置步长为1°,进行200次独立的蒙特卡罗仿真实验。从图8可以看出,本文算法相比对比算法更加稳定,在低快拍条件下,对比算法呈现出较大的动态变化。究其原因,对比算法的估计精度很大程度上与接收数据矢量的维度有关。维度越大,接收数据矩阵所含信息就越丰富,估计精度就会越高;而本文算法利用轴向虚拟平移解相干信号,本质上是对阵列数据的同相叠加,提高了信噪比,因此具有较好的稳健性。

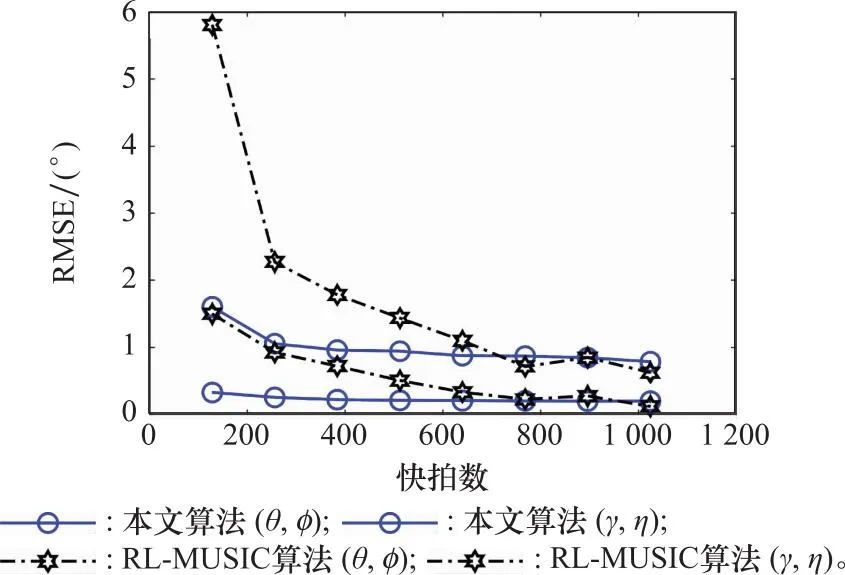
图8 RMSE随快拍数变化曲线Fig.8 Variation curve of RMSE with number of snapshot

仿真 5不同阵元数下算法稳健性

阵元数通过影响接收数据的协方差矩阵进而影响算法的性能。仿真中,假定SNR=15,L=1 024,M=4∶2∶16,经200次独立蒙特卡罗仿真的实验结果如图9所示。由图9可以看出,本文算法的RMSE相比RL-MUSIC算法更加稳定,尤其是在阵元数M≤6时,所提算法仍取得较好的估计性能,而对比算法的估计误差明显增大。分析原因,对比算法对数据的协方差矩阵进行了高精度的谱峰搜索,更充分地利用了阵元信息,然而在阵元数较少的情况下,阵列误差对算法的影响更为显著。而本文算法在进行波达角估计时仅利用了3个阵元的信息,在进行极化参数估计时,仅利用了1个阵元信息,通过对少量阵列数据的闭式求解,有效估计出各参数。因此,在阵元数较少的情况下,所提算法更具优势,能够节约硬件资源。

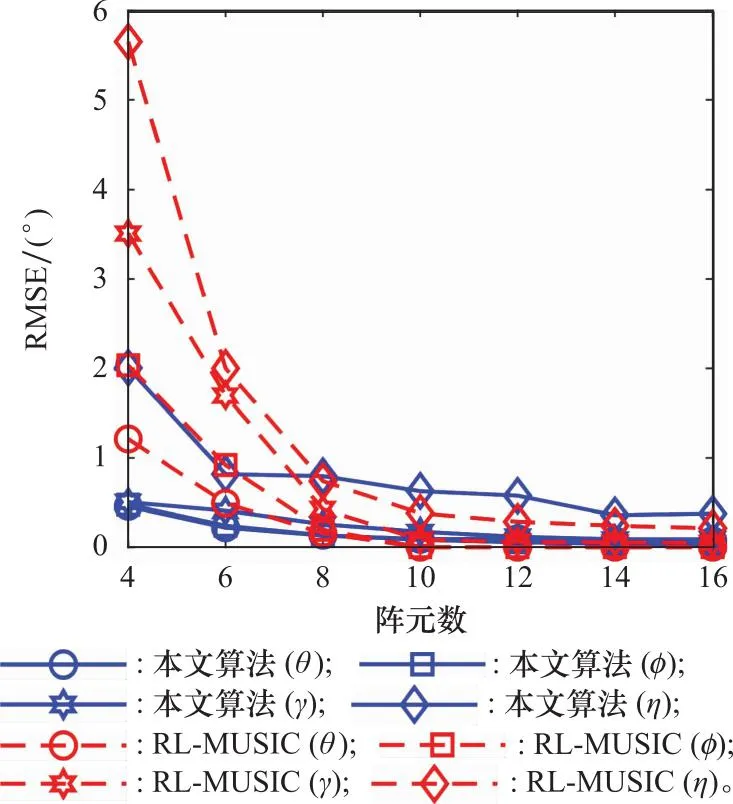
图9 RMSE随阵元数变化曲线Fig.9 Variation curve of RMSE with array elements number

5 结束语

本文联合特征向量子空间的聚焦方法,提出了一种适用于宽带相干信号条件的DOA和极化参数联合估计方法。该算法通过轴向虚拟平移和空间聚焦,构造极化波达方向矩阵,利用该矩阵的特征值和特征向量信息估计出入射信号DOA和极化参数,并实现了参数的自动配对。该方法无需谱峰搜索,大大降低了计算复杂度,在低快拍下仍能保持良好的估计性能,基本满足了雷达导引头对测向实时性和估计精度的要求。同时,算法仅需3个阵元信息即可估计出信号波达角和极化角,能够节约硬件资源。但也应该注意到,该算法对信噪比的要求较高,在低信噪比条件下极化参数估计误差较大,因此提高估计算法在低信噪比环境下的估计性能是下一步工作的重点。