基于布谷鸟搜索算法的机动化箔条幕布放方法研究

裴立冠, 周 唯, 刘经东

(中国人民解放军91550部队, 辽宁 大连 116023)

0 引 言

在现代海战场环境中,针对来袭飞行器实施有效干扰对于保证水面舰艇自身安全和战斗力具有重要意义,箔条弹作为一种无源干扰方式,具备成本低、使用简便、可从雷达主瓣干扰等优势,是有效防御主动雷达制导型飞行器的重要手段[1-3]。但是,伴随动目标显示、边搜索边跟踪等雷达抗干扰技术在导引头中的应用,传统质心、冲淡和幕墙式箔条干扰方法的干扰效能逐渐降低[4-6]。因此,有必要提出一种新的箔条弹干扰布放方法,以有效应对新型飞行器威胁。

从公开资料来看,目前已经积累了一些关于箔条弹干扰布放的研究成果。其中,一部分学者基于协同理念,将箔条弹布放与有源干扰或自身平台机动相结合,探索提升干扰效果的方法。如文献[7-9]均提出有源压制干扰与箔条无源干扰的协同干扰方法,通过干扰波束直接照射箔条云,以增强针对雷达主瓣的干扰能力;文献[10]探索了有源欺骗干扰与箔条质心干扰的组合使用方法,并提出具体干扰原则;文献[11-12]分别研究得到直升机机动、舰艇机动与箔条弹布放的协同方案。综合而言,上述研究成果在一定程度上规避了传统箔条干扰弊端,但由于其对协同双方在空间和时间配合上要求很高,因此在复杂战场环境中可实施性有待商榷。

另一部分学者提出了箔条幕干扰的思路,通过在飞行器来袭方向一次性投放数枚箔条弹,对舰船目标形成大面积幕墙式的有效遮蔽。如文献[12]对箔条幕防御飞行器进行了原理论证与作战仿真研究;文献[13]探索了大气环境下箔条运动轨迹特性,建立了箔条幕扩散模型;文献[14]以边搜索边跟踪末制导飞行器为干扰对象,研究了针对性的箔条幕布放方法。总体来说,此类箔条幕干扰方法具有较强的可实施性,但由于幕墙为预先一次性布放,对抗过程中幕墙形态仅受风影响,容易被雷达导引头识别和抗干扰,即使有后期箔条弹补放措施,其布放平台也为被保护目标本身,一旦时机掌握不够科学,容易暴露目标,起到相反效果。

为此,提出一种通过无人机和舰船平台协同布放箔条弹形成箔条幕干扰的方法,拟在保持原始箔条幕干扰优势的基础上,基于改进的布谷鸟搜索算法以控制箔条弹布放速率和方向,使幕墙能量质心随时间增长不断移动,有效应对雷达导引头抗干扰技术,并保证舰船成功逃逸。具体而言,通过分析机动化箔条幕干扰机理,构建箔条幕布放模型,据此提出总体思路,并建立布放效能条件、采用Logistic混沌机制改进布谷鸟搜索算法、建立补弹策略,最终通过实际案例仿真分析验证所提方法的有效性。

1 干扰机理分析

如图1所示,机动化箔条幕干扰的实质为:综合考虑飞行器主动雷达导引头、自然环境等特征要素,借助无人机和舰船协同完成对多枚箔条弹的可控化逐枚布放,形成一条具有足够长宽高、轴线与初始弹目方向基本垂直且能量质心按照既定规律不断移动的箔条幕墙,以保障幕墙另一侧舰船成功逃离飞行器雷达导引头跟踪。具体实现以下两种功能:① 遮蔽功能,利用箔条幕衰减飞行器雷达导引头发射的电磁波和舰艇反射的电磁波,使雷达导引头无法有效跟踪幕墙另一侧舰船目标,转而跟踪幕墙能量质心;② 质心拖引功能,通过控制无人机与舰船的箔条弹布放位置与时机,使幕墙能量质心逐步远离舰船目标,并欺骗雷达导引头跟踪波束随幕墙能量质心不断移动,最终达到飞行器起爆时刻舰船逃离雷达导引头跟踪波束和杀伤半径的目的。基本实现方法为:① 无人机与舰船协同布放箔条弹,采用舰船与无人机(图1舰船S和无人机P)基本背向机动方法,其中舰船行驶速度为vS,其布放箔条弹主要用以遮掩舰船目标,初次布放的箔条弹C11位于初始时刻弹目线上,与舰船距离为h;无人机与舰船机动方向基本相反,飞行速度为vA,其布放箔条弹主要用以达到随时间增长幕墙质心与舰船间距离逐渐增大要求;② 箔条弹布放方向协同控制,幕墙受风速风向影响会随时间不断运动,为保证多枚箔条弹始终处于同一轴线,需根据无人机速度、舰船速度与风速、风向之间的关系,对箔条弹布放方向进行控制;③ 相邻箔条弹间布放距离,假设单枚箔条弹完全散开后,电磁波有效反射面为半径为R的圆形,为保证幕墙无明显间隔,任意时刻相邻箔条弹间距离需小于2R;④ 箔条幕轴线方向H2基本垂直于初始弹目轴线M0S0,图1中H1为M0S0垂线,α为H2相对于H1的偏转角。

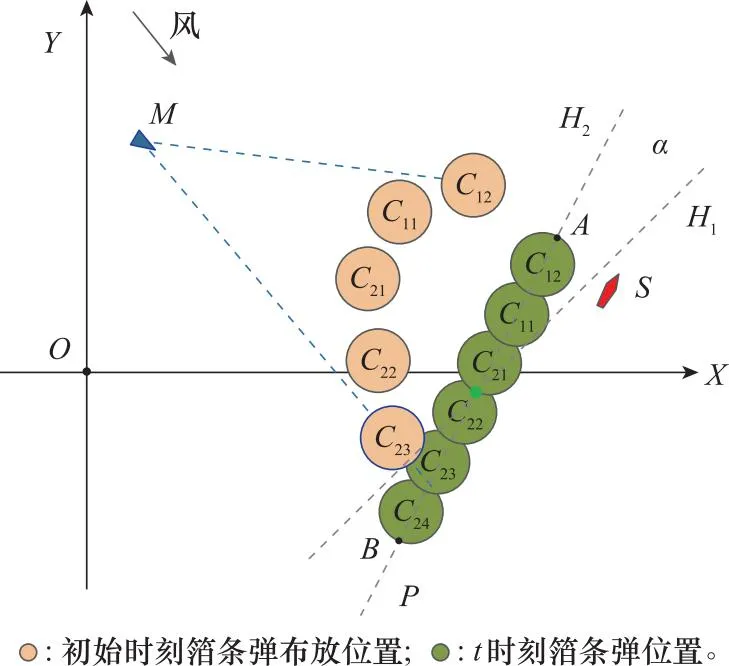
图1 机动化箔条幕干扰原理示意图Fig.1 Schematic diagram of mechanized chaff screen interference

为后续建模分析方便,做出如下定义:① 定义舰船方发现飞行器为初始时刻,且舰船与无人机立即开展箔条幕布放;② 暂不考虑无人机从起飞位置抵达初始布放位置以及无人机返航消耗的飞行时间和路径资源;③ 由于雷达导引头在跟踪过程中距离海面高度较低,因此将雷达导引头、无人机、箔条幕、舰船视为一个平面;④ 以初始时刻雷达导引头质心M所在正北方向为Y轴,顺时针旋转90°且过舰船质心S的线为X轴,坐标原点O及坐标系如图1所示;⑤ 定义箔条弹布放速率参数,其中舰船S布放箔条弹速率为v1,其大小为舰船布放的相邻两枚箔条弹距离与时间差的比值,而无人机A箔条弹布放速率v2等于其飞行速率vA;⑥ 定义雷达导引头在跟踪过程中始终采用比例导引法修正航线[15-17];⑦ 模型中涉及到的所有角度均采用统一定义,与X轴正向平行角度为0°,逆时针旋转角度不断增大。

2 布放模型构建

2.1 雷达导引头运动模型

(1)

式中:[Mx(t),My(t)]表示t时刻雷达导引头M的位置坐标;vm表示雷达导引头攻击速率;Bm(t)表示t时刻雷达导引头攻击方向与基准线夹角;Δt表示t-1时刻与t时刻的时间差值。

2.2 舰船运动模型

(2)

式中:[Sx(t),Sy(t)]和[Sx(0),Sy(0)]分别表示舰船S在t时刻和初始时刻的坐标位置;ωS表示舰船机动角度;β表示舰船初始机动角度;Δβ表示舰船机动转角[18]。

2.3 箔条幕形态模型

根据实际布放经验,单发箔条弹完全散开后,宽度和厚度在有效干扰时间段内始终能够满足箔条幕遮蔽要求[12],因此在分析箔条幕形态时,主要讨论单发箔条弹平均有效反射面积、有效半径以及整个幕墙有效长度。

(1) 由文献[7]的分析可知,综合考虑互耦效应及箔条损坏因素,单发箔条弹完全散开后的平均有效反射面积σN如下所示:

(3)

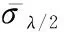
(2) 单发箔条弹完全散开后的平均有效反射半径R如下所示:

(4)

(3)t时刻箔条幕墙长度LC(t)如下所示:

(5)

2.4 箔条幕运动模型

基于机动化箔条幕干扰机理,构建箔条幕运动模型需要分两步进行,第1步是根据对抗场景,判断舰船与无人机基本机动方向,第2步是建立舰船与无人机机动参数模型。

(1) 基本机动方向判定

为使舰船尽快远离箔条幕质心,舰船机动方向应与箔条幕质心变化方向基本相反,为此综合考虑舰船与雷达导引头位置、风向及箔条幕偏转角度,得到舰船与无人机基本机动方向,具体关系如下所示。

(6)

(2) 箔条弹布放间隔

图2(a)和图2(b)分别为图1对抗场景下舰船和无人机布放箔条弹示意图。其中,vW表示风速,φ1和φ2分别表示两个平台布放箔条弹方向与箔条幕轴法线方向的夹角。

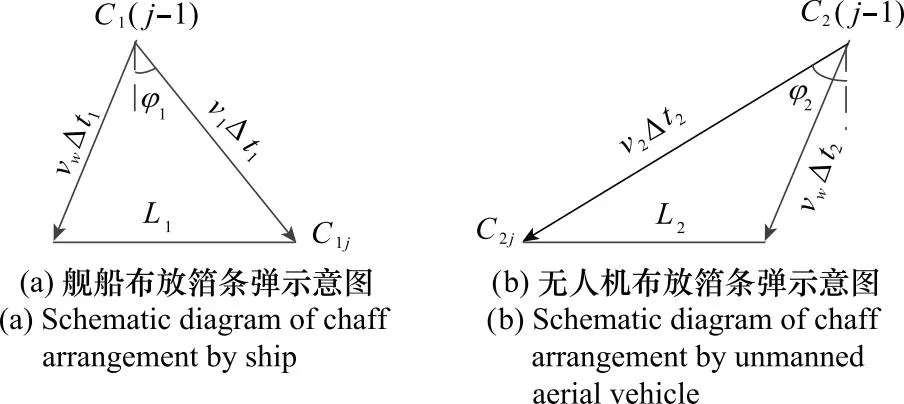
图2 相邻箔条弹布放示意图Fig.2 Schematic diagram of adjacent chaff arrangement

对各类对抗场景分析得到,舰船和无人机布放两枚相邻箔条弹时间差Δt1和Δt2计算方法如下所示:

(7)

式中:φ在不同对抗场景下大小不同。当My(0)>0且Sx(0)>0时,φ=ωW-γ-α-π;当My(0)>0且Sx(0)<0时,φ=-ωW-γ+α+π;当My(0)<0且Sx(0)<0时,φ=ωW+γ-α;当My(0)<0且Sx(0)>0时,φ=-ωW-γ+α+2π。

进一步得到箔条弹布放间隔Li计算方法如下所示:

Li=viΔti,i=1,2

(8)

式中:i取1和2时,分别表示舰船与无人机箔条弹布放间隔。

(3) 箔条弹布放方向

舰船与无人机的箔条弹布放方向φ1和φ2计算方法如下所示:

(9)

(4) 箔条弹布放个数

箔条弹布放个数计算方法如下所示:

(10)

式中:n(t)为箔条弹布放总个数;n1(t)和n2(t)分别表示t时刻舰船和无人机布放的箔条弹个数。

若t时刻对雷达导引头干扰成功,则结合箔条弹布放间隔参数,可得到无人机飞行持续时间T如下所示:

T=[n2(t)-1]Δt2

(11)

(5) 箔条弹初始布放位置

C11和C21初次布放位置:

(12)

其他箔条弹初次布放位置:

(13)

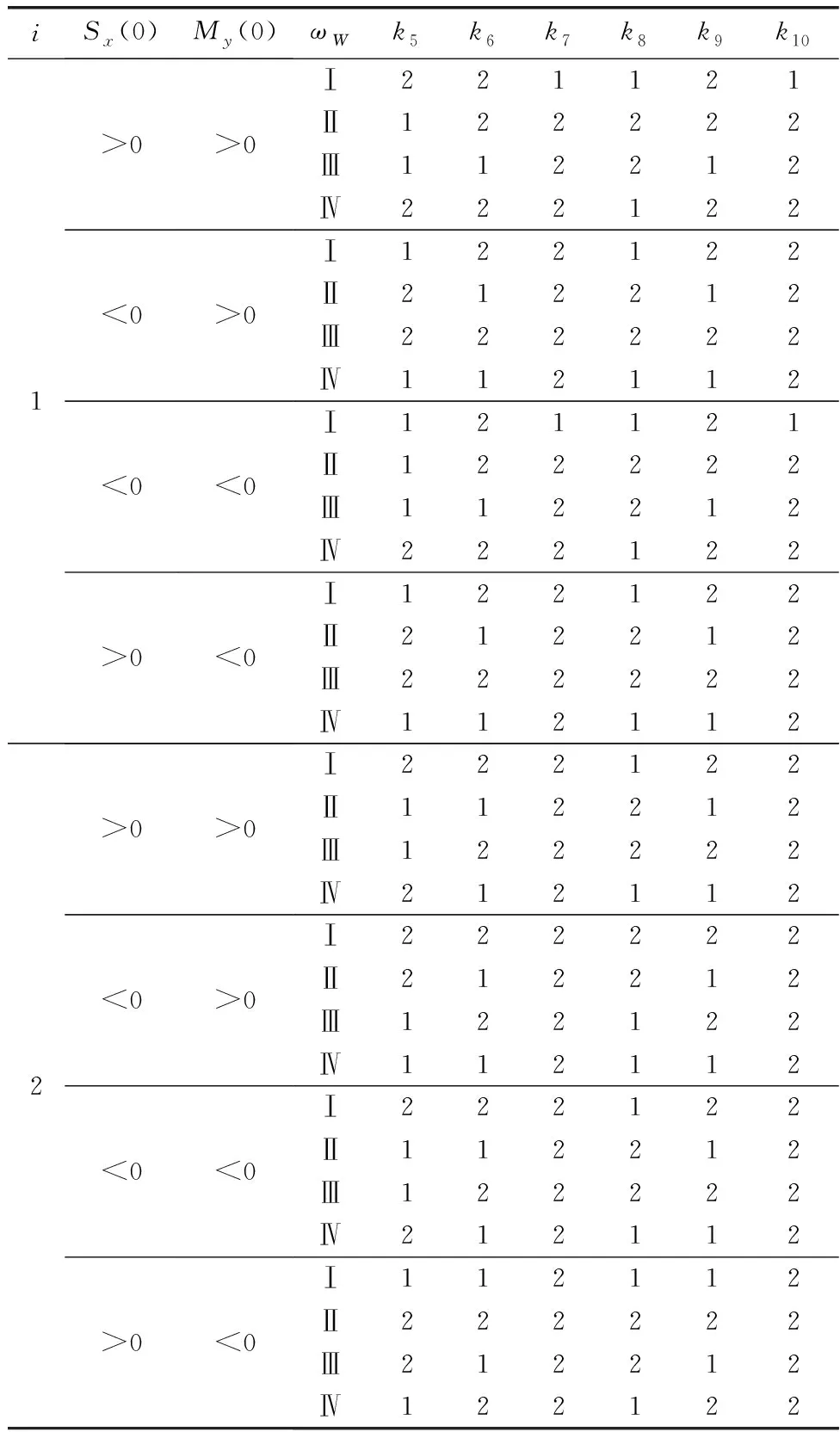
表1 k5～k10赋值Table 1 Assignment of k5-k10

(6) 箔条弹实时位置坐标

(14)

(7) 箔条幕质心坐标

(15)

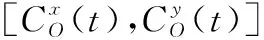
(8) 箔条幕边缘点坐标

(16)

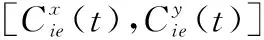
3 求解模型构建

3.1 总体思路

机动化箔条幕干扰模型求解为典型的最优化问题,本研究采用布谷鸟智能优化算法对其进行布放方案求解,结合实际对抗干扰场景,最终确立了总体求解思路,基本流程如图3所示。

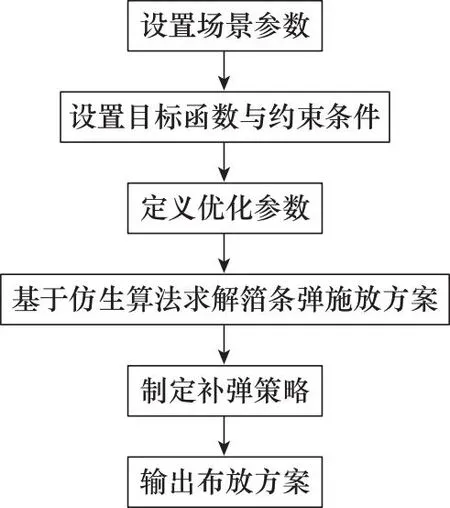
图3 布放方案求解流程Fig.3 Solution flow of arrangement scheme

步骤 1根据实际干扰情景,设置场景参数,包括雷达导引头与舰艇的初始时刻位置坐标、单发箔条弹的箔条根数,反舰导弹雷达导引头电磁波波长、相邻箔条弹间距离、风向与风速等。

步骤 2定义优化参数,由第2.4节箔条幕运动模型可知,除步骤1中实际场景参数外,舰船与无人机箔条弹布放速率v1与v2、舰船布放首发箔条弹C11位置距离舰船初始位置距离h、舰船机动角度Δβ、箔条幕偏转角度α这5个参数均为元参数,即无法由场景参数推导得出,且对箔条弹布放位置与干扰成功率具有直接影响,因此定义上述5个参数作为基本的仿生智能求解优化参数,并根据实际对抗场景设定优化参数上界与下界。

步骤 3设置布放效能条件,包括目标函数与约束条件。其中,目标函数为综合考虑干扰有效性和资源消耗性所设置的优化目标,约束条件为干扰成功的判断条件,具体包含遮蔽有效性约束条件、拖引有效性约束条件、作战资源损耗约束条件和发射能力约束条件。

步骤 4将上述场景参数、优化参数、布放模型、布放效能条件融入改进的布谷鸟搜索算法中,求取最佳布放方案。

步骤 5箔条弹补弹,当初始时刻雷达导引头与舰艇距离较大时,容易出现由于初始箔条幕持续扩散,最终无法有效衰减电磁波到指定程度,从而暴露舰艇目标的现象,此时需要在箔条幕失效前进行补弹。同时,由于补弹过程耗能较大,因此所构设的箔条幕布放方案应尽量较少补弹次数,本研究将该因素融入目标函数设置中。

步骤 6输出布放方案。

3.2 布放效能条件

3.2.1 目标函数

机动化箔条幕布放的目标函数如下所示:

(17)

式中:f表示目标函数值;fL表示箔条幕墙能量质心C与舰船质心S的距离表征函数;LAC表示t时刻箔条幕边缘点A与其能量质心C构成的向量;LCS表示t时刻箔条幕能量质心C与舰船S构成的向量;fh表示无人机飞行损耗,V2t表示箔条弹布放过程中无人机飞行距离;lmax表示无人机可飞行最长距离;fSC表示舰艇方箔条弹损耗;n1sum和n1max分别表示舰艇箔条弹释放量和其装配箔条弹数量;fAC表示无人机方箔条弹损耗;n2sum和n2max表示无人机箔条弹布放数量和其装配箔条弹数量;λ1、λ2、λ3和λ4分别表示fL、fh、fSC和fAC的权重系数,且有λ1+λ2+λ3+λ4=1;gsum表示对抗过程中箔条弹补弹总次数。

3.2.2 约束条件

(1) 遮蔽有效性约束条件

在整个干扰过程中,雷达导引头与舰船始终处于箔条幕两边,且舰船始终被箔条幕有效遮掩从而无法被雷达导引头发现时,判定为遮蔽有效,具体下所示:

(18)

(19)

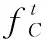
(2) 拖引有效性约束条件

拖引有效性是指,在雷达导引头所在飞行器起爆时刻,舰船成功逃离雷达导引头跟踪波束和飞行器杀伤范围,分别如式下所示:

(20)

(21)

式中:θM表示雷达导引头跟踪波束角度;LMC表示起爆tb时刻M到箔条幕边缘点B构成的向量;LMS表示起爆tb时刻M到S构成的向量。

(3) 作战资源损耗约束条件

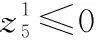
该约束条件包括箔条弹消耗约束条件和无人机飞行约束条件,分别如下所示:

(22)

z6=v2t-lmax≤0

(23)

(4) 发射能力约束条件

该约束条件表示舰船发射每发箔条弹距离均需小于最大可发射距离,如下所示:

(24)

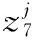
3.3 改进的布谷鸟搜索算法

布谷鸟搜索算法(cuckoo search algorithm, CSA)模拟布谷鸟搜寻最优宿主鸟巢产蛋行为,通过建立莱维飞行公式(式(25))更新种群个体,模型简单、算法参数少且寻优能力较强[19-21]:

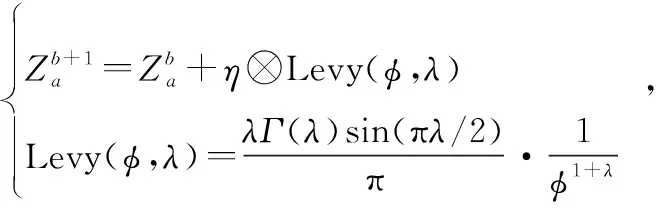
(25)

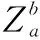
但该算法也存在种群个体更新时采取随机生成模式,容易导致迭代过程中算法陷入局部最优等问题。为此,本研究采取混沌机制对CSA进行改进[25-27],借助混沌机制遍历性和初值敏感性优势,提高算法跳出局部寻优的能力,以用于机动化箔条幕墙干扰问题求解。具体主要针对算法中种群个体生成环节,将初始随机生成样本采用Logistic混沌机制:

yiter1=μ·yiter1-1(1-yiter1-1)

(26)

进行iter1次迭代[28-29],产生iter1个混沌变量,种群多样性得到增强。式(26)中,yiter1为第iter1次参数值;μ为状态控制参数,当μ接近3.6时,映射逐渐进入混沌状态,当μ=4时映射处于完全混沌状态。

根据逻辑优化布谷鸟搜索(logistic-optimized cuckoo search, LOCS)算法原理,确立了机动化箔条幕布放方案优化求解流程,具体求解步骤如下。

步骤 1参数初始化,根据对抗场景,设置场景参数,初始化混沌映射迭代次数iter1、算法维数D、种群规模m、最大发现概率值pa、步长因子η、算法迭代次数iter2等参数。

步骤 2鸟巢位置初始化,随机生成m个布谷鸟巢位置,并根据式(24)进行混沌映射;利用式(18)求取适应度值,选取适应度值最优的m个位置作为初始鸟巢种群。

步骤 3搜索,基于式(23)生成新位置,计算适应度值,并选出最优鸟巢位置。

步骤 4选择,按发现概率pa淘汰较差位置,采用相同数量新位置替换,重新计算适应度值,选出最优位置。

步骤 5判断,判断是否达到最大迭代次数,若达到,终止计算,否则返回步骤2进行迭代更新。

3.4 补弹策略

设每发箔条弹形成有效箔条云后的作用时间为te,若tb-tij>te时,则箔条弹Cij需要进行补发。考虑到箔条弹施放时间及形成有效箔条云所需时间,设置每次补发需要在对应箔条云失效前Δt时刻进行,由此进一步计算出补弹次数、每次补弹时刻及补弹位置,具体如下所示。

(27)

(28)

(29)

(30)

(31)

4 仿真实验分析与验证

4.1 仿真案例

案例 1侦察预警系统发现有主动雷达制导飞行器袭击舰艇,随即开展自卫式机动化箔条幕布放。已知:初始时刻雷达导引头与舰艇位置坐标分别为[0 km,10 km]和[15 km,0 km];飞行速度为150 m/s,初始视线角为0°,初始导弹速度向量角为0°,最大杀伤半径为100 m,雷达导引头工作频率为3 GHz,角分辨力为0.1 rad;舰艇最大行驶速度为20节(10 m/s),初始行驶方向为20°,舰艇最大箔条弹可发射距离为2 km;无人机最大飞行速度为50 m/s,一次最大飞行距离10 km;无人机与舰艇装载箔条弹总量均为30颗,每颗箔条弹箔条数量为5×106根,相邻两枚箔条弹间距离L1为1.8R,单枚箔条弹云团最大可持续时间为60 s,每次补弹需提前3 s进行;海风4级(7 m/s),风向为330°;λ1、λ2、λ3、λ4分别为0.3、0.3、0.2和0.2。

案例 2在常规箔条幕布放过程中,风速与风向是影响干扰效果的重要因素,为此基于案例一重点对风速风向影响情况进行分析。具体参数设置情况如下:风速变化范围和单位增量分别为0～15 m/s和1 m/s,风向变化范围和单位增量分别为0°～360°和10°;其他条件均与案例一保持一致。

仿真实验均在Inter(R) Core(TM) i7-1195G7 CPU@2.90 GHz、16GBRAM、Ubuntu 22.04系统环境中运行。

4.2 仿真结果与分析

4.2.1 方法有效性验证

基于上述构建的机动化箔条幕布放模型,采用蚁群算法(ant colony algorithm, ACA)、蜂群算法(bee colony algorithm, BCA)、CSA和LOCS算法对案例一进行仿真分析[30-31],并与文献[12]提出的常规箔条幕布设结果进行对比分析,以验证机动化箔条幕布放模型有效性。具体参数设置如下:D=5,初始种群个数m为50,Logistic混沌机制迭代次数iter1为50,算法迭代次数iter2为100,对每种算法模式下该案例进行30次仿真计算。

(1) 优化效果对比分析

选取历次仿真优化参数,并求取平均值,得到图4中4种算法迭代曲线对比图和图5迭代运行时间图。由图4可知,在迭代初期LOCS算法适应度值大于其他3种算法,分析认为此现象是由于Logistic混沌序列的遍历性导致的,但在迭代后期,LOCS算法寻优速度明显大于其他算法,迭代16次后即基本寻得较优结果,同时LOCS算法所求最佳适应度值明显小于其他算法,由此证明LOCS算法寻优能力更强。由图5可知,采用ACA、BCA、CSA和LOCS算法寻优所需平均时间分别为1.085 s、1.111 s、1.091 s、1.119 s,LOCS算法虽然增加了混沌映射过程,但计算时间仅较其他算法慢[0.008,0.034]s;对比布放实际需求可得,LOCS算法无论是所需寻优时间还是与其他算法寻优时间差均在可接受范围内,且采用高性能计算机可进一步将时间差距缩小。综上所述,采用LOCS算法对机动化箔条幕进行仿真分析是一种较优的求解方法。

图4 算法迭代曲线Fig.4 Algorithm iteration curve

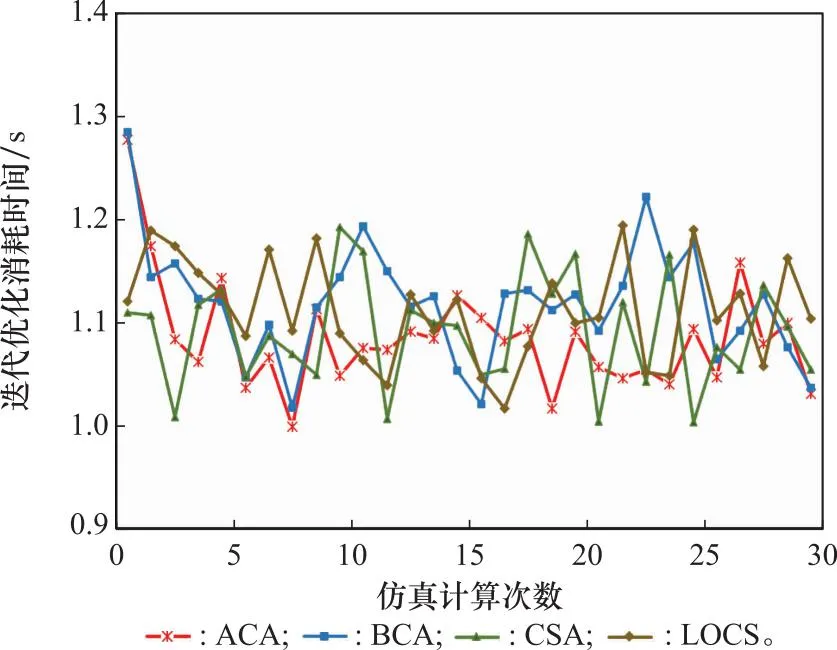
图5 迭代运行时间Fig.5 Iteration run time

(2) 布放效果分析

图6为遮蔽有效性参数z1、z2变化情况;图7为采用机动化布放模型求取的布放结果;表2为图7对应的布放参数初始布放距离为69.82 m;图8为常规箔条幕布放结果;表3为图8对应的布放参数。由图6和图7可知,案例1对抗场景下,遮蔽有效性参数z1和z2始终满足小于0要求,计算结果表明,z3～z6参数值分别为-0.002 rad、1.04 km、-1、-8.78 km,满足约束条件,由此证明干扰效果全程有效。机动化箔条幕构设共需消耗6颗箔条弹,整个过程无需补弹,对抗过程持续50.13 s时,舰船驶出雷达导引头跟踪波束范围,箔条幕轴向较初始时刻弹目垂线偏转角度为-5.31°,舰船机动偏转角度为29.43°,初始时刻舰船和无人机分别布放箔条弹2发和4发,布放方向φ1和φ2分别为29.64°和75.66°。对比图7和图8布放结果可知,相较于机动化箔条幕布放方法,常规箔条幕布放需消耗箔条弹9枚,初始布放8枚,补弹1枚,整个对抗过程持续59.37 s。综上所述,本研究提出的布放方法较大程度提升了舰船自卫效果,且有效节约了作战资源。

图6 遮蔽有效性参数变化曲线Fig.6 Shading effectiveness parameter variation curve

图7 案例1机动化箔条幕布放结果Fig.7 Motorized chaff screen arrangement results of case 1

表2 案例1机动化箔条幕布放参数Table 2 Motorized chaff screen arrangement parameters of case 1

图8 案例1常规箔条幕布放结果Fig.8 Traditional chaff screen arrangement results of case 1

表3 案例1常规箔条幕布放参数Table 3 Traditional chaff screen arrangement parameters of case 1

4.2.2 风速风向影响分析

图9和图10为案例2仿真结果。其中,图9表示目标函数值结果,图10表示箔条弹消耗量结果。由仿真结果可知,在案例2对抗场景下,风速为0～15 m/s、风向为0°～360°范围内,均可求取有效的机动化箔条幕布放结果,目标函数值介于0.06～0.13,且箔条弹消耗数量分布于6～7发。由此可见,与常规箔条幕布放容易受风速风向影响相比[14],机动化箔条幕布放模型在初期构建时,充分考虑了风速风向因素,有效提高了箔条幕环境适应性。

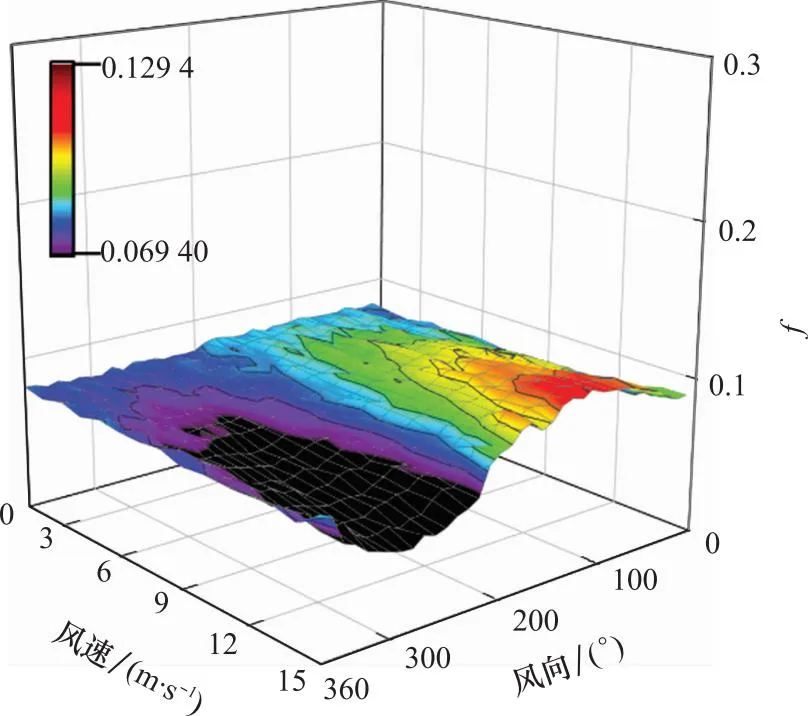
图9 不同风速风向条件下目标函数值Fig.9 Target function value under different wind speed and direction

图10 不同风速风向条件下箔条弹消耗量Fig.10 Chaff consumption under different wind speed and direction

5 结 论

针对雷达导引头新型抗干扰技术导致传统箔条干扰方法干扰效能降低问题,提出了一种机动化箔条幕构设方法,通过无人机和舰船对箔条弹协同布放完成箔条幕构设,使箔条幕质心随时间有效移动,并保证舰船成功逃逸。基于机动化干扰原理,构建了箔条幕布放模型,确立了基于改进的布谷鸟搜索算法进行布放方案求解的总体思路,进而构建了布放效能条件,采用Logistic混沌机制改进了布谷鸟搜索算法,并建立了补弹策略。仿真实验分析表明,本文提出的机动化箔条幕干扰方法能够保证舰船在有效作用时间内成功逃出雷达导引头跟踪范围,同时与常规箔条幕干扰方法相比,机动化箔条幕干扰方法能够有效减少舰船逃逸时间、降低箔条弹消耗量,同时求取的布放方案抗风向风速变化更强。