基于重传错误率估计的自适应HARQ

付 钰, 刘奕彤, 杨鸿文

(北京邮电大学大学信息与通信工程学院, 北京 100876)

0 引 言

混合自动重传请求(hybrid automatic repeat request,HARQ)是一种结合前向纠错(forward error correction,FEC)与自动重传请求的技术,能够保障数据传输的可靠性,在现代通信系统中发挥着关键作用[1]。在HARQ机制下,虽然单次接收到的错误数据包不能独立地正确译码,但其包含有一定的有用信息,因此接收端通常将错误的数据存储,并与重传得到的数据进行合并后再译码[2]。这一存储及合并的机制使系统对衰落更具鲁棒性,且有效提高了系统的吞吐率[3]。

在无线系统中,由于路径损耗、衰落等原因,每次传输时的链路质量会有不同。因此,HARQ系统的每次传输可以选择不同的调制与编码方案(modulation and coding scheme,MCS)以及发送功率,以适配当前传输时的信道质量[4-5]。一方面,选择稳健的MCS等级和较大的发送功率可以提供高可靠性;另一方面,选择尽可能高的MCS等级和较小的发送功率可以减少信道资源和能量的消耗[6]。对MCS和发送功率的选择都会影响到HARQ系统的吞吐率及能耗性能。值得注意的是,吞吐率与能耗性能均与重传合并后的译码错误率有关,这一错误率也受到MCS与功率选择的影响。然而,在重传采用不同MCS的情况下,HARQ合并后的错误率没有闭式解,使得HARQ的优化问题存在困难。

现有的实际系统如长期演进(long term evolution,LTE)和5G系统支持自适应HARQ和非自适应HARQ[7],其中自适应HARQ每次传输时选择MCS的方法为与信道质量指示符(channel quality indicator,CQI)进行映射,使当前单次传输的误码率小于某个固定值(通常为10%)[8-9],非自适应HARQ重传时不改变MCS。基于现有系统的自适应HARQ方案,文献[10-12]通过优化对信道质量的估计和预测以优化链路自适应,文献[13-15]通过优化每次传输的目标错误率以优化链路自适应,文献[16]使用机器学习的方法优化MCS的选择,从而提升系统的吞吐率等性能,但以上优化方法的自适应MCS仍是以单次传输的错误率或吞吐率为选择指标,没有考虑HARQ合并后译码性能的提升,因此还有很大的优化空间。

已有一些文献研究了考虑HARQ合并的优化问题,此时合并后的错误率计算问题是主要难题。文献[17-18]通过对仿真得到的错误率曲线进行拟合,提出了HARQ合并后的错误率近似公式并用于HARQ的优化。文献[19]利用拟合得到的合并后中高信噪比(signal to noise ratio,SNR)下的错误率上界进行HARQ的优化。文献[20-21]借助了一种近似错误率计算方法。然而,以上错误率计算方法均只适用于重传不改变MCS的情况,不能解决不同MCS的传输合并后的错误率计算问题,因此只能用于非自适应HARQ的优化。现有的大量研究通过计算累积互信息来判断HARQ合并后的译码性能,如文献[22-28]借助累积互信息的方法,对不同的场景和模型从吞吐率、能量效率等角度研究了HARQ每次传输时功率及码字长度的自适应选择。这一方法适用于不同MCS的传输的合并,即适用于自适应HARQ的优化研究,然而通过互信息进行判断隐含了编码能达到香农极限的假设,实际编码在高阶调制下与香农极限还有较大的差距。

解决自适应HARQ优化问题的关键是计算每次重传合并后的译码错误率,因此本文借助判决域半径方法[29]对每次传输进行等效,给出了HARQ合并后估算码字错误率的近似公式,可以解决采用不同MCS传输合并后的错误率计算问题。基于这一错误率估算公式,本文提出了不同的自适应HARQ的优化策略,分析了吞吐率和能耗的权衡关系并给出了能够兼顾吞吐率和能耗性能的优化策略。

本文内容安排如下:第1节给出了HARQ系统每次传输及合并的系统模型,以及优化指标吞吐率和能耗的定义;第2节引入了基于判决域半径的错误率估算方法,并借助此方法实现了HARQ合并后的译码性能估计;第3节分别从吞吐率和能耗的角度对自适应MCS和自适应功率的方法进行了分析,并提出了不同的自适应优化策略;第4节给出了仿真结果和分析;第5节对文章进行了总结。

1 系统模型

考虑如图1所示的系统。本研究主要考虑HARQ过程,其底层可以是任意的物理波形设计,例如可以包括多输入多输出(multiple input multiple output, MIMO)、正交频分复用(orthogonal frequency division multiplexing, OFDM)、正交时频空(orthogonal time frequency space, OTFS)、非正交多址接入(non-orthgonal multiple access, NOMA)等。从HARQ的角度来说,长度为K的信息比特经FEC编码成为二进制码字,码字经调制成为发送符号向量x,其元素为M进制正交幅度调制(M-quadrature amplitude modulation,M-QAM)符号。x可能通过MIMO、OFDM等方式传输,接收端检测后形成接收信号向量y。各种底层技术可以抽象到从x到y的信道模型中。

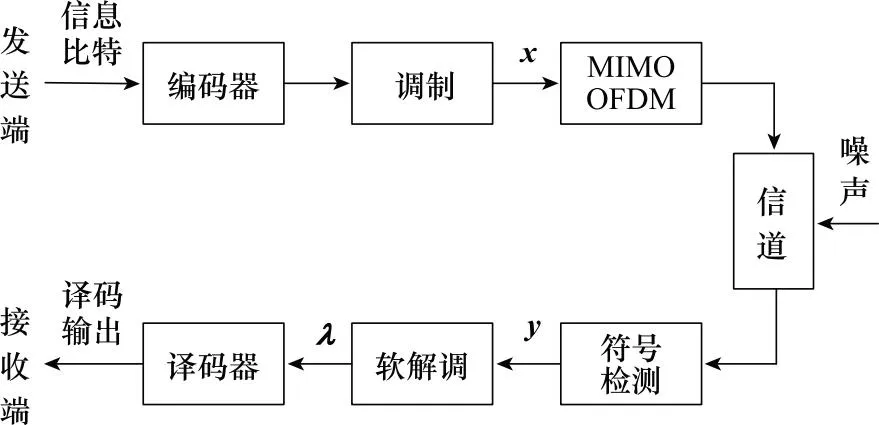
图1 数据传输系统流程图Fig.1 Data transmission system flow chart

在HARQ中,相同的信息可能需要多次传输。在第k次传输中,发送信号向量xk与接收信号向量yk的关系可以建模为

(1)

式中:xk的每个元素都是单位能量星座中的星座点;pk是发送功率;gk是平均信道增益;diag(ak)是以ak为对角线元素的对角矩阵,ak是功率归一化的幅度增益向量,表示xk中每个符号的幅度增益;zk是方差为N0的零均值复高斯噪声;kmax是最大传输次数。当次传输的信噪比(signal to noise ratio,SNR)为γk=pkgk/N0。

(2)

接收端对接收信号进行软解调,得到对应的比特级对数似然比(log likelihood ratio, LLR)向量λk,与前k-1次传输合并后输入译码器进行译码。每次传输后,如果译码正确,接收端反馈确认字符(acknowledge character, ACK)信号;如果译码错误,接收端存储软信息λk并反馈否定应答(negative acknowledgement, NAK)信号请求重传,直到发送端收到ACK信号,或直到达到最大传输次数,传输结束。

在每次重传后,接收端先合并再译码,如图2所示。

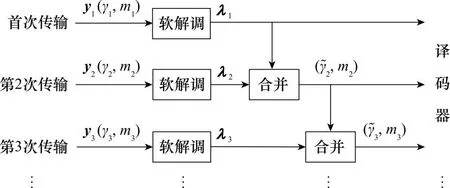
图2 HARQ重传合并示意图Fig.2 Illustration of HARQ retransmission and combining

以前两次传输为例,如果重传不改变MCS,即x2=x1,则最优的合并方式是最大比合并(maximal ratio combining,MRC)[23],合并后的等效SNR为

(3)

而对于优化的HARQ来说,重传时非常有可能选择不同的MCS,此时x2与x1不同,HARQ合并的方式是软信息合并。软合并后的信道质量不等于SNR相加,导致合并后译码性能估计问题难以解决。

HARQ系统的性能主要包括吞吐率和能耗。吞吐率定义为成功传输的信息比特数与发送符号数之比[23],即

(4)

式中:Pe为传输结束后码字的残余错误率;nmk表示第k次传输采用MCS等级为mk的发送符号数,即xk的向量长度。如果第k′次传输后译码成功,则有nmk=0,k>k′。

本文中的传输能耗指成功接收每个信息比特所需的平均发送能量,即

(5)

式中:p0表示系统中的电路损耗等其他能耗,通常影响较小,简单起见不妨假设p0=0。β-1即为能量效率。

根据式(4)和式(5),吞吐率和能耗均是HARQ过程中MCS等级{mk}和功率{pk}的函数。HARQ系统的优化意在通过优化{mk}和{pk}达到尽可能高的吞吐率和尽可能低的能耗。需要注意的是,式(4)和式(5)中的残余错误率Pe是所有{mk}和{pk}的函数,同时也是所有信道质量{gk}的函数。优化问题存在的困难在于,一是Pe与{mk}、{pk}和{gk}的函数关系没有闭式解,二是不能提前预知{gk}。在第k次传输时,未来的信道{gk+1,gk+2,…,gkmax}是未知的,因此只能在每次传输时即时优化。与此同时,在第k次传输时,已经完成的传输不能改变,即第k次传输时不能改变{m1,m2,…,mk-1}和{p1,p2,…,pk-1}。以下先解决错误率估计问题,然后给出每次重传的优化策略。

2 重传合并后的译码性能估计

2.1 基于判决域半径的近似方法

码字的判决域是决定译码错误率的关键因素,已有研究表明通过判决域平方半径的分布可以估算信道编码的码字错误率[29]。同时,由于判决域在几何结构上基本与SNR无关,故使用基于判决域半径的错误率估算方法,在固定的MCS下,即可基于同一组半径样本估计任意SNR下的错误率。基于该方法,SNR为γ、MCS等级为m时单次传输的码字错误率[32]近似为

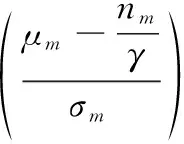
(6)

式中:μm,σm分别是码字判决域平方半径的均值、标准差,与码字采用的具体MCS有关,可通过仿真测量获得;nm是码字对应的发送符号向量x的向量长度;Q(·)为高斯Q函数。式(6)给出的近似估算比实际偏低,与蒙特卡罗仿真结果相差约为0.2 dB。对此可以有更准确的估算公式[32],但式(6)形式更简单,有利于后续的等效计算。

2.2 HARQ合并后的错误率估计

(7)

(8)

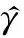
(9)

可以注意到,如果两次发送的MCS原本就相同,式(9)将退化为式(3)。

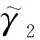
(10)

(11)

3 基于错误率估计的自适应优化

由于实际系统不能预知未来的信道质量,每次传输时也不能改变过去,因此需在每一次传输时,根据当前已知的信息{g1,g2,…,gk}、{m1,m2,…,mk-1}和{p1,p2,…,pk-1}来优化mk及pk。

根据等效估计模型,触发第k次传输后,式(4)的系统的吞吐率和式(5)的能耗可以分别具体表示为

(12)

(13)

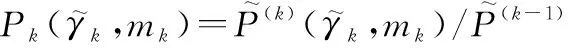
针对吞吐率ηk(pk,mk)和能耗βk(pk,mk)这两个优化目标,首先提出以下优化策略。

策略1通过优化mk及pk使得吞吐率ηk(pk,mk)最大。

由式(12)可得到如下定理。

定理 1对任意k≥1和给定的mk,k次传输后的系统吞吐率ηk(pk,mk)是发送功率pk的单调增函数。

证毕

由定理1可知,为达到最大吞吐率,只需在最大发送功率下选择最优的MCS,即

(14)

式中:pmax是功率约束下的最大发送功率;M是可选择的MCS等级的集合。

策略2通过优化mk及pk使得能耗βk(pk,mk)最小。

在一定功率约束下,最小化能耗的优化方法为

(15)

对最小化能耗的优化结果也有明显的规律,即普遍选择最低的MCS等级,从而能够大幅降低发送功率。

策略1和策略2的优化结果体现出两个优化目标存在的权衡关系,即为使吞吐率最大,需选择最大的发送功率,但会因此导致能耗较大;为使能耗最小,会选择最低的MCS等级,但会导致发送符号数量大,吞吐率显著降低。同时考虑两个优化目标,进一步提出以下优化策略。

策略3以吞吐率为第一优先级,能耗为第二优先级进行优化。

根据式(12)及策略1的优化结果,MCS的选择是吞吐率的主要影响因素,因此优先考虑吞吐率性能,即首先选择能使吞吐率达到最高的MCS,再在合理范围内选择发送功率以优化能耗性能,具体步骤如下。

步骤 1每次传输时,在pk=pmax条件下,根据式(14)选择使吞吐率最大的MCS;

步骤 2采用所选择的MCS,根据最小化能耗优化发送功率,即

(16)

策略4以能耗为第一优先级,吞吐率为第二优先级进行优化。

与策略3相对应,首先选择使能耗最小的发送功率,再选择MCS等级以提升吞吐率,具体步骤如下。

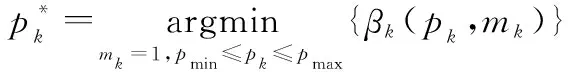
步骤 2采用所选择的发送功率,根据最大化吞吐率优化MCS,即

(17)

对于策略4,由于MCS等级的颗粒度较大,给定发送功率后,如果提升MCS会使错误率发生明显变化,因此步骤2的优化结果通常是保持最低的MCS等级,只有当信道质量足够好时才会选择更高的MCS等级,这与策略2的优化结果一致。因此,策略4与策略2是近似等价的。

4 仿真结果

4.1 仿真配置

在仿真中,使用5G标准中的准循环低密度奇偶校验码(quasi-low-density parity-check codes,QC-LDPC)码作为二进制FEC编码。信息比特数K=1 056 bit,母码码率为1/3,通过速率匹配可以适配不同的目标码率。码字经M进制调制后通过信道进行传输。仿真中可供选择的MCS选取自5G标准[9],具体如表1所示。

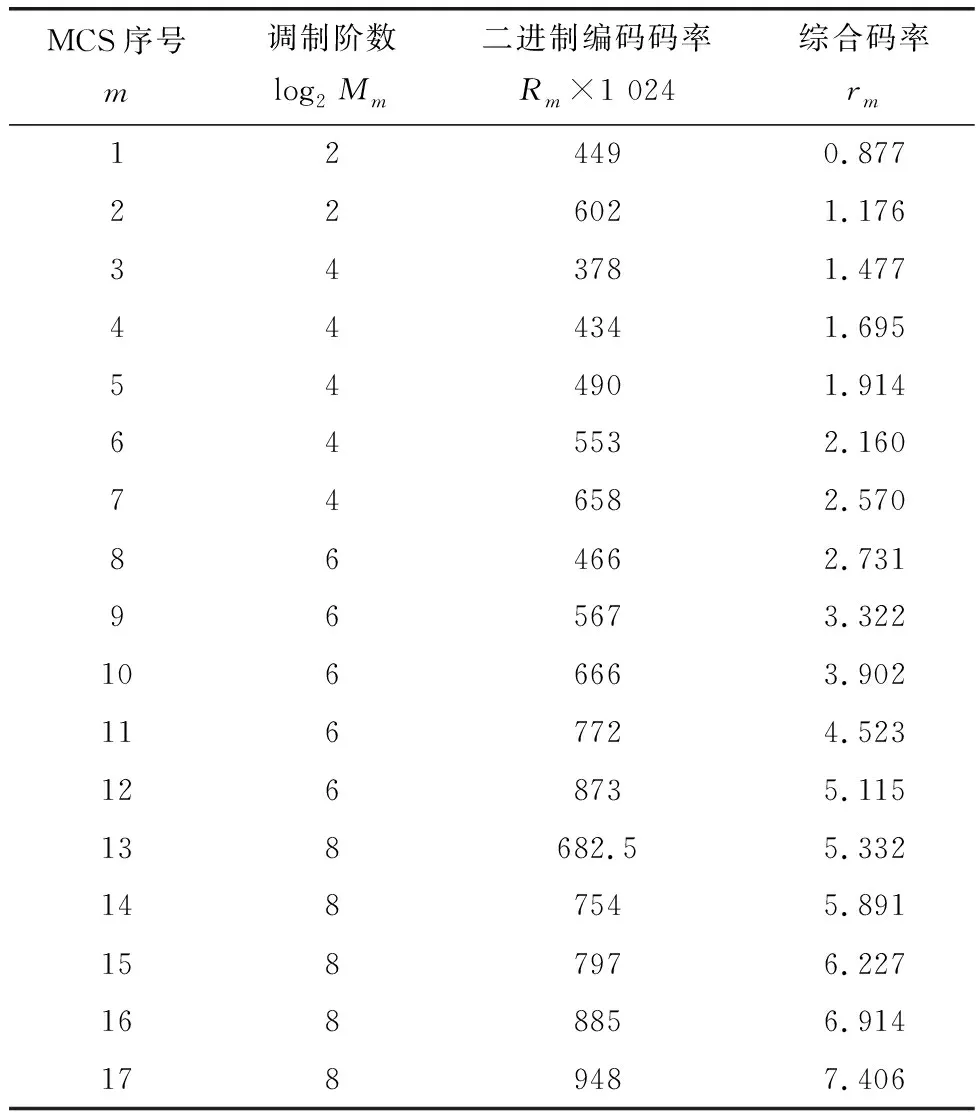
表1 MCS索引表[9, Table 5.1.3.1-2]Table 1 MCS index table [9, Table 5.1.3.1-2]

不同MCS等级m具体体现为不同的调制阶数log2Mm及不同的二进制编码码率Rm,综合码率记为rm=Rmlog2Mm。通过仿真得到码字在不同MCS下的判决域半径信息。

在仿真中,假设发送端、接收端均确知当前的信道状态信息,且发送端存储码字每次传输时的SNR及MCS信息。

4.2 等效估计方法的验证

考虑HARQ传输两次的情况,所提等效估计方法的结果与仿真结果的对比如表2所示。

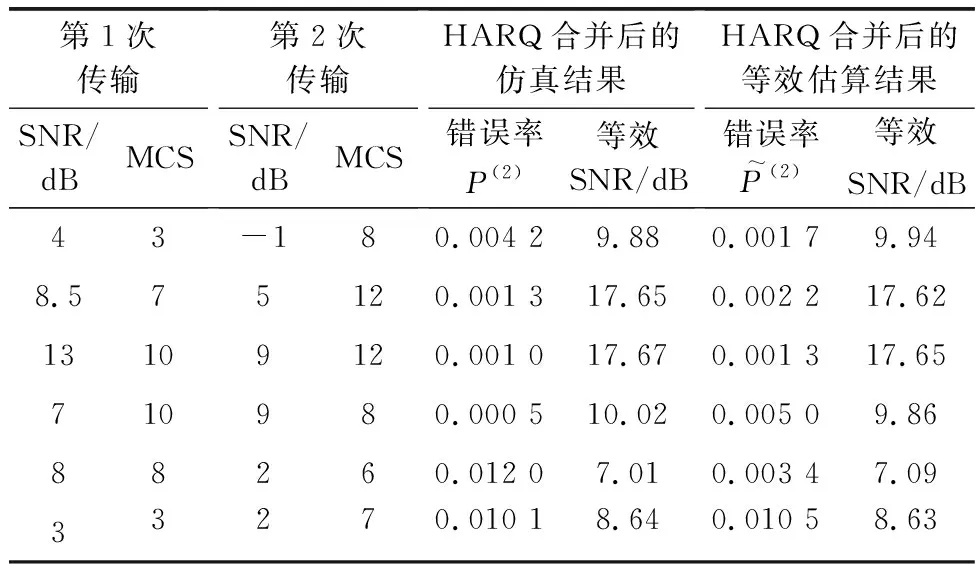
表2 等效估计方法与仿真结果对比Table 2 Comparison of equivalent estimation methodand simulation results

表2对比了给定的几组传输条件下,等效估算结果与蒙特卡罗仿真结果的HARQ合并后的码字错误率和等效信道质量。其中,仿真结果的等效信道质量由码字错误率用式(6)按第2次传输的MCS映射到SNR得到。

从表2的结果可以看出,估算的等效SNR与仿真结果的误差小于0.2 dB,验证了所提等效近似方法的可靠性。对传输3次及以上的估算结果类似,此估算误差对后续的优化影响很小。

4.3 自适应优化结果及分析

图3和图4分别给出了瑞利块衰落信道下不同传输方案的吞吐率及能耗性能的仿真结果。其中,信道平均增益归一化(E[gk]=1),每个码字的最大传输次数为4次(kmax=4),包含首次传输和最多3次重传。仿真中的对比方案包括传统自适应MCS方法和非自适应方法。传统自适应MCS 方法在每次传输时根据当前信道质量选择使单次传输错误率小于某个固定值Pc的最高MCS等级,即

(18)

通常取Pc=10-1。非自适应方法则是首次传输时根据式(18)选择MCS,重传时MCS不变。以上两种方法中,发送功率均固定为pk=1。策略1～策略4分别根据第3节中所述方法选择MCS及发送功率,其中发送功率的约束为0.01≤pk≤1。系统吞吐率性能的仿真结果如图3(a)所示。由于每次传输时,功率pk是变量,故此图中横坐标为归一化的导频SNR。对照方案(非自适应、传统自适应MCS)的发送功率为1。所提方案中,策略1对应的发送功率为1,策略2～策略4的发送功率由优化结果确定,图中纵坐标为式(4)定义的系统吞吐率。从图3(a)中可以看出,在相同的信道质量下,策略1的吞吐率最高,比非自适应方法提高了7%～20%,比传统自适应MCS方法提高了2%～7%。该方法的吞吐率增益来源于在合理的范围内选择了更高的MCS等级进行传输。以导频SNR为10 dB时为例,不同方案下MCS选择的差别如图3(b)所示。可以看出策略1比非自适应和传统自适应MCS方法更多的选择了高等级的MCS,从而获得了吞吐率的增益。

图3 不同传输方法的吞吐率性能Fig.3 Throughput performance of different transmission methods

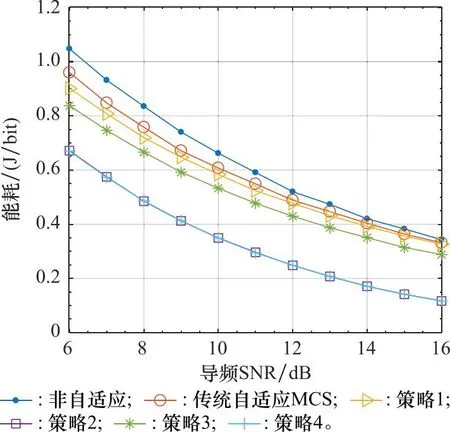
图4 不同传输方法的能耗Fig.4 Energy consumption of different transmission methods

在图3(a)中,策略3比策略1的吞吐率性能有所下降,这是因为策略3相比策略1减小了发送功率。考虑发送功率的因素,按实际发送功率将导频SNR折算为实际传输的比特SNR,可以得到图3(c)所示的吞吐率性能。由图3(c)可以观察到,对于相同的SNR,策略3保持了吞吐率性能的优势,比非自适应方法和传统自适应MCS方法在吞吐率性能上分别提高了20%～40%和10%～20%,SNR增益分别约为1 dB和0.5 dB。一方面策略3与策略1一样选择了更高等级的MCS,另一方面策略3以微小的吞吐率损失节约了较大的发送功率,因此策略3在实际SNR下表现出更好的性能优势。

此外,图3(a)和图3(c)也体现出了策略2和策略4的等价性,二者因为选择低MCS等级,所以在吞吐率性能上表现出明显的缺陷。

图4给出了不同传输方法的能耗的仿真结果,横坐标为导频SNR,与图3(a)对应;纵坐标为式(5)定义的能耗。图4体现了策略2和策略4在能耗上的显著优势,但因其在吞吐率性能上的缺陷,在实际应用中明显受限。相比之下,策略1和策略3在具有高吞吐率的同时,在能耗性能上也有一定增益,其中策略1的增益来源于高等级的MCS对应的发送符号数更少,而策略3进一步降低了发送符号功率,因此能耗更低。图4表明,策略3的能耗比非自适应方法与策略1分别降低了20%与10%。

5 结 论

自适应HARQ系统可以通过优化MCS和发送功率来实现更高的吞吐率和更低的能耗,这与HARQ合并后的译码性能研究具有重要关系。本文借助判决域半径方法,解决了重传采用不同MCS合并后的译码性能估计问题,可以比较准确地估算软合并后的等效信道质量。基于此估算方法,本文分析了最大化吞吐率和最小化能耗的权衡关系,提出了不同的自适应HARQ的优化策略,其中一种优化策略能够更好地兼顾吞吐率与能耗性能。仿真结果表明,该方案在吞吐率与能耗性能上均比传统HARQ方法具有一定增益。