挖掘机铲斗土方动力学参数辨识方法研究*

吕 磊,闫家铭,徐玉兵,宋士超

(徐州徐工挖掘机械有限公司,江苏 徐州 221121)

0 引言

挖掘机是工程机械的主力机种,每年都要消耗巨量的燃油。对我国而言,降低挖掘机能耗具有经济、环境和能源安全方面的重要意义。挖掘机降耗节能方面的一项主要挑战来自于其工况和负载多变,挖掘机工作模式设定无法很好地适应这种多变的负载,发动机、液压泵和负载之间不能很好地匹配,导致能量浪费。本研究的目的是对挖掘机工作过程中负载进行辨识,为发动机-液压泵-负载匹配控制策略提供准确的输入,帮助实现三者之间良好的匹配,达到节能增效的目的。

在工程机械领域,国外许多公司,如卡特、约翰迪尔等,都开展了动态称重技术的研究,但相关技术主要应用于装载机[1-2]。液压挖掘机载荷辨识研究开始得相对要稍晚一些,直到2017年卡特彼勒公司才推出了两款带有称重系统的挖掘机,分别为 F320 和 F323 型挖掘机。在国内,这一课题研究在近些年才得到重视,陆续有多篇文章或学位论文以此为研究课题得以发表[3-5]。

对挖掘机负载进行辨识的方法中,一条比较直观的途径是通过测量液压泵的出口压力来对载荷进行估计。一般而言,负载越大对应的泵出口处压力越大,所以泵出口压力可以反映负载的一些信息。但泵出口压力与挖机铲斗中的土方量并不是直接对应关系,还与工作装置的构型和运动相关,因而单独通过泵出口压力不能准确地辨识出铲斗内土方量。也有一些学者尝试基于视觉方式对铲斗内土石方进行测量,这种方式要求在铲斗四周布置相机,否则易被遮挡。即便如此,相机还是很难对土方内的状况进行判断,如土方的密度和压实程度等,因而难以比较精确地辨识出土方量。

另一项技术路线基于力学分析,又分为静力学分析和动力学分析。由于大多数挖掘机铲斗既通过轴又通过多连杆与斗杆相连,在不增加其他假设条件的基础上单纯基于静力学分析无法得到确切解。目前,动力学分析法是研究人员更为认可的求解途径。

1 应用说明和假设

本文所采用的辨识方法是基于挖掘机工作装置动力学建模,通过安装在挖机上一系列传感器获取必要的信息,以期对挖机每次挖取的土石方进行自动辨识。传感器主要包括安装在挖掘机工作装置三个转轴上的关节编码器以及三个液压油缸两端的压力传感器。关节编码器用于测量工作装置的构型以及运动速度。在实际应用中,也可以通过测量液压缸的长度来获取工作装置的构型及运动速度,不过从应用便捷性及测量精度的角度看,通过光电编码器测量角度/角加速度应是更优选择。

辨识针对的场景是:挖掘机铲斗挖取一定量的土石方后,铲斗与外界脱离接触(铲斗内的土方量不再变化,相对于铲斗也不做运动,即铲斗与土方“融为”一体),其后挖掘机的工作装置移动土方。各传感器测量搬运过程中的角度和压力信息,并将一定量的测量数据传送到挖掘机的计算单元,软件基于测量信息计算铲斗及土石方合体的质量、质心位置和转动惯量。铲斗自身的质量、质心位置和转动惯量都是定值,据此可以获得土石方的相关参数。

测量过程中,挖掘机的回转动作理论上不会对辨识产生影响,因而可以不予考虑。在实际应用过程中,如果工作装置的运动引起挖掘机整体的运动或振动,这将影响辨识结果的准确度,需避免。

2 挖掘机工作装置动力学建模

2.1 建模说明

2.1.1 各位置点和参数说明

图1为单斗液压挖掘机的侧平面图。由于转台的运动对辨识无影响,所以运动学和动力学分析都可以在纸面所处的平面内进行。图中相关点和参数的定义见表1。

图1 液压挖掘机工作装置几何构型示意图

表1 挖掘机结构点和参数定义表

由于动力学分析限定在平面内,所以I1、I2和I3定义为绕穿过G1、G2和G3垂直于纸面的轴的转动惯量;上述参数中,待辨识的参数为m3、I3、r3和θ6,由于每次铲运过程中土方量不再变化且与铲斗间无相对运动,因而在一次铲运过程中可认为都是定值。

2.1.2 坐标系定义

为建模方便,共定义了四个坐标系,分别以O、Ⅰ、Ⅱ、Ⅲ来命名。

O坐标系:固定的全局坐标系,坐标系原点定义在动臂与车体的铰结处,X坐标轴垂直于执行机构所在的平面(纸面),Y坐标轴水平向右,Z坐标轴垂直向上。

Ⅰ坐标系:附着于动臂上的坐标系,随动臂的转动而转动。坐标系原点O1与全局坐标系原点O相同,X1与X轴平行,Y1轴自O1指向动臂与斗杆的铰接处O2,Z1轴由右手法则确定。

Ⅱ坐标系:附着于斗杆上的坐标系,随斗杆的转动而转动。坐标系原点位于斗杆与动臂的铰接点O2,X2与X轴平行,Y2轴自O2指向斗杆与铲斗的铰接处O3,Z2轴由右手法则确定。

Ⅲ坐标系:附着于铲斗上的坐标系,随铲斗的转动而转动。坐标系原点位于斗杆与铲斗的铰接点O3,X3与X轴平行,Y3轴自O3指向铲斗的斗齿尖N处,Z3轴由右手法则确定。

2.1.3 标记、符号说明

为坐标系Ⅲ到坐标系Ⅱ的转换矩阵(不考虑平移)。

其中,c1=cos(θ1)、c2=cos(θ2)、c3=cos(θ3);s1=sin(θ1)、s2=sin(θ2)、s3=sin(θ3)。特别说明,为简化公式书写,c12=cos(θ1+θ2),s12=sin(θ1+θ2),在后续公式推导过程中一些表达项可以此类推。此外,一个符号变量左上角的标号(O,Ⅰ,Ⅱ,Ⅲ)代表的是该变量在相应坐标系的表达。

2.1.4 建模的假设条件

在本文的分析中,没有考虑油缸长度变化及连杆构型变化引起的质心位置和转动惯量的变化。

动力学分析中,各转轴处的摩擦没有考虑在内。

假设动臂、斗杆和铲斗完全刚性,即三者没有弹性形变。

2.2 系统动力学方程的构建

挖掘机的工作装置可以看作为一个三自由度(不考虑转台转动)的串联多体结构。对于这类多体动力学建模,最为常见便捷的方法是拉格朗日方程法:

(1)

L=K-P

(2)

公式(2)中,K为工作装置的总动能,P为工作装置的总势能(以Y轴为零势能水平基准),即

K=K1+K2+K3

P=P1+P2+P3

(3)

其中,K1为动臂动能,K2为斗杆动能,K3为铲斗与土石集合体的动能;P1为动臂势能,P2为斗杆势能,P3为铲斗与土石集合体的势能。

动臂动能:

(4)

(5)

将式(5)带入式(4),可得动臂动能:

(6)

动臂重力势能:

P1=m1g*r1*s14

(7)

其中,g为重力加速度。

斗杆动能:

(8)

其中,

(9)

将式(9)带入式(8)可得

(10)

斗杆重力势能:

P2=m2g(L1s1+r2s125)

(11)

铲斗动能:

(12)

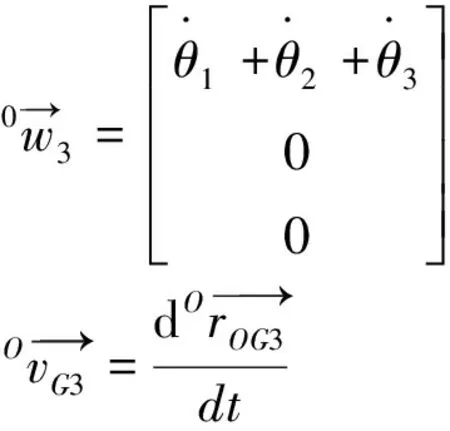
(13)

将式(13)带入式(12),

(14)

铲斗势能:

P3=m3g(L1s1+L2s12+r3s1236)

(15)

将式(6)、(7)、(10)、(11)、(14)、(15)带入式(2)可得:

-m1gr1s14-m2g(L1s1+r2s125)-m3g(L1s1+L2s12+r3s1236)

(16)

挖掘机工作装置共有3个自由度,所以可以构建3个方程。将式(16)带入系统动力学方程式(1)

可得,

m2g(L1c1+r2c125)+m3g(L1c1+L2c12+r3c1236)=τ1

m3gr3c1236=τ3

(17)

式(17)3个方程右侧的τ1、τ2和τ3是3个液压油缸的净力对各自转轴所产生的力矩,逆时针方向为正。

τ1=f1*h1(θ1)

τ2=f2*h2(θ2)

(18)

τ3=f3*h3(θ3)

其中,f1、f2和f3分别为3个液压油缸两端压力相抵消后产生的净力;h1(θ1)、h2(θ2)和h3(θ3)分别为3个净力相对于3个转轴的力臂,由以下三式给出:

h1(θ1)=OA*sin(∠OAB)

(19)

其中,∠AOB=∠AOY+θ1+∠BOO2,∠AOY和∠BOO2都为结构角(固定值),θ1测量获取。

(20)

其中,

∠CO2D=π-θ2-∠DO2O3-∠CO2,∠DO2O3、∠CO2O、CO2、DO2都为结构参数,固定值,θ2由测量获取。

由于连杆机构的存在,h3的计算稍显复杂,计算如下:

h3(θ3)=EO3*sin(∠FEO3)

(21)

其中,

EF2=EH2+FH2-2*EH*FH*cos(∠EHF),

∠EHF=∠EHO3-∠FHO3,

∠HO3M=π-∠HO3O2-∠MO3N-θ3

在上述h3计算过程中,∠HO3O2、∠MO3N、∠EHO3、HO3、MO3、FH、FM、EH、EO3都为机构参数,固定值,θ3为测量值。

式(17)没有整理成常见的多体动力学方程的标准形式,其原因在于所构建的动力学方程是用于参数辨识,而不是通过求解动力学方程来获取系统的动力学演化过程。

2.3 非线性方程组求解法:牛顿迭代法

式(17)是关于待辨识参数m3、r3、θ6和I3的非线性方程组,本文采用牛顿迭代法予以求解。令,

(22)

可以将式(18)带入式(22)中获得完整的表达式。

构建如下雅克比矩阵:

(23)

方程组(18)包含有3个方程,但待辨识参数有4个,所以需通过多次测量以提高辨识结果的准确度。对于多次测量,增加雅克比矩阵的维度即可。需要注意的是,辨识所用数据对应的工作装置构型之间应具有一定的差异,以避免病态矩阵。

牛顿法迭代过程:

第k步,

(24)

F1、F2和F3的下标代表的是测量次序,k代表的是牛顿迭代循环过程中的第k步。整个迭代过程持续进行,直至辨识结果达到一定标准下的收敛。

3 辨识方法的仿真验证

本文在ADAMS中构建了一款液压挖掘机,并驱动工作装置中的3个执行机构,即动臂、斗杆、铲斗,协同动作,完成铲斗的内收、提升和外翻动作。在此过程中,记录下各转轴的角度、角速度、角加速度以及各油缸的净力,并带入辨识方程以计算各待辨识参数。将辨识结果与参数的真实值进行比对以检验所提出辨识方法的效果。

3.1 仿真配置

图2为生成算法验证所需数据所构建的ADAMS模型。表2给出了ADAMS模型仿真中所用参数的取值。

图2 用于生成验证数据的挖掘机ADAMS模型

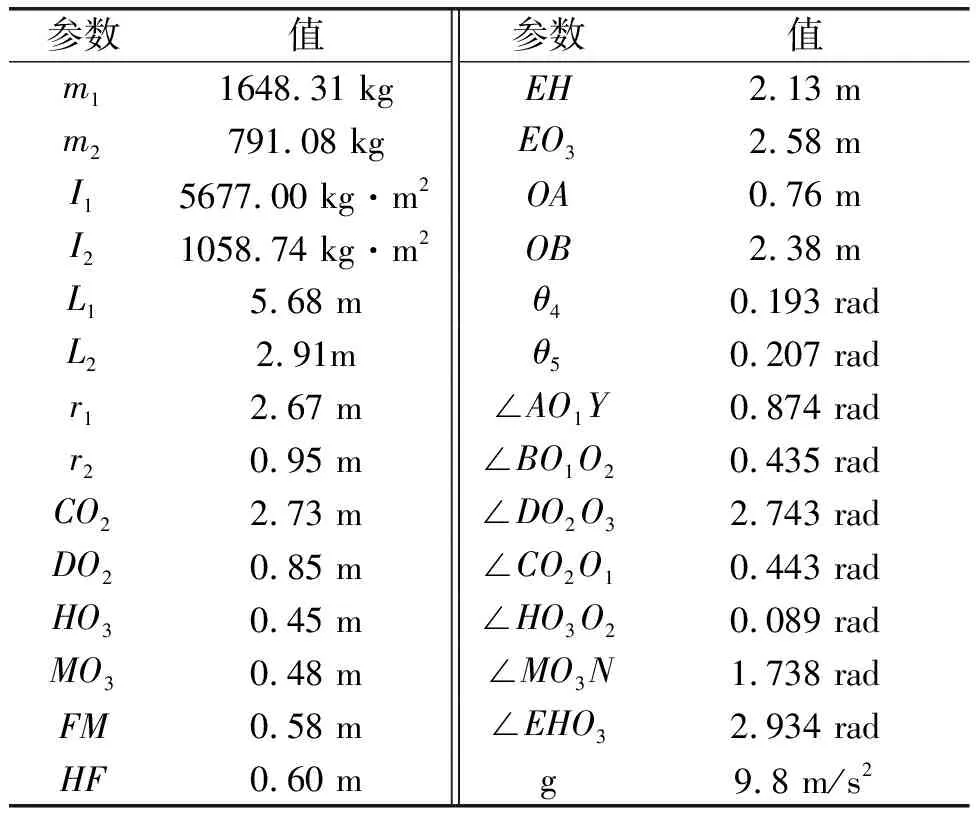
表2 挖机模型的相关参数

图3 动臂、斗杆和铲斗转轴的角度轨迹

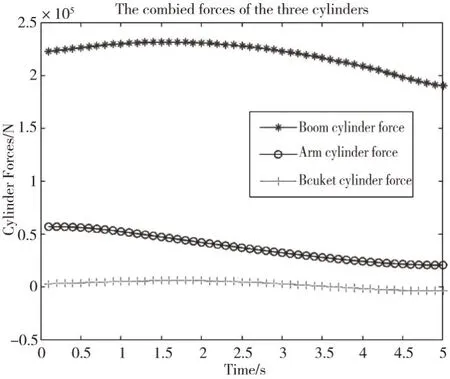
图4 动臂、斗杆和铲斗的液压油缸生成的净力

3.2 辨识结果准确度检验

将ADAMS仿真模型生成的数据带入本文所提出的辨识方法,在同样条件下(即原样不变的情况下运行辨识程序)进行了7次重复辨识,得到的辨识结果如表3所示。

表3 辨识结果

首先可以观察到的是铲斗复合体质量的辨识结果非常稳定,与真实值之间的偏差非常小,可以说质量的辨识结果准确无误。辨识得到的r3(即铲斗转轴到铲斗复合体质心的距离),其绝对值比较稳定且基本等于真实值,但会出现负值;而θ6即铲斗转轴-质心的连线与坐标系III Y轴的夹角(逆时针为正)的辨识结果完全无规律可言。但r3与θ6结合所给出的质心位置却非常接近真实值,如表3中第四、五列所示。需要说明的是,构建动力学方程时,质心位置可用笛卡尔坐标也可以用极坐标来表达。本文用极坐标来表达质心位置主要是为了方程推演的方便。

转动惯量I3的辨识结果波动很大,与真实值相差甚远,可以说没有什么参考价值。原因在于:所构建的动力学方程组只有3个方程,而未知参数有4个。虽然通过多次测量可以生成方程数量远大于4(如本文中500次测量对应1500个方程)的方程组,但为求解该非线性方程组所构建的雅可比矩阵仍然比较接近于病态矩阵;在动力学方程中,每个方程I3仅出现一次,且其系数只有3个转轴的角加速度之和,因而方程的病态性主要体现在I3上,其辨识结果非常易于受影响,波动非常大。

运行辨识程序,进行了7次重复辨识,得到的辨识结果如表3所示。

如前所述,单一次测量所对应的方程组只有3个方程而待辨识参数有4个,所以需多次测量数据来保证辨识结果的准确性。原始完整的数据为工作装置5秒动作时间内对应的500个数据点,表4给出了从这500组原始数据中在不同位置取不同量的数据对辨识结果的影响。表中最后三行数据为从500个原始数据点中每二个、三个、四个数据中均匀地提取一个数据构成的数据。其他行的数据为原始数据中按照第一列给出的区间连续提取的数据。

表4 不同数据量对辨识结果的影响

对基于连续数据辨识得到的结果,很明显数据量越多辨识结果越准确,当数据量比较小时,一方面辨识结果不准确,另一方面辨识过程中程序经常不收敛。这主要是由于连续数据量比较小的情况下,这些数据对应的工作装置构型改变量不大,所得的式(24)中的雅可比矩阵病态度很高,导致结果不收敛。在本仿真例子中,当连续数据量超过一定数据量时,如300个点时,辨识结果的准确度有较高的保证。对于间隔取值的情况,数据跨越了整个动作区间,所以构型差异度足够,在辨识过程中没有出现不收敛的情况。但表4中最后三行的数据表明,辨识结果准确度不高,可能的原因是对于连续的动力学过程数据间越紧密越能准确地代表这一过程,而过大的数据间隔增加了动力学过程歧义的可能性。

3.3 数据噪音对辨识结果的影响

在实际应用环境中,采集的数据通常包含有一定水平的噪音,这可能影响辨识结果的准确度。由于还没有实机测试数据,所以本文采用在ADAMS仿真数据上增加高斯噪音的方式来生成噪音数据,并以此来检验噪音对参数辨识结果的影响。一般而言,位移/角度等信号易于直接测量,噪音水平比较低,速度信号噪音要高一些,而加速度和力信号噪音水平最高。图5为一组仿真验证所用的叠加了噪音信息的铲斗运动及油缸力曲线。

图5 叠加了噪音信号的铲斗运动及铲斗油缸力示意图

表5给出了不同噪音水平下各参数的辨识结果。在噪音水平的设置上,速度的噪音为位移或转角的两倍,而力和角加速度的噪音水平为速度的两倍。噪音的大小为无噪音信号的最大值与最小值之差乘以噪音水平再乘以0与1之间的随机数。从表5可以看出,不同的噪音水平下质量的辨识结果都很稳定,且与真实值之间的偏差很小。随着噪音的增加,位置辨识结果与真实值之间的偏差有所增加。转动惯量的辨识值仍旧很差,并且随着噪音的增加结果出现负值的可能性大为增加。

表5 不同噪音水平下各参数的辨识结果

在本文中,参数辨识是通过式(24)方法来完成的,在矩阵的求逆中一般应用的都是最小二乘法。当噪音为白噪音时,在数据量比较大的情况下,这一方法的辨识结果可以保证比较高的准确度。

4 结论

本文研究分析了一种基于动力学建模的挖掘机铲斗及土方复合体的动力学参数辨识方法。辨识的参数包括质量、质心位置和转动惯量。通过ADAMS构建了一款挖掘机模型,并通过其生成仿真数据以检验辨识方法的效果。在保证一定数据量的条件下质量参数的辨识结果可以非常准确,质心位置也可以比较准确地获取,但转动惯量的辨识结果与真实值之间偏差很大。此外,数据应达到一定量,其覆盖的工作装置构型应具有一定的差异度,以降低方程的病态度并保证辨识结果的准确度。本文还检验了数据噪音对辨识结果的影响。检验结果表明,即使数据中包含有较高水平的高斯噪音,质量的辨识结果精度仍然可以得到保证,质心位置的准确度会随着噪音的增加有所降低。