液压挖掘机斗杆结构的拓扑优化设计
2020-01-14李建军
李建军 隋 哲
(1.沈阳理工大学 工程实践中心,辽宁 沈阳 110159;2.沈阳理工大学 机械工程学院,辽宁 沈阳 110159)
液压挖掘机广泛应用于当今的国民经济建设,是工程中必不可少的机械设备.斗杆是挖掘机的重要工作部件,其刚度和质量会直接影响挖掘机的工作性能和效率,从而影响工程的进度.目前,挖掘机的结构优化主要用于稳定整机系统的性能,很少对部分结构进行优化,针对斗杆的结构优化设计则更少.结构拓扑优化设计的实质是将求解结构最优的拓扑问题转化为在给定设计空间内找到最合理的材料分布.为此,本文拟引入结构拓扑优化技术,在不确定拓扑形状的情况下,依据部件的工作情况和优化目标等确定优化后的材料分布,进而得到能满足工作刚度要求且体积更小的斗杆结构.具体来说,以BD85W型轮式液压挖掘机为研究对象,对其实际工况进行分析并通过有限元软件建立斗杆的三维模型;应用变密度法,以三维模型设计区域网格划分后每个单元的相对密度为设计变量,以一定体积作为约束条件,以挖掘机的最大刚度为目标函数,设计结构质量更小、刚度更大的斗杆结构.
1 液压挖掘机的斗杆
BD85W型液压挖掘机的工作装置主要包括铲斗、斗杆、前动臂、后动臂、铲斗油缸、动臂油缸、调节油缸及机架(图1)[1].其各部分通过铰接方式连接.斗杆油缸的前端与斗杆的后端铰接,通过斗杆油缸的伸缩来实现斗杆的运动.前动臂的前端与斗杆的后端铰接.铲斗的尾部与斗杆的前部铰接.铲斗的挖掘动作是通过铲斗油缸的伸缩完成的,而铲斗绕铲斗杆前铰接点的转动是通过铲斗油缸和连杆来实现的.为了实现挖掘机的各种挖掘作业,通常利用连杆机构和伸缩油缸来增大铲斗的转动角度[2].
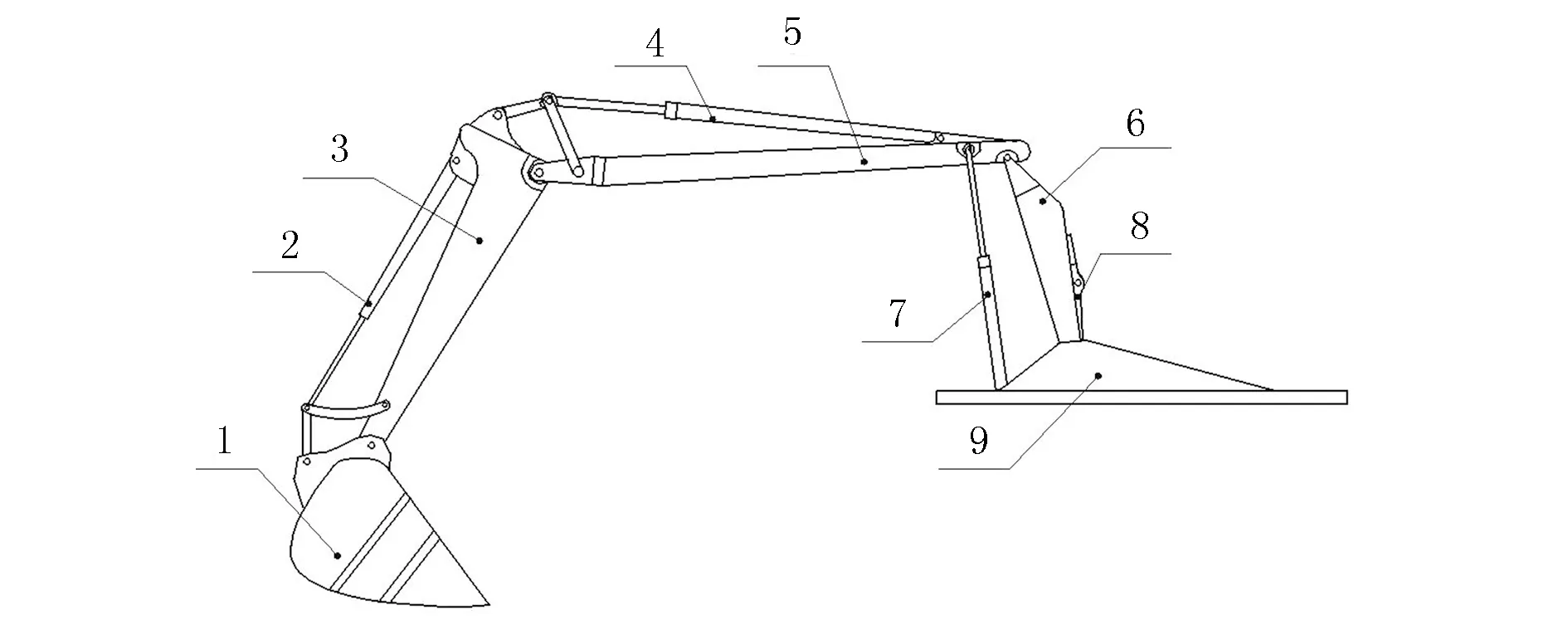
注:1—铲斗;2—铲斗油缸;3—斗杆;4—斗杆油缸;5—前动臂;6—后动臂;7—动臂油缸;8—调节油缸;9—机架.
2 斗杆的工况分析
对挖掘机工作装置进行受力分析时,一般针对其最危险工况.本文选用挖掘机斗杆的危险工况[3]进行其受力分析.液压挖掘机斗杆的典型危险工况如图2所示.此时,动臂油缸处于完全收缩的状态,而动臂处于最低点;斗杆油缸与连杆相互垂直;铲斗的齿尖位于铲斗与斗铰点连线的延长线上.
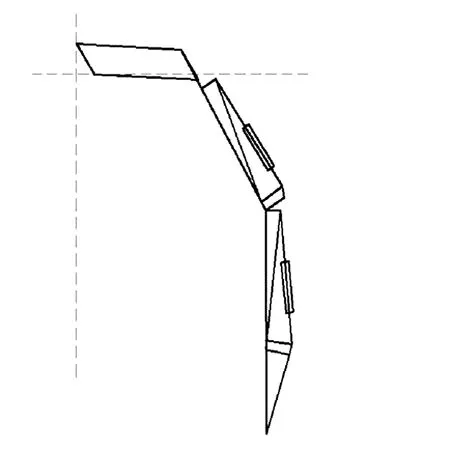
图2 斗杆的典型危险工况
2.1 斗杆的载荷
斗杆的载荷主要通过各铰点来施加.在分析斗杆载荷时需先对各铰点设定坐标,然后分析斗杆各铰点的受力(图3).

注:F为铲斗齿尖在任意工况下的切向挖掘力;θ为F与水平方向的夹角;F1、F2分别为铲斗齿尖在任意工况下垂直和水平方向的分力;G1为斗杆受的重力.
对斗杆各铰点受力进行分析时,应把所有杆件当作二力杆,通过传统算法,对典型危险工况下的斗杆受力进行分析[4]。所测得危险工况下斗杆受力值和θ角度如表1所示.

表1 斗杆危险工况下受力的值和θ角度
2.2 斗杆的约束
斗杆与动臂通过铰接的方式在图3中A点相连接.本文只分析斗杆的受力情况并对其进行优化,应固定斗杆与前动臂的铰接点E的坐标,在施加约束时只释放Z轴的旋转自由度,而对其他5个自由度加以约束[5].
3 斗杆有限元模型的建立
对斗杆进行拓扑优化前需建立斗杆的有限元模型,只有高质量的有限元模型才能使拓扑优化的结果更接近实际情况.
3.1 建立斗杆的几何模型
液压挖掘机结构较复杂,在建立几何模型时需对其进行简化,只保留斗杆的正常装配和各项功能,而省略一些不必要的特征.所建立的斗杆几何模型如图4所示.

图4 斗杆几何模型
3.2 对斗杆进行有限元网格划分
网格划分是拓扑优化的准备工作之一,也是拓扑优化的基础.其基本原则是在保证划分精度和效率的前提下,对模型进行必要的简化,以减少网格单元和储存规模,加快计算的速度,提高结果的精度.
本文根据该原则,结合斗杆的实际尺寸,选择四面体单元类型进行斗杆的有限元网格划分,得到了36 377个节点和20 128个单元.其划分结果如图5所示.

图5 斗杆的网格划分结果
3.3 设置斗杆的边界条件
网格划分工作完成后需对斗杆设置边界条件.斗杆通过铰接点(图3中E点)与前动臂连接.对该点施加约束时需对X、Y、Z方向的移动和绕X、Y轴的旋转自由度进行约束,只释放绕Z轴旋转的自由度;A点受斗杆油缸的推力作用;B点受铲斗油缸的推力作用;D点受铲斗工作时的反作用力作用.因此,A、B、D均为施加载荷点.
4 斗杆的拓扑优化
拓扑优化是一种数学优化方法,其原理是在给定的设计空间、载荷以及边界约束条件下,确定结构材料的最优分布,使结构在满足某种性能指标的情况下,具有更合理的材料分布,从而达到提升性能和节约材料的目的.常见的连体结构拓扑优化方法有很多,包括均匀法、变厚度法、变密度法等.本文通过变密度法对挖掘机的斗杆结构进行拓扑优化设计.
目前变密度法广泛应用于连体结构的优化,它将结构的材料密度视为可变的,并以每个单元的密度作为设计变量,规定单元密度为0处材料为空,单元密度为1处材料为完全保留,设计区域的单元密度在0~1之间变化.假设材料的密度与物理属性之间存在一种非线性关系,则根据相关理论可得如下数学模型:
(1)
式中:E0为单元充满材料时实际材料的弹性模量;Ei为优化迭代计算中材料第i单元的弹性模量;η为单元密度;μ为单元泊松比;μ0为单元充满材料的泊松比;α为惩罚因子.
4.1 建立模型
对斗杆的拓扑优化通常要求斗杆的刚度最大[6].材料的刚度与柔度互为倒数,优化斗杆时选用柔度作为目标函数,刚度最大则柔度最小.斗杆的拓扑优化数学模型为:
(2)
式中:Xi(i=1,2,…,n)为每个微单元的相对密度;σ为柔度;P为载荷矢量;U为节点位移矢量;n为剩余材料体积与原始材料体积之比;V1为优化区域剩余材料总体积;V0为优化区域的原始材料体积;K为结构的刚度矩阵.在优化设计中,常用应变能的大小来反映柔度大小,而应变能等于使结构变形所做的总功[7].推导可得结构的应变能C,即:
(3)
由式(3)可知,结构刚度和应变能互为倒数.可采用SIMP(Solid Isotropic Material with Penalization)插值模型的变密度法,以最大刚度为目标,以体积分数为约束条件[8-10],对斗杆进行拓扑优化分析.
4.2 拓扑优化
本文采用有限元分析软件Hypermesh中的Optistruct模块,对挖掘机的斗杆进行仿真分析.该模块可解决有限元分析中的大多数拓扑优化问题.如果在响应参数方面有特殊要求,则可根据结构的实际情况,通过编写公式方便地定义符合需要的响应参数.
斗杆的材料为16Mn,弹性模量E=2.06×105MPa,密度为7 850 kg/m3,泊松比μ为0.266,屈服强度为345 MPa.根据斗杆的典型危险工况,对斗杆施加相应载荷及边界条件,并以应变能最小为目标,以体积分数为约束条件,对斗杆的有限元模型进行拓扑优化.经过35次迭代,得到的斗杆密度分布云图如图6所示.

图6 斗杆密度分布云图
4.3 结构设计
拓扑优化结构为概念设计结构,存在形状不规则、结构不连续等缺陷,不符合加工工艺.为此,在拓扑结构材料分布模型的基础上,应对斗杆结构进行重新设计.在设计新结构时应遵循以下原则:①新结构与其相连的结构之间装配关系不变;②新结构的材料分布要尽可能接近拓扑优化的结果;③新结构要有良好的加工工艺性.根据这些原则设计的斗杆新结构如图7所示.
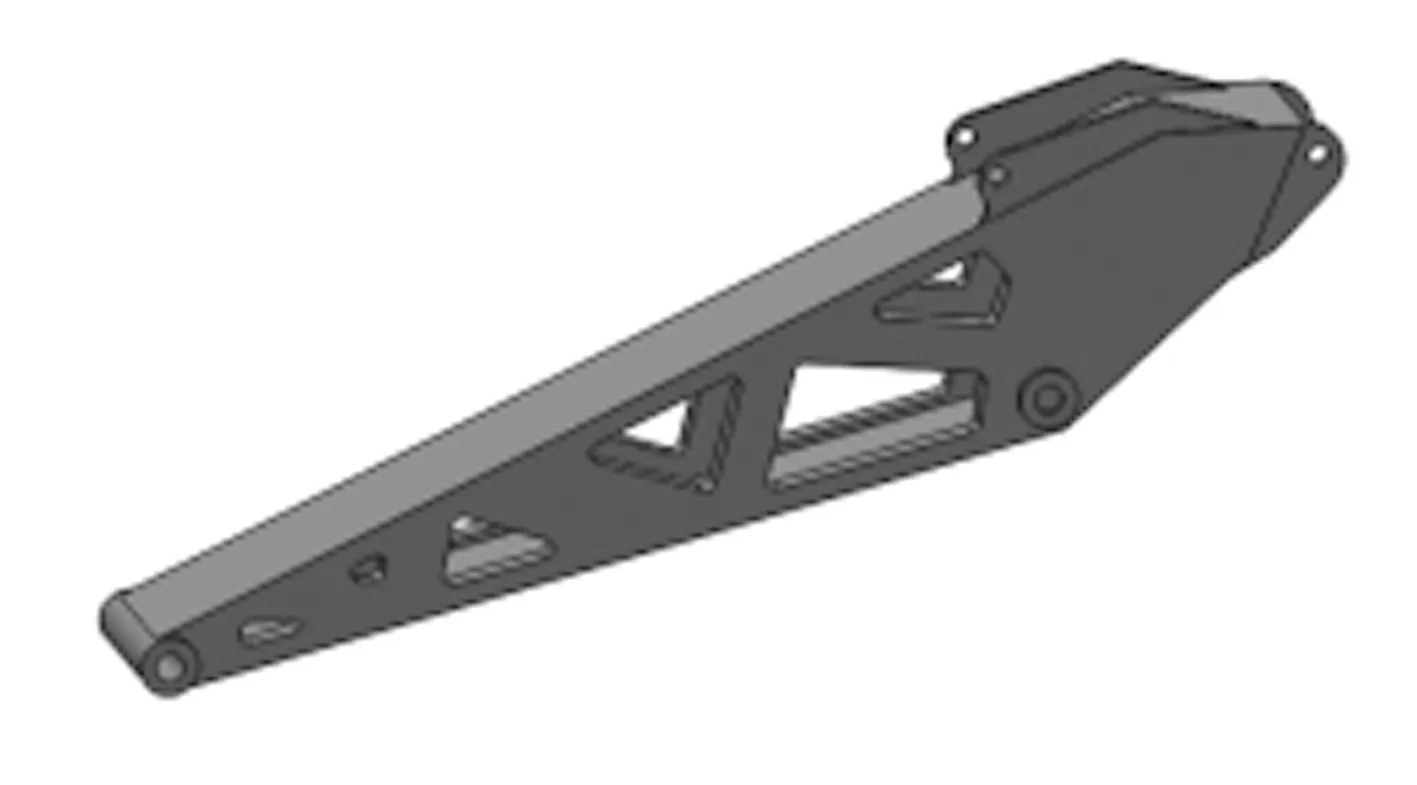
图7 新的斗杆结构模型
5 优化前后斗杆结构性能对比
对斗杆的新旧结构在危险工况下进行二次静力分析.斗杆结构优化前后的应变云图如图8所示.斗杆结构优化前后的应力云图如图9所示.结构优化前后,斗杆体积、最大变形和最大应力的变化情况如表2所示.

(a)优化前 (b)优化后

(a)优化前 (b)优化后

表2 结构优化前后斗杆体积、最大变形和最大应力的变化情况
从表2可以看出:结构优化后,斗杆的体积减少18.22%,节省了材料;斗杆的最大变形减小6.58%,增大了刚度,达到了预期目的.
6 结束语
应用变密度法的拓扑优化技术,结合有限元软件对挖掘机斗杆进行了拓扑优化.综合考虑斗杆拓扑结构的加工工艺等因素,对斗杆结构进行了优化设计.结构优化后的斗杆刚度较结构优化前有所提升,且斗杆质量更轻.该方法有利于提高产品的系列化程度和设计水平,能够为其他挖掘机斗杆的分析和优化提供参考.
