管路外表面裂纹应力强度因子研究*

周知进,闻 多,冷晓峰

(1.广西科技大学 机械与汽车工程学院,广西 柳州 545003;2.贵州理工学院 机械工程学院,贵州 贵阳 550000)

0 引言

油气管路是用来输送天然气、石油等重要能源资源,故在我国工业体系中有很重要的地位。由于使用环境恶劣,在安装和使用的过程中会有划伤[1-2]。管路在输送流体时,流体压力会给管路的内壁带来压力,裂纹尖端往往会产生很大的应力集中而让裂纹扩展[3],非贯穿裂纹逐渐变成贯穿裂纹,进而导致泄露故障,造成经济和安全方面的损失[4]。对管路应力强度因子的研究是分析裂纹体寿命的关键,这有助于我们及时对管路进行更好的安全管理[5]。管线钢断裂一般均为延性断裂,一旦达到裂纹扩展的门槛值,则裂纹的扩展很难停下来,直至管路断裂[6]。孙伟栋[7]使用ABAQUS软件得到了裂纹尖端应力随裂纹长度、深度、角度变化的规律。邓斯尧[8]使用ANSYS做分析得到了管路的三种不同裂纹的应力强度因子和J积分。崔巍等[9]人用VCCT的方法计算了裂纹尖端的能量释放率和尖端张开位移。目前对于油气管道裂纹应力强度因子随裂纹形状大小与角度变化的研究成果较少。鉴于此,从不同角度、长度、深度对初始裂纹的前缘应力强度因子变化规律以及裂纹尖端的受力情况进行研究。

1 裂纹应力强度因子基础理论

工程结构中三种失效模式中,断裂是危害最大的一种,由于工程实践的需要,断裂力学这门学科由此诞生[10]。在工程中,我们往往根据裂纹的受力特点,将裂纹分为三类(图1)。

图1 三种不同力学特征的裂纹类型

假设裂纹体为线弹性材料,则裂纹尖端附近的应力场为

(1)

其中,K代表应力强度因子,K不依赖于极坐标r和θ,应力强度因子与构件几何形状、应力作用大小和方式有关,它的存在可以衡量整个裂纹尖端附件的应力场中各点的大小。对于图1中的三种不同类型的裂纹,应力强度因子分别为K1、K2、K3。

J积分由RICE在1968年提出,随着理论体系的完善,再加上又容易被实验测定,J积分被广泛的应用于裂纹计算中。J积分在能够准确的描述裂纹尖端区域的应力应变场,其定义如下[11]:

(2)

J积分的局限在于仅限于单裂纹问题,M积分法在处理多裂纹问题中有着很大优势。M积分法的物理意义为缺陷自相似膨胀期间的势能变化。其定义为:

(3)

式中:Γ表示两条逆时针围绕裂尖的积分路径,W是应变能密度因子。

本文计算三种不同类型裂纹的应力强度因子是通过M积分法来计算得到的[12]。

式中:E为材料弹性模量,V为材料泊松比。

T应力又被称作裂纹尖端第二项非奇异项,当裂纹周边处于低约束的情况时,T应力的正负值可以影响材料的断裂韧度[13],也能改变裂纹起始扩展角的大小。

2 裂纹体三维模型建立和仿真分析

2.1 管路的基本参数

管路的基本参数:壁厚为70 mm,长度为1500 mm。管材选用结构钢为材料,弹性模量E为2.1×105MPa,泊松比设为0.3。

2.2 无裂纹管路的有限元仿真

将三维模型导入到ABAQUS软件中,赋予材料属性。网格单元设置为C3D8R六面体单元,网格单元大小为26,创建静力分析,内壁施加21 MPa的压强,两个端面设置完全固定支撑。

提交分析后,得到的应力云图如图2所示。可以看出,管路的外表面和内表面的应力分布都比较均匀,靠近两端支撑的内外表面应力都相对较小,在稍远离两端的内外表面应力分布几乎一致。外表面的应力值在45 MPa左右。

图2 管路的应力云图

2.3 三维初始裂纹的引入和网格划分

在ABAQUS中提交的应力和网格数据以inp的文件的形式导入到三维裂纹扩展分析软件中,并保留带有应力边界条件面的网格,在图3(a)所示的位置中插入裂纹,并将单元环半径设置为2.5 mm(作为一个通用的经验法则,通常来说裂纹求解在有限元中要获得精确的结果,单元的尺寸要十倍小于要划分的网格的特征尺寸)。

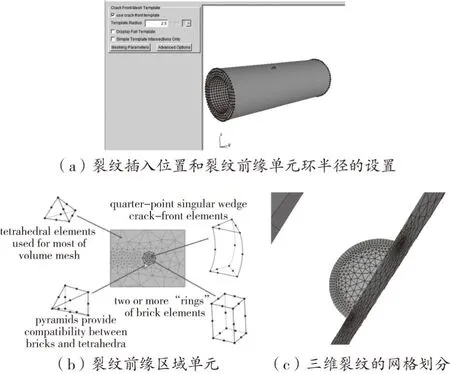
图3 网格划分

如图3(b)所示,在划分体网格时会在模板内部围绕裂纹前缘生成规则的三圈单元环。其中,最内侧是 1/4 节点的楔形单元,外面两圈或多圈是二阶的六面体单元环,过度区域采用金字塔型单元,远离裂纹尖端区域的地方采用正常尺寸的单元。生成的三维裂纹网格划分如图3(c)所示。

3 外表面裂纹角度对应力强度因子的影响

通过对裂纹的旋转来实现倾斜角的改变,选用图3中的裂纹。本章节定义裂纹和管路表面的夹角为θ,分别取90°、75°、60°、45°。由于裂纹两端附近往往是整个裂纹前缘中受力最大的,选取裂纹两端附近的应力做研究,裂纹两端的应力云图如图4所示,其周围区域呈阶梯状下降。随着倾斜角度的增加应力集中更大,但是到θ为60°之后裂纹两端的受力开始减小。

图4 裂纹插入不同角度的裂纹尖端应力云图

如图5所示是θ=90°的裂纹得到的前缘的K1值,X轴代表裂纹前缘两端点之间归一化的值。裂纹的K1值在两端的值最大,越到尖端越小。在液压直管中,径向直裂纹所受的剪应力很小,所对应的K2和K3可以忽略不计,所以在直裂纹中,前缘的J积分的变化趋势和K1相同。

图5 θ=90°时裂纹前缘的K1值

在直管中的直裂纹,可以近似看成单纯的Ⅰ型裂纹问题。但裂纹会随着插入角度的变化使得三种应力强度因子都发生变化,液压直管中的斜裂纹必须看成是三种裂纹的混合问题。

根据表1的数据,裂纹前缘K1会随着倾斜角度的增加而减小,且下降速率变快。θ=75°的K1如图6(a)所示,斜裂纹从两端到内部的一小段距离先上升,然后到中点之前下降,同时随着裂纹倾斜角的增大,这种上升趋势会越来越明显,前缘的应力强度因子分布越来越像一个M形。随着倾斜角的增加,裂纹两端的K1值下降速度大于尖端处,到θ=60°时裂纹尖端处的值更大。

表1 四个不同角度的裂纹参数值

图6 θ=75°裂纹的应力强度因子

K2和K3最大值和最小值的绝对值都随着裂纹的倾斜角的增加而增加。所有斜裂纹前缘K2的值两侧对称分布,呈现处“两边大中间小的”趋势,尖端处的K2值大约是两端处的负2倍,裂纹2前缘的K2值如图6(b)所示。所有斜裂纹前尖端处K3的值为0,A端到B端都呈比较平滑的上升趋势,裂纹两侧K3值是相反数,裂纹2的K3值如图6(c)所示。

前缘J积分随倾斜角增大而减小。但由于K2和K3的值也比较大,所以J积分的变化趋势和K1稍有不同,裂纹2的J积分如图6(d)所示。

与J积分相反的是T应力的值随倾斜角度线性增加。在倾斜角较小时,前缘所有节点的T应力的值都为负数,为倾斜角为50°时所有T应力的值增长到正数。

4 外表面裂纹深度对应力强度因子的影响

如表2所示,裂纹a=25 mm时,b分别取15 mm、20 mm、25 mm、30 mm、35 mm,b=25 mm时的应力云图见图3(a),其余插入的四个裂纹两端的应力云图如图7所示。从图中可以看出,其应力随着深度的增加而变大。

表2 不同深度的裂纹的应力强度因子

图7 不同深度裂纹尖端应力云图

J积分随着b值的增加而增加,且随深度的变化速率和前缘的分布规律与K1一样。T应力的值随着裂纹深度b的增加而线性减小。

5 外表面裂纹长度对应力强度因子的影响

表3所示的裂纹b值都为25 mm,a值分别取15 mm、20 mm、25 mm、30 mm、35 mm,a=25 mm时的应力云图见图3(a),其余插入的四个裂纹两端的应力云图如图8所示。可以发现裂纹两端的应力并不一定随着裂纹长度的增加而增加,且随长度增加的变化幅值也很小,这是由于裂纹长度的改变在本案例中边界条件不会影响太多裂纹的受力[13]。

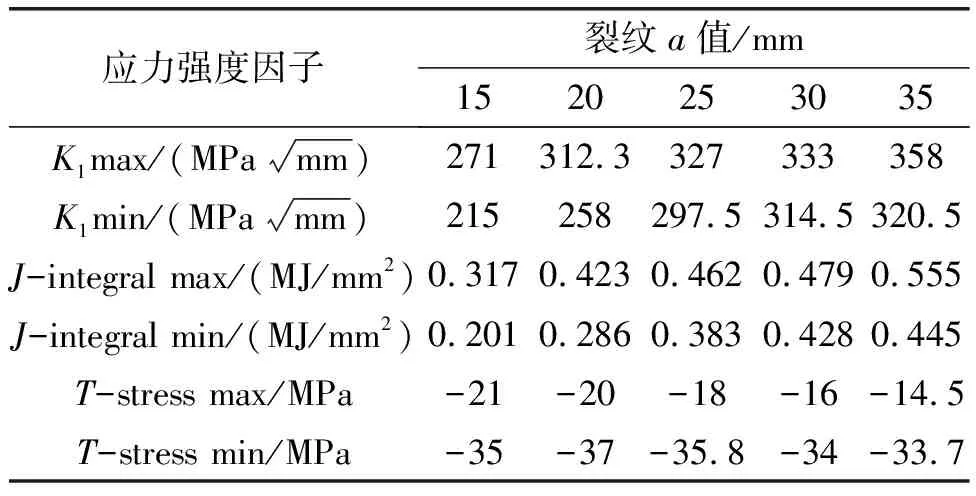
表3 不同长度裂纹的应力强度因子

图8 不同长度的裂纹尖端应力

如表3所示,K1的值随长度增大而变大。在裂纹长度半径a小于30mm时,K1的最大值都在两端处。但两端K1的值随长度增加的速率很缓慢,尖端的K1增加速率则较大,到裂纹长度稍长时,尖端处的K1值就变成了前缘最大。J积分和T应力变化趋势同K1。

6 结论

本文探讨不同角度、深度、长度对椭圆形外表面裂纹的尖端应力分布和裂纹应力强度因子的影响。得出以下结果:

1)同样形状裂纹随着倾斜角的增大,会让裂纹前缘受力增加,同时增长的还有K2和K3以及T应力,但K1和J积分的值会大幅度减小。

2)直裂纹插入深度的增加会增加裂纹前缘附近的应力、K1、J积分值。K1尖端处的增长率则相对两端处缓慢,随着深度的增加K1分布呈现两头大中间小的趋势。T应力随着深度的增加而线性减小。

3)直裂纹长度的增加不一定会让裂纹前缘的受力更大,随着长度的增加,中点处K1、J积分和T应力会增加,但两端处增长相对缓慢,随着长度的增加会使其分布呈现两头小中间大的趋势。