基于PSO-Elman 神经网络的井底风温预测模型

2024-03-01程磊李正健史浩镕王鑫

工矿自动化 2024年1期

程磊，李正健，史浩镕，王鑫

（1. 河南理工大学安全科学与工程学院，河南焦作 454003；2. 河南理工大学煤炭安全生产与清洁高效利用省部共建协同创新中心，河南焦作 454003）

0 引言

随着我国煤炭开采量的持续增长，矿井开采深度逐渐增大，井下风温升高，许多矿井的开采条件恶化，热害问题日益突出，严重制约着深部煤炭资源的安全高效开采。为准确评估矿井热害程度，制定科学合理的降温措施，改善井下高温作业环境，矿井风温预测至关重要。

近年来机器学习在岩爆指标预测[1-2]、瓦斯涌出量预测[3-4]、瓦斯渗透率预测[5-6]等方面广泛应用，取得了较好的成果，在矿井风温预测方面也有学者进行了研究。高佳南等[7]通过粒子群优化（Particle Swarm Optimization，PSO）算法对支持向量回归（Support Vector Regression，SVR）参数进行优化，建立了矿井淋水井筒风温预测模型，提高了风温预测精度。纪俊红等[8]使用网格搜索算法和K 折交叉验证优化XGBoost 模型，建立了井底风温预测模型，解决了XGBoost 模型参数多、复杂性大的问题。吕品等[9]首次建立了基于BP 神经网络的矿井淋水井筒风温预测模型，为矿井风温预测提供了新思路。张翔等[10]建立了基于PSO-BP 的淋水井筒风温预测模型，通过PSO 算法优化BP 神经网络，解决了BP 神经网络易陷入局部最优的问题。马恒等[11]结合模糊方法和人工神经网络，建立了淋水井筒的T-S 模糊神经网络风温预测模型，提高了预测模型的精度。段艳艳[12]利用支持向量机（Support Vector Machine, SVM）强大的非线性能力，建立了基于SVM 的矿井风温预测模型。张群[13]建立了基于改进BP 神经网络的井底风温预测模型，通过trainlm 函数对 BP 神经网络进行优化，解决了BP 神经网络收敛速度慢的问题。

上述研究为井下热害防治提供了理论依据。在井下风温预测过程中，大多数学者采用具有强大非线性处理能力的BP 神经网络，但其预测精度受学习样本数量的影响，且容易陷入局部最优。Elman 神经网络是一种动态的前馈性神经网络，其隐含层中增加了一个承接层，可认为是延时算子，主要用于隐含层前一时刻输出值的记忆和存储。与BP 神经网络相比，延时算子使Elman 神经网络具备局部记忆能力，提高了神经网络的稳定性和动态适应能力。但Elman 神经网络仍然存在收敛速度过慢、易陷入局部最优的问题。本文采用PSO 算法对Elman 神经网络的权重和阈值进行优化调整，建立了基于PSO-Elman神经网络的井底风温预测模型，并通过19 个矿井的实测数据[8,10-11,14]进行验证。

1 基于PSO-Elman 的井底风温预测模型

1.1 Elman 神经网络

Elman 神经网络主要由输入层、隐含层、承接层和输出层构成，如图1 所示。承接层属于内部反馈连接，其神经元与隐含层神经元一一对应。

图1 Elman 神经网络结构Fig. 1 Elman neural network structure

Elman 神经网络的非线性空间函数为[15-18]

式中：x(k)为第k次循环隐含层输出；f(·)为隐含层的激励函数；w1，w2分别为输入层到隐含层、承接层到隐含层的连接权重矩阵；xc(k)为第k次循环承接层输出，对应第k-1 次循环隐含层输出；u(k-1)为网络输入；b1，b2分别为输入层到隐含层、隐含层到输出层的阈值；w3为输出层的权重矩阵；y(k)为输出层输出，即预测的风温；h(·)为输出层的激励函数。

1.2 PSO 算法

PSO 算法是一种全局优化算法，通过个体间相互作用对可行解空间进行迭代搜索，最终获得最优解[19-21]。PSO 算法流程如图2 所示。首先对参数和粒子进行初始化，计算适应度，更新粒子速度和位置，更新种群；然后引入变异算子，重新初始化粒子，计算新粒子适应度；最后确定个体最优解和全局最优解，当达到设定的迭代次数时结束迭代。

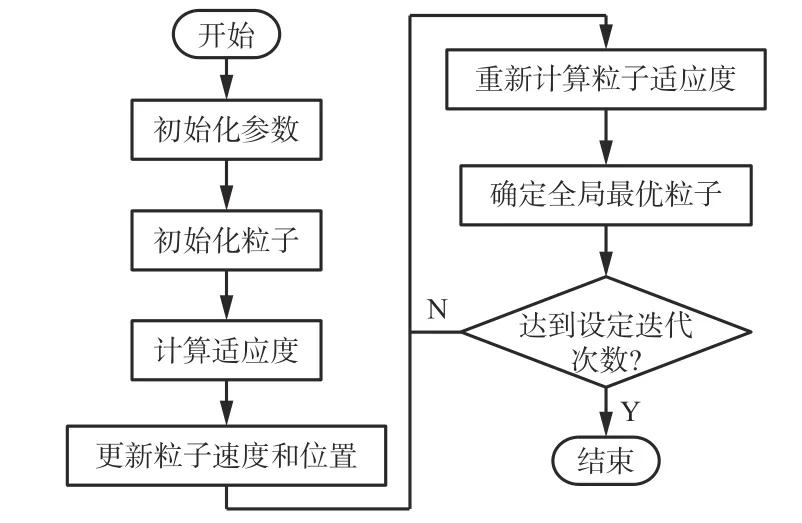
图2 PSO 算法流程Fig. 2 Flow of particle swarm optimization algorithm

粒子速度和位置更新公式为

1.3 PSO-Elman 模型流程

利用PSO 算法优化Elman 神经网络，建立井底风温预测模型，其流程如图3 所示。

1）确定Elman 网络各层结构。影响井底风温的主要因素有4 个，分别为入风相对湿度、入风温度、地面大气压力和井筒深度，因此输入数据为4 维。输出为井底风温，因此输出数据为1 维。设计Elman网络结构为4-9-1，即输入层节点个数为4，隐含层节点个数为9，输出层节点个数为1。

2）归一化处理。对样本数据进行归一化处理，生成模型训练样本集。

3）新建Elman 网络。训练函数选用traingdm，输入层和输出层的传递函数分别选用tansig，purelin。算法参数设置：PSO 算法最大迭代次数为100，种群数目为20，惯性权重ω=1.2，学习因子c1=c2=2，最大更新速度为1，最小更新速度为-1。

4）产生初始粒子。产生一个初始种群，初始化粒子的速度，计算适应度，并初始化粒子全局最优解和局部最优解。

5）迭代寻优。更新粒子速度和位置，更新种群；引入变异算子，重新初始化粒子，计算新粒子适应度，确定局部最优解和全局最优解，将每代最优解记录到数组中。

6）训练Elman 神经网络。设置最大迭代次数为100，训练目标最小误差为10-5，学习速率为0.1。

7）预测井底风温。用训练好的模型进行井底风温预测。

1.4 预测结果评估

采用平均绝对误差（Mean Absolute Error，MAE）、平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）、均方误差（Mean-Square Error，MSE）和决定系数R2对井底风温的预测结果进行评价。

MAE 是预测值误差实际情况的反映，其计算公式为

式中：n为数据个数；Pj为预测值；Aj为测量值。

MAPE 是相对误差度量值，其计算公式为

MSE 是预测值与测量值之差的平方的期望值，其值越小，表示预测模型的精度越高。MSE 计算公式为

决定系数反映测量值与预测值的分布趋势，其值越接近1，表示相关性越强。决定系数计算公式为

2 实验及结果分析

2.1 样本数据来源

将入风相对湿度、入风温度、地面大气压力和井筒深度作为模型的输入数据。风流自井口流入井下，地面风流温度和地面大气压力影响井筒风温。自压缩热是井底最主要的热源，空气的自压缩热对井筒风温影响较大，井筒深度与风流压缩密切相关，因此，井筒深度也影响井筒风温。井筒一般有淋水现象，风流和井筒淋水间存在热湿交换。地面入风的相对湿度影响风流与淋水巷道的湿交换程度。

选用19 个矿井的65 组数据作为样本数据。其中前55 组数据作为训练集，用于构建预测模型；后10 组数据作为测试集，用于检验模型预测效果。部分样本数据见表1。

表1 样本数据Table 1 Sample data

2.2 预测结果分析

在相同的训练集下，比较Elman 模型与PSOElman 模型的收敛速度，二者的进化曲线如图4 所示。可看出Elman 模型迭代90 次后收敛，而PSOElman 模型迭代41 次后收敛，说明PSO-Elman 模型收敛速度更快。

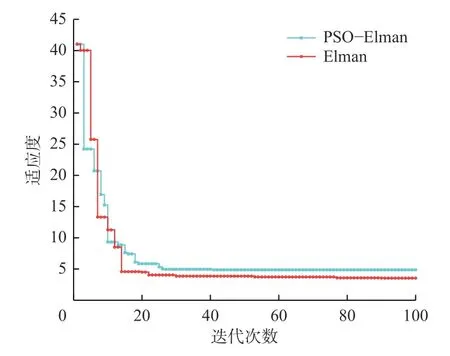
图4 预测模型的进化曲线Fig. 4 Evolution curves of prediction models

为验证基于PSO-Elman 的井底风温预测模型的预测效果，将BP 神经网络模型、SVR 模型、Elman模型与PSO-Elman 模型进行比较。BP 神经网络模型利用Matlab 软件自带的BP 神经网络工具箱进行预测，BP 神经网络结构为4-7-1；SVR 模型的惩罚因子C=22.627 4，核函数参数g=0.031 3；Elman 模型的神经网络结构为4-8-1；PSO-Elman 模型的神经网络结构为4-9-1。利用相同的训练数据集和测试数据集，比较4 种模型的预测精度，结果见表2。分析可知，BP 神经网络模型、SVR 模型、Elman 模型与PSO-Elman 模型的相对误差范围分别为-6.01%～17.02%，-9.52%～1.41%，-7.91%～0.70%，-6.55%～1.12%，PSO-Elman 模型的相对误差最小，预测效果最好。

表2 4 种模型的井底风温预测结果及误差Table 2 Prediction results and errors of bottom air temperature of four models

4 种井底风温预测模型在测试集上的预测结果和误差分别如图5、图6 所示。从图5 可看出，相比于其他模型，PSO-Elman 模型的预测值与真实值曲线更为接近，说明其预测效果更好。从图6 可看出，PSO-Elman 模型的预测误差最小，说明该预测模型的准确性和可靠性最高。

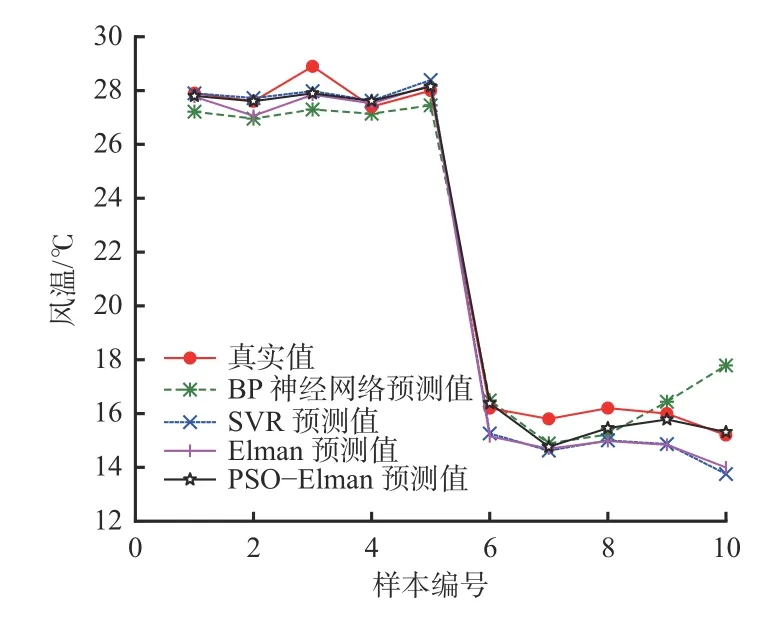
图5 4 种预测模型在测试集上的预测结果Fig. 5 Prediction results of four prediction models on test set

图6 4 种预测模型在测试集上的预测误差Fig. 6 Prediction errors of four prediction models on test set

4 种预测模型的评估指标见表3。可看出，与BP 神经网络模型、SVR 模型和Elman 模型相比，PSO-Elman 模型预测误差更低，MAE，MSE，MAPE分别为0.376 0 ℃，0.278 3，1.95%。4 种模型的决定系数R2非常接近1，表明预测模型具有良好的预测效果。实验结果表明，PSO-Elman 模型具有较高的稳定性和准确性。