基于CEL方法的瓷砖智能化铺贴质量数值分析

2024-03-01吴楷张艳荣孔祥明张浩楠李大林雷霆

中南大学学报（自然科学版） 2024年1期

吴楷，张艳荣，孔祥明，张浩楠，李大林，雷霆

(1.北京交通大学土木建筑工程学院，北京，100044；2.清华大学土木工程系，北京，100084)

在建筑工程中，瓷砖铺贴是最适合应用机器人技术的环节之一[1-4]，相关研究受到国内外广泛关注[5-11]。APOSTOLOPOULOS等[5]提出了可全方位移动的地砖安装机器人，搭载激光三角测量系统进行导航和定位，并采用高分辨率摄像机评估安装质量。NAVON[6]利用图形仿真系统研制了一款采用六自由度机械臂的地砖安装机器人，并开发了一套电脑视觉系统实现瓷砖的高精度安装和缺陷识别，其铺贴效率是人工铺贴的2～5倍。柳洪义等[7]研发的瓷砖机器人通过激光测距传感器和测量程序检测壁面与地表状况，并精准控制涂料厚度和瓷砖铺贴位置，可以在10 s内完成长度×宽度为150 mm×150 mm瓷砖的铺贴。刘侃[8]设计的导轨移动式瓷砖铺贴机器人集成了免光照影响的空间定位技术和多段路径规划的平滑铺贴模式，较人工铺贴缩短工时20.9%。LI等[9]提出了一种基于自适应视觉的瓷砖机器人控制方案，实现了在无标定摄像机和有限视野的情况下瓷砖的自动拾取与铺贴，极大提高了瓷砖机器人的自主能力。WANG等[10]提出了一种基于视觉测量的瓷砖位置补充算法，可对瓷砖的铺贴质量进行在线评估。许世斌[11]设计了一款地砖自动化涂浆机，可连续完成水泥浆搅拌和涂抹2个工序，节省近50%的时间并降低施工空鼓率至0.1%。既有文献主要关注瓷砖铺贴机器人中不同模块的功能强化和一体化设计，但有关机器人施工工艺参数对瓷砖铺贴质量影响的研究较少。为此，本文建立瓷砖-瓷砖胶-混凝土流固耦合施工模型，针对机器人施工工艺参数对瓷砖铺贴质量的影响开展研究。

1 基本理论

拉格朗日法和欧拉法是连续介质力学中用于描述材料运动的2种基本算法，其中，前者主要用于固体力学领域的有限元模拟，可准确描述物体边界运动，但在模拟大变形时易出现网格畸变而降低精度；后者主要用于流体力学领域，计算流体流动等极端变形问题，但无法精确地捕捉物体的边界信息[12]。这两者均遵循质量守恒定律、动量守恒定律和能量守恒定律，分别采用物质时间导数和空间时间导数的形式表达[13]，如表1所示。欧拉方程可统一成一般的守恒形式，如式(1)所示。NOH[12]提出了欧拉-拉格朗日方法(CEL方法)，该方法结合了这两者的优势，可用于多组件复杂流固耦合结构的模拟[14-16]，该方法将式(1)拆分成式(2)和式(3)。

表1 守恒方程Table 1 Conservative equations

式中：Φ为通量函数；S为源项。

2 模型建立

2.1 瓷砖胶屈服变形试验

首先，将直径为60 mm、高度为20 mm的圆筒模具置于湿润的SiO2玻璃板(长×宽×厚度为200 mm×200 mm×15 mm)中心；然后，将拌合均匀的德高TTB I型瓷砖胶(水胶比为6:25)倒入圆筒模具中并抹平，随即垂直、平稳地提起圆桶模具，将另一玻璃板(重0.2 N)水平置于瓷砖胶顶部，此时瓷砖胶未变形；最后，对玻璃板均匀施加2 N荷载；待瓷砖胶停止变形后记录其底部直径，如图1所示。同样，依次记录荷载为4 N和6 N时瓷砖胶的底部直径。

图1 瓷砖胶屈服变形试验结果Fig.1 Experiment result of the yield deformation of tile adhesive

2.2 瓷砖胶屈服变形模型与验证

有研究指出，线性Drucker-Prager模型通过非圆形屈服面来反映不同的三轴拉伸和压缩屈服强度、偏平面上的塑性流动以及不同的剪胀角和摩擦角，可用于模拟新拌砂浆和混凝土[17-18]。线性Drucker-Prager模型主要由屈服面函数和流动势函数等构成[19]，分别如式(4)和(5)所示。

式中：F为屈服面函数；为偏应力；q为等效Mises应力；k为三轴拉压屈服应力比；r为偏应力第三不变量；p为等效压应力；β为s-p平面上屈服面的倾角，即材料的摩擦角；d为s-p平面上屈服面的截距，即材料的黏聚力；G为塑性流动势能；ψ为s-p平面上的剪胀角。

基于CEL方法，建立瓷砖胶屈服变形模型，如图2所示。图2中，从上到下依次为顶部玻璃板、瓷砖胶和底部玻璃板。采用刚体模拟玻璃板；采用欧拉域模拟瓷砖胶，其本构方程为Drucker-Prager模型，物理和力学性能参数如表2所示。在顶部玻璃片上分别施加2、4和6 N的均布荷载，计算瓷砖胶的底部直径。

图2 瓷砖胶屈服变形模型Fig.2 Model of the yield deformation of tile adhesive

表2 瓷砖胶的物理和力学参数Table 2 Physical and mechanical parameters of tile adhesive

图3所示为瓷砖胶底部直径的模拟结果与试验结果对比。由图3可以看出，瓷砖胶底部直径的模拟结果与试验结果基本一致，最大相对误差仅为-1.98%，证明了本研究所用的CEL流固耦合模型的可靠性。

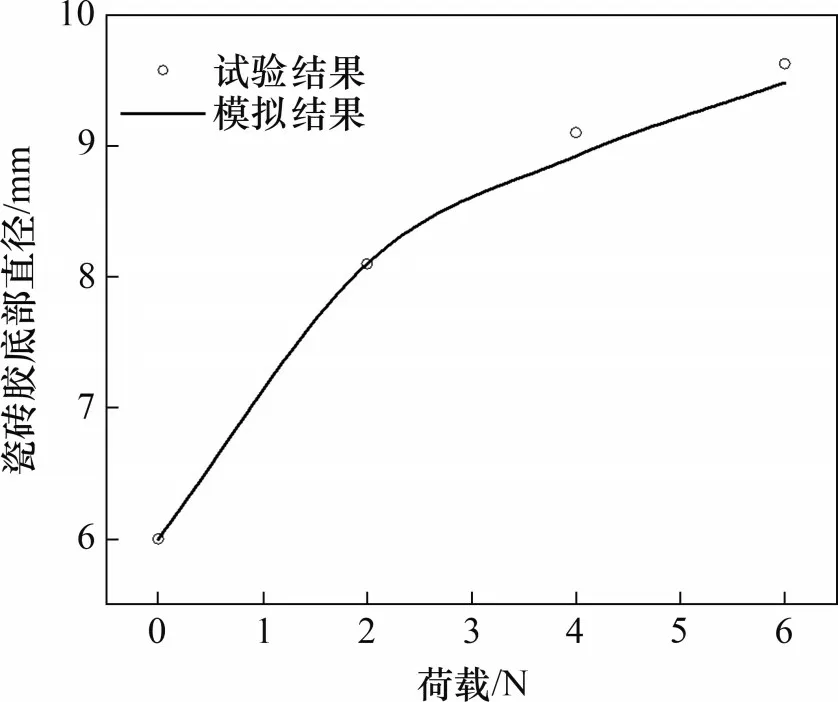
图3 瓷砖胶底部直径的模拟结果与试验结果对比Fig.3 Comparison between numerical and experimental results of the diameter of the bottom tile adhesive

2.3 瓷砖-瓷砖胶-混凝土流固耦合模型

参照文献[20]中地砖铺贴机器人(图4)的工作模式，建立瓷砖-瓷砖胶-混凝土CEL施工模型，包括瓷砖胶布料和瓷砖调平2个子模型，如图5所示。布料模型由欧拉域和混凝土基层组成，用于分析布料方式对瓷砖胶变形的影响；调平模型由瓷砖、欧拉域和混凝土基层组成，用于分析布料管数、荷载类型对瓷砖铺贴质量的影响。根据GB 50209—2010《建筑地面工程施工质量验收规范》要求[21]，依次选取瓷砖回弹量、瓷砖-瓷砖胶接触面积、瓷砖胶-混凝土基层接触面积和缺陷分布等指标表征瓷砖的铺贴质量。

图4 地砖铺贴机器人[20]Fig.4 Tiling robot[20]

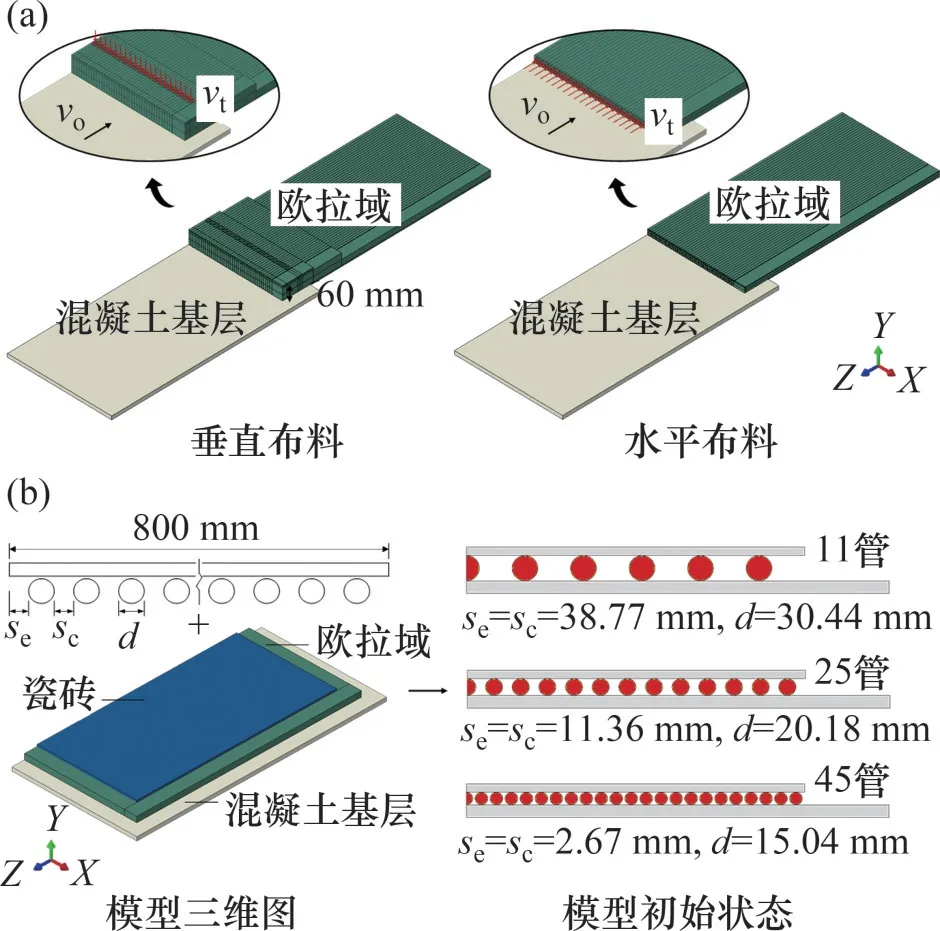
图5 瓷砖-瓷砖胶-混凝土CEL施工模型Fig.5 CEL construction models of tile-adhesive-concrete

瓷砖和混凝土基层的长×宽×厚度分别为0.8 m×0.8 m×0.01 m和1.0 m×1.0 m×0.015 m。瓷砖胶的设计体积取0.006 4 m3，并代入式(6)计算出浆口的尺寸。由于机器人采用连续方式布置瓷砖胶，布料模型中瓷砖胶的长度取0.8 m(以布料1块瓷砖的长度为例)，调平模型中瓷砖胶的长度取0.9 m(考虑相邻瓷砖胶的影响)。欧拉域体积满足覆盖瓷砖胶变形区域的要求即可。

式中：n为布料管数；V为瓷砖胶设计体积。

瓷砖和混凝土基层均模拟为刚体，分别由11万个和17万个实体单元组成。瓷砖胶设为欧拉体，对应的欧拉域分别由250万个(布料模型)和590万个(调平模型)欧拉单元组成。以“硬”接触和“罚”接触(摩擦因数为1)模拟瓷砖胶与瓷砖、瓷砖胶与混凝土基层间的法向和切向相互作用。瓷砖和混凝土的密度分别为2 400 kg/m3和2 300 kg/m3，瓷砖胶的材料参数如表2所示。

布料模型中瓷砖胶的布料管数为40根，如图5(a)所示。出浆口的移动速度和瓷砖胶的出浆速度均设置为0.25 m/s，但两者方向相反。调平模型中，瓷砖胶的布料管数取11、25和45根，如图5(b)所示。混凝土基层设置固结约束，瓷砖胶纵向两端设置对称约束。在瓷砖顶面施加3种位移调平荷载(图6)：直压荷载(下压至瓷砖胶的厚度为10 mm，加载2 s，简称为VC模式)、先直压荷载(10 mm，加载2 s)后垂直振动荷载(0.025 mm，40 Hz，持续5 s，简称为VV模式)、先直压荷载(10 mm，加载2 s)后剪切振动荷载(0.025 mm，40 Hz，持续5 s，简称为SV模式)。为提高计算效率，上述模型均为半模型，在对称面设置对称约束。计算时所有模型均施加重力均布荷载。

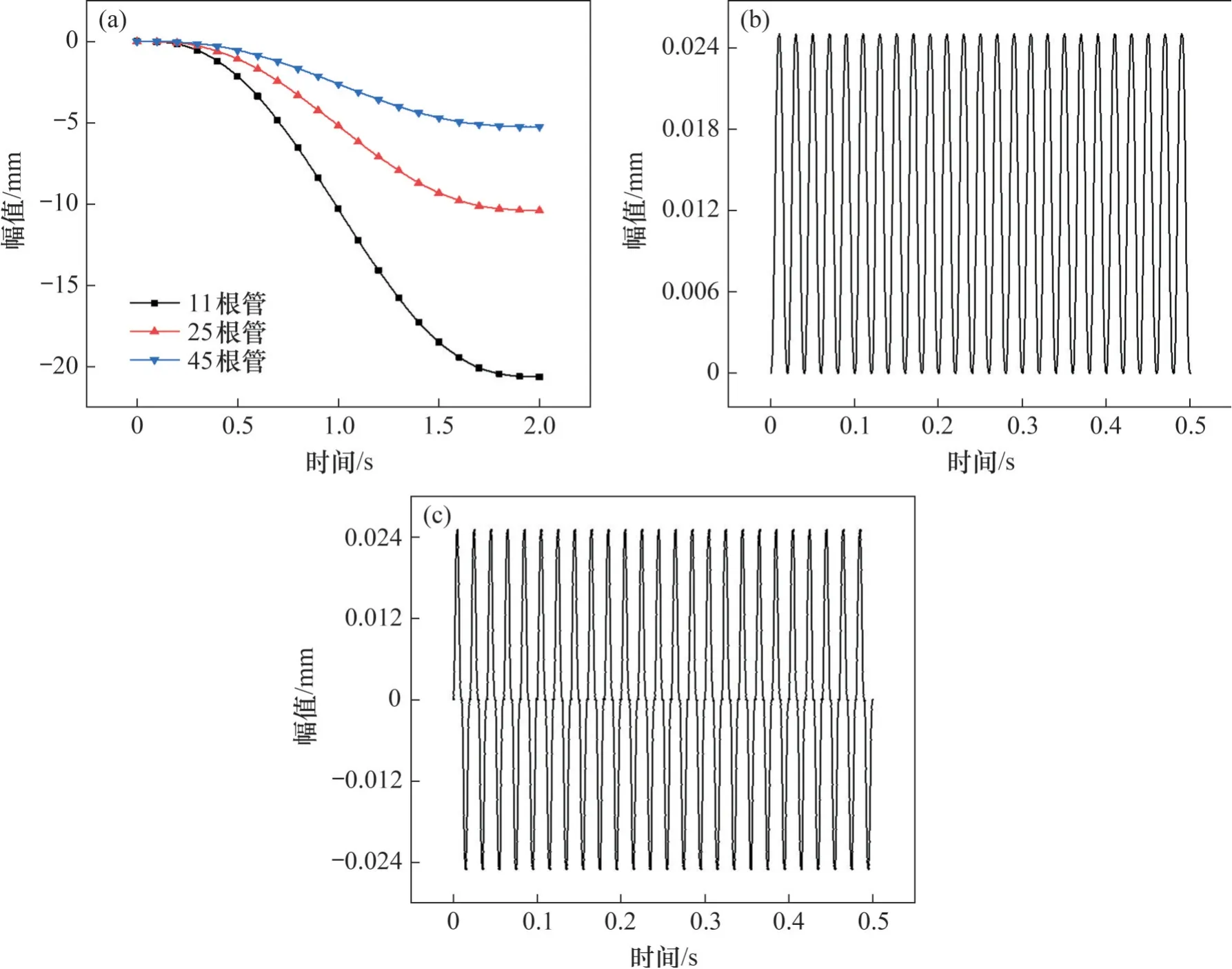
图6 荷载幅值曲线Fig.6 Amplitude curves of loads

3 结果与讨论

3.1 布料方式的影响

图7所示为水平和垂直布料方式下瓷砖胶的塑性应变云图。由图7可看出，采用水平布料时，瓷砖胶基本保持稳定的拟圆柱态，呈等间距分布，塑性应变几乎为0；采用垂直布料时，瓷砖胶与基层接触后发生弯折，塑性应变高达0.75；瓷砖胶的形态发生明显改变，多坍塌为半圆柱状，瓷砖胶间距缩小。

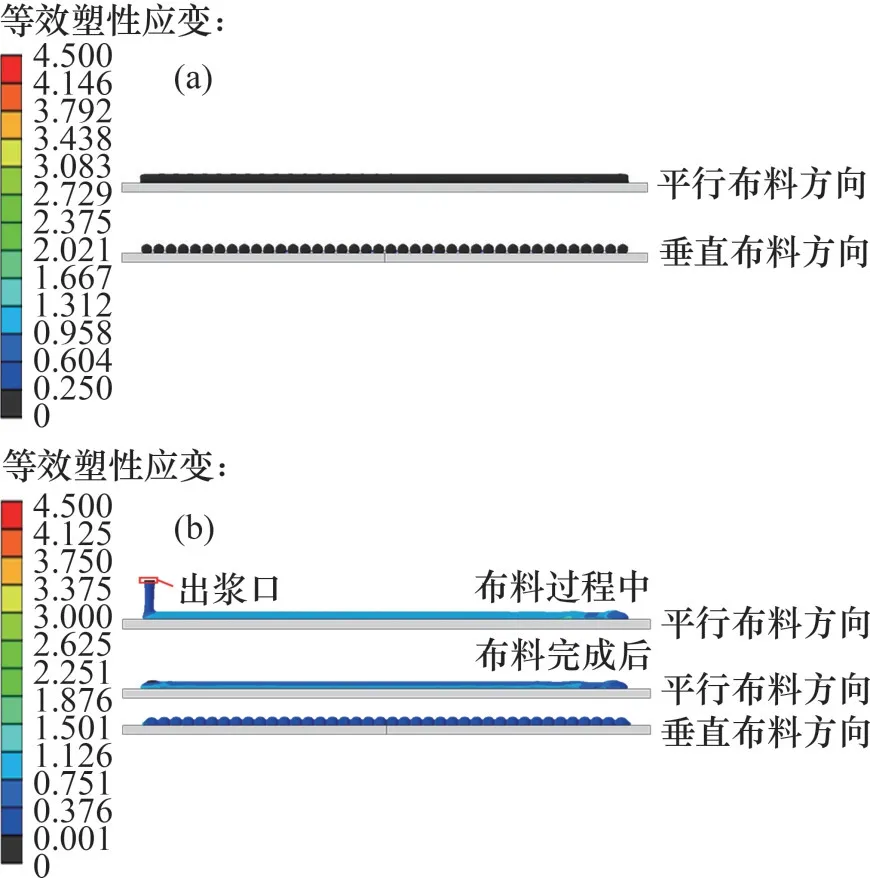
图7 水平和垂直布料方式下瓷砖胶等效塑性应变云图Fig.7 Contour plots of the equivalent plastic strains of tile adhesive applied horizontally and vertically

在瓷砖胶布料过程中，其塑性应变主要取决于材料的屈服应力、重力以及基层摩阻力等。垂直布料时，瓷砖胶接触基层前即在重力作用下产生一定量的屈服变形(图7(b))，接触基层后动能转变为塑性变形能，瓷砖胶形态相应发生较大改变(坍塌)，瓷砖胶间距缩小。而采用水平布料时，瓷砖胶的重力与基层支撑力相抵，瓷砖胶与基层相对静止(出浆口移动速度与瓷砖胶的出浆速度大小相等但方向相反)，轻小的基层摩阻力不足以引起瓷砖胶屈服变形。因此，在整个水平布料过程中，瓷砖胶基本保持原形态不变。

此外，水平布料后的瓷砖胶体积为0.006 4 m3，即与设计体积(0.8 m×0.8 m×0.01 m)相等；而垂直布料后的瓷砖胶体积仅为0.006 26 m3，这主要是瓷砖胶出浆速度与出浆口移动速度不匹配所致。

3.2 布料管数的影响(水平布料，直压荷载)

3.2.1 竖向位移与竖向力

在直压加载(VC模式)过程中，不同布料管数时瓷砖竖向位移和竖向力随时间的变化如图8所示。图8中，竖向位移为负表明瓷砖下移，竖向力为正代表瓷砖受拉，负值代表受压。按照图6所示的直压加载模式，瓷砖竖向位移在2 s内逐渐增加至目标位移D1并保持稳定；卸载后位移轻微波动，随后保持稳定位移D2。相应地，瓷砖由受拉逐渐转变为受压，且压力缓慢增大，待竖向位移增至Ds时压力迅速增加并逐渐保持为稳定值Pm；卸载后瓷砖竖向力立即恢复至0 N。随布料管数增加，瓷砖压力急剧增大的时间点Ts明显缩短，而D1与D2的差值以及最大瓷砖压力Pm基本不受影响，分别为0.165 mm和3.40 kN。

图8 不同布料管数时瓷砖的竖向位移和竖向力随时间的变化Fig.8 Variations of the vertical displacement and vertical force of tile with time under various rows of adhesive extrusion

众所周知，在直压加载过程中，瓷砖的竖向位移与瓷砖胶的竖向变形量相等。瓷砖胶在外力作用下发生弹性变形和塑性变形(对应D1)；外力卸载后弹性变形立即恢复，仅残留塑性变形(对应D2)，D1与D2之差即为瓷砖胶的竖向回弹变形量。瓷砖胶的回弹量属于材料本身特性参数，与布料管数无关。

调平瓷砖所施加的外力(竖向力)等于瓷砖胶的反弹力与瓷砖重力之差。在初始时刻，瓷砖胶的反弹力为0 N，瓷砖竖向力等于瓷砖重力(150 N)，此时瓷砖受拉；在调平过程中，随着瓷砖竖向位移增加，瓷砖胶压缩变形逐渐增大，反弹力相应提高，瓷砖开始受压；当瓷砖竖向位移下压至Ds时，瓷砖胶条之间开始接触，瓷砖胶的压缩变形受限，反弹力急剧增大；当瓷砖胶间隙接近0 mm时，反弹力达到最大，此时，瓷砖竖向压力达到最大值Pm。由图5可知，布料管数越多，瓷砖胶条的间距越小；这意味着在压缩变形过程中，瓷砖胶条之间越早接触。因此，瓷砖压力急剧增长的时间点Ts随布料管数增加而明显提前。瓷砖胶的最大反弹力源于其自身的弹性变形，与布料管数无关，所以，瓷砖的Pm几乎不受布料管数影响。

3.2.2 接触面积

不同布料管数时瓷砖胶与瓷砖的接触面积S1及其与基层的接触面积S2随时间的变化如图9所示。在直压加载过程中，不同布料管数的接触面积S1均从0 m2逐渐增大至约0.64 m2，卸载后S1瞬间降低至0 m2而后迅速恢复至0.29 m2左右；接触面积S2从不同的初始值逐渐增大至约0.64 m2，卸载后S2急剧下降随后恢复至0.63 m2左右。

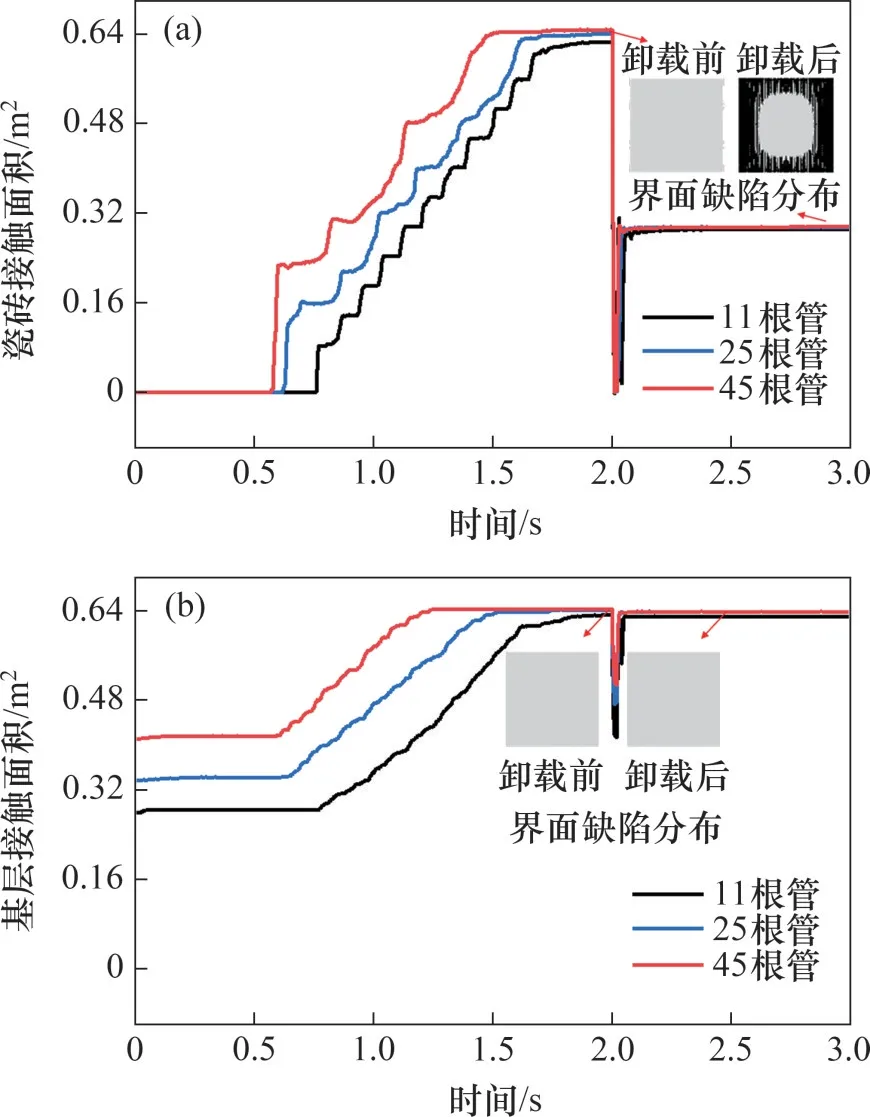
图9 瓷砖胶与瓷砖和基层的接触面积随时间的变化Fig.9 Variations of the tile-adhesive contact area and adhesive-concrete base contact area with time

接触面积的变化主要取决于瓷砖胶的初始形态以及直压过程中的变形情况。在初始时刻，瓷砖未与瓷砖胶接触，接触面积S1为0 m2；布料管数越多，瓷砖胶条的间距越小，则接触面积S2越大；在加载过程中，瓷砖胶变形逐渐增大，接触面积随之增加直至瓷砖胶条间隙接近0 mm，满浆率几乎达到100%；卸载后瓷砖胶回弹导致其与瓷砖完全脱离，接触面积S1降为0 m2，S2急剧下降；瓷砖在重力作用下回落后接触面积回升并保持稳定。由于回落量小于回弹量，接触面积S1的稳定值远小于其最大值；而回弹变形主要发生在变形受限的顶部瓷砖胶(如图8(a)所示)，底部瓷砖胶的回弹变形较小，因此，接触面积S2的稳定值与其最大值较接近。

此外，瓷砖胶的最终变形情况由材料的应力应变特性所决定，与布料管数无关。因此，最终的接触面积S1和S2几乎均不受布料管数的影响。

图10所示为布料管数分别为11、25和45根时瓷砖-瓷砖胶界面缺陷的分布云图。由图10可知，瓷砖与瓷砖胶的脱空缺陷主要集中在瓷砖边缘处，平行于布料方向。这主要是由于在直压作用下瓷砖胶在约束较低的边缘处产生了较大的塑性变形，外力卸载后瓷砖胶无法恢复形变导致在边缘处出现了明显的脱空。此外，尽管缺陷面积(对应接触面积)与布料管数无关，但是随着布料管数的增加，瓷砖胶条间隙缩短引起脱空条纹明显变窄且分布更加均匀，这有利于延缓硬化后瓷砖空鼓的进一步发展[22-23]。

图10 不同布料管数时瓷砖-瓷砖胶界面缺陷的分布云图Fig.10 Contour plots of the distribution of tile-adhesive interfacial defect under various rows of adhesive extrusion

3.3 荷载类型的影响(水平布料，管数为45根)

3.3.1 直压-垂直振动荷载(VC-VV模式)

图11(a)所示为VC-VV加载模式下瓷砖竖向位移和竖向力随时间的变化。在前2 s的直压过程中瓷砖竖向力与位移的变化规律与图8中的一致，达到目标位移D1(5.245 mm)时竖向力达到最大值Pm(3.40 kN)；之后施加垂直振动荷载，竖向位移以0.025 mm的幅值波动，竖向力与之同步呈波动变化，在位移向下时达到最高，向上时降至最低；随着作用时间的增加，竖向力的最大值和最小值均不断减小。卸载后，竖向位移轻微波动，随后保持稳定位移D2(5.142 mm)；竖向力由1.66 kN降至0 kN。

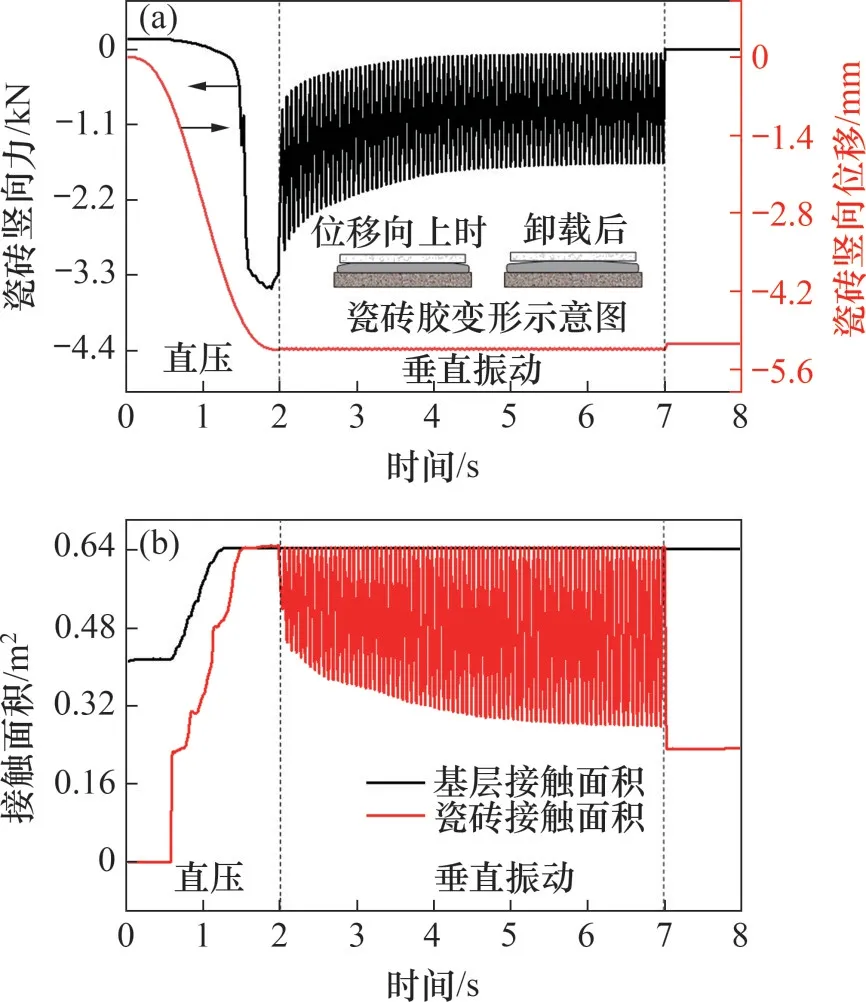
图11 直压-垂直振动时瓷砖竖向位移和竖向力以及接触面积随时间的变化Fig.11 Variations of vertical displacement and force of tile and contact areas with time when loading the vertical vibration with compression

如前所述，调平瓷砖所施加的外力(竖向力)与瓷砖胶的反弹力即瓷砖胶的弹性变形呈正相关。下压时，弹性变形增加，反弹力增大；上移时，恢复部分弹性变形，反弹力降低。新拌瓷砖胶作为一种典型的水泥基材料，在动荷载下呈现显著的黏弹塑性[24-25]，即随着振动加载时间的增加，瓷砖胶的塑性变形增加，弹性变形占比减小，瓷砖反弹力逐渐降低。外力卸载后，瓷砖胶的弹性变形完全恢复，仅残留塑性变形，D1与D2之差(0.103 mm)即为瓷砖胶的竖向回弹变形量。

在直压-垂直振动耦合荷载作用下瓷砖胶与瓷砖接触面积S1以及瓷砖胶与基层接触面积S2的演化过程如图11(b)所示。从图11(b)可以看出，接触面积S1和S2均在直压作用下达到0.640 m2；施加垂直振动荷载后，接触面积S2保持稳定，S1与竖向位移同步呈波动变化，在瓷砖下压时达到最高，上移时降至最低；随着作用时间的增加，S1的波峰保持为0.640 m2，波谷不断减小；卸载后，S1降至0.232 m2，S2保持为0.640 m2。

接触面积S1的变化主要源于垂直振动过程中瓷砖胶的不均匀变形。具体来讲，当瓷砖下压至0.025 mm时，瓷砖胶压缩变形增大，接触面积S1随之增加；瓷砖上移0.025 mm时，部分弹性变形恢复，瓷砖与瓷砖胶的接触面积相应减小。随着振动加载时间的增加，瓷砖胶的塑性变形增大，尤其在约束较低的边缘处产生较大的塑性变形，致使瓷砖胶呈现中心饱满、边缘塌陷的状态(图11(a))，从而导致上移时与瓷砖的接触面积降低；外力卸载后，中心瓷砖胶的弹性变形完全恢复，瓷砖胶在中心与边缘的不均匀变形加剧(图11(a))，最终导致接触面积S1明显降低。

此外，由3.2.2节可知，与顶部瓷砖胶相比，底部瓷砖胶的回弹变形较小，对接触面积S2影响较小。垂直振动加载和卸载后，底部瓷砖胶的塑性变形增大，回弹变形的影响进一步减小。因此，瓷砖胶与基层的接触面积S2在加载过程中以及卸载后始终保持不变。

3.3.2 直压-剪切振动荷载(VC-SV模式)

在VC-SV加载模式下瓷砖竖向位移、竖向力以及接触面积随时间的变化如图12所示。显然，在施加剪切振动荷载后，竖向位移保持不变；竖向压力逐渐减小，在5.52 s时压力转变为拉力逐渐增大直至保持稳定。卸载后，竖向位移保持稳定，无回弹；竖向力由45 N瞬间降至0 N。接触面积S1和S2在剪切振动作用时和卸载后基本保持为0.640 m2。

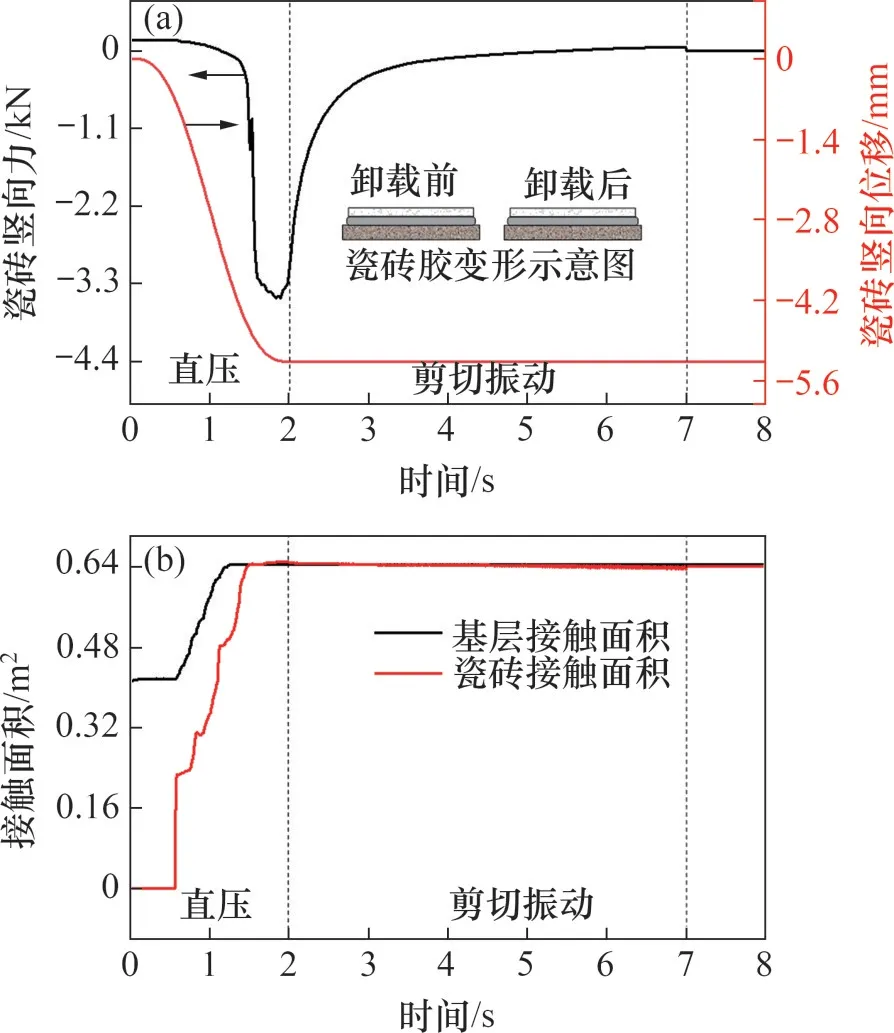
图12 直压-剪切振动时瓷砖竖向位移和竖向力以及接触面积随时间的变化Fig.12 Variations of vertical displacement and force of tile and contact areas with time when loading the shear vibration with compression

上述现象表明，瓷砖胶在剪切振动作用下主要发生塑性变形，弹性变形占比随着加载时间的延长逐渐降低、反弹力下降，导致瓷砖竖向力相应减小；当瓷砖胶的反弹力不足以抵抗瓷砖重力时，瓷砖竖向力由压力转变为拉力。卸载后瓷砖胶在瓷砖重力作用下难以发生屈服变形，瓷砖竖向位移基本保持不变。此外，由于在剪切振动加载和卸载后，瓷砖胶始终发生均匀变形，因此，接触面积S1和S2始终保持不变。

3.3.3 不同加载模式对比

不同类型荷载作用时瓷砖的铺贴质量如图13所示。从图13可见：相较于单一的直压荷载，耦合垂直振动后，瓷砖回弹量降低了37.58%，接触面积S1减小了21.62%，接触面积S2增大0.31%；耦合剪切振动导致瓷砖回弹完全消失，接触面积S1增大了116.22%，接触面积S2增大0.31%。这表明，振动荷载的引入可以有效地减小瓷砖胶弹性变形的影响，从而降低瓷砖回弹量，有利于增加瓷砖的初始平顺性；然而，垂直振动荷载会同时引发瓷砖胶的不均匀变形，进而降低瓷砖胶与瓷砖的接触面积S1。VC-SV模式下接触面积S1显著增大，其主要是因为剪切振动过程中瓷砖胶仅发生均匀的塑性变形且卸载后竖向弹性变形为零。

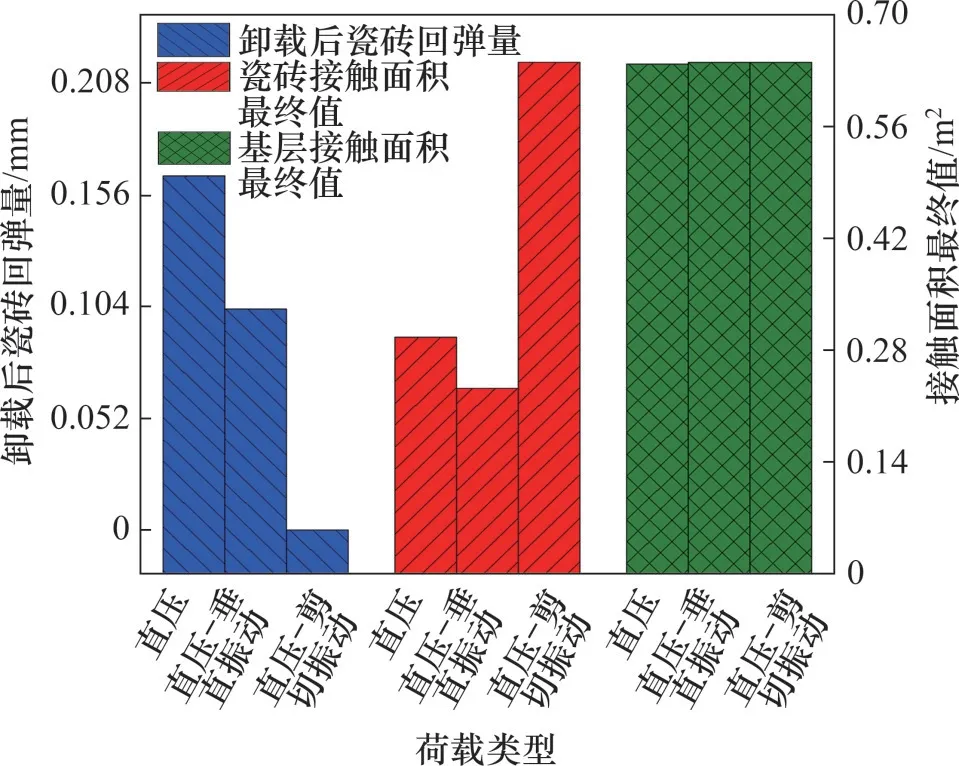
图13 不同类型荷载作用时瓷砖的铺贴质量Fig.13 Installation quality of ceramic tiles under the actions of various loads

图14所示为不同加载模式对瓷砖-瓷砖胶界面缺陷分布的影响。从图14可见：与单一直压荷载作用下的脱空条纹不同，耦合垂直振动荷载后，瓷砖胶的不均匀变形不仅增大了脱空面积，而且脱空区域主要集中分布在瓷砖四周。这些大尺寸铺贴缺陷的存在将显著加速硬化后瓷砖空鼓的进一步发展。而耦合剪切振动后，瓷砖基本满浆，仅出现少量均匀分布的极细脱空条纹，铺贴质量最优。