基于矩形波导阻抗变换器的设计与仿真

黄 勇,赵 腾,王秀芳

(西南交通大学 物理科学与技术学院,四川 成都 610000)

在微波电路中,不同传输线、不同元件以及各种天线与馈线之间的连接都存在阻抗匹配问题.若直接连接两特性阻抗不同的微波元件或传输线,则会产生反射,影响系统的信号传输.而当在两微波元件之间连接一段或多段特定阻抗、特定长度的匹配网络后,可使其阻抗匹配,则接入的匹配网络就称之为阻抗变换器.

阻抗变换器是一种两端口微波元件,在微波系统中引入阻抗变换器,可消除系统因特性阻抗不匹配而产生的反射. 为了适应不同的应用场合,研究者设计研究了不同类型的阻抗变换器.如文献[1-3]设计研究了T形、∏形和P型双波段阻抗变换器,主要应用在多波段工作系统中. 根据微波电路中的宽带要求,官伯然等人[4]设计实现了一款超短波宽带阻抗变换器.另外,如非常规变比阻抗变换器[5]、低频天线阻抗变换器[6]和复数负载阻抗变换器[7]也相继出现,为进一步满足了特定场景对阻抗变换器的需求提供了一定的研究基础.

目前应用较多的阻抗匹配元件有以下3种:四分之一波长阻抗变换器、二项式阻抗变换器和切比雪夫阻抗变换器.李艳芳等人[8]分析了四分之一波长阻抗变换器的原理,但是四分之一波长阻抗变换器工作频带很窄;当工作频率偏离中心频点时,匹配性能急剧下降. 切比雪夫阻抗变换器[9,10]也得到广泛关注,如周越等人[9]对切比雪夫阻抗变换器的设计方法进行了研究,讨论了2种不同策略方法的设计步骤.通过上述文献发现,研究者针对单一阻抗变换器研究较多,而同时对2种或2种以上的阻抗变换器的研究较少.但是,在实际的工程问题上,针对给定的元件间的阻抗匹配,应该选用什么样的匹配元件是一个重要的课题.

针对上述问题,本文以一个待匹配的端口为BJ70接口,其尺寸为窄边b0=15.799 mm,宽边a0=34.849 mm;另一待匹配端口为已调试好的5.8 GHz矩形波导定向耦合器的接口,其尺寸为窄边b2=16.28 mm,宽边a2=38.19 mm为例,研究了上述3种匹配元件的适用情况.定向耦合器S参数[11]的数值如图1所示.图中S11表示输入反射系数;S31的负值数值上等于耦合度C;差值(S31-S41)数值上等于方向性系数D.

图1 波导各端口S参数与频率关系曲线

本文将首先介绍3种阻抗变换器的工作原理及设计方法,这3种阻抗变换器分别为四分之一波长阻抗变换器、二项式阻抗变换器和切比雪夫阻抗变换器;接下来,我们将在本文所提到的设计指标下,对三者进行仿真设计;最后进行对比分析.

1 三种阶梯式阻抗变换器设计原理

1.1 四分之一波长阻抗变换器

四分之一波长阻抗变换器是最简单的单段式阻抗匹配器.值得指出的是这里提到的“波长”指的是波导波长λg,而匹配段的长度即为l=λg/4. 若设a表示波导宽边长度,而b表示波导窄边长度,则波导波长λg与工作波长λ之间的关系为

(1)

(2)

其中μ、ε分别为真空磁导率与真空介电常数. 三段特性阻抗之间的关系[13]:

(3)

其中Z1为阻抗变换器等效阻抗,Z0为BJ70端口阻抗,Z2为定向耦合器等效阻抗. 不妨令阻抗变换器窄边b1与另外两段窄边有如下关系:

(4)

通过联立式(2)—(4)可得阻抗变换器长边a1.

1.2 二项式阻抗变换器

二项式阻抗匹配器与下面会提到的切比雪夫阻抗变换器都是多段阻抗变换器.区别在于它们每一段阻抗的大小排布不同[14].

(5)

总反射系数为

(6)

其中,定义电长度

(7)

而2(i-1)为电磁波从某端口进入,再从此端口反射出时经历的匹配段总段数. 若将任意反射系数写为

Γi=kiΓ1

(8)

则式(6)可改写为

(9)

由于

(10)

|Γ|=Γ1|cosnθ|

(11)

Γ1|cosnθ|函数的特点如图2所示,在某Γm下,随着n的增大,曲线愈加平缓,所以二项式响应又叫“最平坦响应”.

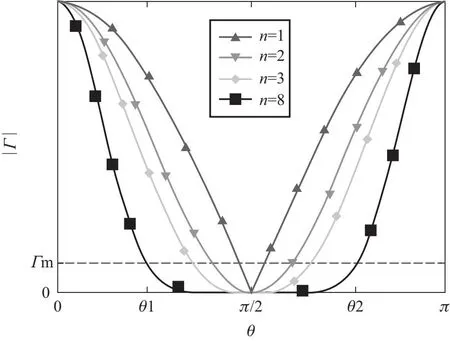
图2 |Γ|在不同n值下随θ变化关系

(12)

(13)

进而得

(14)

又由式(8)和(12)联立有

(15)

只要n已知,就可以将式(14)、(15)联立即可求得各段特性阻抗.

下面将求解n. 设Γm是设计允许的最大反射系数,λ1、λ2是Γm对应的两波长,其间的频率范围即为带宽,其对应的电长度为θ1、θ2. 由式(11)得

Γm=Γ1|cosnθ1|=Γ1|cosnθ2|

(16)

求解式(16)方程即可求得n.

1.3 切比雪夫阻抗变换器

设反射系数Γ1=Γn+1,Γ2=Γn,使之左右对称. 紧接着1.2节中式(6),得

e-j2(n-1)θ+Γn+1e-j2nθ=e-jnθ(Γ1ejnθ+Γ2ej(n-2)θ+…+Γne-j(n-2)θ+Γn+1e-jnθ)

(17a)

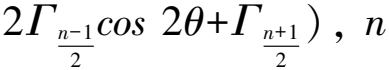
(17b)

这里的每一项cosnθ项均可展开为关于cosθ的多项式,如

cosθ=cosθ,cos 2θ=2 cos2θ-1,

cos 3θ=4cos3θ-3cosθ,

cos 4θ=8cos4θ-8cos2θ+1

(18)

令x=cosθ,Tn(x)=cosnθ=cos (narccosx),代入上式得

T0(x)=1,T1(x)=x,T2(x)=2x2-1,…

(19)

Tn(x)是为切比雪夫多项式. 其递推公式为

Tn+1(x) = 2xTn(x)-Tn-1(x)

(20)

(21)

其图像如图3所示,可以观察得到,在|x|≤1时其图像为一系列最大值不大于1的波纹;当|x|>1时图像急剧上升.

图3 在不同n值下切比雪夫多项式|Tn(x)|

(22)

其图像如图4所示.

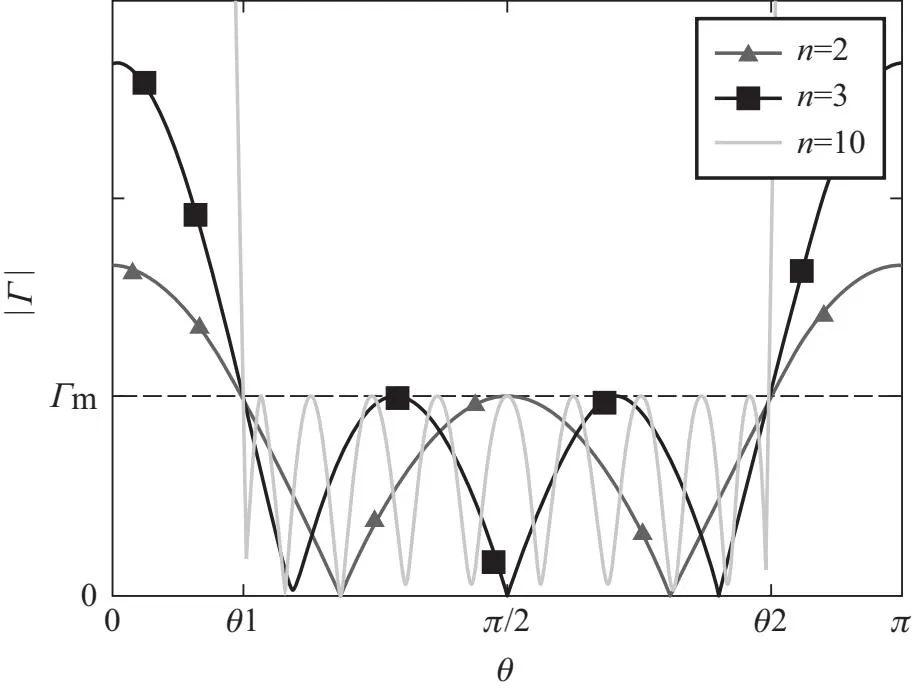
图4 |Γ|在不同n值下随θ变化关系

可以看到|Γ|在θ1、θ2范围内始终不超过Γm.因此为保证|Γ|有如上所述的分布,我们只需要将式(17)取模后根据式(18)展开成关于cosθ的多项式,整理后让各项系数与式(22)的各项系数一一对应相等即可求出各Γi的值,又由式(8)得到各ki的值,代入到式(14)和(15)即可求得各段特性阻抗的值.

2 三种阻抗变换器的仿真设计

综合上述分析,根据多段二项式阻抗匹配段的最平坦特性,我们基本可以从理论上得出多段二项式阻抗变换段设计的S11参数会比四分之一波长阻抗变换器更低的结论.同时,又由于两待匹配段的尺寸很接近,还可以从理论上得出切比雪夫阻抗变换器S11参数的特征会一定程度上趋于二项式阻抗匹配段S11参数特征的结论,而此分析会在本文3.1节的第二个问题中做具体讨论.为验证上述理论分析结果,同时观察其它S参数的情况,本文采用有限元方法仿真设计了三种阻抗变换器.

2.1 四分之一波长阻抗变换器的仿真设计

由式(2)—(4)可求得

经仿真并进行参数优化后各S参数如图5所示.

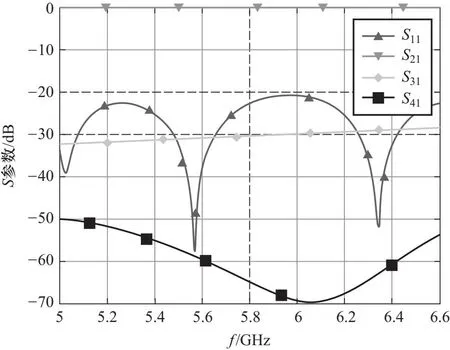
图5 匹配阻抗变换器的定向耦合器各端口S参数

中心频率处各参数指标如上表1所示,均满足设计要求.

表1 中心频率处阻抗变换器仿真结果

2.2 二项式阻抗变换器的仿真设计

由于2.1节中,四分之一波长阻抗变换器S11参数已经满足了设计指标要求.因此为了体现明显区别,我们不妨直接设计一个n=3的二项式阻抗变换器.

(23)

经仿真并进行参数优化后各S参数如图6所示. 中心频率处各参数指标如表2所示,均满足设计要求,且S11大大降低.

表2 中心频率处二项式阻抗变换器仿真结果

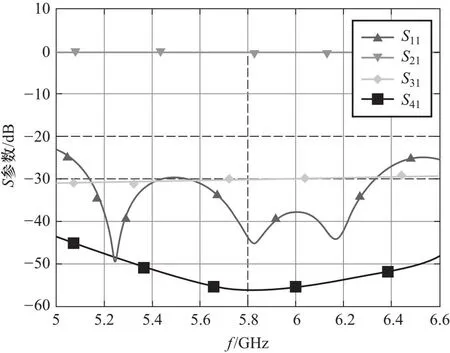
图6 匹配二项式阻抗变换器的定向耦合器各端口S参数

2.3 切比雪夫阻抗变换器的仿真设计

为与2.2节中的二项式阻抗变换器做一个对比,我们同样令n=3,代入1.3节计算得

k1:k2:k3:k4=1:3(1-cos2θ1):3(1-cos2θ1):1

k1:k2:k3:k4=1: 2.055: 2.055: 1,

(24)

经仿真并进行参数优化后各S参数如图7. 中心频率处各参数指标如表3所示,其S11虽然有一定的改善,但方向性下降,频带宽也完全不满足设计要求.

表3 中心频率处切比雪夫阻抗变换器仿真结果

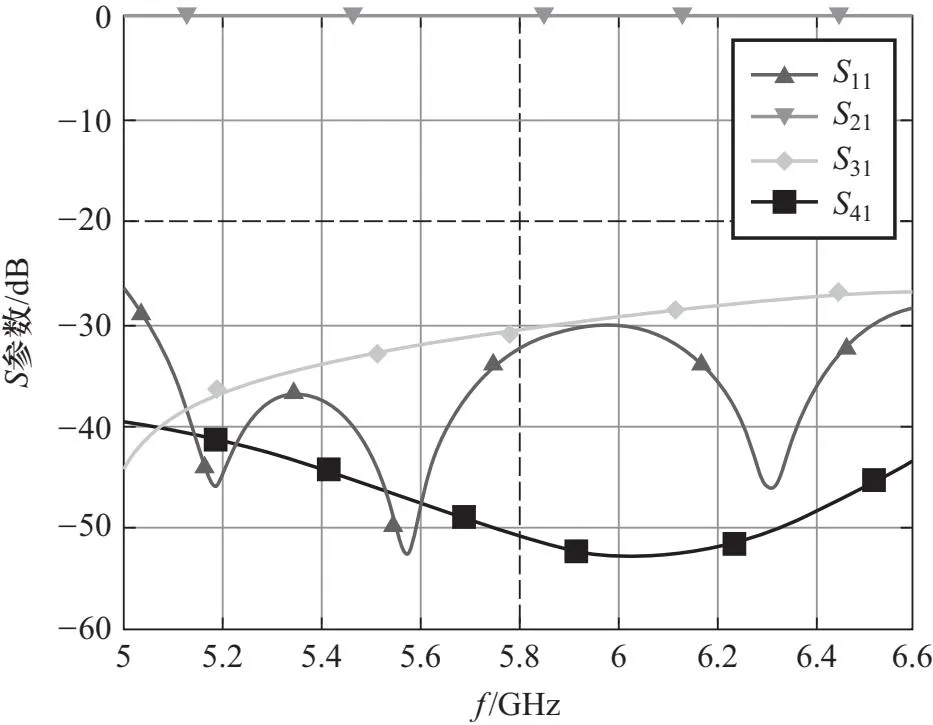
图7 匹配切比雪夫阻抗变换器的定向耦合器各端口S参数

3 仿真结果的讨论

3.1 问题讨论

首先,讨论第1个问题:为什么2.1节中图6的S11似乎并没体现出二项式阻抗变换器的最平坦分布?这是因为在设计阻抗匹配段时,只考虑了某一端口Z0到Zn+1的一系列阻抗匹配,并没有考虑定向耦合器内部如小孔和其他端口的反射系数.如果去掉小孔和其他端口进行仿真,其S11图像如图8所示. 在±0.4 GHz范围内是很符合最平坦特征的.切比雪夫也同理,如图9,其基本符合图4中n=3时中间有一个峰值,两边有两个极小值的分布特点.

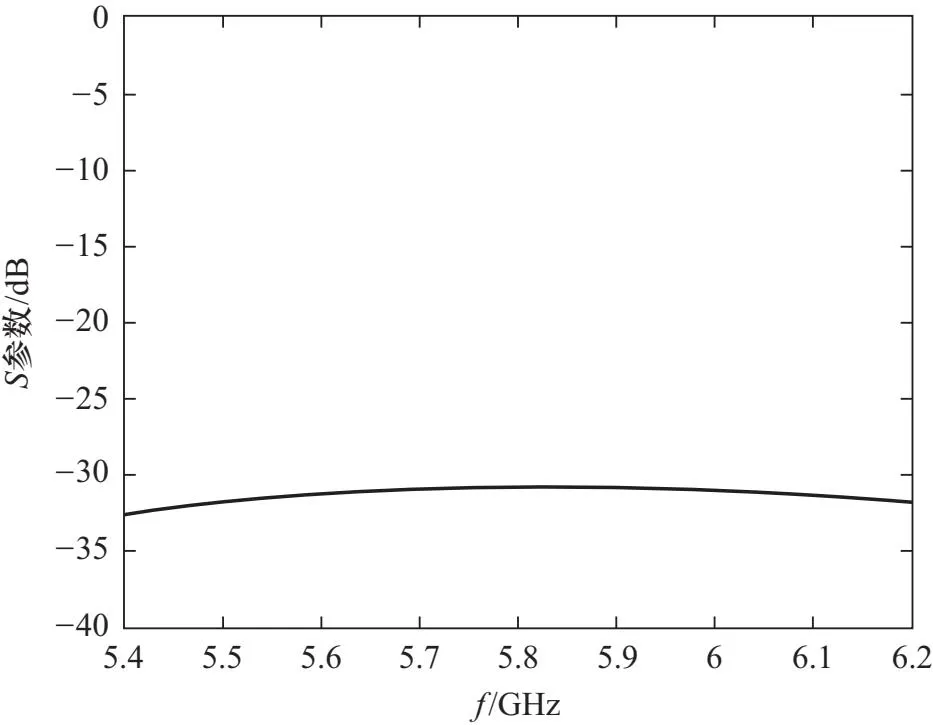
图8 去掉小孔和其他端口后的S11与频率关系曲线

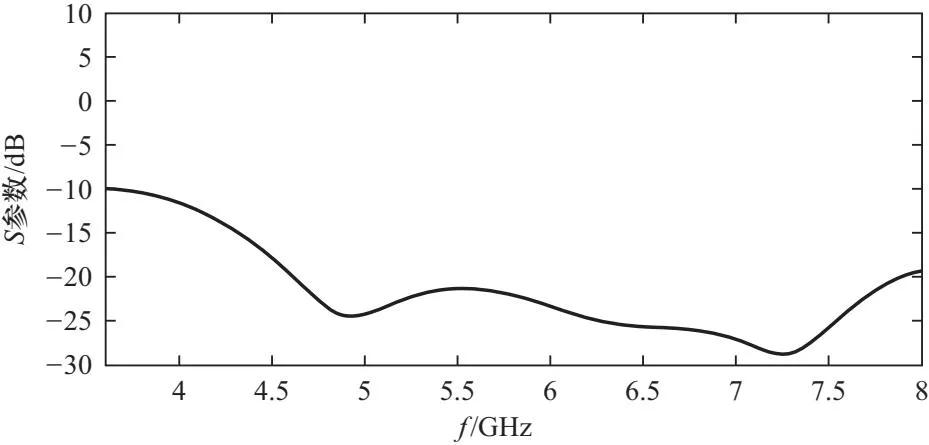
图9 去掉小孔和其他端口后的S11与频率关系曲线

第2个问题: 为什么本次仿真的切比雪夫阻抗变换器有一定的二项式阻抗变换器的特征?如图9所示,其S11接近“U”型的分布与图2中二项式阻抗变换器反射系数的分布有一定程度的相似.这是因为BJ70接口与我们需要匹配的定向耦合器的接口特性阻抗相差不大.这就造成了式(23)和(24)中计算出的二项式和切比雪夫各阻抗匹配段特性阻抗相差很小,进而也就造成了这种相似性.

表4 取不同n值时两种设计方法各ki比值情况

3.2 三种设计的综合比较

中心频率处三种设计的各S参数如表5所示. 综合比较表5数据,可以得到如下一些结论:

表5 三种设计方案中心频率处仿真结果对比

2) 若要追求最小的驻波比,则推荐采用三阶二项式设计. 通过文献[16]也可说明采用二项式所设计的阻抗变换器,其驻波比最小.

3) 综合评估我们所要设计定向耦合器的各项指标要求及应用场合,不建议采用切比雪夫设计,首先其方向性的变差导致其频带宽变得很窄;且又因为BJ70波阻抗与需要匹配的端口波阻抗过于接近,我们从理论上就已能得出切比雪夫设计的特点无法很好体现,而在进一步参数优化过程中,各项参数也会趋于三阶二项式设计的参数,导致退变为二项式阻抗变换器.

4) 为了验证本文的仿真设计的有效性,对已有文献进行了对比,如表6所示. 可发现所设计的阻抗变换器其反射系数较优于其他文献.

表6 其他文献结果对比

4 结论

本文介绍了3种阶梯式阻抗变换器的相关计算推导,并设计了针对BJ70接口的三种阻抗变换器,最后对其进行了仿真验证.通过比较计算分析和仿真验证后的结果,我们不建议采用切比雪夫的设计;而若在设计指标之下还要要求更好的驻波比,则推荐采用二项式的设计;不过综合而言,我们更推荐四分之一波长阻抗变换器的设计,因为其展现出更好的带宽和方向性,以及尽量小的波导尺寸.此外对计算和仿真结果的进一步分析,我们也发现,在两待匹配端口阻抗相接近和设计指标要求的频带宽较时,都不推荐采用切比雪夫阻抗变换器设计.