基于傅里叶变换的不确定性原理

于海燕,郑神州

(1. 内蒙古民族大学 数学科学学院,内蒙古 通辽 028043;2. 北京交通大学 数学与统计学院,北京 100044)

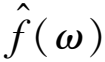
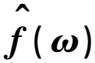
表1 可积函数f(x)与其傅里叶变换之间的关系

量子力学与经典物理学的不同之处在于:物体同时具有粒子和波的双重特性(波粒二象性),作为描述量子态规律的薛定谔方程的解是用复变函数形式表示,从统计学的角度看, 量子场解的模平方表示量子运动的概率密度函数. 系统的能量、动量和其他量可以保持为测量值(量子化),并且得知测量值的精度有限(不确定性原理);与经典力学比较最显著的一个差异,就是不确定性原理. 在量子力学当中,粒子的位置越精确,它的动量就越难确定,反之亦然[4]. 事实上,量子不确定性背后是否有更深刻的原理,这是美国《科学》期刊列出的新世纪要解决的125个科学前沿问题中的第21个,故其研究的重要性不言而喻.

对于信号传播与其傅里叶变换传播之间的一个更为定量的表述是量子力学中最著名的不等式:海森伯不确定性原理. 傅里叶变换的伸缩属性可以看作:如果我们挤压x中的函数,则其傅里叶变换在ξ中伸展,即同时集中任意一个函数和它的傅里叶变换是不可能实现的.实际上,Paley-Wiener定理:如果f(x)是紧支撑的一个非零分布(这包含紧支撑函数),则其傅里叶变换从不拥有紧支撑; 直接蕴涵在调和分析下的测不准原理的一个非常初等的形式[3,4].

1 傅里叶变换、逆变换式及基本性质

傅里叶变换定义为[1,2]:设

则其傅里叶逆变换式

我们先列出几个有用的基本性质:

1) 线性性质: 若

如果α,β是常数,则有

F[αf1(t)+βf2(t)]=αF[f1(t)]+βF[f2(t)]

2) 位移和伸缩变换性质:

F[f(t±t0)]=e±iωt0F[f(t)],

3) 微分性质:若f(x)在(-∞, +∞)上连续或仅有限个可去间断点,且当|x|→+∞时,f(x)→0, 则F[f′(x)]=iωF[f(x)].

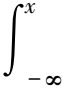
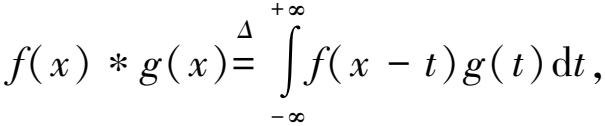
6) Plancherel恒等式:设f∈L1(n)∩L2(n),那么n), 且

2 海森伯不确定性

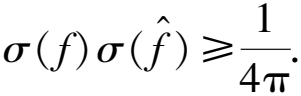
下面我们依据第一节中的傅里叶变换性质,给出海森伯不确定性原理的一个证明.

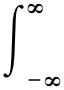
(1)

上面最后一步用了微分性质3.利用Plancherel恒等式和Cauchy-Schwarz不等式, 得到

(2)

另一方面,我们知道任何复数的模总是不少于它的实部.于是有

(3)

所以

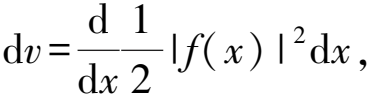
注记1:海森伯不确定性原理不仅对复值函数成立, 通过类似方法可以验证海森伯不确定性原理适用于更一般的标准线性变换、小波变换和更一般的微分-积分变换,最近研究的成果将其拓广到了Clifford代数中的四元数值等问题上相应的各种变换[5-7].

3 Hardy(哈代)不确定性原理

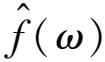
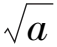
(4)

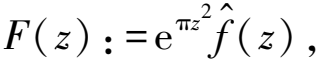
2) 下面的菲拉格曼-林德洛夫原理,实际上它是解析函数最大模原理在无界区域上的一个推广.严格地说,我们不能直接利用一般形式的菲拉格曼-林德洛夫原理,因为它需要函数F(z)是一次幂的指数增长,而在这里有二次幂的指数增长.但是我们可以稍微调整一下F(z)来解决这个问题.首先,设0<θ<π/2,考虑下面的角形区域Γθ:={reiα:r>0,0≤α≤θ},由式(4)可得

|F(ξ+iη)|≤eπξ2

(5)

因此,如果δ>0,并且θ足够接近π/2,则有函数eiδz2F(z)在Γθ的边界上由1控制,那么对于任意足够小ε>0,exp(-iεeiεz2+ε+iδz2)F(z)也在Γθ的边界上由1控制,且在Γθ的内部,在无穷远处趋向于0,从而由极大值原理可知其也由1控制.令ε→0,然后θ→π/2,δ→0,我们可以得到F(z)在右上象限的边界是1,用同样的的方法处理剩下的象限.定理得证.

进一步Hardy不确定性原理可推广为如下.

定理2：设f∈L2(R)满足

|f(x)|≤C(1+|x|)Ne-aπx2,

其中C>0,N∈Z; 那么若ab>1,则f=0;若ab=1,则存在一个阶数至多为N的多项式P(x),使得f(x)=P(x)e-aπx2.

注记2:1) 作为Hardy不确定性在对偶空间(Lp—Lq)上的一个对应,G.W.Morgan[9]得到以下变体版本:设f∈L2(R),10,使得

|f(x)|≤Cexp(-2πp-1ap|x|p),

成立,如ab>|cos(pπ/2)|1/p,那么有f(x)≡0恒成立.

2) Beurling不确定性原理[10]:若f∈L2(Rd),使得

成立,那么存在一个阶数至多为(N—d)/2的多项式P,使得f(x)=P(x)e-π〈Ax,x〉成立,这里A是一个确定的d阶实正定矩阵.