码垛机器人的幂次指数趋近律变结构控制

贾东明，王晓丽，张 昊

（1.河南交通职业技术学院汽车学院，河南 郑州 450000；2.东南大学仪器科学与工程学院，江苏 南京 210000）

1 引言

码垛机器人在物流业中应用非常广泛。它可以将生产线上或物流场站里的各种物料根据需要自动堆成各种剁型，从而方便装卸、存储和搬运等多种物流活动。码垛机器人的出现及使用极大地提高了物流效率，码垛后的剁型适合于叉车操作。特别在一些装卸危险品的场合可以替代工人进行操作，不仅提高了操作效率而且提升了安全性能。目前，我国物流企业使用的机械臂多从外国引进，从而使得物流业的运营成本大幅提高。虽然我国自己已经开始生产制造码垛机器人，并且也在一些物流企业开始应用，但与国外的机器人相比仍旧有一定的差距，特别是在控制精度及智能化程度方面［1-4］。因此我们有必要在机器人控制的算法方面进行深入研究，以期能够解决其在控制精度方面所面临的挑战。

目前，有很多专家学者已经对码垛物流机械臂的控制算法进行了相应的探讨研究。文献［2］对码垛机器人进行了动力学建模，由于使用了平行四边形机构，所以在模型中消除了哥氏转矩和离心转矩，使得运动方程得到简化。文献［3］使用了PID（比例、积分、微分控制）迭代学习算法对码垛机器人进行了控制，并获得了较高的轨迹跟踪精度。文献［4］使用了时间最优化的轨迹控制，得出了满足物理约束的时间最优轨迹跟踪。

为了不失机械臂控制的一般性，在研究时采用二连杆机械臂模型并使用变结构算法进行控制。二连杆机械臂模型由于考虑到了各种因素的影响，可以使得一个非线性、时变、耦合的系统更加一般化，从而提高了算法的实用性。变结构算法在控制机械臂工作方面应用广泛，因为其具有很强的解决非线性控制的能力［5-7］。

2 机械臂数学模型

目前学术界主要采用拉格朗日和牛顿-欧拉两种平衡法来建立机械臂的动力学模型。并且，牛顿-欧拉法比拉格朗日法建立的模型多了摩擦耗能项，其余则完全一样［8］。我们采用二连杆拉格朗日模型，且各参数的具体数值使用参考文献［9］中所使用的数据。本模型在普通码垛机器人模型的基础上增加了哥氏力和离心力，从而使得模型更具一般性。

式中：M（θ）—（2×2）阶正定的质量惯性矩阵；

B(θ，)—（2×2）阶离心力、哥氏力矩阵；

G（θ）—（2×1）阶重力矩阵；

T—（2×1）控制力矩阵；

θ—机械臂各关节的角度值，其一阶、二阶导数分别代表各关节的角速度以及角加速度。

各参数矩阵具体情况如下：

式中：g—重力加速度，其数值是9.8m/s2。

3 基于趋近律的变结构控制研究

滑模变结构算法在应对非线性控制方面作用强大，但其在20世纪50年代提出之初并没有得到应有的关注。由于当时电子技术比较落后，导致其应用受到限制。近几年，电子技术飞速发展，控制器运算速度大幅提升，这一切都为滑模便结构控制算法的应用奠定了基础，此算法开始受到了广泛关注。

滑模面是滑模变结构算法首先要寻找的因素，控制系统运行至此面附近即可被吸引，并沿此面运行至原点。因此，就稳定性而言它是大范围渐进稳定的。

滑模变结构分两个步骤进行系统控制：

（1）从远离滑模面的位置向滑模面靠近的趋近运动。（2）沿着滑模面滑向原点的滑模运动。

3.1 趋近运动的研究

趋近运动是指系统向滑模面s的渐近运动过程。而系统初始或运动过程中，并不一定在滑模面的单侧运行。因此，当系统在滑模面的不同面时应该采用不同的控制率，并在不同控制率的作用下都能朝着滑模面靠近。这也是此算法被称为变结构算法的原因。趋近运动的不同不仅可以使得系统到达滑模面的时间不同，而且可以使得系统达到滑模面的方式不通，所以有很多学者都在致力于趋近律的研究。

等速趋近律：

指数趋近律：

幂次趋近律：

式中：sgns—符号函数，其取值是1或-1，但却依据s的不同而不同。即s＞0时取正值，s＜0时取负值。以上的三种趋近率都保证了s＜0条件的成立，而本条件可以保证系统无论在滑模面上下侧都有能力朝着滑模面上运行。

控制系统使用等速趋近律时，只能被推动到滑模面附近而不能完全到达。然后系统便不断交替穿行于滑模面两侧，从而产生了抖振。

如使用指数趋近律进行控制，则运动方程可描述为：

这样可以看到，系统在离滑模面很远时s(0)e-kt起到了主导作用，因此可以保证系统以较快的速度运动到滑模面附近。当系统靠近滑模面时s(0)e-kt趋于0，而主导作用由-εtsgns占据。这时与等速趋近率原理相同，也无法对抖动进行有效抑制。

如果采用幂次趋近律，其运动方程可展示为：

从而可以看出，此趋近率能促使系统在有限时间内运行至滑模面，且以相切的方式到达滑模面。这样就减少了系统穿过滑模面后进行反向运动的可能，因而从本质上解决了抖振问题。

3.2 滑模运动的研究

上述研究可以得出，趋近率保证了趋近运动在有限时间内到达滑模面。到达滑模面后的滑模运动则是由s函数来保证的，并且保证系统沿着滑模面运动且最终误差为0。滑模面函数如式（10）：

式中：c—可以自由调整的参数；

e—系统误差。

当系统运行到s面时则s=0，带入式（10）之后可以求出：

由式（11）可以看出，随着运行时间的增加，误差就可以趋近于0。而参数c取值的大小与系统误差收敛到0的时间相关，这也为我们c值的选取提供了依据。

3.3 幂次指数趋近律

通过以上的分析可以看到，滑模面在设计之初就以保证误差趋近于0为基础，所以可以不必过多去关注。但不同的趋近率优劣却非常明显，因为趋近率不仅可以决定系统到达滑模面的速度，并且可以决定到达滑模面时的状态，也就是到底是穿过还是切入。所以趋近率应是研究重点。

前面所研究的指数趋近率，虽然能够使得系统快速到达滑模面，但是却没法从根本上解决抖振。幂次趋近率可以解决抖振问题但是其运行到滑模面的时间却不甚理想。虽然也有学者提出可以使用饱和函数替代开关函数来解决抖振问题，但是却只是在一定程度抑制了抖振，并未真正解决问题。而如果能将指数趋近率和幂次趋近率取长补短，则明显可以同时解决趋近时间和抖振问题。因此，可以得出幂次指数趋近律如式：

4 算法的应用

基于幂次指数趋近律的变结构算法可应用于机器人的控制［12-14］。

4.1 控制率的推导

将式（10）求导之后可以得到：

并且由式（1）可以得到：

将式子式（12）～式（14）联立之后能够解出控制率：

二关节位置指令分别是θ1d=cos(πt)，θ2d=sin(πt)。系统的开始状态，即两个机械臂的起始角度值及角速度值分别是

4.2 系统仿真及分析

当系统初始值与目标初始值不同时，控制算法能在很短的时间内使得系统输出跟踪期望输出曲线，如图1、图2所示。控制算法可以使得输出误差在0附近做极小幅波动，对于周期性波动函数的跟踪而言，此算法的控制精度已经很高，如图3、图4 所示。两个关节的相轨迹曲线，可以看出系统能够很快地切入滑模面，且切入之后没有任何振动，如图5、图6所示。因此幂次指数趋近律很好地解决了切入速度与振动的问题，使得滑模变结构算法的控制性能大幅提升。

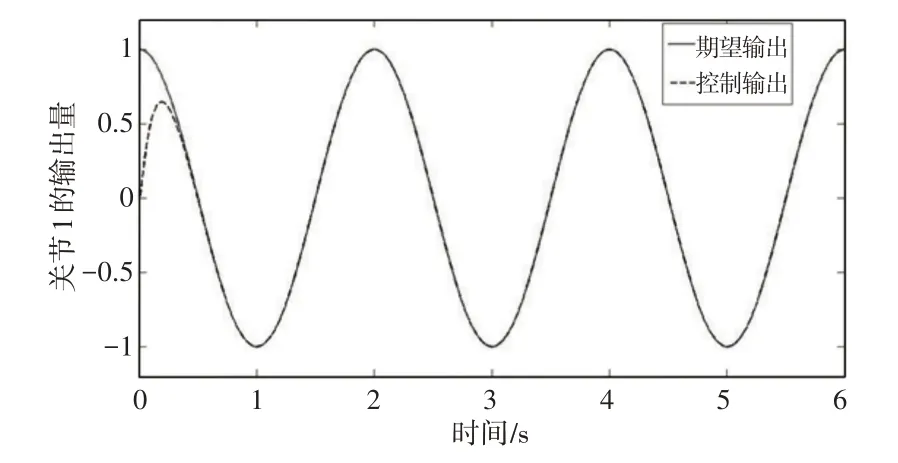
图1 关节1的输出跟踪曲线Fig.1 The Output Tracking Curve of Joint 1

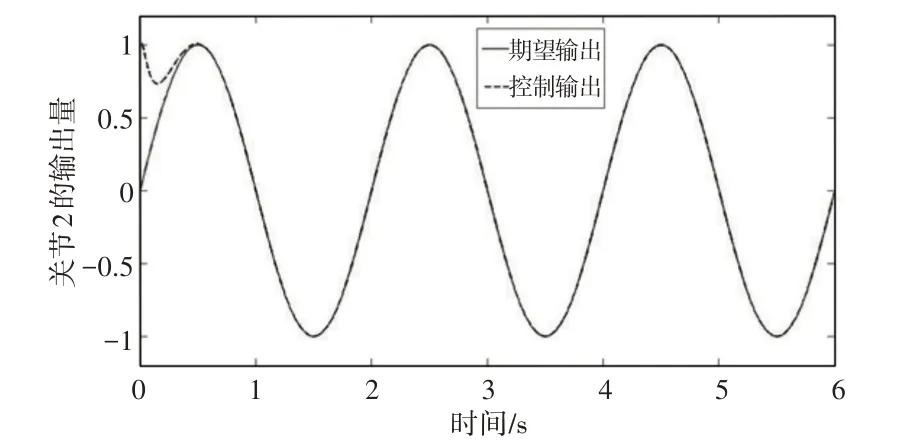
图2 关节2的输出跟踪曲线Fig.2 The Output Tracking Curve of Joint 2

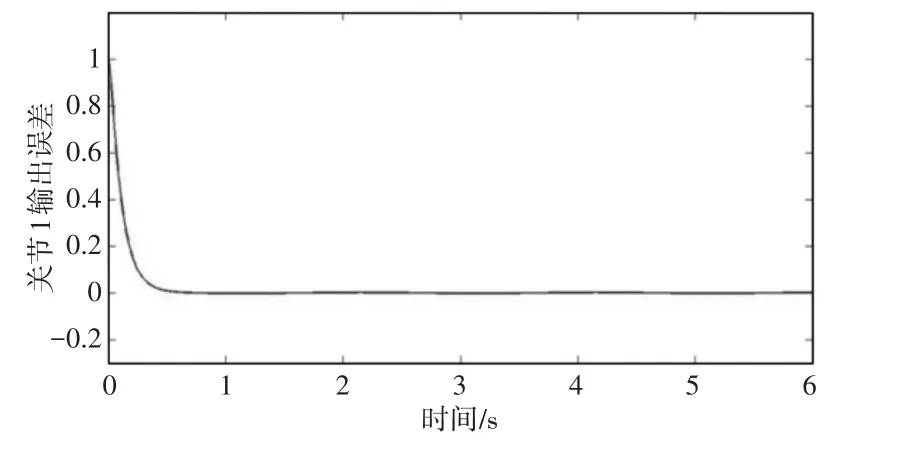
图3 关节1的输出误差曲线Fig.3 The Output Error Curve of Joint 1

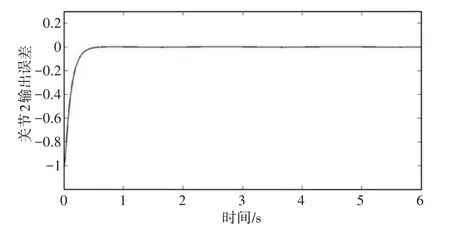
图4 关节2的输出误差曲线Fig.4 The Output Error Curve of Joint 2

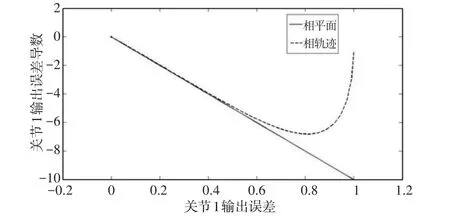
图5 关节1的相轨迹曲线Fig.5 The Phase Trajectory Curve of Joint 1

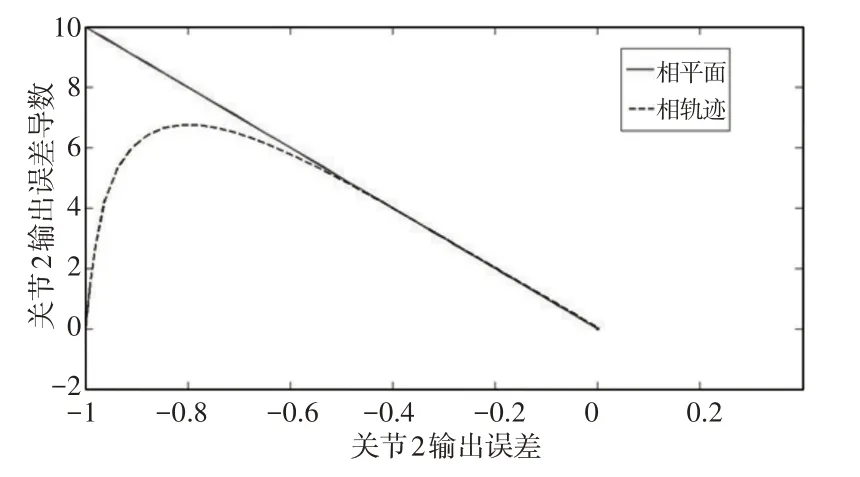
图6 关节2的相轨迹曲线Fig.6 The Phase Trajectory Curve of Joint 2

5 算法的鲁棒性研究

对本函数取导数则可以得出结果小于0，从而能够进一步确认系统稳定的结论。但系统难免会存在外界扰动以及模型参数不准确的情况，而在这种条件下控制器是否具有较强的鲁棒性则是需要进一步讨论研究的。大部分学者都是通过加入扰动来进行研究的，然后通过寻求合适的Lyapunov函数来确认系统鲁棒性。在探索过程中我们很明显可以看出，Lyapunov函数的寻找极具挑战性［8-9］。所以采用求解微分方程的办法而不是使用Ly‐apunov函数来研究系统的鲁棒性。

5.1 基于微分方程求解的鲁棒性分析

滑模变结构算法的控制分远离滑模面的趋近运动和运行至滑模面上的滑模运动。而我们设计的幂次指数趋近律，又将趋近运动分为远离滑模面和靠近滑模面两个步骤。因此需要对这三个阶段分别进行鲁棒性分析。

假设系统建模时存在一定误差，且外界扰动不能被忽略，则（1）可表达为：

式中：ΔM—惯性矩阵；ΔB—哥氏矩阵；ΔG—重力矩阵的建模误差量；ΔT—外界扰动量。

将这四项综合为Δf(x)可表示成：

在控制率设计之初并没有加入Δf(t)的影响，所以控制率还是采用式（15），但这时系统明显已经是式（18）。也就是使用了不考虑扰动的控制率来控制存在扰动的系统，所以将式（15）、式（18）、式（13）联立得：

控制器运动的第一个步骤，从离s面很远向靠近s面运行时，ks起了主要的作用，这时可以求解方程：

得：s=Ce-kt，其中常数C是与起始位置息息相关的，采用常数变异法，将C换成时间t的函数u可以得到：

只要Δf(t)有界，则-M-1Δf(t)有界，设：

其中F是一正常数，则：

式中：C1—与系统起始位置相关的一个常数。

将式（23）代入式（21）得：

由式（24）可以得出，当控制时间逐渐加长，系统就会不断向滑模面靠近，且靠近滑模面的程度是由扰动大小和参数k一起决定的。因此，增加参数k的值在加快系统靠近滑模面速度的同时保证了系统与滑模面靠近的程度。系统运行到滑模面附近则进入了第二个阶段，此时由式（9）可以看出s值处于非常小的状态，而系统运动则受综合扰动影响巨大，即：

t2-t1—积分时间的差值，它的大小与s成正相关，数据越大则离滑模面也越远。但当远离到一定距离后，系统又被迫进入第一阶段。从而能够得出，扰动使得系统往复运行于一、二阶段。第一个阶段可以迫使系统逐渐向滑模面靠近，而第二个阶段却无法保证系统一直处于滑模面附近，好在即使系统远离滑模面也会被随之而来第一阶段趋近率拉回滑模面附近。

系统处于第三个阶段，在没有扰动的情况下是使得系统朝着输出误差和误差导数均趋于零而运动，也即朝着相平面原点运行的状态。但是当存在扰动时，系统只能靠近滑模面而不能完全到达滑模面，所以此时的第三个阶段是需要进行研究的。本阶段由式（10）所决定，所以：

求解微分式（27）可得：

式中：C2—一个积分常数，从式（28）可以得出，误差的第二项最终会趋于0，而第一项才是最终的误差值。

扰动的存在使得误差完全为0变的不可能，哪怕误差是有界的。但好在可以通过增加kc值，来使得输出误差变小。

5.2 加入综合扰动后的仿真

为了对上述的结论进行分析验证，可以将综合扰动加入系统来进行控制。在不改变控制器参数的条件下，给机械臂的两个关节加入相同的扰动量Δf(t)=Asin(πt)。在幅值较小的情况控制效果相当不错，但随着其数值的增大控制效果会逐渐变差。此时选择一个较大的值A=300来获取一个明显的结论。并且从仿真结果来看，第二关节的误差会比第一关节明显增大，因为其累积了第一关节的误差量，所以下面只对第二关节的控制效果进行研究。如图7～图9所示，在控制器参数不变的情况下，其跟踪效果差是由于我们刻意将综合扰动幅值加大而得到的。此时综合扰动的幅值已经大于系统本身的参数变动，所以控制效果变差合情合理。为了验证式（28）结论的正确性，取c=［50 0；0 50］，k=30分别得出结果，如图10～图12所示。能够得到，当参数增大以后输出误差明显变小，在控制初期虽然不能到达s面上，但是最终的控制结果却可以保证输出误差在相平面的稳定点小范围滑动，所以系统的鲁棒性得到了保障。

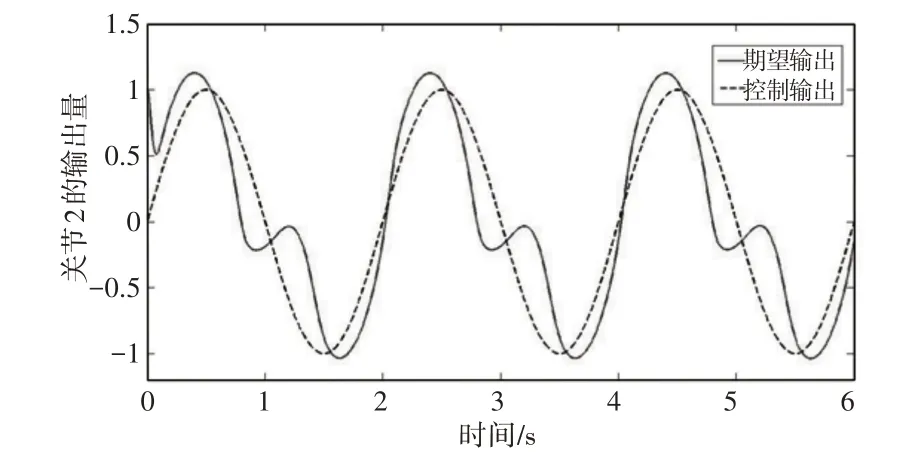
图7 关节2的扰动输出跟踪曲线Fig.7 The Disturbance Output Tracking Curve of Joint 2

图8 关节2的扰动输出误差曲线Fig.8 The Disturbance Output Error Curve of Joint 2

图9 关节2的扰动输出相轨迹曲线Fig.9 The Disturbance Output Phase Trajectory Curve of Joint 2

图10 参数调整后关节2的扰动输出跟踪曲线Fig.10 The Disturbance Output Tracking Curve of Joint 2 After Parameter Adjustment

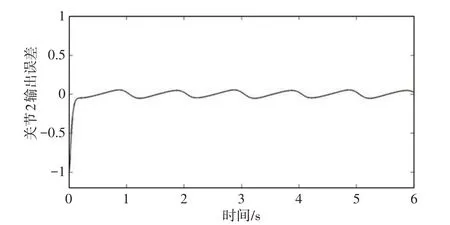
图11 参数调整后关节2的扰动输出误差曲线Fig.11 The Disturbance Output Error Curve of Joint 2 After Parameter Adjustment

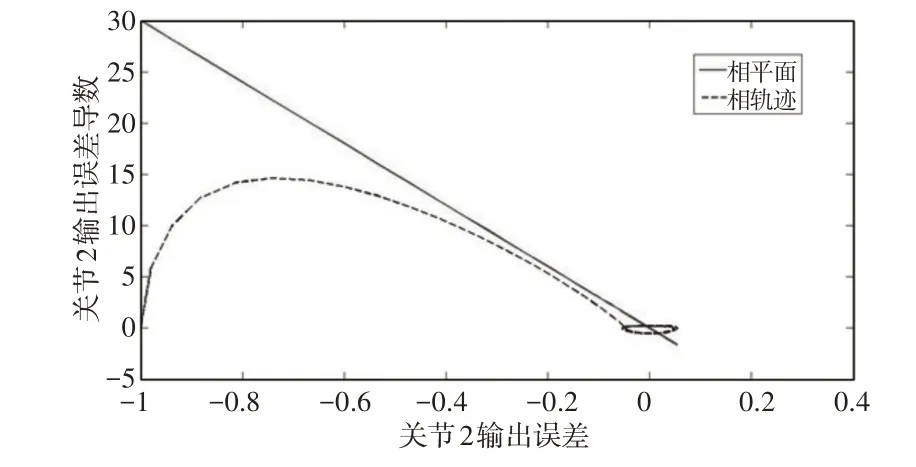
图12 参数调整后关节2的扰动输出相轨迹曲线Fig.12 The Disturbance Output Phase Trajectory Curve of Joint 2 After Parameter Adjustment

6 结语

码垛机器人的广泛应用是物流业、制造业等众多行业高效化生产的基础。而码垛机器人控制中所存在的控制精度低的问题也迫切需要解决。这里所提出基于幂次指数趋近律的滑模变结构控制算法能不仅能有效解决控制精度低的问题，而且保证了控制系统存在建模误差和外界干扰时的鲁棒性。