楔形织构对流体动压润滑性能的影响

崔忠承，乌日开西·艾依提，阿依古丽·喀斯木

（新疆大学机械工程学院，新疆 乌鲁木齐 830047）

1 前言

表面织构作为一种可以有效改善表面摩擦学性能的改性手段，被广泛应用于汽车发动机、轴承密封、人体植入物等领域［1-2］。近年来一些研究表明，当运动方向发生改变时，织构化表面的摩擦性能也随之改变，即摩擦各向异性，织构不同的楔形结构被认为是产生摩擦各项异性的主要原因。文献［3］通过令织构尺寸大于接触面积以消除动压效应进而研究不同形状织构对摩擦各向异性的影响，结果表明表面形状收敛的织构边缘具有较大的局部摩擦响应，而截面形状收敛的织构具有更明显的定向摩擦效应。文献［4-5］对非对称织构的研究表明增大织构形状沿润滑液流动方向的收敛区可以有效增强织构的流体动压效应。而文献［6-7］的研究则表现出了相反的结果。尽管上述研究都观察到织构化表面的定向摩擦效应，但都仅针对表面形状或截面形状进行研究，其结果也不尽相同。为系统研究织构表面形状、截面形状和几何参数对织构动压性能的影响，这里采用基于N-S方程的CFD方法进行数值计算，通过单因素分析研究了流体动压润滑状态下相同工况时织构几何参数对不同楔形结构的织构动压性能的影响，然后通过正交模拟得出了各因素对织构性能影响的主次顺序，为织构的设计优化提供参考。

2 模型建立

2.1 控制方程

考虑惯性项的影响，采用基于N-S 方程的CFD 方法进行计算，计算过程中不考虑温度的变化。因此，润滑液的流动由动量方程和连续性方程控制，分别为：

式中：ρ—润滑液密度；u—沿x、y、z方向的速度矢量u、v、w；p－静压；μ—动力黏度。

2.2 物理模型

织构几何模型示意图，如图1所示。单一织构尺寸相对于摩擦副表面很小，故简化为两个平行的摩擦副。其中，L为织构单元的尺寸，H0为油膜间隙，Hp为织构深度，U为上壁面相对于下壁面的运动速度。其中深度比λ和面积率Sp的定义如下：

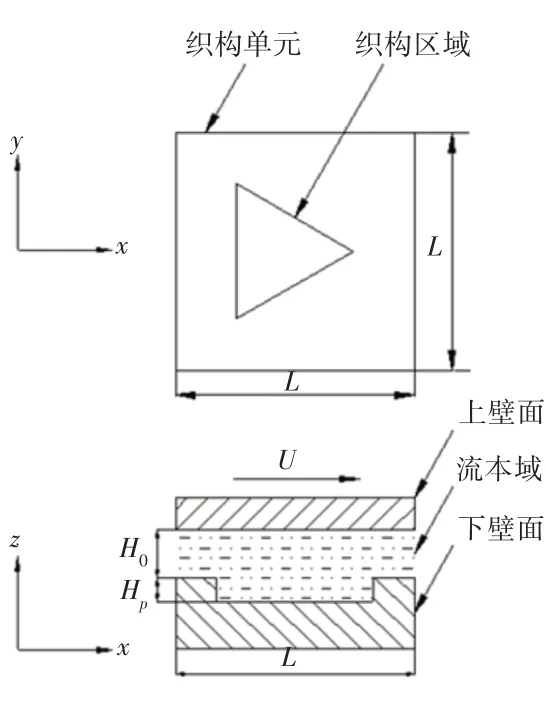
图1 织构几何模型示意图Fig.1 Schematic Diagram of Texture Geometry Model

式中：St—单个织构面积；

S—织构单元面积。

不同类型织构结构示意图，如图2所示。其中，织构表面形状分别为正方形和正三角形。

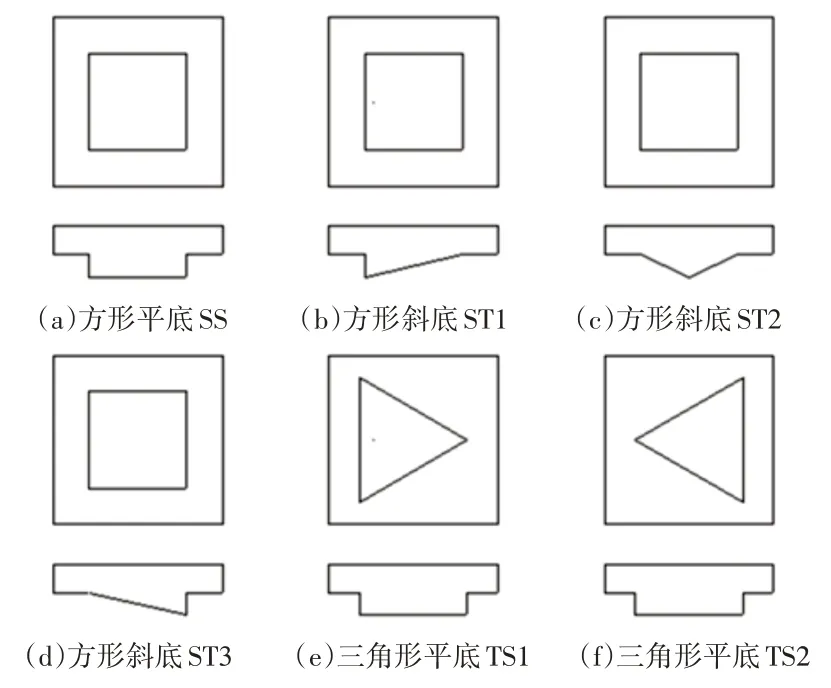
图2 不同类型织构结构示意图Fig.2 Schematic Diagram of Different Types of Texture

2.3 边界条件与网格划分

采用商用CFD 软件Fluent 进行数值计算，流体域上下壁面均为无滑移壁面，上壁面沿x方向以速度U运动，下壁面静止，织构位于下壁面处，在织构单元x、y方向边界处分别引入周期性边界条件以模拟织构阵列中的一个织构单元。为保证工况条件相同，数值模拟中使用的织构具有相同的间隙和运动速度（H0=5μm，U=0.1m/s）。计算采用的流体密度为900kg/m3，动力黏度为0.05Pa·s。由于模型流体域雷诺数较小，因此采用层流模式，CFD模型中的压力项采用二阶中心差分格式，动量项采用二阶迎风格式进行离散，以保证计算精度和稳定性，流体域的求解采用SIMPLEC算法。采用ICEM对流体域进行结构化网格划分，由于网格数量直接影响数值模拟结果的准确性，故进行网格无关性检验，当网格数大于80万时，计算结果趋于稳定。

2.4 织构动压性能评价参数

织构表面作用力是表征织构动压性能的主要参数之一，其中沿z方向的法向力Fz表示承载力的大小，而沿x方向的切向力Fx则表示摩擦力的大小，一般希望获得较高的法向承载力和较低的切向摩擦力，因此引入描述动压性能的参数f，f越大表示织构动压性能越优［8］。其计算方法如下：

式中：p(x，y)—静压分布函数；τ(x,y)—剪应力分布函数。

3 计算结果与讨论

3.1 压力分布

织构上壁面压力分布云图及其上壁面对称轴线处的压力分布曲线图，如图3、图4所示。

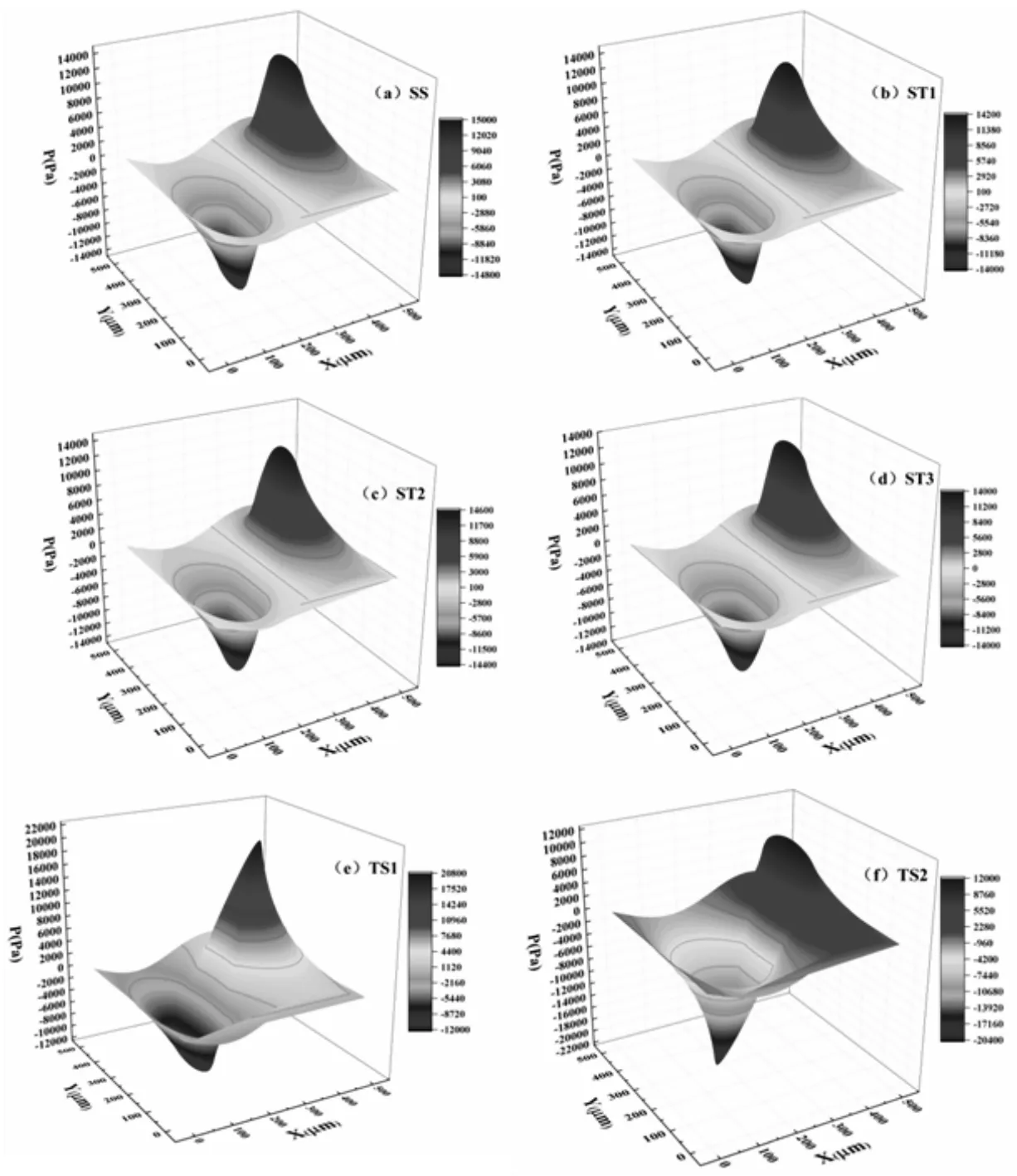
图3 织构上壁面压力分布Fig.3 Pressure Distribution on the Upper Wall of Texture

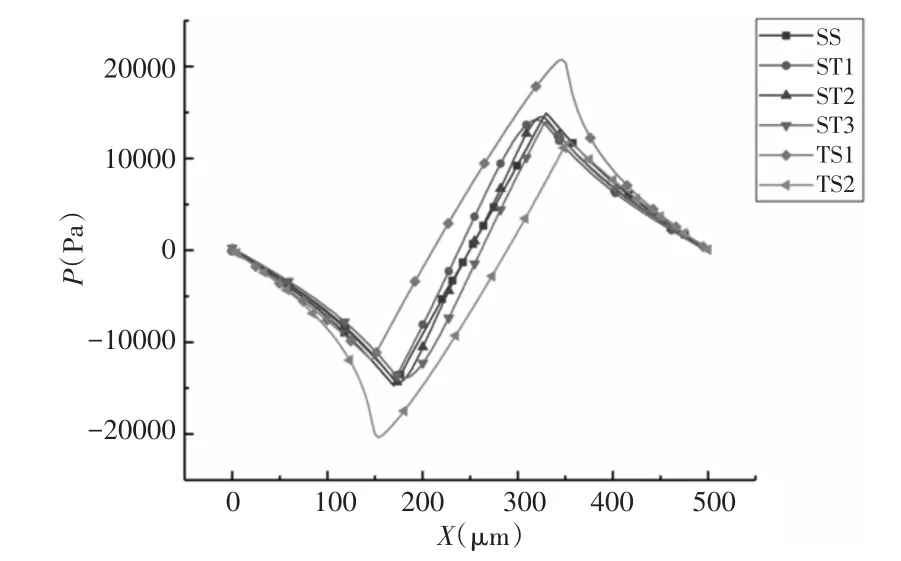
图4 织构上壁面对称轴线处压力分布Fig.4 Pressure Distribution at the Symmetry Axis of the Upper Wall of Texture

不同类型织构压力均沿x方向先降低，在织构入口边缘降至最低，随后压力增大，在织构出口边缘处达到最大值，最后压力降至与前一周期边界压力相同。分别对比ST1、ST3及TS1、TS2两种非对称织构，由于相反的楔形结构，其压力分布关于x轴对称，故表现出相反的动压性能。

3.2 深度比对动压性能的影响

在保持织构其他参数不变的情况下（H0=5μm，U=0.1m/s，L=500μm，Sp=10%），分析深度比对不同楔形织构动压性能的影响。SS上壁面对称轴线处的压力分布曲线，如图5所示。不同类型织构压力幅值随深度比的变化规律，如图6 所示。可以看出，不同类型织构压力分布随深度比的变化规律相近。织构动压性能随深度比的变化规律，如图7所示。对称织构（SS和ST2）的动压性能始终为正，随着深度比的增大，其动压性能先增大后减小，而非对称织构的动压性能表现出明显的差异，楔形收敛织构（ST1、TS1）的动压性能先增大后减小，由于相反的楔形结构，ST3和TS2表现出相反的动压性能变化趋势。其中部分织构的动压性能参数为负，这意味着该类型织构的动压性能不利于提高织构的减磨性能。此外，随着深度比的增大，ST3的动压性能逐渐优于ST1，可以预见的是，当深度比的增大到一定程度时，TS2的动压性能也将优于TS1。这也解释了文献［4］（λ=8）和文献［7］（λ=1.05～1.45）对相同形状织构的模拟结果为何会出现相反的结论。因此，对于单向运动的织构化表面，深度比的选择对楔形织构的动压性能至关重要。

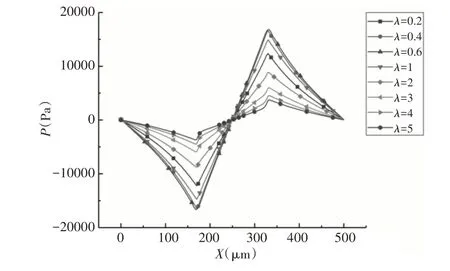
图5 SS上壁面对称轴线处压力分布曲线Fig.5 Pressure Distribution Curve at the Symmetry Axis on the Upper Wall of SS

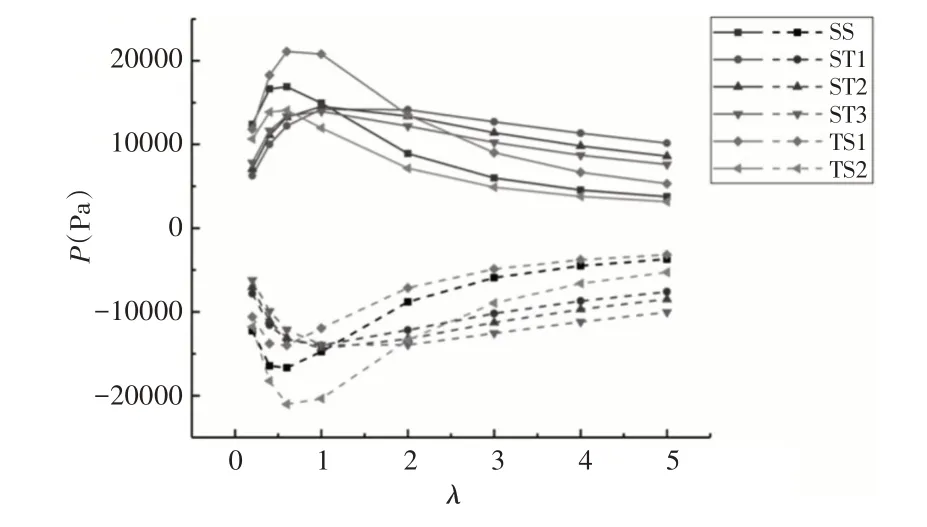
图6 深度比对压力幅值的影响Fig.6 Influence of Depth Ratio on Pressure Amplitude

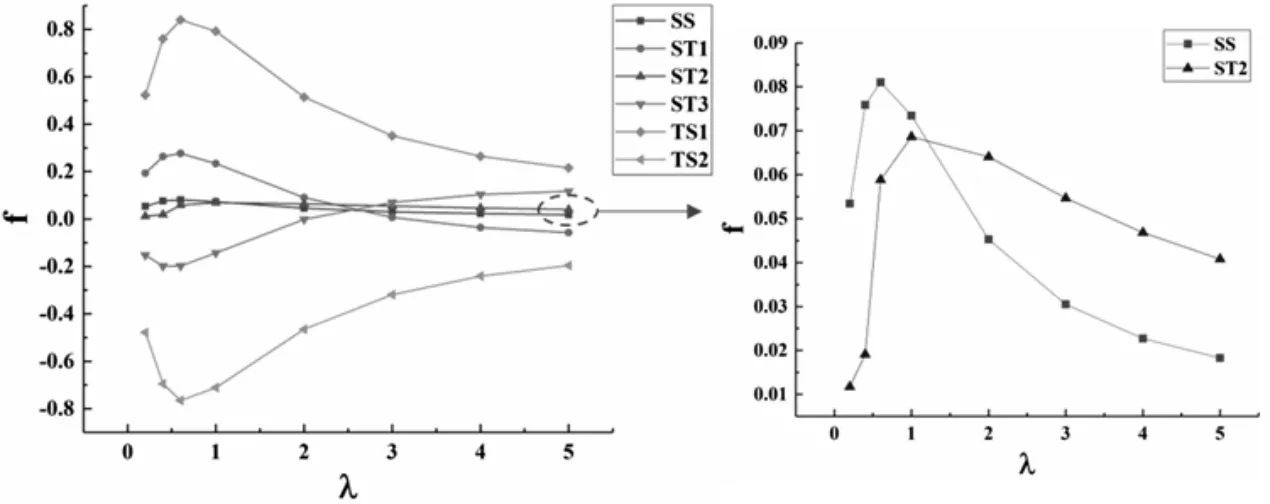
图7 织构动压性能与深度比的变化规律Fig.7 Variation of Dynamic Pressure Properties and Depth Ratio of Texture

SS截面轴线处速度分布曲线及其流线矢量图，如图8、图9所示。随着深度比的增大，织构内部的涡流现象逐渐增强，这是导致织构压力幅值随深度比增大而降低的主要原因。当织构深度比较大时，织构上壁面运动产生的动能一部分将转化为织构内部促进涡流产生的能量，使得润滑液产生附加动压力的能量发生损耗，故压力幅值随织构深度比的增大而减小，织构动压性能也随之降低。此外，在实际工程中，尽管深度比更大的织构意味着储存了更多的润滑液，但织构内部产生的涡流减少了流入摩擦副间隙的润滑液流量，当摩擦副间润滑液不足时润滑状态将发生改变，此时织构很难提供充足的润滑液以改善润滑状态，进而对摩擦性能造成不利影响［9］，因此织构深度比不宜过大。但过小的织构深度比意味着织构不会形成有效的楔形效应以产生足够的附加动压力，当织构深度接近摩擦副油膜间隙时，织构表现出最优的动压性能。

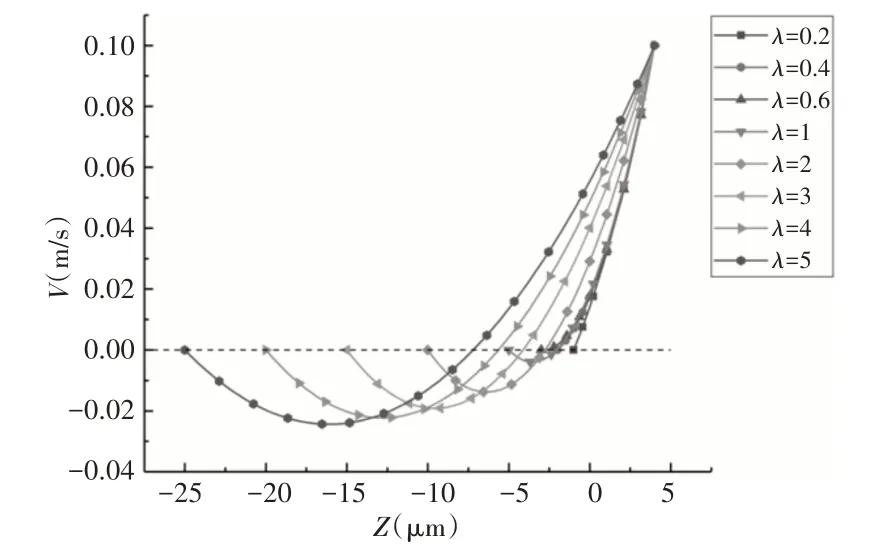
图8 织构截面对称轴线处速度分布Fig.8 Velocity Distribution at the Symmetry Axis of the Textured Section

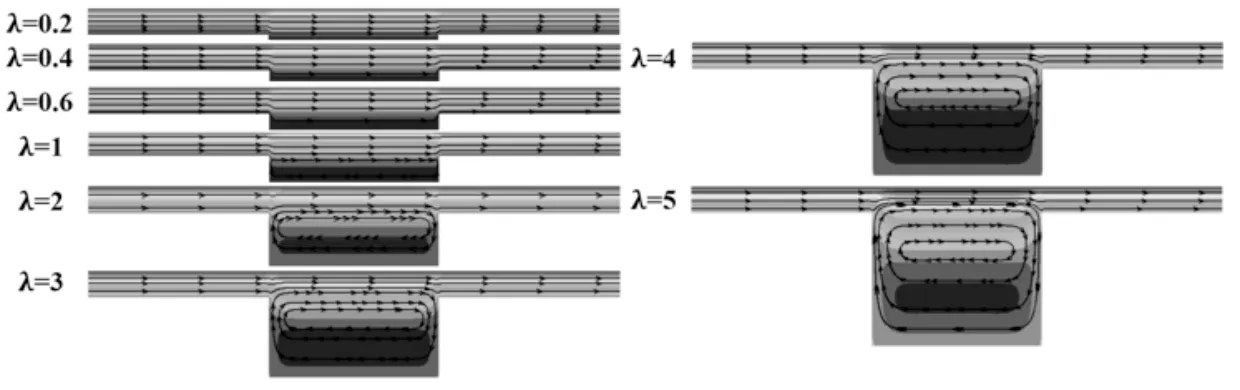
图9 流线矢量图Fig.9 Streamline Vector Diagram

3.3 面积率的影响

在保持织构其他参数不变的情况下（H0=5μm，U=0.1m/s，L=500μm，λ=1），分析面积率对织构动压性能的影响。不同类型织构动压性能随面积率的变化规律，如图10所示。对称织构SS、ST2和楔形收敛织构ST1、TS1的动压性能随面积率的增大而增大，与深度比的影响相类似，楔形结构相反的ST3和TS2的动压性能表现出相反的趋势。由于表面形状的收敛结构，TS1表现出最优的动压性能，在较高的织构面积率时差异更明显，当面积率从10%提高到30%时，其动压性能提高了8.04倍，而截面形状收敛的ST1为6.05倍，对称织构SS仅为3.95倍。TS1上壁面轴线处压力分布曲线图，如图11所示。可以看出随着织构面积率的增大，负压幅值变化幅度较小，而正压幅值明显增大。这是因为当面积率增大时，更多的润滑液流向织构收敛端，而收敛的表面形状对润滑液流量的影响远大于截面形状，因此表面形状收敛的织构在收敛端产生了更高的正压力，进而表现出更强的动压性能。另一方面，当织构面积率较小时，进出口周期边界处的压力为零，这意味着该织构并未受到前后相邻织构的影响。当面积率增大到一定程度后，该织构单元将会受到相邻织构的影响，由于后一织构负压区的泵吸作用［10］，使得前一织构的润滑油产生额外的流量进入后一织构，从而进一步提高了附加动压力，因此织构出入口边界处的压力明显提高。相较于正方形，表面形状为正三角形的织构最大特征长度及宽度更大，这意味着当面积率相同时正三角形织构更易受到相邻织构的影响。

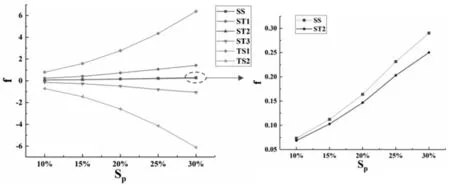
图10 织构动压性能与面积率的变化规律Fig.10 Variation of Dynamic Pressure Properties and Area Ratio of Texture

图11 TS1上壁面对称轴线处压力分布曲线Fig.11 Pressure Distribution Curve at the Symmetry Axis of TS1 Upper Wall

由于不同类型织构内部流体速度分布随面积率的变化规律相同，故仅展示SS截面对称轴线处的流体速度分布，如图12所示。可以看出织构内部涡流随着面积率的增大而逐渐减弱，这是由于织构相对于运动方向的特征长度变大，上壁面运动时产生的动能更易传递到织构底部以带动润滑液流动，从而削弱了涡流现象。不同类型织构在相同条件下截面的流线矢量图及其涡流中心所在竖直方向上的速度分布，如图13所示。可以看出，相同面积率时TS1和TS2具有相较于其他类型织构更大的特征长度，其织构内部涡流程度更低，这与之前的结论相符合。此外，分别对比ST1、ST3和TS1、TS2两类楔形相反的织构，可以看出，不同的楔形织构内部涡流分布各不相同，但其涡流大小并未因此而存在明显差异。

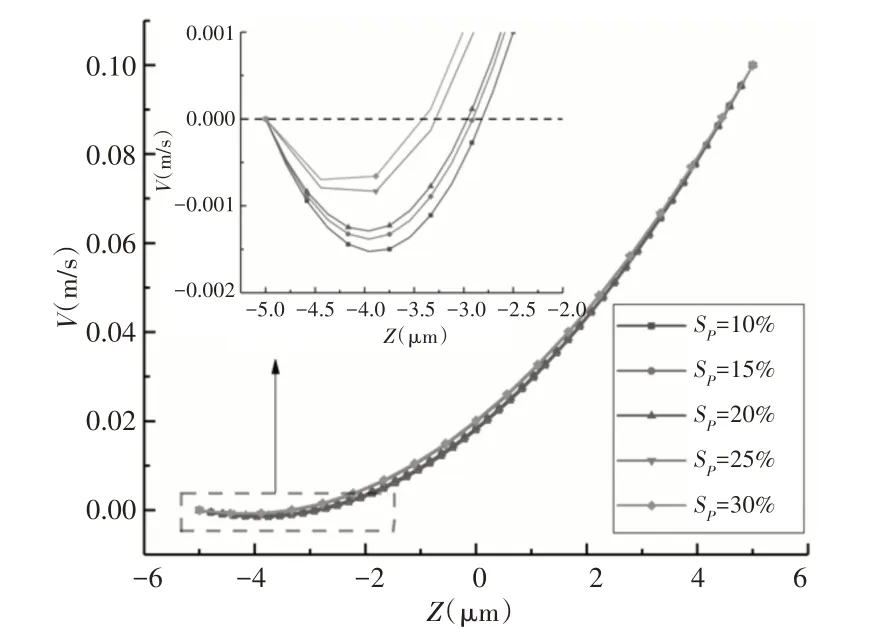
图12 SS织构截面轴线处速度分布Fig.12 Velocity Distribution at the Axis of SS Texture Section

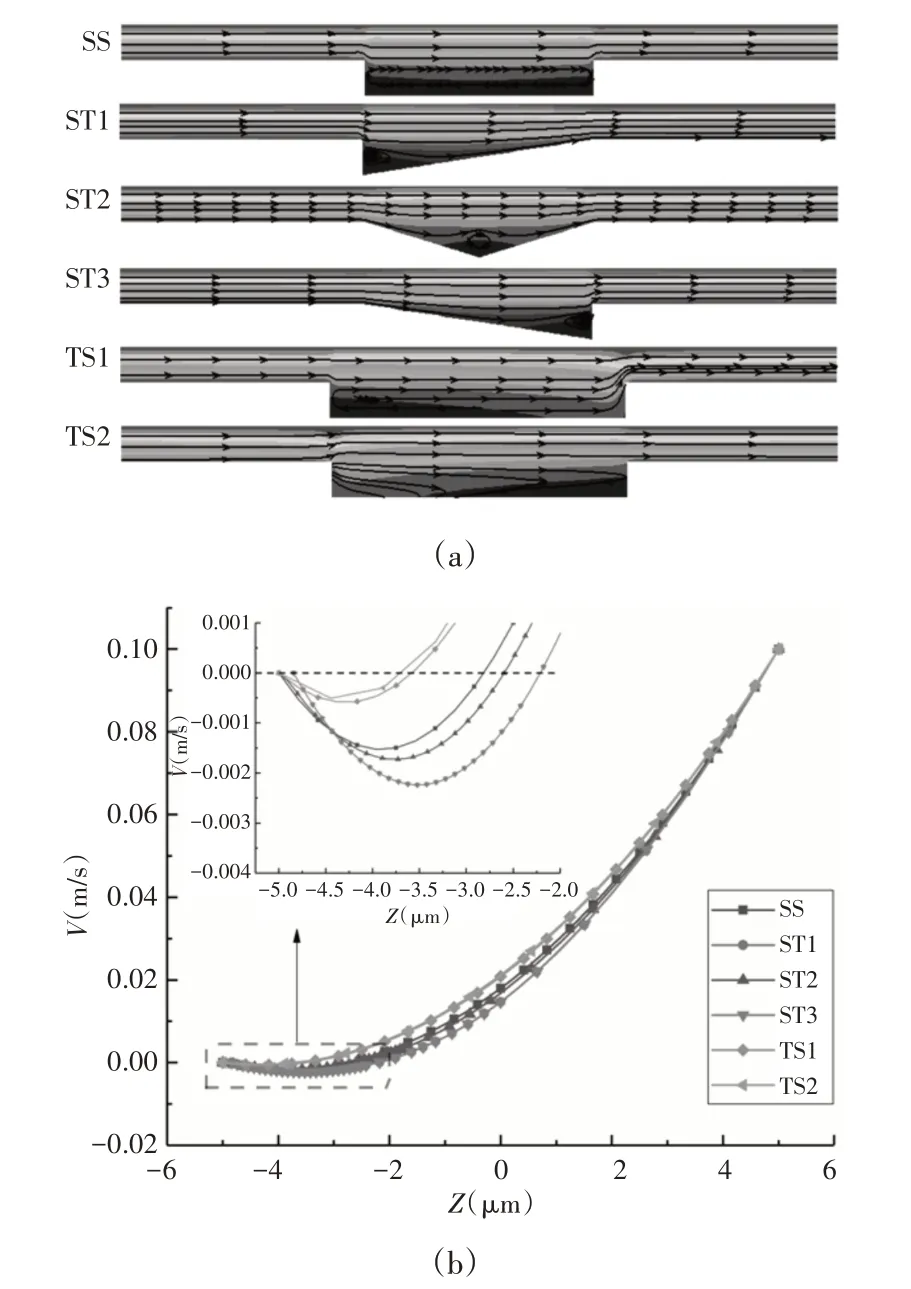
图13 不同类型织构流线矢量图和速度分布图Fig.13 Streamline Vectors of Different Types of Texture and Velocity Distribution Diagram

尽管从数值模拟的结果可以看出面积率越大，织构动压性能越强，但并不意味着面积率可以一味的增大。这是因为织构负压幅值一般随面积率的增大而增大，当负压降至润滑液空化压力时，将会发生空化现象，此时流体压力分布的不对称会产生额外的承载能力，进一步提高织构的动压性能。然而，空化现象发生时润滑液中析出的气泡会导致织构内壁出现气蚀等现象，从而影响织构自身寿命［11］。另外从其他试验研究来看，织构面积率的增大也会导致表面间接触应力的增大，进而加剧织构退化和磨损，当织构受到破坏时，其减磨性能将会大大降低［12-13］，因此织构面积率存在一个最优值且该最优值与摩擦副材料自身性质有密切关系。

4 正交模拟计算

由上述可知，织构化摩擦副的摩擦性能与织构的几何参数及楔形结构密切相关，因此有必要研究表面形状、截面形状、深度和面积率对动压性能的影响程度，为织构设计优化提供参考，因此，采用L9（34）正交表进行数值模拟参数设计。分析结果，如表1、表2所示。在相同工况条件下，各因素对动压性能影响的主次顺序依次为：表面形状＞面积率＞截面形状＞深度比，对负压幅值影响的主次顺序依次为：深度比＞截面形状＞表面形状＞面积率。

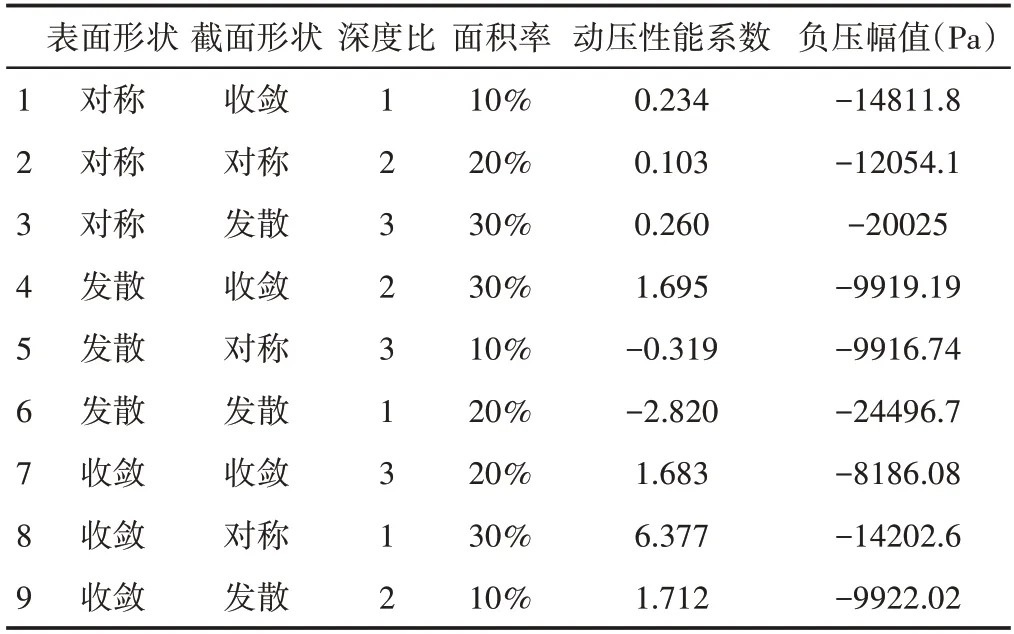
表1 正交分析表Tab.1 Orthogonal Analysis Table

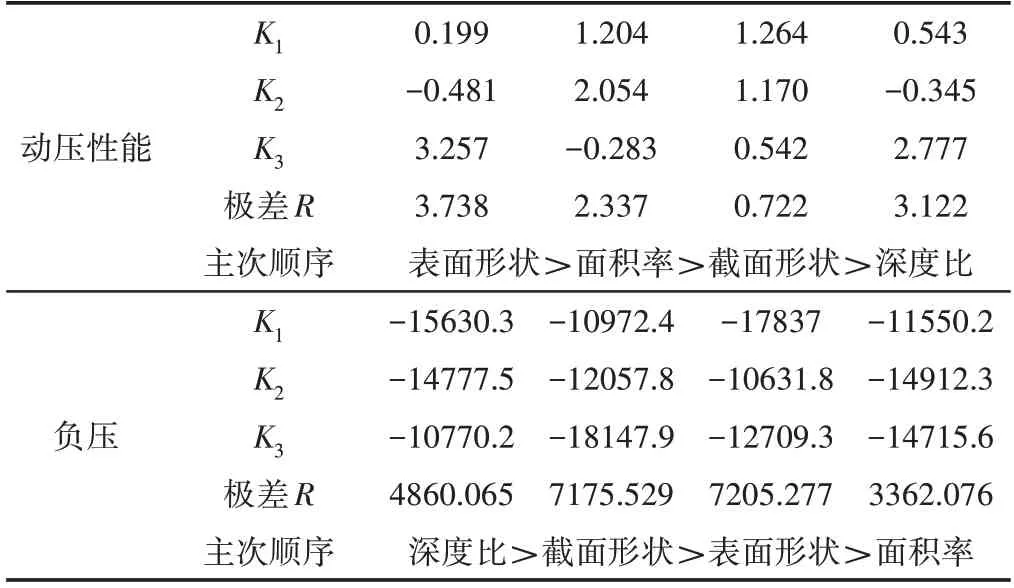
表2 极差分析表Tab.2 Range Analysis Table

另外从正交分析表可以看出，当表面形状和截面形状均为楔形收敛时，并未表现出最优的动压性能。因此不能一味的考虑楔形收敛结构带来的正压影响，同时也需要考虑几何参数对楔形效应及压力影响区面积等因素的影响。

5 结论

这里采用基于N-S 方程的CFD 方法，通过单因素分析和正交模拟，研究了织构几何参数对不同楔形结构的织构动压性能的影响，结果如下：

（1）表面织构的楔形结构对动压性能有显著影响，对称织构始终表现出利于减磨的动压性能，而楔形织构的动压性能与几何参数密切相关。（2）随着织构深度比的增大，对称及楔形收敛织构的动压性能先增大后减小，深度比越大，涡流现象越剧烈，对织构动压性能的削减程度越大。而楔形发散织构的动压性能表现出相反的趋势，当深度比增大到一定程度后，其动压性能将优于楔形收敛织构。（3）随着织构面积率的增大，对称及楔形收敛织构的动压性能随之增大，同时，织构内部涡流现象逐渐减弱。但过大的面积率会导致空化现象的发生及较大的接触应力，加速织构的退化及磨损。（4）同一工况下，几何参数和楔形结构对织构动压性能影响的主次顺序依次为：表面形状＞面积率＞截面形状＞深度比，对织构负压幅值影响的主次顺序依次为深度比＞截面形状＞表面形状＞面积率。