新型无井道双立柱电梯纵向振动特性分析
2024-02-29李彦彦郭志强张志刚
李彦彦,张 柳,郭志强,张志刚
(郑州轻工业大学机电工程学院,河南 郑州 450002)
1 引言
老旧小区改造,加装电梯是刚需,能够有效解决居民上楼难、特别是老年人上下楼困难等问题。新型无井道双立柱电梯结构简单,无需建设现有电梯所需的井道和固定廊道,对一楼用户遮挡光线少,费用低,比较适合目前正在改造的老旧小区。
提高电梯运行的平稳性和乘坐的舒适感,减少电梯运行过程中产生的振动和噪声,是目前电梯发展急需解决的问题。对于传统曳引式电梯,其纵向振动特性研究较多。文献[1]对曳引比为2:1的电梯建立了9自由度的动力学模型,采用定步长龙格—库塔法求解出轿厢振动响应,结果表明电梯在起、制动阶段加速度变化较大。文献[2]考虑了电梯曳引绳刚度具有时变特性,运用频率可靠性灵敏度相关理论,结合人工神经网络技术和模态分析方法,给出改变绳头弹簧刚度和曳引机的隔振垫的刚度,可有效降低共振。文献[3-4]给出系统各参数对固有频率的影响规律,得到了各种工况下的振动曲线与系统各参数对轿厢响应的影响规律。
新型无井道双立柱电梯作为一种新型电梯,目前该电梯纵向振动方面的研究较少。以该新型电梯为研究对象,考虑双立柱的刚度及曳引绳刚度具有时变特性,建立其纵向振动动力学模型,根据动力学微分方程,计算得到该电梯的固有频率和谐波激励下的响应幅值,给出系统的固有频率和谐波响应幅值随承载质量、轿厢位置变化的规律,有助于对电梯系统进行动态特性优化、减振降噪等分析,提高该电梯系统的运行性能。
2 新型无井道双立柱电梯结构设计
新型无井道双立柱电梯在结构设计上,与传统电梯有较大区别。传统曳引式电梯主要由曳引系统、导向系统、轿厢系统、门系统、重量平衡系统、电力拖动系统、电气控制系统等组成[5-6],如图1所示。新型无井道双立柱电梯主要由双立柱轨道、轿厢、对重、机房和控制系统五个部分组成,如图2所示。其中,双立柱为电梯支撑部分,同时保证轿厢在其上面滑动。双立柱上附着有对重块,可平衡轿厢的重量。轿厢部分装有一块踏板,当轿厢停到指定楼层时能展开与入户通道相连接,省去了每户的廊道。机房部分为电梯的动力部分,为轿厢的提升与下放提供动力。

图1 传统电梯结构图Fig.1 The Structure Diagram of Traditional Elevator

图2 新型无井道双立柱电梯结构图Fig.2 The Structure Diagram of the New Double Column Elevator Without Shaft
新型无井道双立柱电梯的优点主要有以下几个方面:
(1)轿厢不用附着墙壁运行,无需建设电梯井道;
(2)跟随轿厢一起运动的收纳式空中廊道设计,入户门与轿厢空中廊道对接,实现平层入户,突破了需建设固定连接走廊、只能半层入户的局限,能最大限度地减小对原有建筑的破坏,对一楼用户采光影响小;
(3)新型无井道双立柱电梯采用了巧妙的机构及传动方式:电梯轿厢开门机构采用锥齿轮传动,实现对开;电梯踏板采用减速电机转轴带动踏板,可以精确转到指定位置。
3 建立新型无井道双立柱电梯纵向振动模型及动力学方程
3.1 新型无井道双立柱电梯系统纵向振动模型
曳引式电梯根据传动方式的不同,可分为曳引比为1:1和2:1 两种[6-9],新型无井道双立柱电梯属于曳引比为2:1 的电梯系统。该电梯是一个复杂的无限自由度的连续性系统,与传统的曳引式电梯相比,由于没有井道,双立柱是主要支撑承重梁的部件,需要考虑双立柱的刚度,这里立柱选用型号为28c的槽钢。在电梯运行过程中,曳引钢丝绳的长度、轿厢承载质量都会发生变化,因此电梯系统是一个时变系统。若忽略曳引钢丝绳长度及轿厢承载质量的变化,分析得到的结果就会与实际情况有偏差。将电梯系统进行时域离散化处理,假设在每个时间段内电梯系统的参数不变。电梯系统从曳引机到轿厢由多个隔振环节组成,忽略钢丝绳的质量,对曳引机底橡胶垫、轿底橡胶垫等进行等效简化[7],建立电梯系统纵向方向8自由度动力学模型,如图3所示。
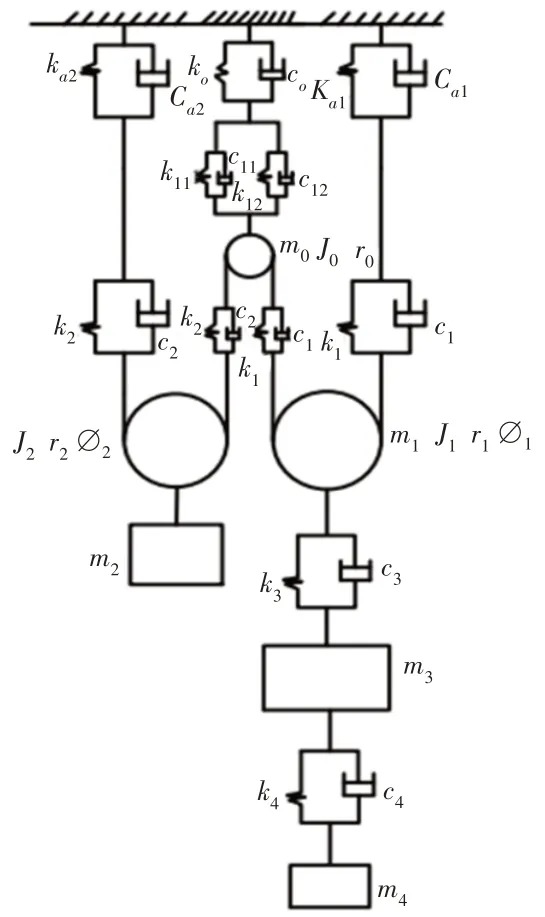
图3 纵向振动模型Fig.3 The Longitudinal Vibration Model
对该模型的参数符号说明如下:
m0、J0、r0—曳引装置与导向轮的质量、转动惯量和曳引轮绳槽半径;m1、J1、r1—轿顶轮的质量、转动惯量和轿顶轮绳槽半径;m2、J2、r2—对重与对重轮的质量、转动惯量和对重轮绳槽半径;m3、m4—轿厢架与附件质量、轿厢体与承载质量;k0、c0—承重梁及减振垫折合后的刚度与阻尼;kl1、cl1—左侧立柱折合后的刚度与阻尼;kl2、cl2—右侧立柱折合后的刚度与阻尼;kz、cz—承重梁及减振垫与双立柱折合后的刚度与阻尼;k1、c1—轿厢架与曳引轮之间曳引钢丝绳的等效刚度与阻尼;k2、c2—对重与曳引轮之间曳引钢丝绳的等效刚度与阻尼;ka1、ca1—轿厢架端曳引钢丝绳的绳头刚度与阻尼;ka2、ca2—对重端曳引钢丝绳的绳头刚度与阻尼;k3、c3—轿顶轮与轿厢架之间橡胶的刚度与阻尼;k4、c4—轿厢与轿厢架之间橡胶的刚度与阻尼。
3.2 新型无井道双立柱电梯系统运动微分方程
根据机械振动理论[10],建立该电梯系统纵向振动的运动微分方程,即:
写成矩阵的形式,即:
其中:
3.3 新型无井道双立柱电梯系统主要参数
3.3.1 曳引钢丝绳的等效刚度系数
新型无井道双立柱电梯在纵向运动过程中需要使用曳引钢丝绳,由于曳引钢丝绳具有弹性,为求解方便,将其简化为弹簧-阻尼系统。将钢丝绳按长度进行等分,离散为若干弹簧的串联。设该曳引钢丝绳的等效刚度为k(t),可看成n根钢丝绳并联[3],(lt)为曳引轮和轿架之间钢丝绳的长度,则:
式中:n—钢丝绳根数;E—钢丝绳的弹性模量(N/m2);A—横截面面积(m2)。
各段钢丝绳的等效刚度为:
钢丝绳与绳头弹簧串联后等效刚度为:
式中:h—最大提升高度;ka11—对重端曳引钢丝绳与绳头弹簧串联后的等效刚度;ka22—轿厢端曳引钢丝绳与绳头弹簧串联后等效刚度。
3.3.2 双立柱的等效刚度系数
从力学角度分析立柱属于压杆,每根立柱的刚度系数就是使该杆端产生单位位移时所需施加的杆端力,两根立柱可看成并联,其刚度系数分别为:
双立柱与上面的承重梁部分进行串联,串联后刚度系数kz为:
3.3.3 新型无井道双立柱电梯系统主要参数
该电梯系统的主要参数,如表1所示。

表1 新型无井道双立柱电梯系统主要参数Tab.1 The Major Parameter of the New Double Column Elevator without Shaft
3.3.4 其他参数说明
该电梯系统多用于多层建筑,提升距离短,属低速电梯,选择电梯运行速度为1m/s。根据电梯系统的载重及速度,选取曳引机的转动频率为20Hz。
4 新型无井道双立柱电梯系统纵向固有频率分析
研究多自由度振动系统的固有频率时,一般忽略系统的阻尼和外界激励,动力学微分方程(2)则变为:
式(8)对应的特征矩阵方程有非零解的充要条件是其系数行列式为0,即:
式(9)有n个正实根,对应于系统的n个固有频率[10]。
利用Matlab软件编程计算得到该系统的各阶固有频率,第一阶固有频率很小,第八阶固有频率大于60Hz,该振动对人体影响较小,因此主要分析第二阶到第七阶的固有频率。电梯系统随轿厢位置、承载质量变化时各阶固有频率的变化曲线,如图4所示。
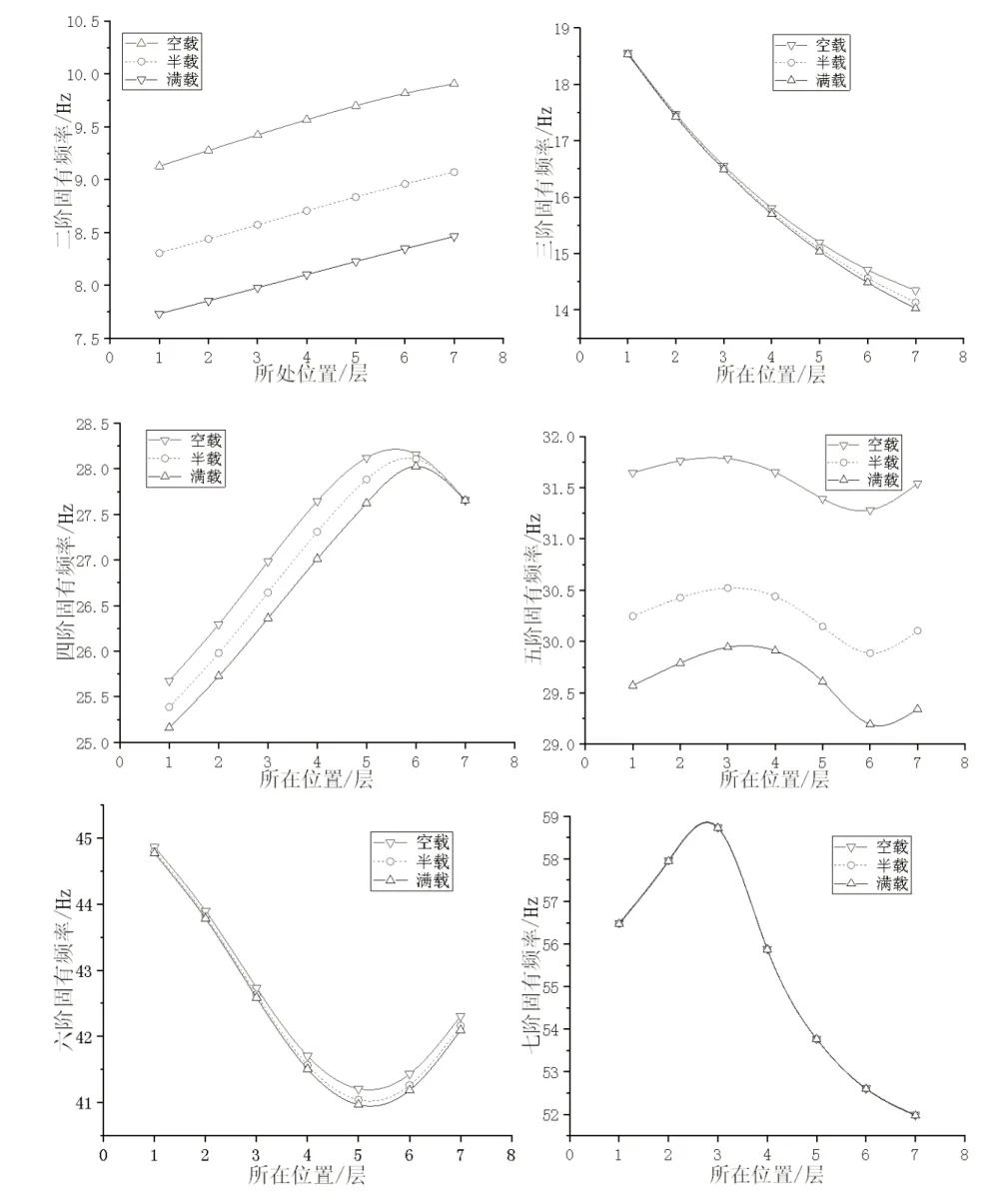
图4 各阶固有频率随承载质量与高度的变化曲线Fig.4 The Natural Frequencies of Each Order Varying with Bearing Mass and Height
由4图可得出以下结论:
(1)曳引钢丝绳长度的变化(即提升高度)对固有频率影响较大。第三阶、六阶、七阶固有频率随曳引绳长度增加变化较大,且基本上随曳引绳长度增加而减小,第二阶、四阶固有频率随曳引绳长度增加而增大。以空载工况为例,在轿厢提升过程中,第三阶、六阶、七阶的固有频率分别从18.559Hz 减小到14.343Hz、44.863Hz 减小到41.210Hz、58.741Hz减小到51.989Hz。第二阶、四阶固有频率分别从9.127Hz增至9.907Hz、25.676Hz增至28.161Hz。
(2)各阶固有频率随承载质量变化较小,但第二阶、五阶固有频率随承载质量变化稍大,各阶固有频率基本上随承载质量的增加呈减小趋势。以中间层为例,随承载质量增加,第二阶、五阶固有频率分别从9.566Hz减小到8.101Hz、31.649Hz减小到29.910Hz,乘客的上下对固有频率影响较小。
(3)各阶固有频率与曳引机的转动频率20Hz相差较多,不会出现共振现象,电梯系统的振动较小,舒适性比较好。若系统的某阶固有频率与曳引机的转动频率接近,可通过改变系统的一些参数来调整固有频率,避免共振出现。
5 新型无井道双立柱电梯系统纵向谐波响应分析
电梯系统的谐响应主要分析电梯系统在承受谐波激振力时的稳态响应,避免电梯系统出现共振现象,确保电梯系统运行的安全性与舒适性[7]。
5.1 谐波激励下的响应求解方法
该电梯系统在谐波激励下的运动微分方程为式(2),该式也可表示成如下形式:
式中:F—谐波激励力的振幅向量;
ω—激振频率。
电梯系统的谐响应主要是研究电梯轿厢对于系统各参数变化时的稳态响应规律,因此主要研究上述微分方程的特解。
5.2 电梯系统的谐波响应分析
谐波响应分析是分析系统受到随时间变化的谐波激励时的响应。轿厢的振动是影响电梯系统安全可靠性的重要因素,因此电梯系统的谐波响应分析主要是针对轿厢,而轿厢振动的幅值是分析的主要内容。
曳引系统为电梯系统运行提供动力,但也会引入复杂的激励,导致电梯系统产生受迫振动。曳引系统引入的激励形式较复杂,激励产生的原因包括曳引机电机转子的不平衡、曳引轮及制动轮的偏心和机座的微小变形等,这些因素会引入受迫激振力。由于曳引机是主要的激振源,对曳引机施加幅值为1000N、频率为(2~20)Hz 的正弦激励,通过计算可得到电梯轿厢在不同承载质量、轿厢处于不同位置的振动响应幅值随激振频率变化的规律。根据5.1 的方法,利用MATLAB 软件进行编程,计算得到轿厢在不同工况下的振动幅值,如图5~图7 所示。
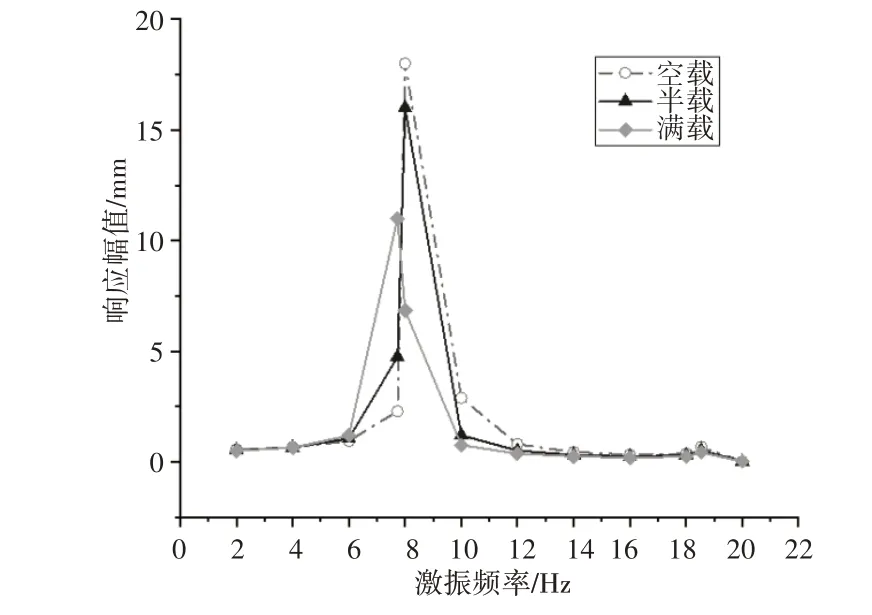
图5 轿厢位于底层Fig.5 The Car Located on the Ground Floor

图6 轿厢位于中间层Fig.6 The Car Located on the Middle Floor
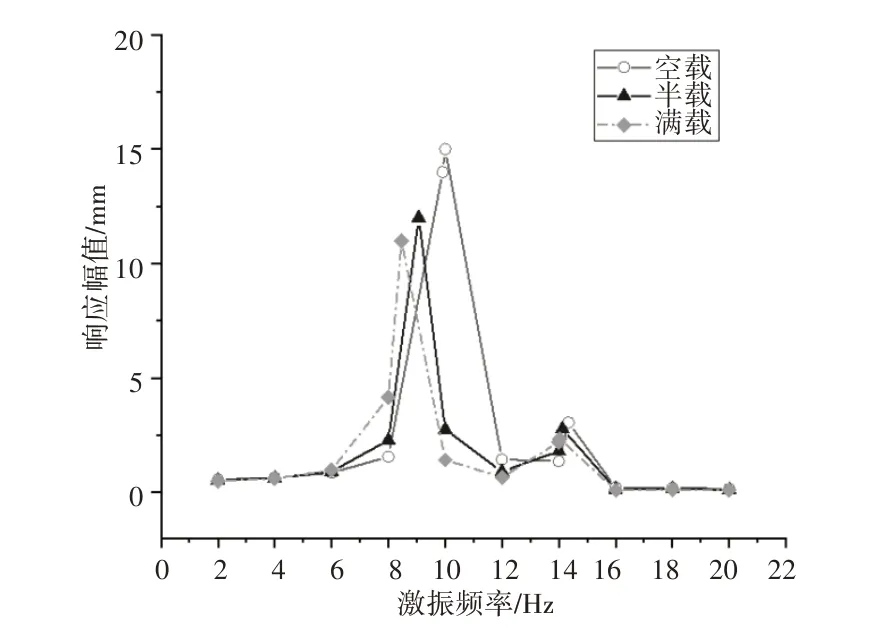
图7 轿厢位于顶层Fig.7 The Car Located on the Top Floor
由图5~图7可得到以下结论:
(1)当激振频率与电梯系统的固有频率接近时,轿厢的振动幅值很大,最大可达18mm,会出现瞬态共振现象。空载时振动幅值最大,满载时振动幅值最小。
(2)轿厢位于中间层时,当激振频率接近系统二阶固有频率(9Hz左右),轿厢的振动幅值最大为16mm。当激振频率接近系统三阶固有频率(16Hz左右)时,轿厢的振动幅值最大为3.066mm,远小于激振频率接近系统二阶固有频率的振动幅值。在电梯系统运行的过程中,二阶固有频率附近的振动幅值一直都很大,是影响该电梯系统性能的最重要的频率,因此二阶固有频率将是该电梯系统主要减振的频率成分。
(3)当激励频率远离电梯系统的固有频率时,如图5~7所示,轿厢的振动幅值较小。
6 结论
以新型无井道双立柱电梯为研究对象,将系统简化为8 自由度动力学模型。利用机械振动理论,建立电梯系统动力学方程,得到该电梯系统在不同承载质量、轿厢处于不同位置的各阶固有频率的变化规律,该电梯系统的二、三阶固有频率在(7.731~9.907)Hz、(14.023~18.559)Hz,曳引机的转动频率远离该电梯系统的固有频率,共振现象可避免。当电梯系统受到谐波激励时,得到电梯系统在不同承载质量、轿厢处于不同位置时轿厢振动幅值的变化规律,当激振频率与电梯系统的二阶固有频率接近时,会出现瞬态共振,且轿厢最大振动幅值为18mm,因此二阶固有频率是该电梯系统减振分析的主要频率成分。根据电梯系统的固有频率计算与谐波响应分析,可通过改变电梯系统的参数进行优化设计,降低电梯系统振动的幅值,为改善新型无井道双立柱电梯系统的安全可靠运行及乘坐舒适性提供合理有效的建议。
