几何变换在圆柱度评定优化算法中的研究
2024-02-29尹浩田曹满义吴江昊
尹浩田,郑 鹏,曹满义,吴江昊
(郑州大学机械与动力工程学院,河南 郑州 450001)
1 引言
零件的形位误差对产品精度有至关重要的影响。对于仪表等精密器械,其组成部件应严格满足形位误差的设计要求。轴类零件在机械产品中应用广泛,圆柱度作为衡量回转体零件形位误差的重要指标,将对产品的旋转精度和寿命产生重要影响。因此,实现圆柱度误差迅速、准确地评定对提高生产效率至关重要[1]。圆柱度误差的评定方法主要有:最小包容区域法(MZC)、最小外接圆柱法(MCC)、最大内切圆柱法(MIC)、最小二乘法(LSC)四种[2]。其中,最小二乘法在计算速度上相较于其他方法有明显的优势,但往往其误差评定结果不能满足精度要求。最小包容区域法满足圆度评定的包容要求,得到的误差精度高,但其运算较为繁琐,评定效率低,常作为误差评定标准。近些年来随着深度学习和人工智能的不断发展,有不少研究学者对于圆柱度误差评定提出了新方法。文献[3]实现了利用DNA方法计算圆柱度误差,并通过实验进行验证。文献[4]利用鞍点规划和遗传算法,构建了直接求解形位误差的线性规划模型。文献[5]研究了粒子群优化算法在圆柱度误差中的应用,通过求解模型实现圆柱度误差评估。文献[6]通过误差分离技术(EST)设计了圆柱度误差在线检测装置并进行实验验证;文献[7]提出了一种基于收缩因子的粒子群优化算法来评价最小区域形状误差。文献[8]提出了一种改进的协调搜索(IHS)算法来提高圆柱度的测量精度。文献[9]提出了一种基于运动几何优化算法(KGOA)的圆柱度最小区域误差评估方法。利用上述算法,在测量数据充足的情况下可以很容易地进行圆柱度误差评定。
最小包容区域圆柱度误差求解可通过构建优化函数实现。但在实际评定中,由于圆柱度的精确原位测量比较复杂,需要对圆柱度进行测量和重构,并对圆柱度进行评定[10]。这里针对最小包容区域法运算速度慢和最小二乘法精度低的问题,将求解最小包容区域法圆柱度误差的三维方法转化为求解平面度的二维方法,在保证精度的前提下提高了计算速度。
2 圆柱度误差几何模型
由圆柱度误差的定义所知,在圆柱度误差评定过程中既要满足最小条件原则,又要在基准圆柱面的基础上得到被测要素的变化量。被测要素Pi始终位于同轴的两理想圆柱面C1和C2之间,如图1所示。当C1和C2的差值最小时,其差值t即为最小区域法所求得的圆柱度误差。
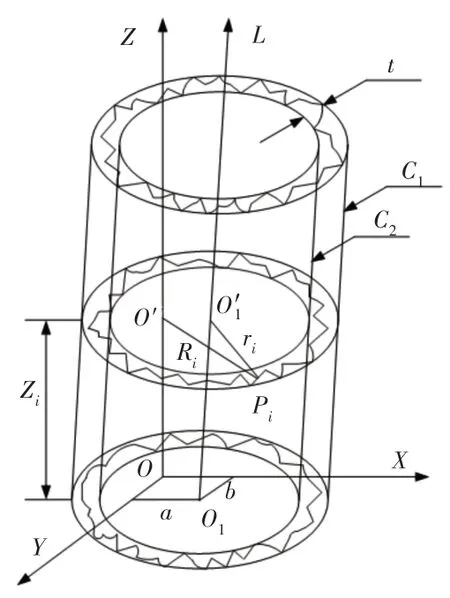
图1 圆柱度误差几何模型Fig.1 Geometric Model of Cylindricity Error
柱面坐标系中工件的三维表面数据的采集方式多采用截面法,即沿轴向进行等间距采样,测量多个截面后,对整体数据进行拟合。设实际被测圆柱面各点的坐标为P(iRi,θi,Z)i,仪器的测量回转轴线OO'沿Z轴方向,如图1 所示。评定基准圆柱轴线O1O'1沿L轴方向,其在XOY平面上的偏心坐标为(a,b)。设L轴与Z轴的夹角为γ,其在XOZ、YOZ平面上的投影分量分别记为γx、γy,则理想圆柱面的参数方程可以表示为:
以L为基准,保证实际被测点处于圆柱面C1和C2之间,通过不断调整轴线L的偏心坐标和夹角,求得具有最优位置和方向的轴线L’,并以此为基准轴线做最大最小包容圆柱面,即可求得圆柱度误差值。此过程可转化为线性规划求极值问题,通过被测点的点集{P}i得到(a,b,p,q)使其满足于式(2),即可通过求解模型获得圆柱度误差值。
最小包容区域法评定模型为:
3 基于几何变换的圆柱度评定新算法
通过对测量数据进行最小二乘拟合,可以得到被测零件的最小二乘轴LLS。将最小二乘轴线与参考轴线进行坐标变换,可以得到实际被测点经几何变换后的坐标,如图2所示。最小二乘拟合方法是通过最小化所测数据与理想圆柱面的残差平方和来确定参考轴线的最佳匹配函数。拟合过程可理解为通过调整理想圆柱面不断逼近采样数据,使映射点之间的距离不断减小,最终得到的理想轴为最小二乘轴线。
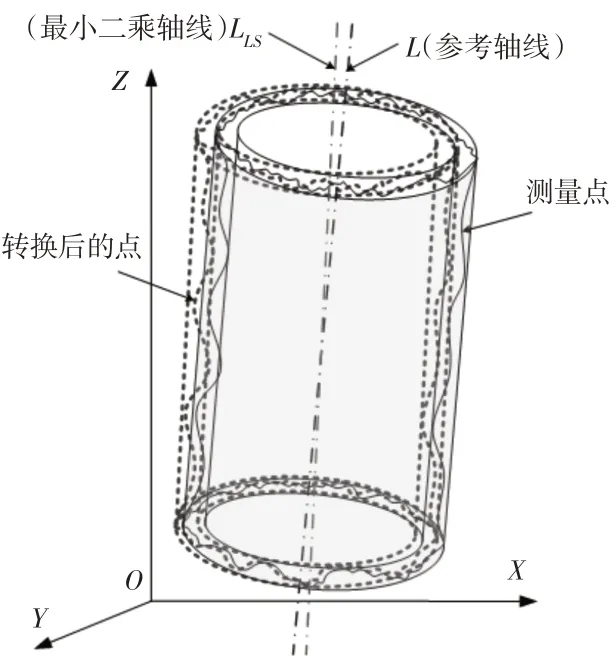
图2 基于最小二乘轴线的坐标变换Fig.2 Coordinate Transformation Based on Least Squares Axis
这里提出的基于几何变换的圆柱度评定优化算法的步骤是:首先利用最小二乘轴线LLS将测量点集(Ri,θi,Z)i进行几何变换,得到转换后的被测点坐标(Ri',θi',Zi')。将转换后的坐标值基于最小二乘轴线展开成平面集(X',Y',Z'),并按照最小包容区域法的评定模型进行求解,计算所得的平面度误差值即为经几何变换后的圆柱度误差。求解过程,如图3所示。
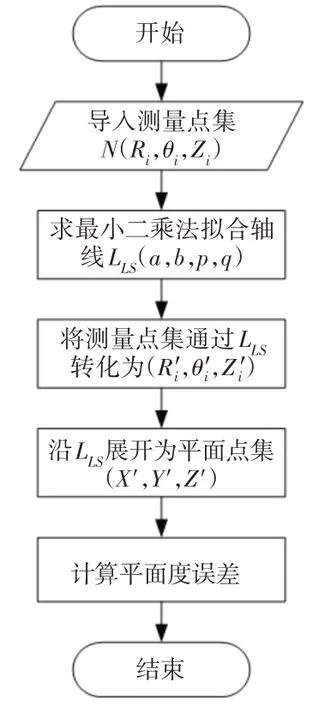
图3 几何变换求圆柱度流程图Fig.3 Flow Chart for Calculating Cylindricity by Geometric Transformation
在实际测量中,由于回转轴线与基准轴线不重合,采集到的圆截面数据会呈规律性变化。图3显示的是实际圆柱的测量过程,其基准轴线与测量回转轴线的夹角为ψ。在此形态下,测头与圆柱面做相对运动,由测头记录测量数据。
由于圆柱面存在倾斜,所测得的轮廓曲线展开后是正弦曲线,如图4所示。
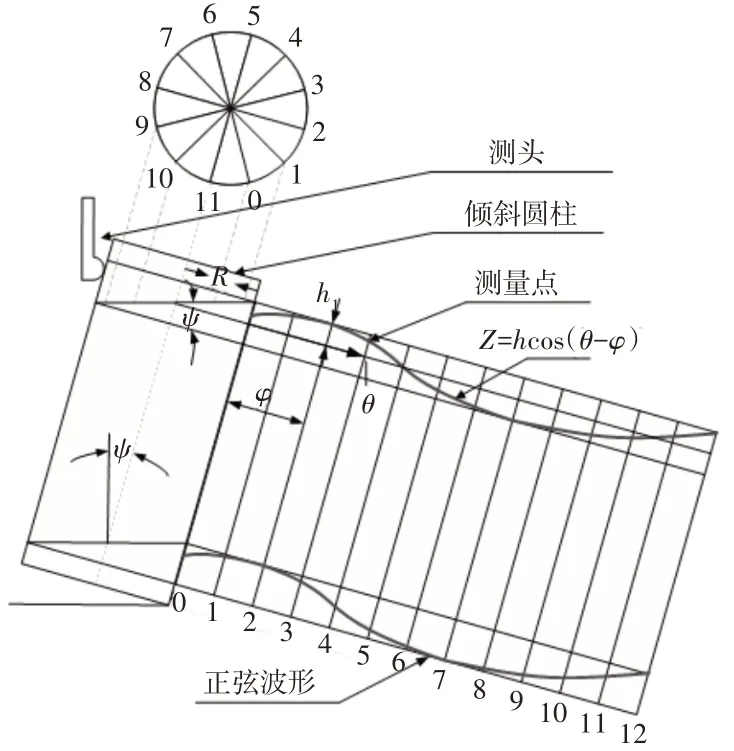
图4 测量点展开图Fig.4 Expanded View of Measuring Points
正弦波的振幅h可表示为:
正弦波Z的方程可以表示为:
式中:θ—展开面上的角坐标;φ—相位。
Z的坐标可表示为:
考虑到圆柱的倾角ψ和正余弦波的振幅呈线性变化,令:
通过数学变换,最终将圆柱度误差转化为求解平面度误差,圆柱度误差值转换为正弦波振幅h,如图5所示。其中,Z1,Z2,…,Zn—n个被测截面数据所展开的正弦曲线,θ—展开面上的角坐标。平面度误差最小包容区域法的数学模型为:
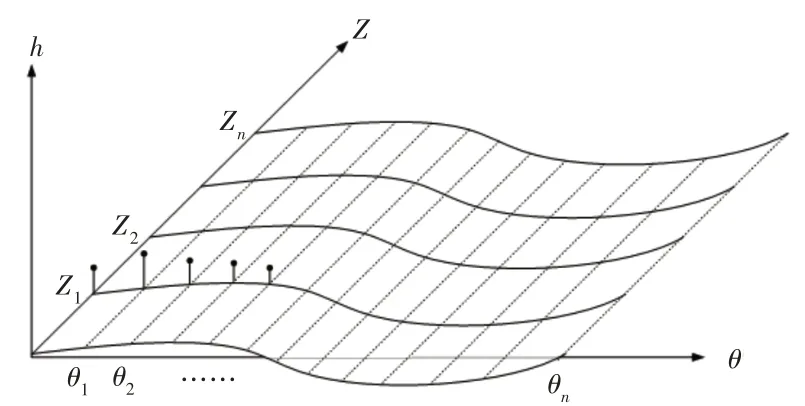
图5 展开表面的网格和数据点Fig.5 Grid and Data Points of the Unfolded Surface
式中:w—实测的原始偏差;x、y—被测点的坐标;u、v—误差的最大和最小值;α、β—绕x、y轴的旋转量;m—测量点个数。
4 实验分析
为验证提出的圆柱度评定方法的准确性,设计并进行相关实验进行圆柱度评定,计算并记录评定效率。测量装置选择DTP-1000AE 型圆度仪,系统精度≤0.06μm。工件选择尺寸为Φ50×42mm,材质为45#并完成精磨加工的轴类零件。实验共测量50个零件,每个零件等间距划分15个截面,获得测量数据。将测量数据分别利用标准评定方法和几何变换法进行评定,实验装置,如图6所示。

图6 实验装置Fig.6 Experimental Setup
将实验数据运用Matlab 仿真分析,分别得到最小包容区域法的三维显示,和展开后的拟合平面,如图7 所示。图中x,y,z是测量点的三维坐标,如图8 所示。为了更直观的观察圆柱度误差评定,图7、图8 中三维坐标系中的测量数据去掉了平均半径。如图7 所示,从中可以看出两同轴圆柱之间包含了所有采样点,它们的半径差即为该工件的圆柱度误差。如图8所示,取圆柱度截面个数为15,采样点数为1000时将测量点展开形成的拟合平面。
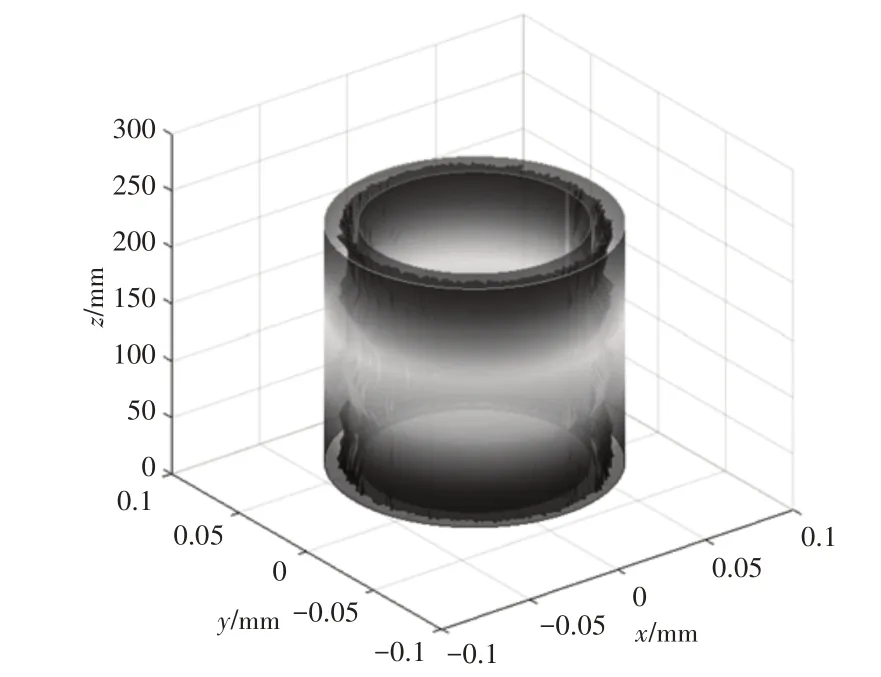
图7 最小区域拟合的圆柱度Fig.7 Cylindricity of the Smallest Area Fit
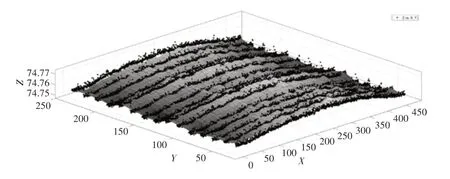
图8 圆柱度展开后的拟合平面Fig.8 Fitting Plane After Cylindricity Expansion
截面层数为15 层时,采样点分别为500、1000、2000、3000、5000时的三种方法的圆柱度误差测量结果,如表1所示。
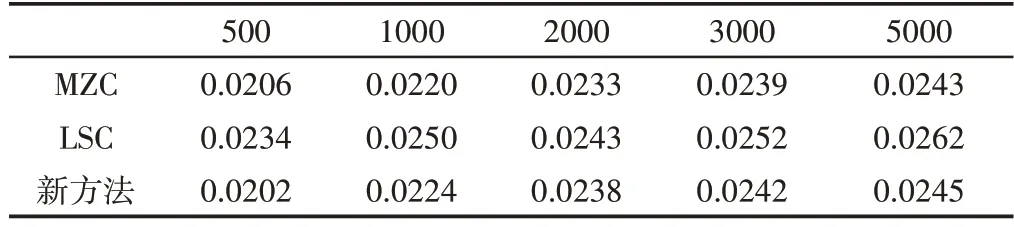
表1 不同采样点数圆柱度误差结果Tab.1 Results of Cylindricity Error for Different Sampling Points
f1、f2、f3分别代表当采样点数为1000时,截面层数分别为10,15,20时求得的圆柱度误差值,如表2所示。比较了在采样点数为1000,截面层数为15层时三种评定方法所用时间,如表3所示。
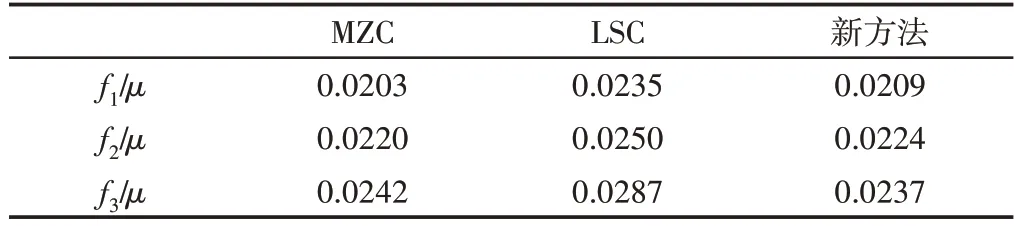
表2 不同采样点数求得圆柱度误差Tab.2 The Cylindricity Error Obtained by Different Sampling Points
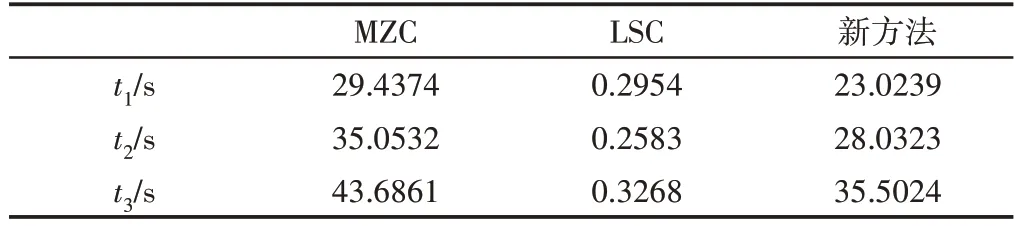
表3 不同采样点数圆柱度误差用时Tab.3 Time for Cylindricity Error of Different Sampling Points
对实验结果纵向对比,由表1和图9可知,当截面层数相同时,随着采样点数的增加三种方法测得的圆柱度误差也在提升。其中图9表示当截面层数为15,采样点数与圆柱度误差的关系。由表2可得,当采样点数相同时,随着截面层数的增加,三种方法测得的圆柱度误差的精度同样得到了提升。由表3可知,在采样点数和采样界面都相同的情况下,新方法用时相较MZC有着明显的提升。对于MZC和新方法,采取最小条件原则,随着截面层数的增多,拟合出的理想圆柱面越来越接近实际被测圆柱,所测得的圆柱度误差的精度在不断提升;同时由于二者都用到线性规划模型来求解误差,所求解矩阵维度增加,需要处理的数据点增多,用时t也随之增加。对于LSC,其实质是一种求近似的思想,不需要遵守最小条件原则,故随着截面层数的增加,精度并未受太大影响,计算速度也基本一致。
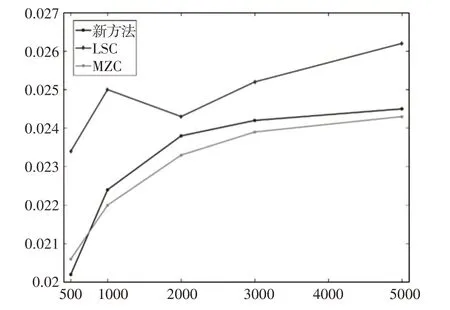
图9 采样点数与圆柱度误差的关系Fig.9 The Relationship Between the Number of Sampling Points and the Cylindricity Error
对实验结果进行横向对比,当采样点数为1000、截面层数为10层时,新方法与MZC相比误差值相差了3.04%,测量时间t提升了20.38%;采样点数不变,截面层数增至15层时,新方法与MZC的误差值相差2.53%,测量时间t提升了19.96%;截面层数增至20 层时新方法与MZC 的误差值相差1.92%,测量时间t提升了18.34%。由于不遵守最小条件原则,LSC相较于前两种方法误差精度相差较大。故在精度基本一致的情况下,新方法比MZC有着更快的计算速度。
5 结论
这里介绍了一种新的评价圆柱度的方法,在最小包容区域法的基础上运用降维的思想将三维圆柱度误差求解转化成二维平面度的求解。通过建立圆柱度降维求解的数学模型,沿拟合的最小二乘轴线将测量点转化为二维平面,得到了由测量点组成的平面模型,从而将三维圆柱度转化为二维平面度求解。由于都遵循最小条件原则,在精度基本一致的前提下,在最小包容区域法求解速度慢的问题上有所改善。通过实验验证了在不同采样点数和不同截面数下新方法的可行性,结果表明,在满足精度要求的前提下,评定时间均比最小包容区域法提升了约20%。
