车辆自适应巡航下的MPC方法的研究

何臣修，郭世永

（青岛理工大学机械与汽车工程学院，山东 青岛 266520）

1 前言

智能车辆（IV）和智能交通系统（ITS）是近年来的焦点话题［1］。它们集信息技术，传感器技术，自动控制技术于一体，为节省燃料消耗和减少污染物排放提供了巨大潜力［2］。车辆中配备的高级驾驶员辅助系统（ADAS）是ITS［3］的关键组件，通常包含自适应巡航控制（ACC），主动紧急制动（AEB），自动停车，换道辅助等［4］。作为ADAS的一项关键技术［5］，ACC可以通过执行控制系统来调节当前车辆的速度以实现车辆跟踪，它通常包括三个模块：感知，决策和控制［6］。感知模块可以通过轮速传感器和毫米雷达波获得当前和先前车辆的状态。然后，决策模块计算所需的加速度并将其传递给控制模块。控制模块操作制动或驱动系统以控制车辆的纵向运动。

关于ACC已有许多研究。恒定时间车距（CTH）和可变时间车距（VTH）［7］得到了广泛的研究。与只能解决简单工作条件的CTH相比，VTH的期望跟随距离随相对速度变化而变化。因此，VTH具有更好的适应性。然而，考虑到复杂的驾驶环境，VTH不涉及前车的加速，因此，还有更多的改进空间［8］。在ACC 流程中，并不是要唯一优化车辆动力学的目标。文献［9］提出了一种多目标解耦分层策略，并协调控制跟踪能力、燃油经济性和乘坐舒适性。除了这些方法，MPC还因为其有效性和最佳性能而成功应用于许多领域［10］。然而，沉重的计算负担对于数值优化是一个巨大的问题。在参考文献［11］中，提出了一种快速在线计算方法，以减少MPC控制器中后退水平优化的在线计算负担。

与以往的出版物不同，这里重点讨论了如何利用MPC来实现ACC的多个目标。

组织如下。第二节在模型预测控制（MPC）理论框架下对上层控制器进行综合。第三节提出了三种参数调整方法，包括高斯过程回归（GPR）和网格搜索（GS）。第四部分，在MPC 框架下，采用粒子群优化算法（PSO）进行优化。最后一部分，作者进行了总结。

2 跟车系统的建模

2.1 车辆纵向动力学的非线性补偿

由于发动机扭矩图是静态非线性的，随时间变化的齿轮位置和气动阻力作为车速的二次函数，因此车辆的纵向动力学是非线性的。传统的自适应巡航控制器包括两个层次，一个上层控制器和一个下层控制器。上层控制器根据车辆间状态和车辆状态确定期望的纵向加速度。下层控制器确定加速踏板位置和制动压力输入，以确保实际加速度跟踪所需的加速度。然而，在合成下层控制器时，纵向动力学模型的非线性存在带来了很大的挑战。为了弥补这一缺陷，应用了逆动力学控制设计方法［12］。期望加速度与实际加速度之间的关系可以表示如下：

式中：KL—系统增益；TL—时间常数。

通过频率响应法将参数识别为KL=0.99，TL=0.35KL

2.2 连续时间状态空间模型

根据车辆之间的纵向动力学，定义了两个状态变量。第一个是距离误差，表示为：

式中：ddes—驾驶员期望的车间距离，这里我们采用恒定时间间隔策略来描述：

式中：τh=3s—标称行车间隔时间，d0=15m是典型驾驶员的停车距离。第二个状态变量是速度误差，定义为：

式中：vp—前面车辆的速度；vf—后面跟随车辆的速度。

集成了广义车辆纵向动力学系统（GVLD）和车辆间纵向动力学系统，建立了汽车跟随系统的三状态空间模型，其模型如下：

其中，

式中：ap—前面车辆的加速度；u—控制输入；v—可测量的干扰；x—系统状态。

2.3 离散时间状态空间模型

考虑到MPC算法通常是在离散时域中设计和实现的，因此通过零阶保持（ZOH）离散化将连续时间转换为离散时间模型，得出：

式中：k—第k个采样点；A、B和G—系统矩阵，用数学表示为：

2.4 成本函数设计

跟踪能力通常根据速度误差和距离误差来指定，表示为：

油耗定义为所需纵向加速度及其导数的2范函数，而不是实际纵向加速度和加速度率：

然后成本函数可以表示为：

为了推导二次编程的标准形式，定义了以下向量：

因此，获得以下扩展状态空间模型：

其中，

QP问题的标准成本函数可以表示为：

其中，

2.5 MPC优化问题中的I/O约束

对于ACC中驾驶员的纵向乘坐舒适性问题，我们同时限制了加速度和加速度率，具体如下：

此外，采用驾驶员允许的跟踪范围标准来限制Δd和Δv并在特定范围内。

式中：Δdmin=-5m—Δd的下边界；Δdmax=6m—Δd的上边界；Δvmin=-1.0m/s—Δv下边界，而Δvmax=0.9 m/s是的Δv上边界。

MO-ACC算法的一个关键问题是预测优化问题的计算不可行性，这个QP问题可能没有最优解，因为硬约束永远不能满足。为了解决这个问题，我们引入了一个松弛变量来软化约束。

一个新的成本函数加上一个松弛变量的二次项可以表示为：

式中：ε—松弛变量；ρ—其加权系数。

当超过硬边界时，松弛变量将自动变为正值，以允许违反硬约束，从而避免潜在的计算不可行性。当硬约束不超过0时，就不会违反硬约束。

3 参数调整

MPC-ACC 问题的关键问题是参数的选择。影响结果的参数有Np，ωΔd，ωΔv，ωu，ωdu。在参数调整过程中，采用高斯过程回归和网格搜索的方法来寻找最佳参数。

3.1 评价指标TEI和FCM

跟踪性能的优度由TEI衡量（Δv和Δd使用标准单位）

式中：T—ACC的模拟时间（模拟中T=800s）；Δd—距离误差，单位为m；Δv—相对速度（m/s）。

后车燃油经济性用FCM（L/100km）衡量。

式中：S—跟车行驶距离，单位为km；

Qeng—发动机的燃油率，单位为L/s。

3.2 高斯过程回归（GPR）

首先，作者尝试使用高斯过程回归来调整其他参数，以获取函数的分布。在参数调整过程中，ωu和ωdu的最佳结果始终围绕以下数字（ωu=0.01，ωdu=0.01）。因此，GPR用于预测ωu和ωdu的最佳数。ωu和ωdu的结果，如图1、图2所示。

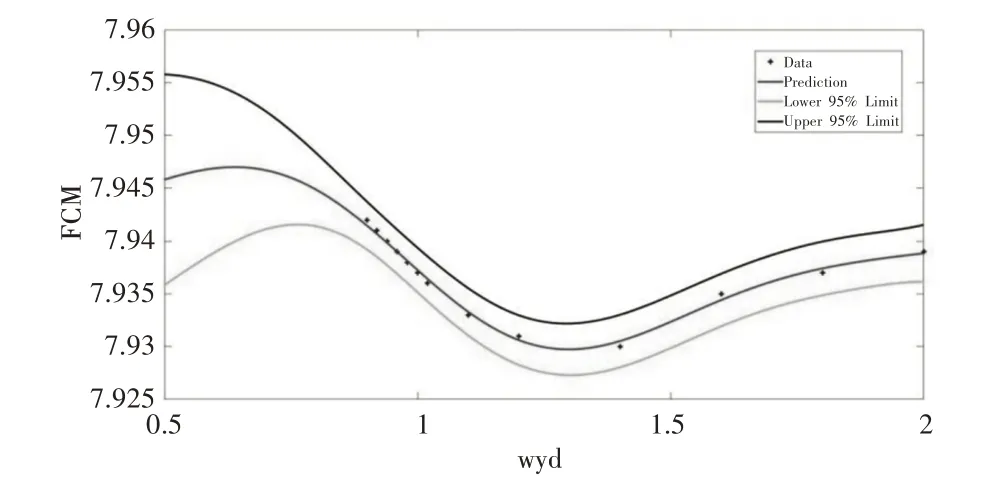
图1 FCM（GPR）的变化结果Fig.1 FCM（GPR）Change Results

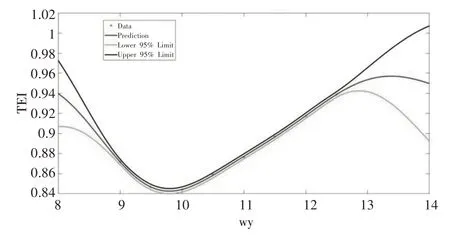
图2 TE（IGPR）的变化结果Fig.2 The Change of TE（IGPR）

当TEI和FCM达到最小值时，ωΔd和ωΔv的数量，如表1所示。

表1 参数Tab.1 Parameters

3.3 调整预测范围（Np）

在高斯进度回归之后，作者在更改“预测范围”的同时设置了其他参数，如表2所示。

表2 参数Tab.2 Parameters

反映TEI和FCM的结果，如图3、图4所示。

图3 FEI的结果Fig.3 Results of FEI

图4 FCM的结果Fig.4 Results of FCM

如图3、图4所示，当Np=4时，TEI和FCM的结果最佳。在这模拟中，当Np＞5时，Np越大，MPC的性能就越差。

3.4 网格搜索（GS）

但是，ωΔd和ωΔv的值将相互影响对方的最优值。为了更准确地获得最优参数集，采用了网格搜索（GS）。

GR的步长为0.01；

TEI、FCM的调整结果（GS）示意图，如图5、图6所示。

图5 TEI的调整结果（GS）Fig.5 Adjustment Results of TE（IGS）

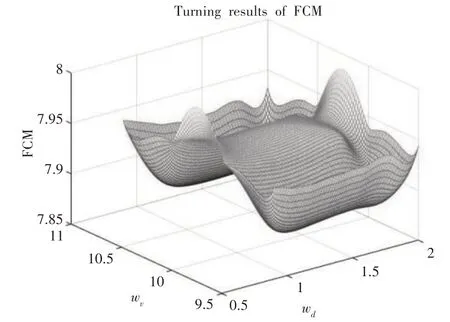
图6 FCM的调整结果（GS）Fig.6 FCM Adjustment Results（GS）

如图5、图6 所示，TEI 随着ωΔd的增加而减小，而FCM 随着ωΔv的增加而减小。最佳结果，如表3所示。第一行是GPR的结果，第二行是GS的结果。

表3 GPR与GS的最佳结果Tab.3 Best Results of GPR and GS

4 参数的自适应调整

4.1 参数的影响

第三节中提到的网格搜索方法提供了搜索更好的解决方案的方法。如果花费足够的时间，则会找到最佳解决方案。虽然通过上述方法搜索的解决方案是特定模型的最佳解决方案，但由于模型不匹配和错误，它可能不是ACC问题的最佳解决方案。

反映控制输出加速度的加权因子ωu对TEI的影响，如图7所示。在（0.01～0.1）范围内，ωu增大会导致TEI增大，这是因为加速度在0附近收缩，从而使车速状态恒定，当前一个车速变化时，速度误差和距离误差会导致TEI增大。

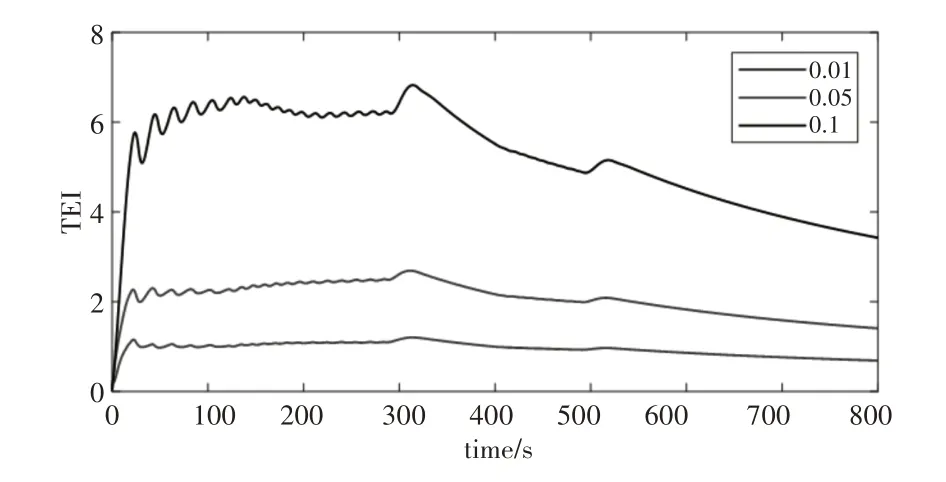
图7 ωu对TEI的影响Fig.7 Effect of ωu on TEI

反映ωu对燃油率的影响，如图8所示。在（0.01～0.1）之间，ωu增加。在总体趋势上会导致燃油率的上升，这意味着燃油率的成本函数不能完全代表燃油成本。在文献［13］中，恒定巡航速度不是燃油经济性的最佳策略，而脉冲和滑行策略使发动机工作在高效区，从而提供更好的燃油经济性。

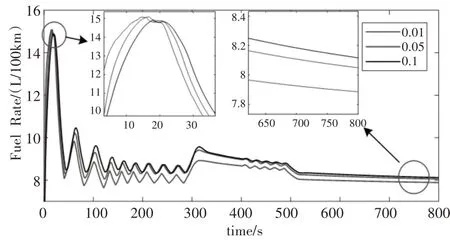
图8 ωu对燃料率的影响Fig.8 Effectofωuon Fuel Rate

因此，零加速不是燃油经济性的最佳选择。并且在不同的驾驶阶段，加速度的最优值是不同的，因此燃料成本的成本函数被改变为等式（1），其中，最佳加速度是根据驾驶阶段进行自适应调整的。

反映最佳加速度对TEI的影响，如图9所示。分别为0.5，5和0.01。范围在（-0.5～0.2）m/s2之间，ωu增加，将导致TEI的增加。

图9 最佳加速度对TEI的影响Fig.9 Effect of Optimum Acceleration on TEI

在总体趋势中，0m/s2和-0.5m/s2的aopt燃油经济性更好，并且其影响因巡航阶段而异。首先，-0.5m/s2的aopt更好，而下一阶段0m/s2更好。

4.2 参数的确定

根据A部分的结果和分析，提出了一种基于规则的参数变化方法，以提高燃油经济性。规则总结如下：（1）当远离所需距离时，增加距离的权重因子；（2）在远离所需距离时增加最佳加速度。反映不同误差参数的跟踪值，如表4所示。基于这组参数，TEI的跟踪性能为0.6338，FCM的跟踪性能为7892。

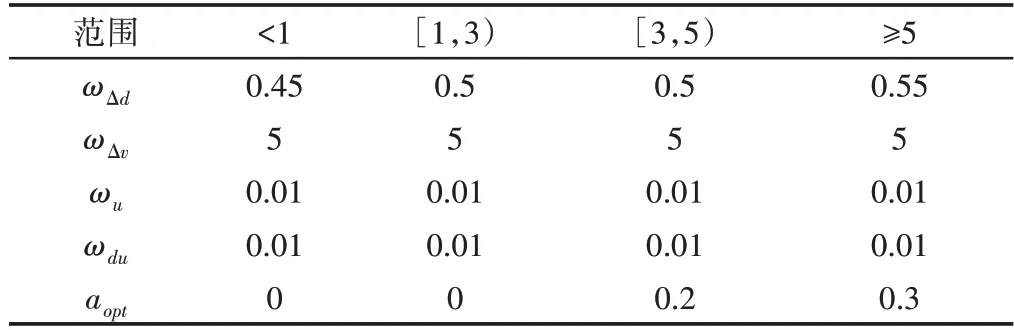
表4 不同误差范围内的参数Tab.4 Parameters in Different Error Ranges

5 粒子群优化算法

模型预测控制具有良好的动态控制性能，但计算量大等缺点更为明显。随着预测和控制域的增加，计算量也在增加，这可能导致控制器失去实时性。这里将粒子群优化算法应用于MPC问题的求解。在最优解基本一致的前提下，求解速度大大提高。

粒子群算法的思想来源于自然界鸟类群体的觅食行为［14］。其基本思想是初始化一组随机粒子，并对其在当前位置的适应度进行评估，从而得到每个粒子在当前位置的最优位置，即局部最优解。然后，程序比较所有的局部最优解，得到当前时刻的全局最优解以其他粒子的速度逼近全局最优解的位置。最后，确定当前结果是否满足要求，如果不满足，则需要重复上述过程，直到满足为止，并结束搜索。粒子群算法以其易于使用、全局寻优能力强、集变量少等优点而备受重视。方程（30）和方程（31）是算法的数学表达式，是代码的主要依据。

使用该算法求解MPC方程时，需要处理两点：（1）确定粒子与控制参数之间的关系，以及每个粒子的大小和粒子的搜索范围。（2）确定算法参数的值，包括最大迭代次数，粒子总数大小，加速度系数和惯性系数。以下讨论主要基于以上两点。

5.1 基于成本函数的PSO结构的构建

在MPC问题中，我们提到了成本函数，控制参数，预测范围，控制范围和约束条件等。在这里，我们将它们与粒子群算法相对应。成本函数的展开形式用作评估适用性的目标函数，控制参数为粒子。每个粒子具有四个维度，这是预测范围的大小。最后，MPC约束用于定义粒子群的搜索范围。这样，我们完成了算法结构的构建。

5.2 PSO参数的确定

这里将最大迭代次数设置为1000，如图10所示，图10（b）是图10（a）的局部放大图，具体显示了0到50次迭代期间最优值的下降趋势。可以看到，在第30代左右就已达到最佳解，随后的迭代不再重要，只会增加计算负担。

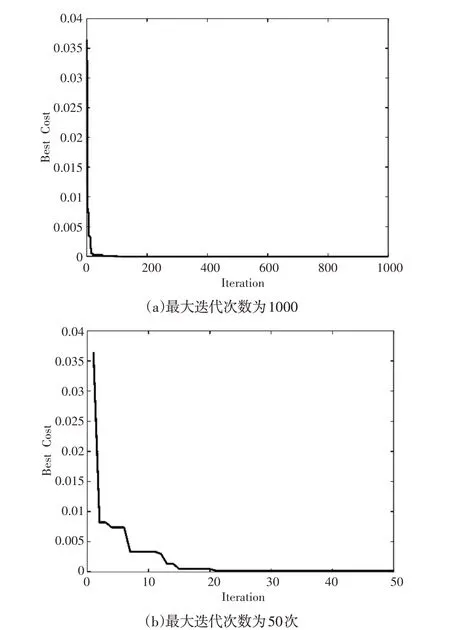
图10 最优值与迭代次数的关系Fig.10 Relationship Between Optimal Value and Iteration Times

然后进行了一系列的对比仿真。具体数据，如表5所示。综合考虑控制效果和计算时间，以最大迭代次数为10次为宜。这样，在保证最优解精度的同时，也提高了计算速度。

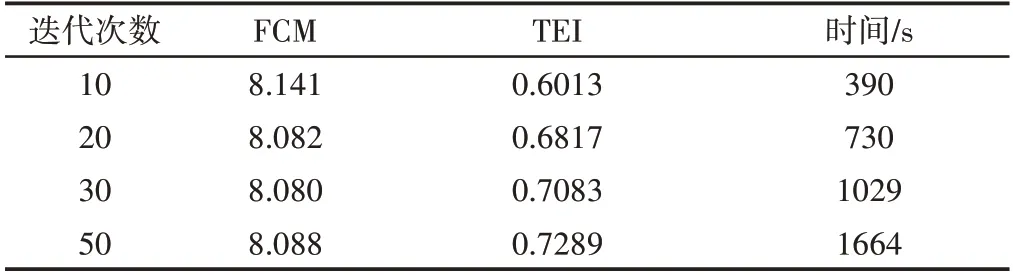
表5 对比实验数据Tab.5 Comparative Experimental Data

这里采用全局收缩因子来计算加速度系数，它可以控制粒子的动力学性能［15］。其数学表达式如下：

为了加快算法的收敛速度，这里采用线性变惯量系数［16］。公式是其计算方法，指当前迭代次数，w1及w2是惯性系数的初值和终值。整理后，w1=0.9，w2=0.4。这样，粒子群算法在保证最优解精度的同时，可以减少计算时间。

5.3 比较结果

最后，我们比较了常用内点法和PSO的结果。试验结果，如表6所示。根据指标及其计算时间，可以看出两者的性能基本相同。但是，PSO的时间大约是内部点方法的25%。验证了粒子群优化算法解决加速模型预测控制问题的可行性。

表6 效果比较Tab.6 Effect Comparison

6 结论

这里采用模型预测控制理论来同时满足有效跟踪能力，高燃油经济性，驾驶员期望响应和避免碰撞等控制目标，得出以下结论。（1）在ACC过程中，过多的跟踪误差可能会导致不可行的解决方案。使用约束管理方法纠正其优化问题后，MPC可以自动放宽约束范围，从而可以有效避免控制律的不可行解决方案。（2）在参数调整期间，使用高斯进度回归和网格搜索方法来找到权重ωΔd和ωΔv的最佳值。当预测范围NP等于4时，可以使用另一种参数自适应调整方法实时调整权重。（3）采用粒子群算法求解MPC 控制器的优化问题。在确保最优解一致的前提下，使用PSO优化目标函数可以大大提高求解速度。

由于MPC控制器具有较高的仿真性能，未来的工作将集中在实际车辆上。