水凝胶多场耦合计算力学

杨庆生, 刘 夏, 粘向川, 宗 婷, 乔海棣, 金 山, 唐爱杰

(北京工业大学 工程力学系,北京 100124)

1 引 言

水凝胶是一种由水和高分子聚合物组成的软体材料。水凝胶通常含水量较高,可以达到90%以上,具有类似生物组织的柔软性和弹性,具有良好的生物相容性。水凝胶的物理和化学性质可以通过调整高分子聚合物的种类和浓度以及交联度等进行调控,使其具有不同的凝胶性质和稳定性。作为一种功能性材料,水凝胶在生物医学、药物传递和环境领域有着广泛的应用潜力,其高水含量、生物相容性和可调控性使其成为研究和应用的热点。

近年来,水凝胶的研究主要聚焦于制备技术的发展和性能的改进。如双网络水凝胶可以有效地提高抗压强度、抗切割能力[1]和拉伸变形能力[2]。通过材料设计,发展了抗疲劳与低滞回[3]、高柔性[4]和高生物相容性[5]的水凝胶。

随着水凝胶的性能改善和日益广泛的应用,对水凝胶本构关系的研究迅速发展。如发展了水凝胶的热-电-化-力学耦合问题的一般理论框架和相应的有限元公式[6],实现了水凝胶化学-力学耦合有限元理论及其用户自定义单元(UEL)[7],用光-力耦合理论描述有限变形连续介质热力学框架内光异构化水凝胶的光-力学响应[8],考虑链缠结效应的热响应水凝胶本构模型[9],以及纤维增强水凝胶的各向异性本构关系和有限元计算方法[10]等。最新的学术专著总结了水凝胶力学的研究进展[11,12]。

基于水凝胶材料,人们设计了各种结构与器件,在生物医学和柔性电子器件上具有广泛应用前景。如通过一种多尺度的设计方法制备了具有高拉伸性、高抗疲劳性、低滞后和稳定传感能力的离子导电复合水凝胶,可将其用作生物医学柔性应变传感器[13];在剪纸结构的设计基础上,结合水凝胶的力学和传感性能,设计了多裂纹、大变形和高灵敏传感器,可用于机器人的控制[14]。关于水凝胶结构设计的研究进展评述参见文献[15]。

水凝胶结构不仅具有复杂的几何形状,而且伴随着水凝胶自身热-化-力学耦合作用,这些复杂结构和耦合问题一般难以直接解析计算,因此发展水凝胶及其结构的多场耦合计算力学是十分必要的。水凝胶多场耦合计算力学是基于多场耦合本构理论,实现水凝胶结构分析的重要手段。除了传统的基于物理原理的数值方法,如有限元法之外,基于数据驱动的机器学习方法对水凝胶及其复合材料进行力学性能预测与微结构设计正在逐渐展开[16]。

本文主要聚焦于水凝胶的多场耦合计算力学,发展基于水凝胶耦合本构理论的计算力学方法,在微观和宏观尺度上对水凝胶材料和结构的多场耦合力学行为进行数值模拟。

2 基于粗粒化分子动力学的水凝胶微观计算力学

水凝胶由水和聚合物网络组成,其中聚合物网络的微观结构是保证其具备所需性能的基础。由于聚合物分子链的规模巨大,全原子的分子动力学(MD)模型计算成本很高,因此本文发展了水凝胶的粗粒化分子动力学(CGMD)模型。CGMD在模拟介观尺度结构的同时保留了体系的分子特性,同时借助深度学习的数据拟合能力,建立双网络水凝胶CGMD模型中力场函数,对不同聚合物网络微观结构的力学性能进行数值模拟。

2.1 双网络水凝胶的多尺度模型

双网络水凝胶以聚2-丙烯酰胺-2-甲基丙烷磺酸(PAMPS)为第一网络、聚丙烯酰胺为第二网络(PAAm),亚甲基双丙烯酰胺(MBAA)为交联剂,第一网络聚合物链短且交联浓度高,第二网络聚合物链长且交联浓度低,如图1(a)所示。构建的双网络水凝胶全原子模型如图1(b) 所示。

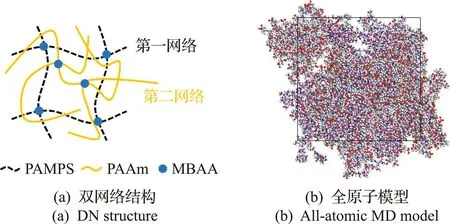
图1 双网络水凝胶聚合物网络结构

建立无定型聚合物混合体系之后,使用半径搜索法进行交联反应。模型在一定温度下,当两个交联位点处的原子距离在设定的最大交联半径内,两个原子之间形成共价键,完成一次交联。每隔一定的时间步统计交联浓度,直到达到设定交联浓度时,完成交联反应,否则继续扩大最大交联半径交联,在每次交联成功后进行两次退火操作,使模型均匀混合,充分交联,两层网络均匀混合,互相缠绕,没有空洞。

双网络水凝胶模型的原子间相互作用由一致价力场描述,电荷分配采用电荷平衡法,静电相互作用的计算使用粒子网格法。模型体系的三个方向均采用周期性边界条件,以消除可能的边界影响。使用能量最小化方法优化初始构型,将系统的能量降至最低。

全原子MD模拟结果如图2(a)所示,单向拉伸结果包含弹性阶段、屈服阶段、颈缩阶段与应变硬化阶段,结合对拉伸过程中微观结构的观察,全原子模型的MD拉伸模拟表现出与实验一致的双网络水凝胶能量耗散性质与拉伸趋势,证明了构建的双网络水凝胶全原子MD模型的合理性。

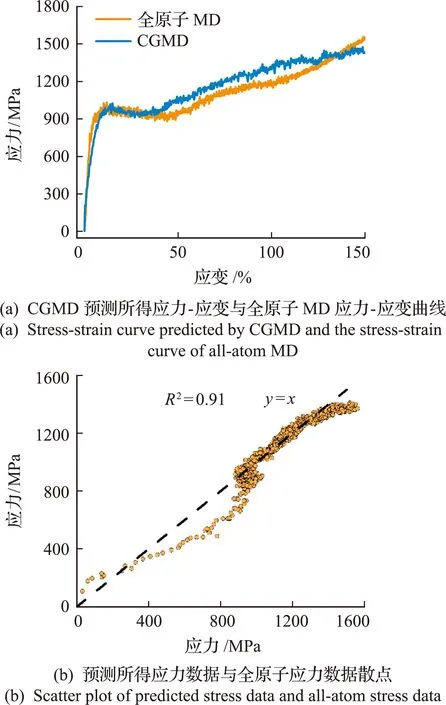
图2 神经网络模型预测结果

为了进一步缩减计算规模,本文建立了CGMD。建立CGMD模型包含两个步骤,即确定映射规则与粗粒化力场。映射规则中,映射比越大,每个粗粒子包含的原子越多,损失的原子内部微观结构精度越大。不同的映射规则对应不同的粗粒化力场。CGMD模拟需要选用合适的力场参数,以贴近真实的模拟结果。现将PAMPS/PAAm双网络水凝胶体系划分为5种粗粒子,如图3所示,因此有6种键类型。

图3 粗粒化映射规则

用LJ势描述不同类型粗粒子之间的非键相互作用,

(1)

用有限伸展非线性弹性势描述键合相互作用,

4εF[(σF/rij)12-(σF/rij)6]

(2)

式中rij为第i和第j粒子之间的距离,rc为截止距离,εLJ和εF为非键合与键合粗粒子之间相互作用强度,具有能量单位。σLJ和σF为非键合与键合粗粒子之间的平衡距离,具有长度单位。R0为最大键长,K为刚度系数。当同一聚合物链上的键合粗粒子距离小于R0时,式(2)的第一项表示粒子的相互作用力,当键合粗粒子的距离大于R0时,式(2)的第二项表示粒子的相互作用力。

使用不同的力场参数,可以得到相应的拉伸力学性能。将力场参数在给定的范围内随机取值[22],并将粗粒化模型充分弛豫,进行与全原子MD模型相同的拉伸过程,得到CGMD模型的应力-应变数据。

2.2 深度学习预测粗粒化模型力场参数

经过批量的CGMD模拟,得到5000个样本,将数据集随机分为训练集、验证集和测试集。使用MD模拟得到的应力数据存在小幅度的数据振荡,在不降低数据精度的前提下,使用Savitzky-golay 滤波器对应力数据进行平滑处理。为了消除量纲差异和避免奇异样本数据造成影响,使用最大最小标准化的方法归一化处理数据。

将预处理数据输入神经网络,随着迭代次数的增加,损失函数越来越小。通过不断优化超参数,损失函数达到预期目标,随着迭代次数的增加,训练集和验证集的误差和损失值都趋于平稳。此时,各层的权值与偏置使得神经网络的预测值最接近真实数据,从而得到训练完成的神经网络。将测试集用于训练完成的神经网络,测试其预测性能,证明了训练的神经网络模型具有良好的预测性能与泛化能力。

将双网络水凝胶全原子MD模型进行拉伸之后的应力数据作为目标力学性能,输入到训练好的神经网络模型中,即可预测得到目标力学性能下的双网络水凝胶CGMD模型力场参数。如图2(a)所示,将预测所得的粗粒化力场参数进行MD模拟得到的应力-应变数据与目标力学性能的进行对比,图2(b)展示了预测所得应力数据与目标性能的应力数据散点图,在拉伸的弹性阶段,曲线拟合有较小误差,其他阶段的误差在可接受范围内。

综上所述,双网络水凝胶的多尺度MD模型提供训练数据,深度学习方法提供模型参数,可为底层规则清晰而变量复杂的粗粒化力场求解提供思路。建立双网络水凝胶的CGMD模型,使得在更大的空间尺度和时间尺度上模拟水凝胶材料变成可能。

3 基于唯象本构理论的多场耦合计算力学

3.1 水凝胶的多场耦合计算力学

水凝胶在热-化-力等多种因素耦合作用下,展现出丰富的驱动变形模式,研究其多场耦合问题一直是一项富有挑战的课题。

此外,从水凝胶本身考虑,其聚合物链上一般存在不同官能度的交联点和链缠结效应,为此Yang等[17]考虑上述因素构建了一种自由能函数,本文对上述自由能函数做了进一步发展[9]。将发展后的自由能函数用于研究水凝胶的溶胀和拉伸行为,其具体形式为[9]

(3)

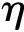
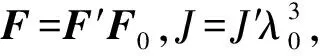
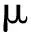
(4)

最后,本文解析了不考虑链缠结效应水凝胶在离子浓度为0的溶剂中达到平衡,并沿方向1受到单轴拉伸时的变形和力学响应。变形状态可以通过给定的纵向拉伸λ1和两个横向拉伸λ2,λ3来表征,其中λ2,λ3可由λ1和这两个横向的名义应力方程为0求得。名义应力s1可由给定的纵向拉伸λ1和求得的λ2和λ3代入方向1的名义应力方程后求得。不同的λ1和求得的λ2和λ3如图6(a)所示,因为是单轴拉伸,所以λ2=λ3,单轴拉伸时,

图4 不考虑链缠结效应时水凝胶的初始溶胀

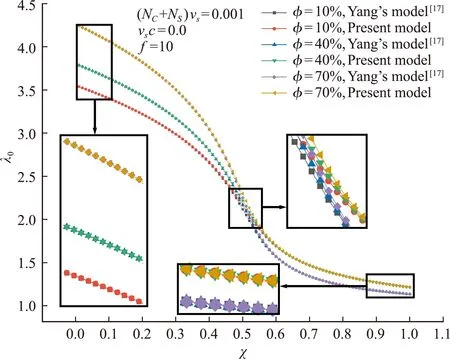
图5 考虑链缠结效应时水凝胶的初始溶胀

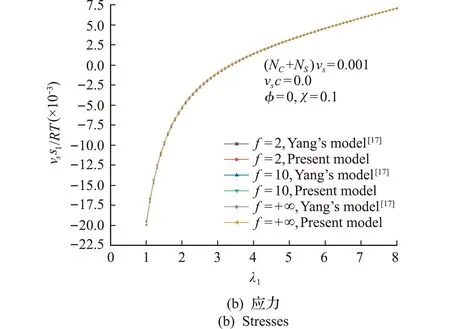
图6 不考虑链缠结效应时水凝胶的单轴拉伸行为

3.2 纤维增强水凝胶计算力学

受自然界生物组织的启发,在水凝胶基质中添加纤维是有效提高水凝胶力学性能的方法之一。为建立纤维增强水凝胶的力学模型,本文利用以下基本形式构建总自由能函数,

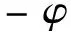
(5)

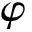
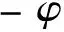
(6)

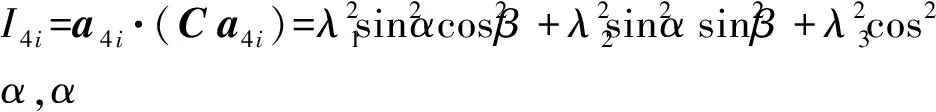
(7)

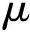
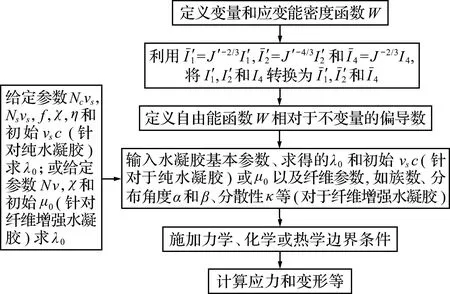
图7 水凝胶多场耦合的计算流程

图8 纤维在三维空间中的分布[10]

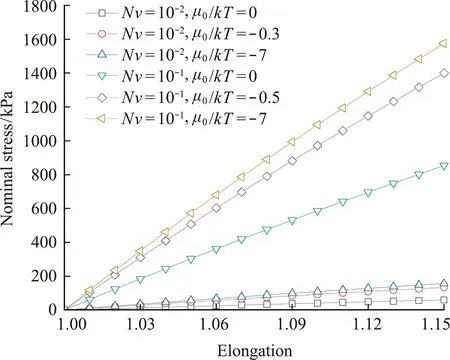
图9 两种代表性Nv在不同溶胀状态下的拉伸行为

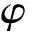
表1 溶胀模拟使用的材料参数

表2 拉伸模拟使用的材料参数

图10 不同f时的溶胀行为

图11 不同f时的拉伸行为

4 基于水凝胶智柔结构的多场耦合计算力学

4.1 水凝胶双电层电容式传感器

利用离子水凝胶设计一种双电层超级电容器,如图12所示。金属极板上的电子层和离子水凝胶与极板接触面积处的离子层构成了大容量的双电层电容。

通过设计不同形式的微结构可以提升传感器的灵敏度,微结构的存在使介电层(离子水凝胶)响应更快和更易变形,在降低载荷的同时,也降低了电容初值。在加载过程中,随着极板间距离减小,极板与离子凝胶介电层上的微结构接触面积逐渐增大,相应正负极极板上的异号离子电荷随之增多,实现在较小载荷加压的工况下有较大的电容量的变化,从而提升传感器的灵敏度。灵敏度计算为

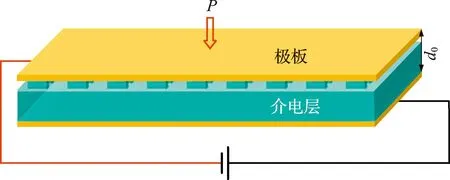
图12 平行板电容器

(8)

式中C为电容,C0为电容初值,ε0为真空介电常数,εr为介电体相对介电常数,A为极板正对面积,d为极板间距,S为灵敏度,P为压力。

常用的电容式介电体微结构形式主要有规则形结构,如圆柱形、金字塔形、棱台形、圆锥形和半球形等;非规则形结构,如仿指纹状、仿玫瑰花状和层状丝结构等,如图13所示。

图13 介电体微结构

应用有限元仿真进行介电体材料的非线性变形仿真模拟,并将变形结果导入HyperMesh中进行网格实体转换处理,将处理的变形实体结果导入COMSOL多物理场耦合软件中,进一步分析得出微结构形变后的电容值,基于灵敏度计算公式得到具有不同微结构介电体的灵敏度。为保证初始电容值的相对一致,各种微结构的初始总体积和高度值保持相近。仿真模拟结果如图14所示。

通过多个软件的耦合应用,最终获得具有介电层微结构的超级电容器的非线性力-电响应结果。半球形微结构灵敏度计算仿真流程方法,可以为构

图14 半球微结构仿真结果

造具有更高灵敏度响应的复杂非规则介电层微结构提供设计方案。

4.2 基于水凝胶的超结构设计与计算

水凝胶材料的模量相对较低,可产生较大的变形。将水凝胶智能材料和超结构的设计思想结合起来,可创造既具有特殊力学性能,又具有主动感知和智能响应的力学超结构。通过合理设计其微结构和组成材料,可以实现特定场景下的功能。本节基于文献[20,21],介绍基于水凝胶材料进行超结构设计和计算的思想,从而确定智能材料-微结构-力学性能之间的耦合关系[20]。

将内凹结构的设计方法与复合梁在水溶液中定向弯曲的变形原理相结合,可设计水凝胶驱动的负膨胀智柔超结构[20]。

超结构因其具有和声子晶体一样的晶格周期性排布的特点,为带隙的形成提供了条件。水凝胶智能超结构由于其具有大变形的特点,可以用来调节弹性波的传播,不同的应变状态具有不同的带隙分布。

以上利用水凝胶材料吸水膨胀的特性设计并制备了一种负膨胀智柔超结构,开发了多材料结构分析的多场耦合有限元法。利用水凝胶作为驱动材料的智能结构设计,赋予了传统结构新的功能特性,使其具有了可编程、可调控和自驱动的能力。

利用水凝胶的溶胀变形,结合双材料复合梁和剪纸结构设计,可以将这种溶胀转换为弯曲变形,可以实现更为复杂的膨胀变形模式,如正/负膨胀、各向同性/各向异性和弯曲变形,为设计多模式变形行为的超结构创造了范例[21]。

将双层复合梁引入星结构,并获得一个结构-功能集成的智能星结构,其在溶液中可以实现自主和可控的负膨胀异常行为。根据所需的复合梁数量,设计了三星单元、四星单元和六星单元[21],如图17所示。图17显示了二维超结构的膨胀变形。该结构可以进一步发展为三维超结构,具有形状可控和互逆变换等特点。

图15 水凝胶与弹性结构的组合超结构[20]

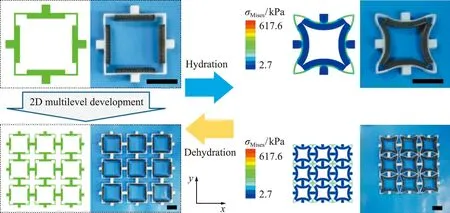
图16 二维负膨胀超结构晶格[20]

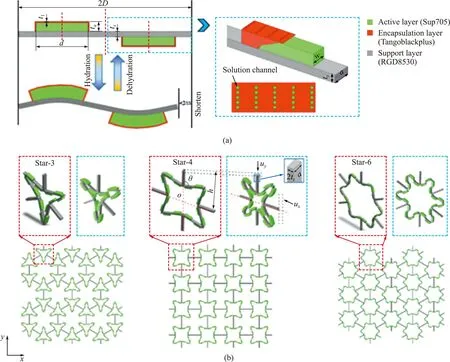
图17 星形软力学超结构设计策略[21]

5 结 论

在微观尺度上,本文提出了聚合物交联网络的粗粒化分子动力学(CGMD)方法,利用深度学习得到了粗粒化力场参数,为水凝胶的微观计算提供了有效的数值方法。在此基础上,研究了两层交联网络占比、链长以及交联浓度等对双网络水凝胶力学性能的影响;在宏观尺度上,在化-力耦合本构理论的基础上,提出了各向同性水凝胶与各向异性复合凝胶的耦合有限元法,可用于分析和设计各种复杂形状和复杂性能的水凝胶结构。

水凝胶多场耦合计算力学是为了满足分析水凝胶这类多场耦合、非线性大变形材料与结构的力学行为而提出来的。基于CGMD方法和多场耦合本构理论,设计相应的算法和程序,进行水凝胶的宏微观力学性能计算,是水凝胶结构分析与设计的主要手段。

后记：本文为祝贺钟万勰院士九十华诞曁《计算力学学报》创刊四十周年而作。钟先生长期倡导与引领计算力学的发展,并为此做出了巨大贡献。在本文准备过程中,钟先生不幸仙逝,谨以此文缅怀追忆先生。